Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

Да… Европейцы столкнулись с проблемой неравномерной темперации строя в связи с оргáнами. Любопытно, что вначале они тоже пошли по «китайскому пути», пытаясь вычислить высоты полутонов. И тоже пришли к десяти одинаковым полутонам и двум отличающимся по высоте, но тоже равным.

Этими вычислениями занимался немецкий математик и теоретик музыки Генрих Граммáтеус (1492-1525гг.). Он повторил китайцев в расчёте полутонов.

Следующий шаг совершил итальянский теоретик музыки и композитор Винченцо Галилеи (1520-1591гг.), отец знаменитого астронома Галилео Галилея.

Из статьи о нём в Википедии: «В настройке лютни он предлагал делить октаву одинаковыми полутонами 18:17 – эта величина, хотя и рассчитанная приблизительно, весьма близка равномерно темперированному полутону.»

Зачем нужны были р а в н ы е отношения между звуками, зачем нужна была одинаковая м е р а отношений между их высотами (один и тот же коэффициент) и почему именно оргáн потребовал этого?

Тысячи труб – это тысячи звуков.

Это – невероятные возможности проявления мощи звучания.

Это – великий соблазн создать грандиозную модель грандиозного мира: Вселенная-Земля-Человек с его душой и духом. Соблазн смоделировать такую сложную Жизнь, в которой, тем не менее, всё как-то согласуется, – причём в к а ж д ы й м о м е н т существования мира.

Вот если бы в мысленном эксперименте «Жизнь» мы в какое-то мгновенье нажали клавишу «стоп» (как на компьютере во время кинофильма), мы бы увидели о д н о в р е м е н н о е сочетание всех движений всех существ и явлений, попавших в «кадр», – словно замерли, зафиксировались отдельные ноты мелодий их жизней (в масштабе Вселенной – жизней планет, звёзд, галактик…). Мы бы увидели что-то, похожее на аккорд.

Мы бы увидели, что в каких-то точках все сложные движения согласуются, не мешают друг другу и даже вторят друг другу, – и тем поддерживают друг друга. Они оказались в моменте к о н с о н а н с а. Они словно упорядочивают множество всех, таких разных, движений, – которые кажутся нам на первый взгляд сплошным хаосом.

В хаосе есть точки, которые и не согласовываются друг с другом – диссонансы. Они рассеяны, не согласованы друг с другом. В них нет силы. Сила проявляется в согласованности.

Сила аккорда – в согласованности его звуков-точек, в г а р м о н и и.

Мир не рассыпается в пыль хаоса благодаря консонансам.

Слова «точка» и «точный» – родственники.

Чем точнее консонансы – тем большей силой они обладают.

Фиксированные звуки флейт, ставших трубами оргáна, и желание самогó пространства-времени, желание самой Жизни явить себя в аккордах – совпали.

Каждый звук должен был иметь шанс поучаствовать в аккорде: ведь все они рождены квинтой-доминантой. Шансы у всех звуков должны были быть р а в н ы. Один и тот же коэффициент отношений между звуками устанавливал это равенство.

Так и явилась в мир музыкальных звуков идея р а в н о м е р н о й

т е м п е р а ц и и всего музыкального строя.

Как ни странно, задачку с этой самой равномерной темперацией (причём, точнее всех) решил человек, на родине которого и не помышляли об оргáне. Соотечественников этого гения вовсе даже и не интересовали его эксперименты и расчёты. Заинтересовали только 200 лет спустя.

Чжу Цзай-юй.

Нам уже встречалось это имя.

Он был современником Винченцо Галилея ( Винченцо Галилей: 1520-1591гг., Чжу Цзай-юй: 1536-1610гг.).

Так в одном информационном поле Земли о д н о в р е м е н н о вспыхнули импульсы-озарения Мысли европейской и китайской. Им оставалось только окончательно слиться в консонансе.

Но кто такой Чжу Цзай-юй?

– Учёный, астроном, математик, лингвист и музыковед, изобретатель музыкальной темперации.

Так представляет его нам Энциклопедия.

Интернет может более обстоятельно познакомить тебя с его биографией – если, конечно, возникнет к этому интерес.

А ещё он был человеком сильного духа.

Когда его отца, принца по рождению, жившего во дворце, оклеветал завистливый родственник, возжелавший занять высокое положение при императорском дворе, в результате чего отец оказался в тюрьме, 14-летний Чжу Цзай-юй ушёл из дворца и поселился в землянке. Не впасть в уныние ему помогла страстная любовь к наукам, – чем он и занялся в своём уединении.

Оргáн он, естественно, не мог построить в своей землянке. Но в его распоряжении были флейты и струнный инструмент цитра.

Древнюю китайскую «Систему 12 люй» (для флейт) он изучил очень досконально. С пифагоровой системой (для струн) наверняка тоже был знаком. (Китай давно установил торговые отношения со странами Средиземноморья через Шёлковый путь, а потом – морской.) Оставалось сравнить эти две системы, найти в них то общее, что их объединяет, и… привести их к консонансу.

А общим у этих систем было их астрономическое и математическое происхождение. Только подход к природе звука отличался. У флейт – звук-точка, у струн – звук-волна.

(С подобной двойственностью столкнулись европейские учёные-физики 16-18 веков, когда изучали природу света. Англичанин Исаак Ньютон остался приверженцем корпускулярной теории: свет (фотон) – есть частица-корпускула («точка»), правда, со свойствами волны. Англичанин Томас Юнг доказал, что свет – волна, и даже измерил длины световых волн. А вместе получилась корпускулярно-волновая теория.)

Чжу Цзай-юй создавал «флейтово-струнную» теорию музыкального строя (тоже в своём роде корпускулярно-волновую (не в строгом смысле, конечно, а по подобию), – для звуков).

Пифагорову комму он решил р а в н о м е р н о распределить на все 12 люй (до их повторения на новом витке), а по сути – на 12 квинт (ведь все люй образуются квинтами) и точно зафиксировать полученные высоты звуков. Для этого ему надо было точно рассчитать длины флейтовых труб, – с учётом распределённой между ними коммы.

Это примерно то же, что 365 земных суток разместить в 360 (365˚ в 360˚).

Спираль замкнуть в кольцо, – как мы ощущаем время земного года: всегда с возвратом в одну и ту же точку (Новый год).

Солнечно-лунная пифагорова комма равномерно «растеклась» по 12-ти квинтам (как по 12-ти месяцам земного года). Квинты зазвучали в соответствии с числом

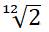
Чжу Цзай-юй нашёл своих очень заинтересованных сторонников не в родном Китае, а в далёкой Европе.

Там над темперацией трудились знаменитые математики – голландец Симон Стевин и француз Марен Мерсенн. Они всё ещё искали свои варианты, как и композитор Андреас Веркмейстер, вдохновлявший И.-С. Баха. Но всё-таки равномерно темперированный строй Чжу Цзац-юя одержал верх. Наверное, из-за своей универсальности. Этот строй стал международным.

…Ты же помнишь, что мы начали эту тетрадь с темы эволюции – то есть «развёртывания» жизни.

Равномерно темперированный строй и стал именно р а з в ё р т ы в а н и е м.

Развёртыванием чего? – Да октавы же!

И тоже – по подобию.

Вот Пифагор с в е р н у л октаву, чтобы получить м и к р о -звуки, виновница которых – комма. Он показал, что подобия уводят в микро-мир, мир тонких материй и энергий, в мир волн и колебаний.

А темперированный строй показал иное подобие. Подобие в сторону увеличения.

Ступень обычной октавы развернулась величиной в саму октаву и, прошагав семь шагов-октав (подобно семи ступеням гаммы-гептатоники), стала величиной в клавиатуру. (Можешь проверить на своей клавиатуре.)

Каждый полутон обычной октавы стал подобием квинты этой же октавы. И 12 этих квинт уместились в семи октавах, – как 12 хроматических ступеней в гамме.

В общем, твоя клавиатура – это огромное подобие октавы (гамма + «хвостик» из оставшихся звуков).

Если к клавиатуре-октаве прибавить ещё одну, и ещё одну, и ещё… – доберёмся до вселенских масштабов!.. Это же мечта оргáна!

Клавиатуры оргáнных мануалов отдают дань особого почтения квинте, этой прародительнице жизни: количество октав каждого мануала – 5, как правило. Но мануалы некоторых оргáнов могут иметь и 5, и 7 октав, – выражая почтение и квинте, и гептатонике (гамме). Музыкальный строй ведь содержит и то и другое.

Если учесть ещё и педаль (ножную клавиатуру) в две октавы с «хвостиком», то в особо величественном оргáне всего октав наберётся от 33 до 37.

То есть, космическому замыслу пифагорова строя оргáн дал развёрнутый – просто гигантский! – масштаб. Представляешь, – каждому из 36-ти звуков и микро-звуков – разворот величиной в целую октаву!

А как же это космическое круженье, которое так прекрасно моделировала струнная кифара? Доступно ли его передать жёстким флейтам-трубам?

О, как изощрённы бывают модуляции человеческой Мысли!

Разрастаясь («развёртываясь»), оргáн покинул поля, где властвовал Пан. Тысячи труб нуждались в особо экономной «упаковке» (как природа экономно «упаковывает» атомы в молекулах и кристаллических решётках сложных образований – веществ, клеток…).

Вариантов этих «упаковок» столько, сколько и самих оргáнов (ты видел на картинках). Они стали архитектурными «организмами». И, как и любой организм, они нуждались в защитной оболочке.

Самой подходящей защитой оказались храмы.

У слова «храм» столько смысловых модуляций – ой-ой-ой!

Самый простой смысл – «дом», наша охрана в жизни. Да и само слово звучит очень близко к «хран» – охрана.

Вариант этого слова – «хорóмы», от «хорóм». Вот в этом варианте появляется смысл «хор» и его модуляция – «гор», гора. Хор – это общность множества голосов, приведённых к согласованности, гармонии:

согласованность человеческих мелодий жизни, а в более широком смысле – жизней всех «тварей» («творений»), населяющих Вселенную. «Гор», «гора» – высота, взлёт, кульминация, доминанта жизни, высшее проявление её сил.

В английском варианте храм – temple. В этом слове намёк на Время в вариациях его быстроты: пространство-время разных скоростей жизни разных творений Вселенной – во взаимной согласованности.

Какие музыкальные смыслы!

Геометрический смысл – куб и сфера: куб самого тела храма, а на сферичность указывает купол. (В проекции на плоскости – это квадрат и круг, и, может быть, намёк на бесконечность известной нам «квадратуры круга». А может быть, «прямоугольное круженье»…)

Вселенная из звуков, помещённая в эту охранную оболочку, стала вести себя в соответствии с моделью настоящей вселенной. Круженье вернулось. Как? – Во многом благодаря полусфере купола.

Звук любит полёт. Звуковые волны охотнее всего взлетают в высоту (всем известно, что звук от источника внизу лучше прослушивается вверху, а не на уровне источника). А вверху – сферическая поверхность купола. Вот и завихриваются о т р а ж е н и я звуковых потоков, и обволакивают нас. И может закружиться голова – как от звуков кифары.

А ещё палитра звуков оргáна развёртывает себя в ТЕМБРАХ.

Слово тембр происходит от франц. timbre, от греч. timbanon (timpanon) – «ударять». В теории звука означает «качество звука». А качество (характер) звука зависит от призвуков, обертонов, сопровождающих основной звук. А особенности призвуков зависят от ф о р м ы колебаний источника звука. А эта форма колебаний зависит от качеств материала, из которого сделан источник звука (шероховатая или гладкая форма, жёсткая или мягкая…).

Трубы оргáна сделаны из дерева и металла: одни – из дерева, другие – из металла. У деревянных труб – тембр мягкий, бархатистый, глубокий, обволакивающий. У металлических труб – тембр жёсткий, гладкий, пронзительный. Однако, металл подбирается для труб мягкий: сплав олова и свинца – чтобы звуки, обладая силой металла, не резали при этом слух.

Просто неизмеримое количество звуков может творить оргáн – и впрямь хватит на все творения Вселенной.

Слушая оргáн в храме (или концертном зале с хорошо рассчитанными отражательными свойствами – как в храме), мы оказываемся посреди круженья.

Тональности, шагая по квинтам вверх и вниз, тоже кружат.

Всё – как в космосе.

Само пространство-время кружит в музыке. И всё изобилие звуков (с их обертонами и отражениями) , которое может сотворять оргáн, представало бы хаосом, если бы не закон консонансов – совпадений, согласований, созвучий: гармонии.

Чем больше звуков, тем больше они нуждаются в организации – гармонизации, тем сильнее должна проявлять себя власть гармонии.

Вот эту силу и власть гармонии и дал АККОРД!

Аккорд непременно должен был родиться. Настало его время.

Вот если бы мы могли у в и д е т ь круженье звуков, круженье звуковых волн, когда звучит орган под куполом храма…

Мы бы у в и д е л и, как возникают моменты согласования между какими-то звуками среди многих, и это согласие объединяет и усиливает мощь этих звуков. Если бы мы остановили такой момент, чтоб у в и д е т ь…

Знаешь, в книге К.Пиковера «Великая математика» меня поразила одна картинка, невероятно похожая на такой момент. Странная Сфера Александера…

Она вся – словно из вдруг явившихся взору и замерших витков многочисленных спиралей потоков (воздуха? звуков?).

Это именно м а т е м а т и ч е с к и й объект, созданный американским математиком Джеймсом Александером. И этот объект называется с ф е р о й, потому что обладает важным геометрическим свойством сферы – непрерывностью. Он п о д о б е н сфере. ( В книге употреблено выражение «гомеоморфен сфере»: греч. homoios – «подобный», morphe – «форма». То есть, этот объект и сфера – п о д о б н ы е формы по свойству непрерывности.)

Этот объект, если приглядишься, бесконечно воспроизводит п о д о б и я самого себя. А ведь это – принцип и музыкального строя!

Вначале на картинке не очень понятно, чтó происходит, кáк всё это организуется. И вдруг… Начинаешь видеть точки (узлы), которые находятся в согласовании друг с другом!

Сферу моделируют смыкающиеся-размыкающиеся пальцы – большой и указательный.

То, что мы увидели, математиками называется ф р а к т а л о м.

Фрактал – родственник Золотого сечения.

Поразительный момент: формат самóй книжной картинки позволили измерить «аккорд» обыкновенной линейкой. И линейка показала при этом числовые меры Ряда Фибоначчи…

Ещё одной интересной особенностью представшего нам объекта является то, что кольца витков р а з о м к н у т ы (пример с пальцами, приводимый К.Пиковером в статье к картинке) – как в случае с витками спирали: каждый виток спирали – разомкнутое кольцо. И очередное подобие фигуры образуется в месте размыкания. Такое явление нам уже встречалось:

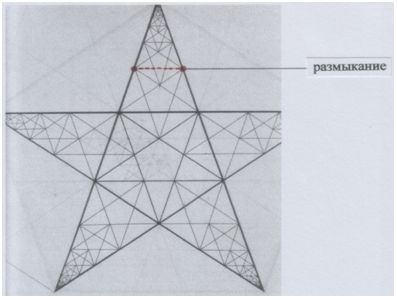
Рис. и пометки автора.

Как непохожи все эти фигуры: Сфера Александера, обыкновенная сфера, пентаграмма. А музыку вообще невозможно у в и д е т ь.

Но все эти явления родственны, п о д о б н ы, потому что сам принцип их организации – с а м о п о д о б и е.

И аккорды тоже рождены в мир этим принципом.

Если изобразить звуковые пространственные волны на плоскости (как мы привыкли их себе представлять), то среди множества волн совпадающие по одной линии гребни-кульминации и явят нам аккорд.

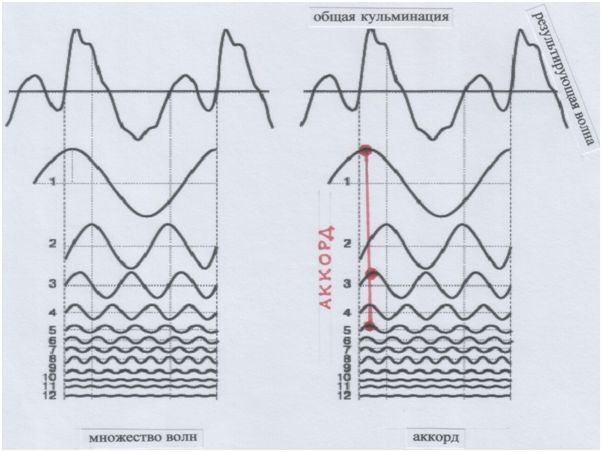
Рис. и пометки автора.

Наше умозрение аккорд видит как в е р т и к а л ь посреди звуковых потоков. Аккорд упорядочивает эти потоки силой своей вертикали. Он – сила. В музыкальном пространстве-времени он совпадает с сильной долей.

В музыке архитектуры он предстаёт колонной. И тогда он подобен древнегреческому Атланту, который весь порядок небесных сфер держит на своих плечах.

Если подумать о природе и о Древе Жизни, аккорд – ствол этого Древа.

Корень Древа подобен глубокому гулкому басу, основанию. Волнующаяся листва кроны – мелодии…

Бас – сокровище оргáна. Его гул похож на бездну и на незримый, но весомый и плотный, центр гравитации. Никакой иной музыкальный инструмент не владеет этим сокровищем – не по силам! Великан один лишь может…

Реликтовое излучение – бас Вселенной. Центры галактик, их опоры – бас. Он – первый тон в основании ТОНАЛЬНОСТИ (какие бы образы эта «актриса» ни принимала). В мире космического круженья он тоже подчиняется закону квинт-доминант. Только поступь его облечена особым Величием.

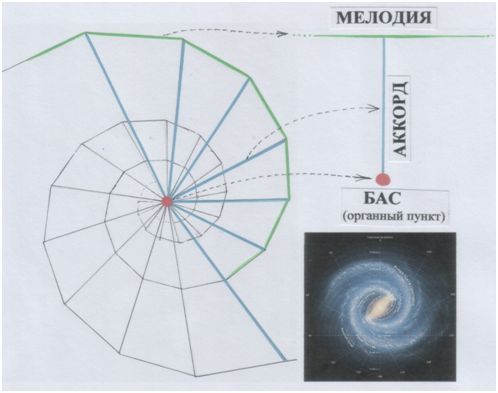
Рис. и пометки автора.

БАС – АККОРД – МЕЛОДИЯ.

Вот триада, моделирующая пространство-время в звуках.

Науки и искусства изобретают свои особенные термины для феноменов (явлений) мира, в которых про/являются его законы.

На первый взгляд ( или слух) термины запутанны, как хаос, непонятны, а потому скучны. Пока не проникнешь в их живое сердце…

Вот, например, такой «запутанный», сложный, многословный термин:

«ГОМОФОННО – ГАРМОНИЧЕСКИЙ СКЛАД».

…Но ведь у нас с тобой уже есть опыт проникновения в самое сердце терминов зрением ума.

«СКЛАД» – это понятно: складывать – прилаживать что-то друг к другу, прикладывать, упорядочивать – порядок.

«ГАРМОНИЧЕСКИЙ» – от «гармония»: консонансы, согласованность; в концентрированном проявлении – аккорд.

«ГОМОФОННЫЙ»…

Здесь нам и понадобится применить опыт проникновения зрением ума. В сердце, в корень. Вернее, в корни этого слова.

Греч. phone –«звук».

Лат. homo – «человек». Греч. homos – «равный», «взаимный», «общий».

Вместе – «человеческий звук»: голос, мелодия. Звук, общий человеческому голосу и своей собственной природе – непрерывной волне.

В переводе на более понятный музыкальный язык мы получим в результате: «МЕЛОДИКО – АККОРДОВЫЙ ПОРЯДОК (СТРОЙ)».

Вот когда употребляют термин «гомофонно-гармонический склад», то имеют в виду эту стройную триаду: БАС – АККОРД – МЕЛОДИЯ.

Это – о б о б щ ё н н а я модель мира в звуках.

Обобщённая – значит, без подробностей, без определённых мер, – в отличие от подробно рассчитанной октавы. Но при всём при этом геометрия даёт нам возможность увидеть, что обе эти модели – п о д о б н ы.

Только обобщённая модель, как и любое обобщение, выглядит величественнее.

Величие оргáна и востребовало утверждения такой грандиозной обобщённой модели. А р а в н о м е р н а я т е м п е р а ц и я посодействовала её созданию.

Бас – это центр гравитации (подобный центру галактики на наших картинках). Он утверждает себя как ТОНИКА – фундаментальный ТОН, фундамент, основание ТОНАЛЬНОСТИ – на какую бы квинту он ни взошёл.

Вместе с собою он переносит и модуль ОКТАВУ, внутри которой и рождается очередная ТОНАЛЬНОСТЬ со всеми своими АККОРДАМИ и МЕЛОДИЯМИ.

Бас тоже кружит по квинтам. Так центр нашей галактики (вместе с самóю галактикой) летит по какой-то гигантской спирали – к созвездию Геркулеса.

И тональности-времена жизни, возникающие на этом великом пути квинт, изменяются, м о д у л и р у ю т, обновляются.

И сама наша, человеческая, МЫСЛЬ кружит во Вселенной в соответствии с этой грандиозной моделью, – открывая ф у н д а м е н т а л ь н ы е законы мира (например, фундаментальные законы физики нашего мира), своды-аккорды законов в разделах наук (на примере физики – законы поведения твёрдых тел, жидкостей, газов, света, атомных и субатомных частиц и т.д.) и «мелодии» – линии развития этих наук во времени.

Аккорды в музыке – это моменты-импульсы совпадения, согласования нескольких импульсов (сильных проявлений) вращающихся звуков. Эти совпадения предстают перед нами как вертикаль, выстроившаяся в момент, когда мы этому вращению сказали «стоп» (мысленный такой эксперимент). В такой момент мы можем обнаружить, что звуки аккордов тоже вращаются. Иначе говорят, что они о б р а щ а ю т с я.

Тогда триада-трезвучие предстаёт перед нами в новых своих образах. Слово «обращение» соединяет в себе два смысла: «вращение» и «образ». Как ТОНАЛЬНОСТЬ является нам в образах разных (различающихся) тональностей, так и АККОРД – в разных образах. – Принцип подобия!

Чтобы увидеть этот сказочный процесс (в сказках ведь персонажи всё время обращаются в кого-то другого, – оставаясь при этом собою), воспользуемся ключами понимания – клавишами.

Итак, – образы-обращения триады (трезвучия):

Рис. и пометки автора.

А может ли быть т р е т ь е обращение?

Клавиши показывают, что – да. Конечно, – да.

И оно возвращает нас к начальному трезвучию, но на новом витке, в новой октаве.

Это подобно тому, как начальный звук-прима превращается в октавный звук, образуя интервал ОКТАВУ. Октавный звук повторяет приму на новом витке спирали восхождения. Он – словно отражение примы.

Трезвучие повторяет себя своим третьим обращением – по принципу образования этого октавного звука – и получает своё отражение в новой октаве.

И всё повторяется снова и снова – до бесконечности. Лишь бы хватило клавиатуры…

Вот и само слово «повторение» – от «второй». Два. Характеристики октавного звука: 2 – частота волны, ½ – длина волны.

Третье обращение повторяет начало. «3» и «2» неразделимы в явлении вращения. Взаимоотношения «3» и «2» указывают на квинту: 3/2 – частота волны, 2/3 – длина; 5-я ступень в гамме и октаве (3+2). Трезвучие вписывается в квинту внутри октавы, само же своими хроматическими звуками повторяет октаву (смотри комментарии к картинке со Сферой Александера). Как всё взаимосвязано! …Потому что – п о д о б н о.

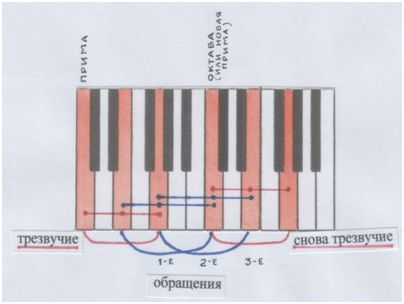
Рис. автора.

Рис. автора.

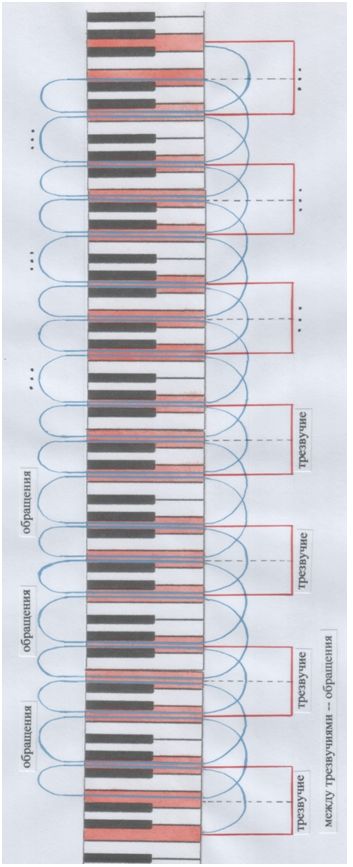
Рис. автора.

Ключи и печати. (Нотация как специфическая геометрия.)

Авторский коллаж на основе рисунков из Интернет источников в свободном доступе. В центре – картина Р.Делоне «Бесконечные ритмы»

…Мысль летуча.

…Звук летуч.

Ключи знают тайну, но хранят молчание.

Мысль облачается в звук. Ключи открывают вход-выход. Мысль звучит и …исчезает. Неуловима. Кто узнает о ней, когда смолкнут звуки?

ЗаПЕЧАТлеть! – Отражение, тень, оттиск – портрет на память. Печать мгновения.

Кто з н а е т тайну печатей, тот открывает их, – и развёртываются свитки Мысли, вновь облачаясь в звуки.

Пожалуй, тебе известно, что NOTA имеет смысл «знак».

Откуда слово nota? – Предполагают, что из старинного слова gnata, которое связано глубоким родством со словом gnoscere – «знать».

«Знать» – это, конечно же, не просто получать информацию (иначе превратишься в кладовку, где хранятся случайные неупорядоченные вещицы). Настоящее знание вырастает из п о н и м а н и я и в н и м а н и я.

Внимать в себя, сопоставлять с тем, что уже внял до; сравнивать, упорядочивать, организовывать; находить родство, связи, аналогии. Подобия…

Клавиатура-«ключница» явила нам великий фундаментальный Закон квинт.

Как он заПЕЧАТлел себя в нотной записи – думаю, ты догадываешься, ибо он и здесь проявил свою фундаментальность:

Рис. автора.

Стан! – На нём весь храм музыки держится, как на фундаменте. Стан – стал.

На нём всё время происходит с т а н о в л е н и е гармоний-аккордов, мелодий. Вся их изменчивость – на фундаменте порядка.

Как он протяжён! Бесконечен, как музыка всех времён.

Чем он ещё любопытен? Допускает ли он случайности-вольности, – например, в пространственном расположении своих пятилинейных полос?

Давай проверим? Поэкспериментируем?

Рис. автора.

Итак, верхняя полоса – для квинт вверх, нижняя – для квинт вниз.

А между…

Пространство для ещё одной – подразумеваемой, невидимой – квинты.

Размыкание.