Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

Все эти числа связаны с круженьем.

Тысячелетней давности задачка о квадратуре круга тоже оказалась связанной с бесконечностью и в результате – неразрешимой.

Но зато она в конце концов привела к очень даже современной идее

ф р а к т а л ь н о й г е о м е т р и и. А идея всё та же: ломать прямую на подобные кусочки-отрезки бесконечно и измерять их, измерять, измерять… Эти вычисления стали возможны только в век компьютеров.

Во все времена человеку хочется постичь и смоделировать мир, в котором он рождён.

У Пифагора не было компьютера. Но ему тоже хотелось моделировать.

Вот что он подметил проницательно, так это то, что звук своей природой, своей физикой воспроизводит законы формирования космического пространства-времени. И создал не компьютерную, а звуковую модель этого пространства-времени!

Он создал модуль мира-космоса – октаву.

А звуки сами воссоздают круженье: они ведь – волны!

И модулируют – по подобию.

Интересно, что египтяне (древний Египет), пытаясь решить проблему квадратуры круга, тоже не избежали увлечения идеей музыкальности. В формулу площади круга они включали очень даже музыкальную дробь.

Сравни: Площадь круга диаметра d считалась равной площади квадрата со стороной 8/9d.

Рис. автора.

Обратный ход – к прямоугольности. Прямоугольные волны в современной радиотехнике: волны-меандры.

Меа́ндр (по названию геометрического орнамента в виде ломаной линии) – периодический сигнал прямоугольной формы, широко используемый в радиотехнике и электронике. Длительность импульса и длительность паузы между импульсами в одном периоде такого сигнала равны.

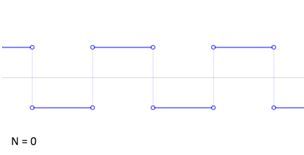
Рис. автора.

(Если пожелаешь посмотреть анимацию о том, как образуются такие волны, набери в поисковике «меандр значение слова», выбери «меандр – вид импульсного сигнала».)

Смешение времён!

А Пифагор бессмертен.

Октава всё ещё жива.

Музыка всё ещё моделирует пространство-время.

Но что же было с музыкой после Пифагора?

ЧТО БЫЛО ДАЛЬШЕ?

Ключи. (Эволюция музыки как эволюция жизни. Оргáн. Флейтовая теория. Рождение темперированного строя и клавиатуры.)

Жизнь.

Жизнь была дальше.

И музыка-жизнь.

В жизни – эволюция.

Эволюция – это перемены, и з м е н е н и я форм вещей и существ. То же, что м о д у л я ц и и (ты же помнишь, что модуляция – это закономерное

и з м е н е н и е).

Маленькие клеточки-точки объединяются во всё более сложные формы.

Если интересно, – Энциклопедия всегда готова прояснить любую мысль:

Эволюция – от лат. evolutio – «развёртывание», закономерное изменение.

Развёртывание – это укрупнение: малое превращается (модулирует) в большее, но в соответствии с общими и для малого и для большого законами.

Изменения в космосе, изменения на Земле.

Простенькие атомы водорода «развернулись» в сложную Таблицу Менделеева. Космическая пыль – в галактики. Клеточки жизни – в homo sapiens (человека разумного).

Маленькие государства-города древней Греции (полисы) «развёртывались» в империи (империя Александра Македонского, затем – Римская империя).

Силы множественных греческих богов «развернулись» в мощь единого Бога, Всемогущего.

Музыка жаждала мощи, силы, величины. Или Величия.

Струна – тонка. Она нежно ударяет по воздуху, и тот долетает до нашего слуха подобно ласкающему ветерку. Звук лёгкий, изысканный,– для тонкого душевного (психейного) внутреннего нашего мира. Очень личный голос.

Личность, её душа, её отдельная мелодия – вот что может выразить струна.

А множество мелодий могут ли, объединившись,«развернуться» в единую мощь? Даже множество струн выразят ли её?

Пространство-время, изменяясь, искало для выражения себя новый голос.

Хор. Множество голосов, усиливающих друг друга. Не соло души, а мощный единый дух.

И… труба!

И… аккорд!

Вот что было нужно.

Отвергнутая когда-то Афиной флейта Пана требовала своего возрождения. Она желала возродиться вновь, но уже в новом обличье.

Греческое слово pan означает «всё». Греческий Пан был богом, который подчиняет себе множественность: бог пастухов и их стад; бог лесов со всем многообразием населяющих их существ. Его флейта имела силу подчинять своим звукам множество жизней, объединять их силы в единую мощь.

Афина же отдавала предпочтение героям-личностям, личному человеческому духу и миру души. Она отдала предпочтение струнной кифаре.

Но пришло время флейт.

Звук флейты пронзителен и прям. Воздух, сжимаясь в её трубе, вылетает подобно стреле или снаряду и ударяет по нашим барабанным перепонкам напрямую (не опосредованно, как от колебаний струны).

Струна растягивается и сжимается, колеблется; звук кружится и растекается волнами. Флейта непоколебима. Жестка и прямолинейна. Её длину и диаметр не изменишь в процессе игры. Раз отрезал – и всё.

Флейта требовала фиксации звуковых высот, их точности – в соответствии с точным расчётом своих параметров. Её отверстия для регуляции воздушного потока должны точно соответствовать определённым высотам звуков (да и сами они похожи на точки).

Энциклопедия:

Фиксация – от лат. fixus – «закреплённый».

Греки отличались пытливым умом и изобретательностью.

Они явили миру инструмент, который можно было бы назвать «суперфлейтой» (гиперфлейтой) Пана.

Гидравлос!

Изобретатель – древнегреческий математик и механик Ктесибий.

Это такая водяная флейта, или водяной орган.

Вот тебе и эволюция – «развёртывание» идеи флейты до масштабов органа!

Более подробная информация – на следующей странице.

Источник – Википедия

Гидравлос – довольно сложное механическое сооружение. Оно именно

м е х а н и ч е с к о е. Управлять звуком непосредственно (как к струнам – непосредственно прикасаясь чуткими пальцами) на нём просто невозможно.

Разве можно было на нём передать всё богатство звуковых красок пифагорова строя (36 звуков-оттенков!)?

Звуковые оттенки, которые давали микрооктавные интервалы в пифагоровой октаве, наверняка пришлось упростить.

Но зато появилась сила звучания. Эта сила – сильнее человеческого голоса.

Сила нашего голоса зависит от силы наших лёгких, от их мощности.

С помощью наших лёгких мы можем надуть воздушный шарик. А велосипедную шину, к примеру?

Насос куда мощнее наших лёгких!

В гидравлосе был применён насос.

Богатство звуковых оттенков было принесено в жертву силе звучания. Этой силы должно было хватать на покорение слуха сотен и тысяч собиравшихся вместе слушателей.

Как музыканты управлялись с гидравлосом? – Так сразу не поверишь: ударом кулака! И колотили они по специальным дощечкам шириной 5-7 см, устроенным на горизонтальной панели. Вот эти дощечки и получили название: К Л А В И Ш И.

Откуда взялось это слово – КЛАВИША?

– От латинского слова clavis – «КЛЮЧ».

Почему «КЛЮЧ»?

Да потому что ключ открывает и закрывает вход-выход.

В случае с гидравлосом клавиши были связаны с клапанами, которые открывали и закрывали вход-выход для воздушного потока в трубах.

Стукнул по нужной клавише – и полетели волны воздушного давления к нашим ушам, чтобы наш мозг превратил их в звук.

Разные трубы – разные волны – разные звуки.

Вот можешь полюбоваться на первую клавиатуру:

На этой клавиатуре ещё нет знакомых нам чёрных клавиш. Все клавиши – одинаковы. Что бы это значило?

(Очень жаль, что на фото греческого гидравлоса не видно клавиатуры. Но орган из древнего города Аквинкум в бывшей провинции Римской империи – на территории современной Венгрии – наследует сам принцип устроения греческого инструмента.)

Почему все клавиши одинаковы?

На какой музыкальный строй они намекают?

На этом инструменте 13 клавиш (посчитай сам). На греческом – 24.

По-видимому, нам опять придётся прогуляться на Восток – к вавилонянам, шумерам и… в Китай. К вавилонянам и шумерам прогуливался и Пифагор, и другие его соотечественники. А вот Китай…

Каким-то образом шумерская и вавилонская цивилизации пересекались в древности с китайской цивилизацией – ещё более древней, чем шумерская. Кто у кого заимствовал всяческие премудрости – до сих пор остаётся загадкой: то ли китайцы учились у шумеров, то ли шумеры – у китайцев… Но известно, что в Китае существовала очень-очень древняя музыкальная система, разработанная для… флейт! И кем? –Опять же – а с т р о н о м а м и!

Эта система называлась «Система 12 люй».

(Если пожелаешь познакомиться с этой системой обстоятельно, знай, что есть такой сайт http://synologia.ru Музыкальная теория.)

Так вот, иероглиф люй буквально означает «правило», «устав». В музыке – это система звуковысотных эталонов (так написано в статье на сайте). То есть система из образцов высоты каждого звука – эталонов этих звуков.

Страницей ниже (так, на всякий случай) – отрывок из статьи.

Всё очень просто. Как у шумеров и египтян. Пространство-время планеты Земля в космосе измеряется вращением по окружности: 360 «шагов» (градусов) – 360 дней года; год – из 12-ти месяцев. Каждому месяцу соответствует звук определённой высоты. Образуются звуки в соответствии с лестницей квинт (тебе это знакомо по пифагоровому строю). Только эта лестница поделена на одинаковые ступени, по половине тона. Каждому звуку – по ступеньке: 12 звуков – 12 ступеней. По-нашему это будет так:

I ступень – ДО VII ступень – ФА диез

II ступень – ДО диез VIII ступень – СОЛЬ

III ступень – РЕ IX ступень – СОЛЬ диез

IV ступень – РЕ диез X ступень – ЛЯ

V ступень – МИ XI ступень – СИ бемоль

VI ступень – ФА XII ступень – СИ

Как китайцы получили эти звуки?

– Из квинт! Опять-таки из квинт.

Ну что поделать, если квинты – это доминанты, то есть высшее проявление силы, а значит, и выразительности (или выраженности) каких-то явлений – энергии, волны, например: гребень волны, её кульминация, импульс. А весь мир – из волн (как мы уже понимаем).

Эти доминантовые кульминации (импульсы) показаны в фильме «Вселенная. Звуки космоса» из нашей первой тетради. Они представлены как звуки новорождённой Вселенной, которым больше 13 миллиардов лет. Это происходит на в о с ь м о й минуте фильма. Ты ведь можешь пересмотреть этот фрагмент.

С этих доминантовых импульсов и началось то, что я в и л о с ь, с т а л о б ы т ь, то есть сам мир, сама жизнь.

Посмотри на ленту из квинт с привычными названиями нот ( не умею писать иероглифы, а ты не умеешь их читать):

Рис. и пометки автора.

Здесь все необходимые звуки для всех 12-ти ступеней.

Они окажутся рядом, если мы свернём эту ленту спиралью и учтём, что не закрашенные карандашом ноты – это подобия тех вертикалей ступеней, которые мы получали в строе Пифагора: то есть мы будем шагать через одну квинту, и постепенно у нас выстроится весь ХРОМАТИЧЕСКИЙ китайский звукоряд.

(Эту спираль найдёшь на следующей странице.)

Так что выходит, что ХРОМАТИЧЕСКИЙ звукоряд – родом из Китая.

Хроматический – значит, построенный по полутонам.

Однако само название «хроматический» – от греческого слова chromatos –«цвет», «окраска».

Греки вообще мыслили звуки цветными: семь звуков гаммы (гептатоники) подобны семи цветам радуги. А каждый полутоновый звук подобен оттенку: ФА – цвет, ФА диез – оттенок ФА… и т.д.

По-гречески, весь звукоряд состоял бы из лимм.

Модели автора

В случае с флейтами такой звукоряд был очень удобен. Трубы есть трубы, чем проще – тем лучше.

Конечно, и в таком звукоряде есть октава. Стóит лишь добавить 13-ю ступень, подобную первой ступени, но на новом витке.

Дело только в том, что китайцы не мыслили и н т е р в а л а м и – отрезками, в которые вписываются звуковые волны, не мыслили звуки в о т н о ш е н и и друг к другу, – то есть никакого принципа относительности.

Тем более удивительно, что их строй оказался совместим с пифагоровой октавой.

А может, и НЕ удивительно: ведь оба строя сотворены из одних и тех же «атомов» – квинт.

Зачем трубам относительность? Фиксированный звук (зафиксированная, эталонная его высота) – вот и всё, что нужно трубам. Фиксированный размер трубы – фиксированный звук.

Для гидравлоса, первого оргáна – первого духового механического инструмента – такой строй вполне подходил.

Слово оргáн – тоже греческого происхождения (греки изобрели, греки и назвали). Происходит оно от слова οργανον (органон) – «орудие», «инструмент», «машина».

Вот что сообщает Энциклопедия по поводу оргáна:

Оргáн – крупный музыкальный духовой х р о м а т и ч е с к и й клавишный инструмент с мехами, трубами для извлечения звука.

Вот! Х р о м а т и ч е с к и й инструмент. Вот почему количество клавиш первых оргáнов – в соответствии с хроматическим строем. Вот почему все клавиши – одинаковы, «равны». Как равны полутоны.

Однако не всё было так просто с этим хроматическим строем, как кажется на первый взгляд.

Мы-то знаем теперь, что звуковые волны ведут себя в соответствии с астрономическими особенностями поведения Земли в космосе, между Солнцем и Луной. Пространство-время Земли задаёт её годовой поворот не в 360˚, а в 365˚ (или 366˚). Поделить этот поворот (виток спирали на самом деле) на р а в н ы е 12 частей не получается. А значит, какие-то из этих частей не будут подчиняться равенству, и 13-й полутон не повторит в точности первый ( а это – звук октавы). Потому Пифагор и ввёл к о м м у, микроинтервал-разницу.

Китайцы просто две части из двенадцати чуть изменяли. На слух это было не очень заметно. Ведь духовые инструменты предназначались для игры на открытом воздухе, где воздушные волны быстро рассеиваются, и уши не успевают разницу уловить. Тем более, если исполнять только м е л о д и и – п о с л е д о в а т е л ь н ы е звуки.

Первые оргáны ( те самые гидравлосы с небольшим количеством труб) тоже использовались для больших праздников на открытом воздухе.

Оргáны покоряли Европу. Сила их звучания очень даже соответствовала имперскому духу (Римская империя), духу Величия.

Да, оргáн – это е в р о п е й с к и й инструмент. И китайские хроматизмы-полутоны постепенно вживились в древнегреческий строй (Греция ведь – Европа), в пифагорову октаву. Для этого пришлось пожертвовать микроинтервалами.

Та клавиатура, которую мы знаем, и демонстрирует нам этот процесс вживления полутонов-хроматизмов в октаву Пифагора.

Пифагорову октаву взялись представлять собой белые клавиши, среди которых сохранились два естественных полутона: МИ-ФА, СИ-ДО.

Мы можем проследить этот процесс образования нового строя. Его показывают клавиши. А клавиши, мы теперь знаем, это – КЛЮЧИ. Ключи, которые открывают путь не только потокам воздуха и волнам звука, но и волнам МЫСЛИ, понимания.

Это ты увидишь на странице ниже.

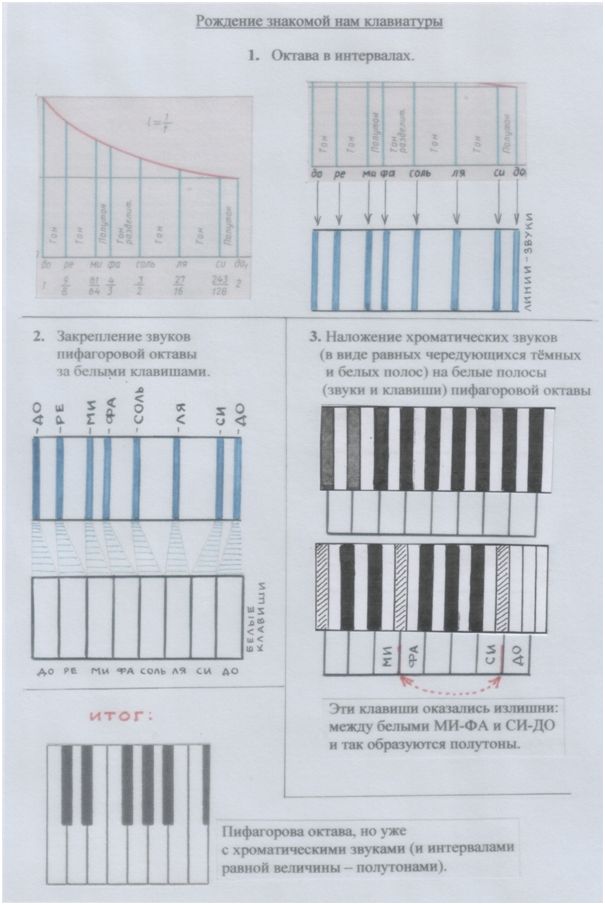
Рис. и пометки автора

Благодаря клавишам-ключам октаву теперь можно было не только услышать, но и у в и д е т ь. Ещё её можно было о с я з а т ь, прикасаться к ней.

Сам порядок мира (такой неуловимый, незримый) можно было «взять в руки», исследовать его, испытывать его свойства – и на слух, и на взгляд, и на ощупь одновременно. Играя клавишами-ключами, мир можно было

м о д е л и р о в а т ь, создавая бессчётное число моделей жизни (которые впоследствии стали называться пьесами, этюдами, сонатами и т.д. – муз. произведениями).

«Китайский след» в европейской октаве (изначально – пифагоровой) ты можешь увидеть, услышать и осязать, постукивая своими молоточками-пальцами по чёрным клавишам. Ты услышишь китайские наигрыши. Ты услышишь п е н т а т о н и к у («пента» – «пять», «тон» – «звук»). Играя ключами чёрных клавиш, ты можешь моделировать какие-то «наброски», мелодии жизни «по-китайски» (как будто на китайском языке).

Устойчивое отношение «3» и «2» (тернарность и бинарность, троичность и двоичность) навсегда впечаталось в клавиатуру:

Рис. и пометки автора.

И это всё – след КВИНТЫ.

О т н о ш е н и е трёх к двум и двух к трём – след пифагорова «струнного» подхода, волнового подхода: частоты и длины в о л н. И – и н т е р в а л ы.

С у м м а ( последовательное присоединение фиксированный значений):

3+2=5 – квинта в виде зафиксированных звуков-ступеней ( квинта ведь – пятая ступень в октаве). «Флейтовый» подход, сущность которого – зафиксированная высота звука.

Геометрический символ этого – пентаграмма, которая была священна и в древнейшей китайской культуре, и священна для Ордена пифагорейцев.

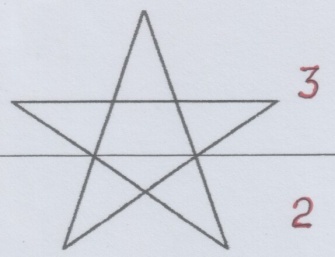
Рис. и пометки автора.

(Интересно, что разгадать загадку устойчивости сочетаний «3» и «2» не получается (до сих пор!) даже у современной физики.

В поисках самой малой частицы мироздания – на субатомном уровне – физики добрались до к в а р к о в. И выяснилось, что получить о д и н кварк невозможно. Они связаны какими-то гиперсильными силами в пары или тройки. И чем большую силу прилагают, чтобы разъединить эти пары и тройки, тем крепче кварки сцепливаются друг с другом !

А числа, которыми описывают свойства кварков, словно позаимствованы из музыкального строя.)

Какие же невероятные возможности открывал оргáн для музыки, для моделирования жизни из волн (волн звука)!

Флейт (труб) можно было использовать любое количество.

Количество струн ограничено небольшими размерами рамы самой лиры (или арфы). А трубами можно уставить хоть стадион! Лишь бы клавиатуры хватило.

И что же стало?

Оргáн превратился в архитектурное сооружение!

Архитектурное сооружение из тысяч труб (бывших флейт).

3 тысячи, 4 тысячи. …33тысячи труб!

Самый гигантский и самый мощный по силе звука оргáн был построен в 1929-1932г.г. в Америке, в Атлантик-Сити (штат Нью-Джерси). 33 112 труб!

Вот это развёртывание идеи оргáна! Даже за пределы Европы, через Атлантику. И за пределы человеческого слухового диапазона: утверждают, что трубы этого гиганта могут воспроизводить инфразвуки и приближаться к ультразвукам.

…Но мы вернёмся пока что в Европу.

Да, пифагорова ОКТАВА стала проще. В ней сохранились только главные консонансы – прима, октава, квинта и её перевёртыш кварта. Они зафиксировались ступенями: I, VIII(I), V, IV. Круженье микрозвуков (микроинтервалов) будто распрямилось в линейку полутонов, похожих на фиксированные точки/звуки.

Но зато ОКТАВУ-модуль можно было переносить вправо-влево, по высоте звуков – вверх-вниз. От «точки отсчёта» – первой октавы.

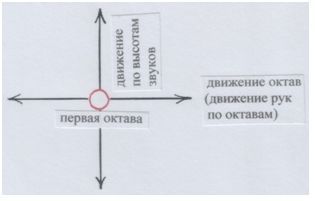
Рис. и пометки автора.

А «точкой отсчёта» является октава, которая соответствует среднему человеческому голосу (петь в первой октаве умеют все!). И, кроме того, она всегда располагается прямо напротив нас: МЫ – ОКТАВА, зеркально.

А дальше можно двигаться хоть в бесконечность!

Мы уже пробовали представить себе бесконечную клавиатуру для бесконечных волн звука и его модуляций (звук-ультразвук-инфразвук-радиоволны-элктромагнитные колебания…).

Но даже бесконечность наших мыслей, их волны-ленты мы упаковываем в буквы-точки и печатные строки. Мануалы оргáна похожи на строки в книгах, на раскрывающиеся книжные страницы…

Для того чтобы все модули-октавы сцепливались друг с другом, «склеивались», в с е звуки «через октаву» должны были звучать согласованно, точно, без колебаний вроде коммы – как в окружности совпадают начало и конец (а комма, если помнишь, свидетельствует о спирали,– в которой начало и конец не совпадают).

Нужно было найти какой-то максимально ТОЧНЫЙ, фиксированный очень ОПРЕДЕЛЁННО, коэффициент отношений между в с е м и звуками.

Вот и начались м а т е м а т и ч е с к и е эксперименты и теории.

Математики становились теоретиками музыки, музыканты-композиторы – тоже теоретиками и математиками.

Математиков (а все они в какой-то мере – наследники Пифагора по духу) будоражила мысль о «живом» Числе – т.е. о Числе, которое моделирует саму Жизнь через пропорции, отношения; это пифагорово волшебство превращения бесплотного неощутимого Числа в реальный ощутимый звук, в волны, из которых творится дыхание жизни.

Музыкантам-композиторам нужны были неограниченные возможности инструментов и новых средств для выражения этого дыхания, для переполнявших их души чувств и мыслей.

Что их так волновало?

– Захватывающая идея и захватывающий процесс под названием ТЕМПЕРАЦИЯ!

Энциклопедия:

Темперация – от лат. temperatio – правильное соотношение.

(Не могу удержаться от комментария посреди энциклопедической статьи. В этом слове – «темперация» – сошлись два смысла: temp (время, или пространство-время) и ratio (разум, рассудок). Разумное упорядочивание пространства-времени звука: ведь сама природа звука связана с природой земного времени.)

В музыке темперация – это выравнивание интервальных

соотношений между ступенями.

Темперацией занимался и Пифагор, создавая свой строй. Выравнивать интервальные соотношения помогало изменение натяжения струны и особое устроение кифары, позволявшее корректировать звуки прямо в процессе исполнения. Но в записи эта темперация предстаёт неравномерной.

Попытки перенести пифагорову струнную темперацию на флейты только подчеркнули неравномерность изначальных расчётов строя Пифагором, без этой струнной коррекции.

«Система 12 люй» приближала к решению проблемы – через полутоновые соотношения. Но проблему коммы эта система не решала.

(Интересно, что китайцы, рассчитывая свой строй, с флейтами поступали аналогично тому, как Пифагор со струной на монохорде, – когда определял основные консонансы.

Они, грубо говоря, брали трубу и нарезáли её на отрезки разной длины, которые становились флейтами. Высота звука зависела от длины отрезка трубы.

Взяли кусок – он стал изначальным тоном (примой). Отрéзали от него 1/3. Получили 2/3. Он зазвучал как квинта.

А дальше к октаве они стали подбираться через квинты (квинтовые шаги, или квинтовые ходы).

Отрезок с первой полученной квинтой они опять брали за основу и уже от него отрезáли 1/3. И так поступали до тех пор, пока не добирались до октавного звука. А это получалось через 12 шагов (операций отрезáния). Длина флейты уменьшáлась – звук становился выше.

Если длину трубы брали на 1/3 больше изначальной, звук становился ниже и звучал как кварта – ¾. Из кварт можно было получать звуки с понижением.

И всё было бы замечательно, если бы получаемый в конце концов октавный звук в точности согласовывался с примой. Но этого не получалось, – как и у Пифагора при изначальном делении струны.

(Ой-ой-ой, прости, пожалуйста, ещё на мгновение отвлечёмся. Вот тебя прямо сейчас не озарила одна изумительная мысль в связи с китайскими флейтами? – Ведь сам принцип фрактальной геометрии – он же

ф л е й т о в ы й !!! Берёшь отрезок, вычитаешь 1/3; из каждого полученного отрезка опять вычитаешь 1/3, и опять повторяешь эту же операцию, и опять… – Это же квинтовые шаги! Все фрактальные фигуры образуются квинтовыми шагами. Эту операцию с отрезками проделывали и Кох, и Серпинский, и Мандельброт… Фракталы = музыка?! Фрактальная геометрия – родом из музыки, а значит, и из астрономии?.. Ну и сюрпризы способен преподносить нам мир и модуляции Мысли!..)