Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

Для новых возможностей. Для перекрёстов правого и левого, верхних и нижних звуков – на добавочных линиях. Для связи.

В геометрии – для подобий.

Подобное размыкание мы видели и в Сфере Александера, и в пентаграммах, и в Снежинке Коха…

Принцип Фракталов: Целое делится на 3 части, вычитается 1/3 (остаются 2/3); эта 1/3 становится новым Целым, новое Целое делится на 3 части, вычитается 1/3 (остаются 2/3); эта вновь полученная 1/3 становится следующим новым Целым, делится на 3… И всё повторяется подобно. И бесконечно.

Эта же операция использована и в Принципе Флейт – для получения

т е м п е р и р о в а н н о г о с т р о я.

Логика (logos) этого строя отПЕЧАТался и в нотной записи – как в записи

з н а н и я о «фундаменте» мира, его о с н о в е.

А мы?

ОтПЕЧАТываемся мы сами в музыкальном строе и его отПЕЧАТке?

И в самом деле, наши руки – квинты влево, квинты вправо, а между, в «размыкании» рук, – узел, связь: перекрёсты мозговых полушарий, перекрёсты сосудов в сердце; наша жизнь – биологическая и душевная, её пульсация и волны дыхания, её импульсы… Вертикаль нашего тела и нашего духа, аккорд.

Мы – напротив первой октавы, соответствующей нашему умеренно-спокойному голосу. Она для нас – «диапазон отсчёта». Точка отсчёта в нашей системе координат – ДО (нота). От неё – горизонталь клавиатуры влево и вправо и вертикаль звуков вверх и вниз.

Итак, мы выбрали систему координат в мире звуков, которая соответствует нашему голосу – среднему такому человеческому голосу. А в этой системе координат выбрали нулевую точку отсчёта – ДО (нота, звук и его ключ/клавиша на клавиатуре).

От этой нулевой точки отсчёта мы можем двигаться по клавиатуре вправо, и её ключи-клавиши будут открывать ход звукам вверх (высокие звуки).

От этой же нулевой точки мы можем двигаться по клавиатуре влево, и её ключи-клавиши будут открывать ход звукам вниз (низкие звуки).

Все ключи-клавиши и звуки, которым они открывают ход, будут подчиняться двум главным ключам. Один из них – ключ «ВЕРХ» (точнее – «ВЕРХ-ПРАВО»), другой – ключ «НИЗ» («НИЗ-ЛЕВО»).

Ключ «ВЕРХ» получил собственное имя – ключ «СОЛЬ» (шаг на квинту вверх от нулевой точки ДО). «Скрипичным» этот ключ, очевидно, стали называть по трём главным причинам:

Скрипка звучит высоко. Гулкие басы – не для неё.

Скрипка – инструмент струнный. А ведь именно струны когда-то продемонстрировали нам особенности поведения звуковой волны: любая звуковая волна модулирует (изменяется) только в сторону более высоких тонов (обертонов). Попросту говоря, любая звуковая волна может изменяться только «вверх». И это было показано Пифагором на струнах.

Скрипка подражает непрерывности звуковой волны. Она подражает непрерывности голоса – переливающимся друг в друга последовательным звукам. Скрипка – сама м е л о д и я. Скрипичный ключ – ключ к связности, непрерывности, мелодии. Вот где пространство его власти.

Ключ «НИЗ» получил собственное имя – ключ «ФА» (шаг на квинту вниз от нулевой точки ДО). Шаги вниз ведут к басам (до инфразвуков). Мы знаем, что ключ «ФА» – «Басовый». В басах – мощь. И эта мощь подчёркивается звуковой массой – аккордами. Аккорды по преимуществу там, где власть басового ключа.

Как всё это умозрение о главных ключах отразилось-отпечаталось в их изображениях?

Ключ «СОЛЬ»

В его имени-названии звучат как минимум два смысла: соло и Солнце.

Соло – от лат. solus – «один».

Солнце для нас – тоже одно. Одна такая особенная звезда, хотя и подобная многим звёздам, но в то же время н е п о в т о р и м а я. Неповторимая хотя бы потому, что именно близ неё возникла Жизнь – та, какую мы знаем и какую не можем обнаружить больше нигде во Вселенной.

Так и мы, люди, подобны друг другу как вид Человек, но каждый из нас – соло: неповторим; со своим неповторимым голосом и неповторимой мелодией.

И в то же время, всё разнообразие музыки (как и неповторимых «музык» наших человечьих жизней) держится и связывается Законом квинт – квинт, движущихся вслед за Солнцем (вместе с нашей планетой Землёй) ввысь, «по Солнцу», «по свету».

Вот как смыслы ключа «СОЛЬ» могут отпечатываться в геометрии его знака:

Рис. автора.

Здесь мы увидим и вертикаль восхождения; и волну, и спираль, – которые «перетекают» друг в друга, преобразуются друг в друга и, в конце концов, утверждают квинту СОЛЬ в системе координат от нулевой точки ДО.

Здесь, на пересечениях прямых линий, а также прямых с линиями круженья, мы обнаружим и проявление равенства, и проявление неравенства – как при построении Золотого сечения. И принцип Фрактала можно обнаружить здесь.

В общем, геометрия ключа «СОЛЬ» связана с геометрией, которая выражает явление связности, непрерывности.

Мы любопытны?

Ещё как!

Мы любим тайны?

А кто же их не любит!..

У нас есть ключ. Должны быть и тайны! Ключ – к тайнам.

Тайна 1.

Входи и смотри (зрением ума, разумеется).

Рис. автора.

Вертикаль ключа, поднимаясь снизу вверх (по правилу обертонов, в соответствии с природой звука), охватывает и гептатонику ( она же – и диатоника, и гамма), и охватывает октаву (расстояние-интервал от примы – тоники – до её повторения вверху, то есть до октавного звука).

Это показывает нам система звуковых координат из линеек.

Сама вертикаль поднимается от нашей «нулевой точки отсчёта» – ДО, которую мы называем «первой» (примой), дорастает до октавного повторения примы (по количеству линеек!) и делает возвратную петлю в виде волны и спирали, которая завершается точкой, обозначающей звук (звук!) квинты.

Нижняя граница спирали намекает на то, что квинта может быть заполнена ещё одним звуком – третьим, т е р ц и е й.

И тогда образуется т р е звучие – аккорд.

Т о н и ч е с к о е т р е з в у ч и е – от начального т о н а (звука).

Любопытно, что высота столбика (или колонны?) трезвучия геометрически равна ширине спирали ключа.

А сами ноты – словно маленькие подобия этой спирали. И они – не шарики, а эллипсоиды – как наша планета Земля.

Тонкий расчёт – в основе геометрии нотного стана!

А ты помнишь то трезвучие, что явилось нам в Сфере Александера?

Вот чудо обнаружилось:

Если квинту «ДО – СОЛЬ» просчитать хроматическими звуками, то по количеству звуков она окажется о к т а в о й (до-до#-ре-ре#-ми-фа-фа#-соль – 8 звуков), а терция «ДО – МИ» окажется по количеству хроматических звуков к в и н т о й (до-до#-ре-ре#-ми – 5 звуков). Что за чудесные превращения!

Тайна 2.

Сущая головоломка!

Но – захватывающая. И уж точно – геометрическая.

Давай сделаем (умозрительно) печать звука – печать-ноту, эллипсоид: его вертикальная ось – размером от линейки стана до линейки, горизонтальная ось – чуть больше.

Пропечатаем подряд все звуки в диапазоне, который охватывает ключ «СОЛЬ» на нотном стане:

Рис. автора.

Что мы увидим?

Мы увидим, что ноты образовали восходящую линию.

Если мы измерим длину этой линии, то окажется, что эта самая длина является длиной окружности, диаметром которой является высота скрипичного ключа! Проверь сам.

(На моём настоящем рисунке высота ключа – 3,5см; длина линии нот ≈ 11см.

3,5 х 3,14 = 10,99. Ты же помнишь, что длина окружности вычисляется по формуле L=πD.)

Вот ещё как может маскироваться круженье.

Мы видим, что ноты образовали диагональ.

Ключ указывает на вертикаль, а линии нотного стана – горизонталь.

Сам собою напрашивается треугольник. Даже два треугольника.

Но мы пока поиграем-поэкспериментируем с одним.

Рис. автора.

Давай вырежем его из бумаги и накрутим на вертикаль ключа (подойдёт соломинка для коктейля диаметром с ноту на нашем рисунке).

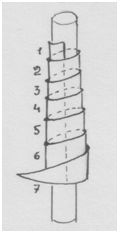
Рис. автора.

Мы увидим спираль!

Если соломинка оказалась действительно диаметром с ноту, мы увидим семь витков спирали – как семь нот гаммы (диатоники).

А ведь мы, можно сказать, закручивали диапазон октавы (от линейки до линейки, как показывает вертикаль ключа). Просто волшебство какое-то.

Есть ещё более изумительное волшебство в нашем рисунке с ключом и нотами.

Вертикаль ключа показывает нам октаву, а диагональ звуков – две октавы, укладывающиеся в октаву ключа.

Когда учёные, занимающиеся квантовой физикой (наисовременнийший раздел физики), пришли в результате своих исследований к модели пространства, они обнаружили, что само пространство обладает особой

в р а щ а т е л ь н о й с и м м е т р и е й. В этом пространстве сфера совершает полный поворот не в 360˚, а в 720˚ – то есть, поворот вдвое больший на самом деле.

Получается, что ноты демонстрируют нам аналогичное явление.

Как это явление объясняют сами физики, ты сможешь прочитать в небольшой, но очень доступной для понимания и увлекающей своей живостью статье-эксперименте Сета Ллойда, профессора квантовомеханической инженерии (из книги Джона Брокмана «Теории всего на свете»). Статья «Истинная симметрия пространства» – на страничках ниже. А вот – цитата из статьи, об итоге эксперимента:

«…вы обнаружите, что траектория мяча походит на изображённую в пространстве восьмёрку или знак бесконечности (∞) и что траектория эта совершила не один полный поворот, а два. Таким образом, истинная симметрия пространства соответствует повороту не на 360˚, а на 720˚.»

Так выглядит начало статьи об истинной вращательной симметрии пространства. Статью полностью можно прочитать в книге.

Подобное явление можно обнаружить и в эксперименте на плоскости, с кругами: когда один круг совершает поворот вокруг своей копии (как самого себя же).

Посмотри и поэкспериментируй.

Мы экспериментируем на плоскости, которая служит нам сейчас в качестве проекции пространства (как плоские тени от объёмных предметов).

Синяя точка на рисунке отмечает начальное положение.

Когда круг А сам по себе в результате своего движения будет выглядеть так же, как он выглядит сам по себе на первом рисунке (с той же синей точкой справа), это будет означать, что он совершил поворот на 360˚ вокруг своего центра.

Начальное положение круга А:

Рис. автора.

Начинаем катить круг А по линии окружности другого круга:

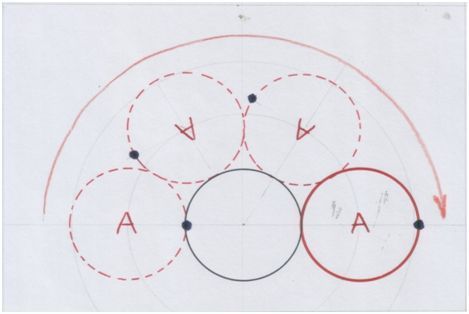
Рис. автора.

Круг А выглядит так же, как в начале своего пути. Он совершил поворот на 360˚, но в начальное положение не вернулся. Ты можешь проверить это практически, вырезав круги из картона. Ты можешь о с я з а т ь этот геометрический процесс.

Катим круг А дальше:

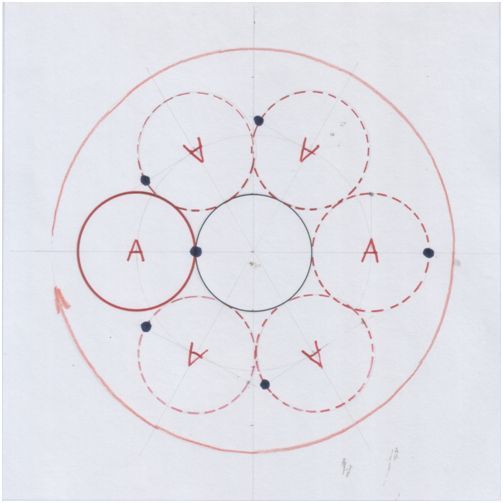
Рис. автора.

Круг А повернулся ещё на 360˚ и вернулся в начальное положение.

Итого он совершил поворот на 720˚.В этом явлении удивительно вот что:

Обе начальные окружности (чёрная и круга А) совершенно одинаковы, с одинаковым количеством точек, из которых состоят. При движении круга А все точки его окружности должны были совпасть с точками чёрной окружности «точка в точку», – допустим, на каждый градус поворота – по точке. Но градусов поворота оказалось в два раза больше, – как будто у окружности круга А и точек в два раза больше.

Подобному явлению удивлялся и немецкий математик Георг Кантор, только по поводу графиков функции. Он удивлялся тому, что количество точек отрезка равно количеству точек квадрата. Только в случае с функцией две точки координат сливаются в одну точку функции. Этот пример – из книги В.Босса «Интуиция и математика». Кантор говорил, что его рассудок отказывается это принимать, но очевидность – убедительна.

Вообще, вся эта геометрическая картинка заставила вспомнить знаменитые эпициклы Птолемея. В его космической системе планеты двигались подобным образом. Знал ли Птолемей об истинной вращательной симметрии пространства? Тогда квантовой механики ещё не было… Система Птолемея, в конце концов, была отвергнута последующими поколениями астрономов, но до сих пор даже современных учёных удивляет точность, с которой эта система предсказывала явление планет, их движение на земном небосклоне.

А теперь просто посмотри на продолжение этой геометрической игры:

Если соединить точки вращения круга А…

Рис. и пометки автора.

Лист? Сердце?

А если почаще наносить точки вращения… (Ты можешь проэкспериментировать сам, с помощью кругов.)

Рис. автора.

Сердце? Яблоко?

Согласись, что музыкальная геометрия – геометрия нотного стана – выглядит намного компактнее. И весьма лаконично она даёт нам знать («нота» – «знать») об истинной вращательной симметрии пространства. К тому же – эта геометрия звучит!

Тайна 3.

На самом деле в этой тайне для нас нет ничего тайного. Нужно только суметь

у в и д е т ь некоторые отношения, пропорции в геометрии ключа – и всё!

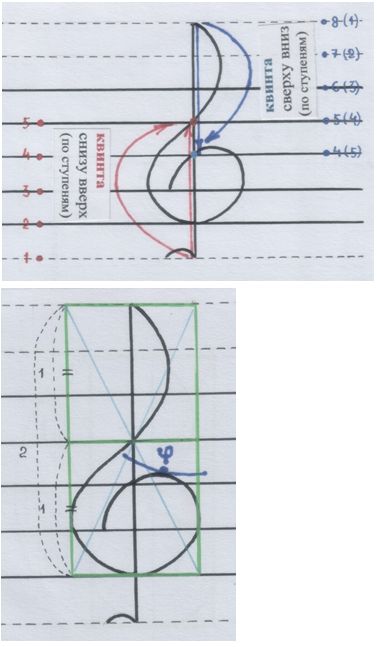
Рисунки автора.

Дальше – чуть поинтереснее. Присмотрись.

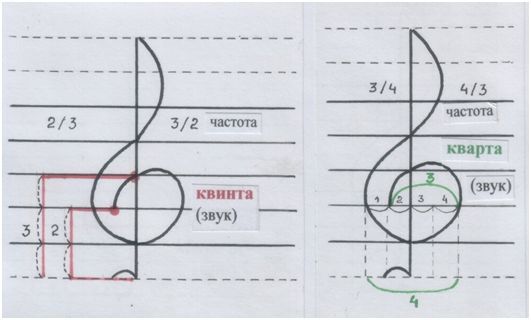
Рис. автора.

Конечная точка большого завитка может указывать и на квинту, и на кварту.

А никакого страшного противоречия нет. Мы-то хорошо знаем, что кварта – это всего лишь перевёртыш квинты: как будто её отражение в зеркале, где правое и левое меняются местами.

В конце концов, нота СОЛЬ может быть не только квинтой До-мажора, но и до-минора; может быть квартой Ре-мажора и ре-минора.

Это всего лишь говорит о великих потенциальных возможностях ключа. По опыту ты знаешь, что в с е тональности пользуются его услугами!

Так что… как посмотреть. А «как посмотреть» – это значит выбрать систему отсчёта и как и что в ней соотносить. И это – принцип относительности.

Вот! В музыке тоже действует принцип относительности.

Тайна 4.

Геометрия в пространстве.

Возьмём Геометрию за ручку и выведем прогуляться в пространство.

Мы будем с нею играть. А как же!

Пусть линия станет полоской бумаги ≈ 5мм шириной и 300мм длиной.

Раз-два-три – начало игры! Смотри и повторяй:

Рис. автора.

Совет: начинай снизу вверх, по логике звука и нотного стана. В любой игре обязательно есть логика.

Получилось?

…Результаты экспериментов принято изучать, анализировать.

И мы попробуем.

Первая петля:

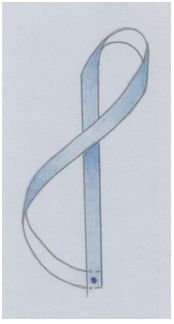
Рис. автора.

Если мы её склеим в обозначенной точке, у нас получится Петля Мёбиуса ( она же – Лента Мёбиуса). Она будет обладать свойствами Ленты Мёбиуса, даже если мы склеим концы нашей ленты под прямым углом.

Напомню свойства этой Ленты:

Непрерывность.

Парадокс: две поверхности ленты на самом деле являются одной поверхностью для скользящего по ленте пальца. Наш палец скользит всё время в одном направлении непрерывно, не перескакивая с одной поверхности на другую, но при этом бывает на обеих поверхностях.

Два – в одном, одно – из двух. Два – как одно.

Этот парадокс удивлял и Георга Кантора в связи с графиком функции (кол-во точек квадрата из координат (а их две) то же, что и в получаемом отрезке из одиночных точек. Этот же парадокс и во вращательной симметрии пространства, и… в геометрии нотного стана.

И вот ещё сам ключ намекает на это же своей петлёй.

Тут надо приплюсовать и третье свойство Ленты (Петли) – бесконечность.

Продолжим?

Рис. автора.

Сделай так и затяни аккуратно концы ленты.

…Моя лента совершила вращательное движение в пространстве и успокоилась на такой знакомой фигуре! Вот на этой:

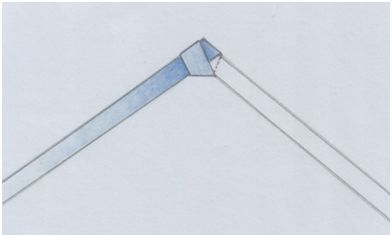
Рис. автора.

Как тебе такое?

Скрипичный ключ – зашифрованный узел?!

Выходит, что так. К тому же, узел – мы знаем – обладает свойствами Ленты Мёбиуса, когда замкнут.

Сам узел может выполнять функцию склейки в Ленте Мёбиуса. Он ведь переворачивает, меняет местами противоположности: верх-низ, лево-право.

Давай сравним ключ и свободный замкнутый узел:

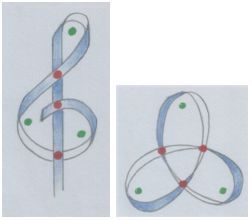
Рис. автора.

Три петли (зелёные точки). Три пересечения (красные точки).

Трезвучие.

Со второй фигурой можно играть в обращения трезвучий, если катить её, словно колесо:

Рис. автора.

Начинаем снизу и кружимся вверх – по правилу поведения звука (обертонов); слева направо – по правилу устроения клавиатуры.

Ох, что-то это напоминает…

Движение планет и самой солнечной системы тебе это не напоминает?

А давай покатаем колесо (круг то есть). Играть так играть!

Мы это делали, когда вникали в истинную вращательную симметрию пространства. Только у нас теперь будет круг с тремя точками-нотами: ДО-МИ-СОЛЬ, трезвучие.

Рис. автора.

…У меня вот что получилось:

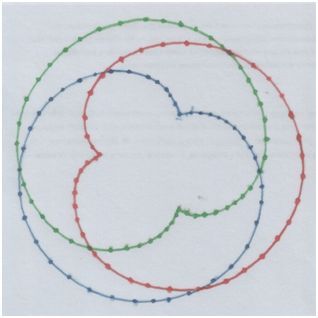
Рис. и пометки автора.

Три «кардиоиды»!

А ты можешь проверить всё сам, экспериментально. Круги в кармашке слева.

Отметь все три точки в начальном положении и продолжай отмечать, когда начнёшь катить, то есть вращать, «трезвучие». И так – пока наше трезвучие не вернётся в начальное положение.

Круговое вращение вернуло нас к петлям!

Давай поисследуем: что мы здесь интересненького разглядим?

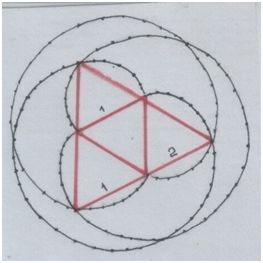
Рис. автора.

Геометрическая прогрессия (k=2, или ½).

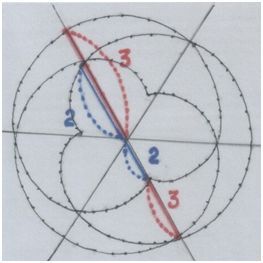
Рис. автора.

Квинтовые отношения.

Рис. и пометки автора.

Подобия с намёком на чередование.

Подобное чередование мы видели в проволочном «еже», выращенном из проволок, размеченных в соответствии с числами Фибоначчи.

Напомню:

Модель автора.

Внутри – красный додекаэдр, он вырастает в белый икосаэдр, а тот опять вырастает в додекаэдр, показанный синим цветом.

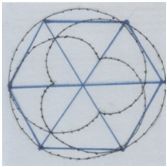
Рис. автора.

Фигура, которая образуется, когда завязываешь узел.

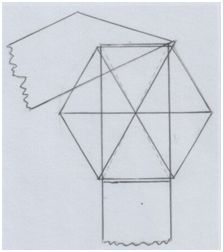
Рис. автора.

Прозрачный узел в процессе завязывания.

На первый взгляд даже трудно вообразить, что это всё – в скрипичном ключе!..

Но выходит, что в очень разных и непохожих внешне формах и явлениях можно обнаружить общую связь.

Мы всего лишь меняли точки зрения – «системы отсчёта».

Вот ещё одна точка зрения.

Что если бы мы завязали наш скрипичный ключ-узел не из плоской ленты, а из круглой верёвочки?

Чтобы завязать плоский узел, нам хватило бы шести квадратов на ленте.

Это чертёж узла.

Чтобы завязать узел из круглой верёвочки, нам хватит её длины, равной шести цилиндрическим кусочкам; при этом высота и диаметр каждого цилиндрика равны (тот же квадрат). Можешь проверить практически.

А ещё в объём этого отрезка верёвочки помещается объём девяти сфер (по закону Архимеда объём сферы, вписанной в цилиндр, равен 2/3 объёма цилиндра). 9/6 = 3/2. Квинта! Верёвочный узел тоже покажет квинту.

Но мы вернёмся к плоскости, скрипичному ключу и вращению трезвучия.

Ключ = узел.

Ключ указывает на трезвучие.

Трезвучие вращается-обращается:

1-е обращение – секстаккорд ( «секст» – «шесть», «секста» – «шестая»).

2-е обращение – квартсекстаккорд ( «кварт» – «четыре», «кварта» – «четвёртая»).

Когда мы завязываем узел, вращая ленту, первый поворот нарисует 6 в виде шестиугольника.

После следующего поворота мы продеваем ленту в петлю, и она рисует нам квадраты-кварты.

Рис. автора.

Затянутая петля превращается в пятиугольник-квинту. А в квинту заключено и трезвучие в своём начальном виде – из двух терций.

Выходит, геометрия скрипичного ключа содержит в себе намёк и на обращения трезвучия: секстаккорд и квартсекстаккорд. Удивительны свойства этого ключа!

А для чего вообще трезвучиям нужно вращаться?

А для того же, для чего вращаются электроны в атомах и все космические тела – для связи, для преобразований; для того, чтобы атомы с помощью электронов соединялись друг с другом; чтобы космические пылинки образовывали звёзды и планеты, а из них – галактики… Переменами и связью держится жизнь.

Тонические трезвучия тональностей на самом деле не прыгают по квинтам, когда ТОНАЛЬНОСТИ-актрисе захочется смодулировать – измениться. Они «подкатываются» к доминанте-квинте, чтобы утвердить на ней новую тонику.

Как это может происходить?

Если бы мы захотели запечатлеть этот процесс модуляций с помощью ключей-клавиш клавиатуры…

Впрочем, посмотри на страничках ниже. Вот что у нас получилось бы. Башня! В целых две страницы. Довольно громоздкая геометрия.

Геометрия нотной записи, конечно же, выглядит компактнее.

Рис. и пометки автора.

Две страницы (которые ниже) упаковались, сжались в две строки.

Рис. автора.

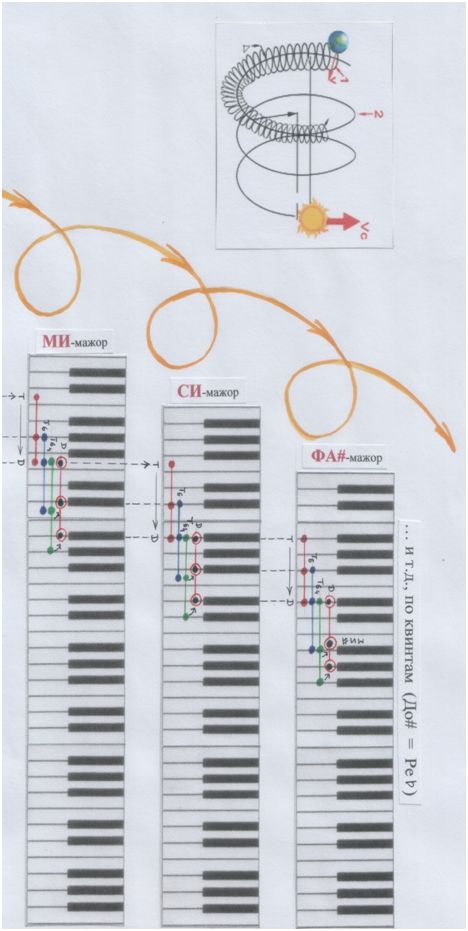
Рис. автора.

Как в данном случае происходит модуляция по квинтам?

Тоническое трезвучие, обернувшись квартсекстаккордом, оказывается на доминантном звуке (на квинте). И тут срабатывает гравитация, притяжение, «магнитное поле» доминанты. И эта доминанта перетягивает верхнюю терцию тонического квартсекстаккорда к себе поближе и превращается в новое трезвучие, с новой тоникой.

Рис. автора.

Сила притяжения звуков! Эта сила и связывает, и влечёт к переменам.