Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

Попробуем проследить именно п о с л е д о в а т е л ь н у ю связь между всеми звуками. Сомневаюсь теперь, что она будет прямолинейной. Увидим.

Я буду прослеживать карандашом. А ты сможешь повторить путь карандаша пальцем.

Это уже на следующей странице.

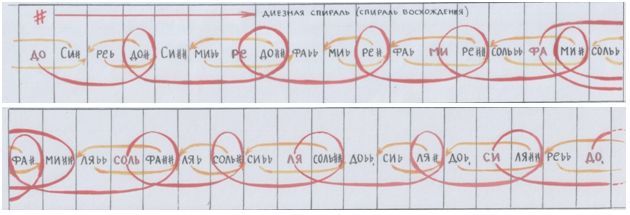
Рис. автора.

…Кажется, вот теперь вырисовывается действительно п о с л е д о в а т е л ь н о с т ь. И она – не прямолинейна. Пружина! Спираль. Пока что – спираль восхождения. На этот взлёт-восхождение намекают диезы.

…Полетим сверху вниз – от верхнего ДО к нижнему. Путь укажут бемоли.

Рисунки автора.

И снова – пружина-спираль.

Совместим эти противодвижения звуковых потоков:

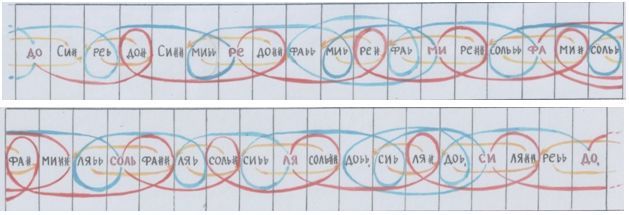
Рисунки автора.

Вот эти противодвижения и побуждают звуки к колебанию ( на ленте – это показано «вращающимися» звуками). Когда-нибудь мы непременно услышим, как каждый звук «растекается», словно круги на воде, волнами. И это показывают микроинтервалы – те самые к о м м ы, в окружении которых каждый основной звук и оказывается.

Если тебе интересно, Солнце в нашей галактике тоже движется не прямолинейно, а по спирали – закручивающейся в противоположную земной спирали сторону: Земля, допустим, вращается слева направо, а Солнце – справа налево. Противодвижение.

По ступеням музыкальной лестницы тоже можно кружить: поднимаясь на квинту – спускаясь на кварту; снова – вверх на квинту, вниз – на кварту; квинта-кварта, квинта-кварта… Подобие октавы внутри самой октавы.

Древние греки знали толк в подобиях.

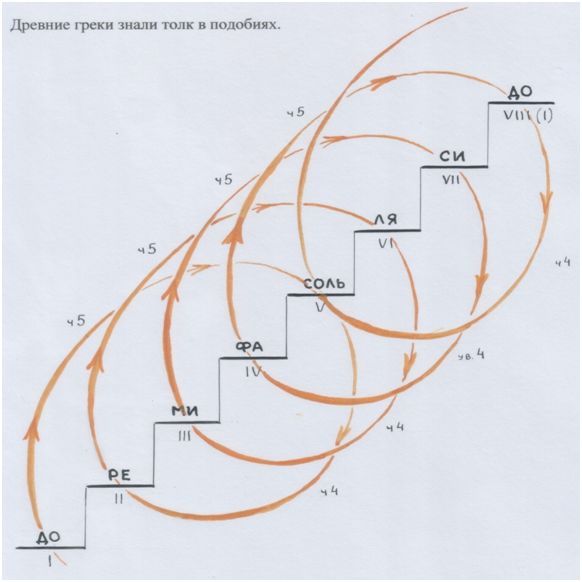
Рис. автора

Рис. автора

Восемь витков октавной спирали. На каждую ступень – по витку.

А «веретено» – из квинт-узлов, которые превратились в ступени (вспомни соответствующую модель).

Модель автора.

Знаешь, чтó поразительно? –

То, что звуковая модель космоса, сотворённая Пифагором, описывает своим устроением-строем (если его изобразить графически) геометрию пространства-времени новейших времён!

Надеюсь, к тебе когда-нибудь прилетят книги очень известных, уважаемых в научном мире и популярных американских физиков-теоретиков Лизы Рэндалл и Брайана Грина. Они – о знаменитой Теории струн, которая описывает современный взгляд на устройство Вселенной. Книга Лизы Рэндалл так и называется: «Закрученные пассажи» (французское слово «пассаж» означает «проход», пробег, связь; в музыке – связанный пробег по звукам; в литературе – связанный пробегом мысли фрагмент текста).

Да сама история новой физики началась с «геометрии кружения» – геометрии Римана и Лобачевского.

Разве мог Пифагор ещё т о г д а (!) знать обо всё этом?!

Загадка…

Загадка противодвижения времён: двигаясь в Будущее, мы всё больше удивляемся Прошлому.

Может быть, и вправду у Времени два потока: один – это видимое нами пространство-время; а другой – незримое время, которое потихоньку «уменьшает» нас, делая нашу жизнь (видимую) конечной. (А невидимая – бесконечна…) Вот и Солнце, вроде бы двигаясь «вперёд», на самом деле пятится назад по созвездиям Зодиака, проходя их в обратном порядке… Уж это Пифагор знал.

Таким образом и встретились два потока в его строе.

Если ты приглядишься повнимательнее к этому строю (на лентах), особенно к концам, где ДО внизу и вверху (слева и справа), то пожалуй, сообразишь, что строй-то – бесконечный! По аналогии его можно продолжать новыми октавами и вправо, и влево… Но Пифагор остановился на одной октаве.

Ему оказалось достаточно и одной октавы, чтобы выразить весь строй космоса. Другие октавы – это п о д о б и я одной.

Да и на лиру не поместить бесконечное количество струн.

Как звучит эта головокружительная космическая геометрия?

Головокружительно!

Волшебно!

Магически.

Нужно просто услышать древнегреческую КИФАРУ.

Кифара – это мужская лира, лира богов.

Её представляет канадский музыкант, певец, писатель, журналист, актёр ( в своём роде гений!) Петер Прингл.

Звуки кифары и в самом деле могут вызвать лёгкое кружение головы.

Они похожи на покачивающиеся в душистом тумане миражи. Такой туман поднимался из расселин дельфийских гор, и в этих испарениях жрицы солнечного Аполлона – пифии – провидели, прорицали будущее, судьбы людей, богов и мира. Слушая кифару, понимаешь, почему Пифагора звали Пифа-гор: прорицающий будущее на вершине – где небо дарит земле свой поцелуй.

Внимая звукам кифары, душа превращается в волны. И в этих волнах мерцают звёзды и плывут планеты…

Если пожелаешь увидеть это наяву, найди в Википедии статью «Луна». Там есть анимация: волнующаяся Луна. Взгляни – и внутри себя ты услышишь кифару.

Ты услышишь, наконец, загадочные неуловимые к о м м ы. Они послушны только кифаре, – потому что исполнить их можно лишь на этом удивительном инструменте. Специальные рожки и диски были изобретены греческими мастерами, чтобы музыкант мог чуткими движениями рук менять мгновенно едва-едва натяжение струн прямо во время исполнения. Какого же незаурядного исполнительского мастерства требовал этот божественный инструмент!

Учти, он может опьянить без вина…

В твоём Музыкальном энциклопедическом словаре должна быть статья про кифару. И в этой статье должно сообщаться о том, что от слова «кифара» произошли названия таких инструментов, как гитара и цитра. Когда какое-то слово пускается в странствие по Реке Времени, его звуки и буквы начинают колебаться, словно пифагоровы коммы. «К» может вибрировать, превращаясь то в «Г», то в «Ц»; «Ф» превращается в «Т». Если «К» превратится в «Ц», получится «цифара» – «цифра» (цитра-цифра).Забавно? Хотя, если знать, что струны кифары в ы ч и с л е н ы Пифагором, весь её строй основан на Ч и с л е, – то нет, не забавно, всё всерьёз.

Поющая математика!

Именно п о ю щ а я. Потому что кифара, по замыслу своих создателей (богов, не иначе, – пример с Гермесом), подражает г о л о с у. Она предназначена для исполнения м е л о д и и. Аккорды на кифаре не исполняют; изредка – благозвучные интервалы. Или – арпеджио (арфеджио – от «арфа»).О секундах и септимах речи быть не может! Это – д и с с о н а н с ы. А кифара – для прославления божественной г а р м о н и и, посредством к о н с о н а н с о в.

Вот когда секунды и септимы звучат не одновременно взятыми звуками, а перетекающими один в другой последовательно, получается льющаяся мелодия. Эти интервалы необходимы для с в я з и, и в этой роли они прекрасны! И совсем не противоречат гармонии.

Кроме того, предполагается, что «пение» этого инструмента – сольное.

С о л о. Подобно СОЛнцу, которое – о д н о. Кифара – голос Аполлона, бога Солнца.

Ты обратил внимание на то, что в древнегреческих росписях кифареды (исполнители на кифаре) – это боги, герои или крылатые музы? Личности космического масштаба!

Греки изображали их в окружении в о л н.

Странные волны. Прямоугольные.

Если помнишь, эти волны называют м е а н д р а м и.

Прямоугольное круженье. (Музыкальная геометрия древних моделей мироздания. Кифара и Октавный принцип не только в музыке.)

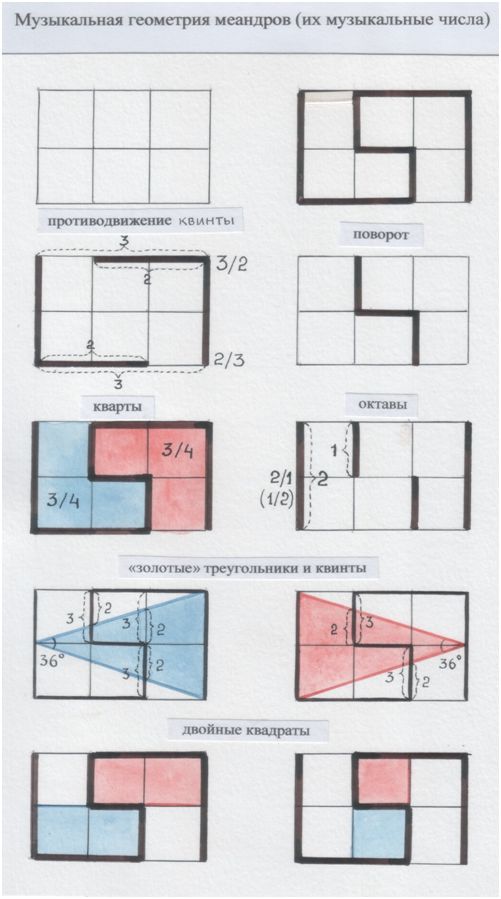
Рис. автора.

Рис. автора.

Две взаимно обратные спирали:

Рис. и модель автора

Рис. автора.

… и следы меандров в математике после античности – в картинках на следующих страницах:

Тебя уже осенили какие-нибудь догадки по поводу меандров?

?

Но почему же у греков эти меандры-волны, меандры-мелодии всё-таки

п р я м о у г о л ь н ы е?

Может быть, потому что для нас, живущих на поверхности Земли, так важен именно п е р п е н д и к у л я р. Он знаменует собою у с т о й ч и в о с т ь в этом зыбком, неостановимом, вращающемся космосе.

Но.

Ведь он запрятан – незримый! – внутрь Земли, Луны, Солнца, иных планет и звёзд, галактик, – как ось посреди экватора. Он запрятан внутрь кристаллов, растений, животных, нас самих. Он запрятан внутрь атомов, внутрь того, что само по себе незримо: внутрь электромагнитного поля. Ты, наверное, знаешь, что магнитное поле и электрическое – взаимно перпендикулярны.

Когда-то Ум человеческий сказал сам себе: возьму-ка я этот посох, чтобы дойти до самого сердца мира…

И что же стало?

Появилась линейка, появились меры, появились числа. Появились модели всего того, что познавал человек: архитектура, механизмы. Появилась механика Ньютона и система координат Декарта. Для чего? – Дабы познать само круженье в конце-то концов…

Сколько лет этому посоху познанья?

Древнегреческие меандры… В них – намёк. А от них в какую глубь и даль простирается путь?

Посмотрим?

Рис. и модель автора.

О пирамидах некоторые исследователи-египтологи пишут, что они имеют подобную наземной подземную часть. Может быть…

И если так, то это можно промоделировать знакомым тебе правильным многогранником, – одним из пяти, в которых находят золотую пропорцию.

Октаэдр! («окто» – «восемь», «эдр» – «грань»)

Это – о симметрии нашей планеты. Симметрии о к т а э д р а.

Вот куда нас завёл наш посох познания – перпендикуляр! – В самую сущность строения-строя Земли.

И Земля кружит в электромагнитном поле, где тоже действует перпендикуляр. Самый прочный на Земле кристалл – алмаз – сотворяясь глубоко в недрах земной коры, в своём строении воспроизводит действие этого поля и … повторяет симметрию Земли:

Так что меандры мы вполне можем вообразить развёрткой на плоскости нашей планеты – в геометрическом исполнении, конечно же.

Каким же образом это связано с о к т а в о й Пифагора?

Геометрически связано.

Через кварты! – «Кварта» – «четыре». Квадратное число. Квадрат.

Рис. и пометки автора.

Октава («восемь») – есть у д в о е н н а я кварта («четыре»).

Удвоение – признак г е о м е т р и ч е с к о й п р о г р е с с и и (k=2).

Кварты намекают нам на присутствие в музыкальном строе геометрической прогрессии.

Как ещё иначе проявляет себя геометрическая прогрессия в музыке?

Метрическим делением, нотными длительностями, градациями в р е м е н и звучания звуков.

ВРЕМЯ.

Вот ещё с чем связана геометрическая прогрессия в музыке.

Изображением привычных нам нот это очень просто продемонстрировать:

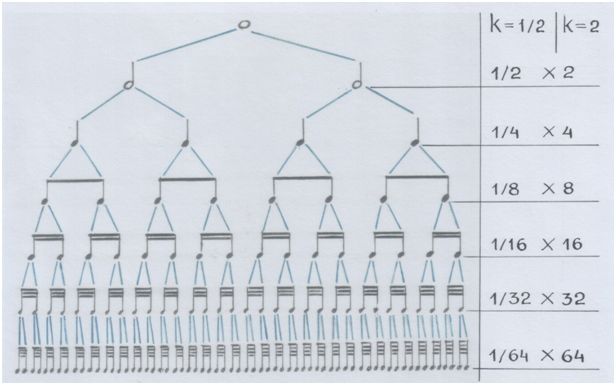
Рис. автора.

Дальше – 1/128 х 128; 1/256 х 256… до неразличимости, которая покажется сплошной полосой, похожей на шум («белый шум»?).

Если представить, что и длительности нот подражают принципу октавы, то деление звука-длительности на два будет подобно делению октавы на кварты:

Рис. автора.

Но у нас ещё есть ноты с точками…

То есть п о л т о р ы ноты: 1,5 или 3/2.

Подобие к в и н т ы.

… Что-то напоминает микро-октавы в октаве Пифагора. Так и до подобий комм комм комм… можно добраться:

Рис. автора.

Хорошо, что такое в нашей музыке не встречается. Попробуй высчитай такую длительность! – и звёзды успеют погаснуть в перерывах между звуками…

Интересно, кáк древние греки обозначали длительности?

Вот древние египтяне могли воспользоваться иероглифами своего излюбленного Уаджета.

А древние греки… Спросить бы у них…

Впрочем, у них ведь были какие-то особенные точки для обозначения отрезков текстов различной длины. И назывались они : апотома – для обозначения длинного отрезка текста; лимма – для обозначения средней длины отрезка текста в длинном отрезке; комма – для обозначения самого маленького отрезка. Д л и т е л ь н о с т и звучания речи!

А нам эти знакомцы являлись в образах музыкальных интервалов, из которых Пифагор сотворял микро-подобия октавы…

Значит, для древних греков принцип октавы действовал и в длительностях.

И речь – разве она не музыкальна?

Где только не проявлял себя принцип октавы! Его вещественными моделями служили даже произведения архитектуры!

Архитектуру называют застывшей музыкой.

Давай посмотрим ещё и на такую музыку.

Парфенон – октава.

Самый знаменитый – после египетских пирамид – памятник архитектуры.

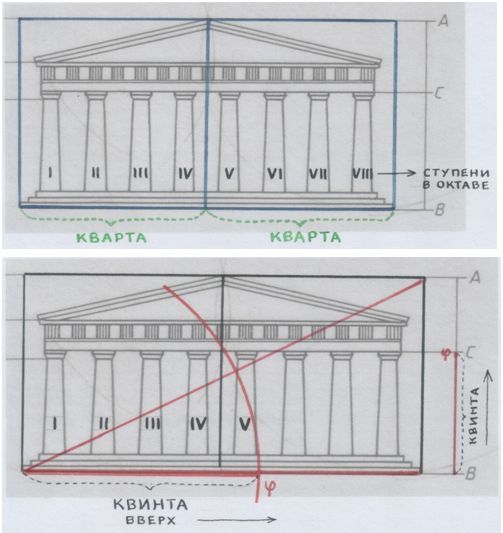
Рис. и пометки автора.

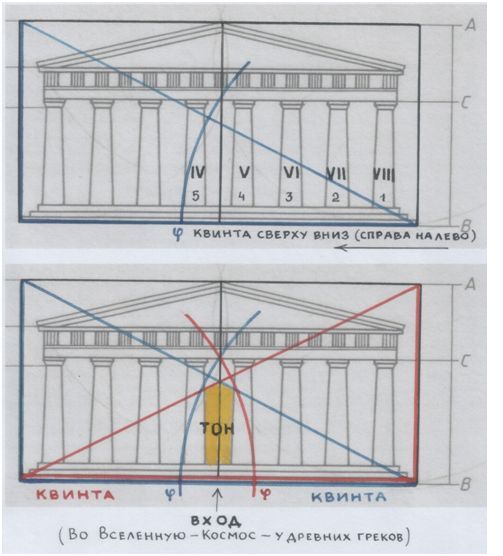
Рис. и пометки автора.

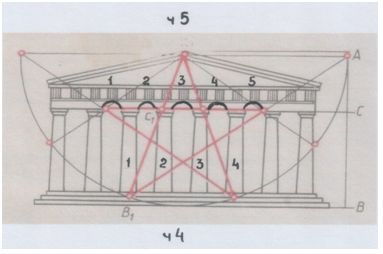
Рис. и пометки автора.

ПОДОБИЯ

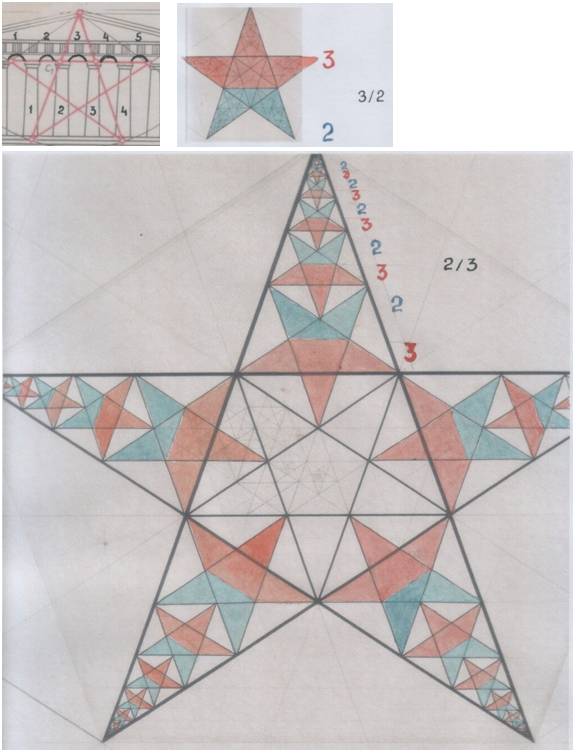
Рисунки автора.

Парфенон посвящён Афине Парфенос.

Чем же так замечательна эта богиня, что ей греки посвятили самый знаменитый храм Древней Греции?

Она рождена верховным богом Вселенной Зевсом из его г о л о в ы!

Не из периферии мозга – тела, а из самого его эпицентра (!), из начала начал жизни.

Голова Зевса, расколовшись н а д в о е (k=1/2), вытолкнула, выпустила из себя в мир ту, что назвали Мудростью. Афина – богиня мудрости.

И Афина же – богиня войны.

Как это понимать?

У Афины в данном случае есть эпитет (что-то вроде прозвища, символического имени) – Парфенос. Это греческое слово означает «дева». Афина-Дева. И в этом особом случае (Афина – производная г о л о в ы) речь идёт не о телесном признаке человеческого пола («пол» – всего лишь «половина», половина Человека вообще, мужская или женская половины), а о той Мудрости, которая может проявлять себя в любом человеке, независимо от его пола.

Афина – не «половина», а с о в е р ш е н с т в о, ц е л о с т н о с т ь, которую способен восстанавливать из отдельных элементов мира разум. «Целостность» и «мудрость» – вот из этих слов сложено слово «целомудрие», иначе – «девственность».

Афина – это мир человеческого Духа, разума, ума, интеллекта. И в мире Духа беспрестанно идёт война со слабостями, к которым склоняет тело – ленью, расслабленностью, алчностью, завистью, жаждой телесных удовольствий… и т.п. Война-борьба. Со всем тем, что ведёт к разрушению Целого, к обидам и горечам, к страданиям.

Афина опирается на щит. Она – защитница. Её война – за истину, а не агрессию и разрушение. Её копьё – вертикаль Духа, перпендикуляр. Оно не агрессивно, но всегда наготове. В её правой руке – крылатая Нике с лавровым венком славы, само вдохновение и Победа. Она же – в центре на шлеме, между смелых коней, подобных той страсти, что влечёт человека к познанию. Рога её шлема – не острия, а завитки-спирали.

Афина – война-борьба человеческого Духа в самом себе, за своё совершенство. Она – призыв к у с и л и ю над собою (помнишь? – «жизнь – это усилие во времени»…). Призыв к д о м и н а н т е.

Разве не то же – в музыке?

Когда ты перевернёшь эту страницу, то увидишь п л а н Парфенона, его внутреннюю геометрию.

В этой геометрии числа показаны точками-колоннами.

Ты найдёшь и место Афины в геометрическом космосе Парфенона.

Если присмотришься повнимательнее, то пожалуй, ты поймёшь, почему афиняне облачили свою богиню-мудрость в одежды из золота.

Вещественное может выражать НЕвещественное – то, что Платон называл и д е е й. И когда происходит так, то вещь становится с и м в о л о м (знаком) того незримого, что есть, но глазами сразу не увидеть, руками не потрогать. Постигнуть это можно только зрением ума – умозрением.

Твоё умозрение не сможет не заметить, сколь музыкален строй Парфенона!

Он весь – из консонансов. Струнная теория Пифагора – в камне.

Этот очень вещественный материал сквозь века донёс до нас очень невещественную идею такого универсального м о д у л я, который способен объединить земной и космический миры, миры веществ и существ, предметов и явлений. В этом модуле – неразлучная парочка: геометрическая прогрессия (k=2, k=1/2) и золотое сечение. И называется он ОКТАВА.

Модуль – от лат. modulus – «мера».

План Парфенона и консонансы.

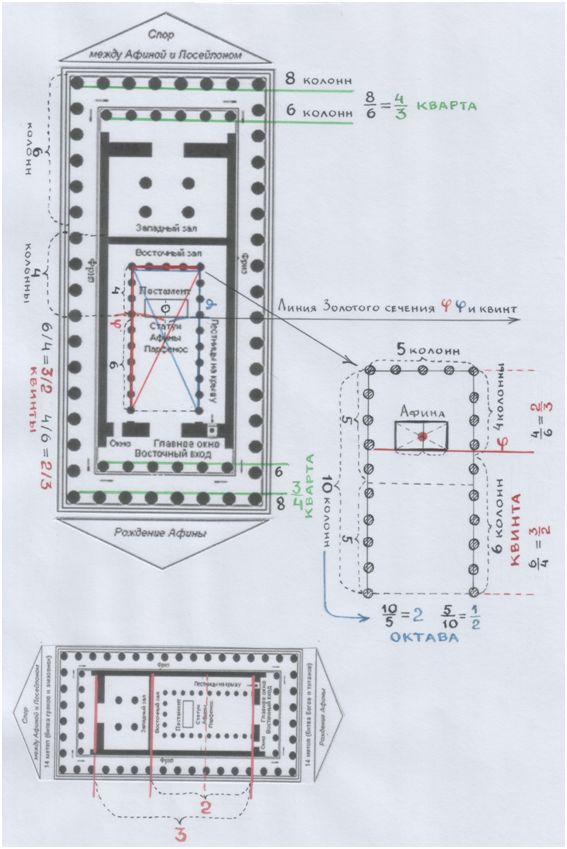
Рис. и пометки автора.

Конечно, с помощью п р я м ы х линий измерять всё проще и удобнее: линейка и шкала мер на ней.

Но вот как же исхитриться этой п р я м о л и н е й н о с т ь ю передать к р у ж е н ь е, которым исполнен мир, тем более – измерить это круженье?

Как смоделировать мир в т о ч н о с т и таким, каков он есть?

Где прямолинейность – там доступна точность в измерениях. Где криволинейность, круженье – там начинаются неточности…

Ох, эта загадка, эта проблема озадачивает, манит, тревожит великие человеческие умы не одно столетие и даже тысячелетие по сей день.

Древнеегипетские жрецы (читай: учёные), пытаясь добраться до сердца этой тайны, нашли свой способ распрямления окружности с соблюдением точных линейных мер. Оказалось, что это возможно только в одном-единственном случае. 12-мерная окружность при этом превращалась в 12-мерный

п р я м о у г о л ь н ы й треугольник с точными мерами сторон: 3,4,5. – В общем, известный тебе египетский треугольник. Он и знаменовал собою круженье Времени (пространства-времени): год из 12 месяцев.

На какую мысль натолкнул этот эксперимент?

– Прямой угол (перпендикуляр) может стать ключом к исчислению круженья.

Древнегреческая мысль подхватила эту идею.

Пифагор оформил её в свою знаменитую теорему.

Новую проблему поставила гипотенуза. Её упрямая неточность для всех «неегипетских» случаев с прямоугольным треугольником.

В гипотенузе оказался корень проблемы. Она навсегда оказалась связанной с исчислением (извлечением) корня. А корень упрямо оказался связанным опять же с неточностью…

Выходило, что корень проблемы круженья – в линейной неточности.

А что же тогда т о ч н о?

Какими мерами т о ч н о можно измерить это самое круженье?

…Шумерские жрецы (читай: учёные) в поисках точности всматривались в звёздное небо.

У г л о в ы е меры!

Итак, наиболее точные меры для исчисления круженья – у г л о в ы е: у г л ы п о в о р о т а.

Вот что ещё интересно в связи с этим:

Учёные-кристаллографы (те, кто занимаются изучением мира кристаллов) тоже наиболее точными признают именно угловые меры, когда возникает необходимость определить вид минерала. Ведь внешне минералы – неправильной формы, разных размеров. А вот их кристаллические решётки (если изучить их изнутри) всегда неукоснительно соблюдают одни и те же углы в расположении атомов, характерные для определённых минералов.

А что удивительного? Ведь их формируют магнитные поля своим круженьем…

Для греков (в отличие от шумеров) был важен именно п р я м о й угол, перпендикуляр.

Он давал возможность создавать вещественные модели космоса в земных условиях (архитектура). И вся их геометрия связана с прямым углом. Земля – космическое тело, и космос являет себя в земной жизни. И древнегреческие боги тоже ходили по земле, соединяя нашу планету и мир людей со Вселенной.

Слова «градус» древние греки ещё не употребляли. Они измеряли угловое круженье долями прямого угла!

Вот строчка из книги «Прометеева искра. Античные истоки искусства математики» А.В.Жукова :

«…углы Аристарх выражал не в градусах, а в д о л я х п р я м о г о у г л а».

(Аристарх Самосский – древнегреческий астроном, математик и философ III века до н.э., впервые предложивший гелиоцентрическую систему мира и разработавший научный метод определения расстояния до Солнца и Луны и их размеров.)

Вот! Слово «доля» – аналог, подобие «градуса»; прямой угол – подобие целого (360˚).

…А теперь так хочется быстренько пробежаться туда, в «Афинскую школу» (Рафаэля), где Боэций слушает Платона и конспектирует Пифагора, и ещё разочек заглянуть в его конспект и перечитать его новым озарённым умозрением!

Что там написано (по поводу октавы)?

… «Делить же он (Пифагор) начал следующим образом: прежде всего отнял от ц е л о г о одну д о л ю , затем вторую, вдвое большую, третью – в полтора раза больше второй и в три раза больше третьей, четвёртую – вдвое больше второй, пятую – втрое больше третьей, шестую – в восемь раз больше первой, а седьмую – больше первой в двадцать семь раз.»

Как-то уж очень похоже на то, что Пифагор пытался сопрячь, соединить звуковое круженье и угловое, чтобы у в и д е т ь (!) звуковую модель в своём умозрении.

Давай попробуем расписать этот текст как задачку.

«Доля» у нас неизвестное – икс х. Х может быть и звуковым интервалом, как прежде, и угловой мерой – если, как Пифагор, мы захотим у в и д е т ь звук как геометрию. Эти угловые меры мы можем обозначить привычными нам градусами вместо греческих «долей».

Рис. автора.

С седьмой доли начинается п о д о б и е. Подобие совокупности всех предыдущих.

В интервалах она даёт выход на лимму и подобие октавы в микроинтервалах, если помнишь.

А дальше – знакомые картинки.

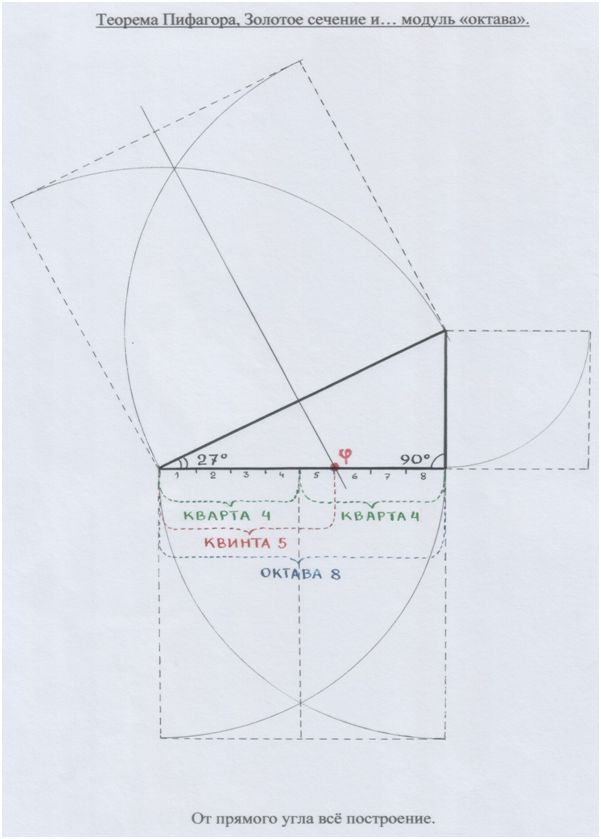
Рис. автора.

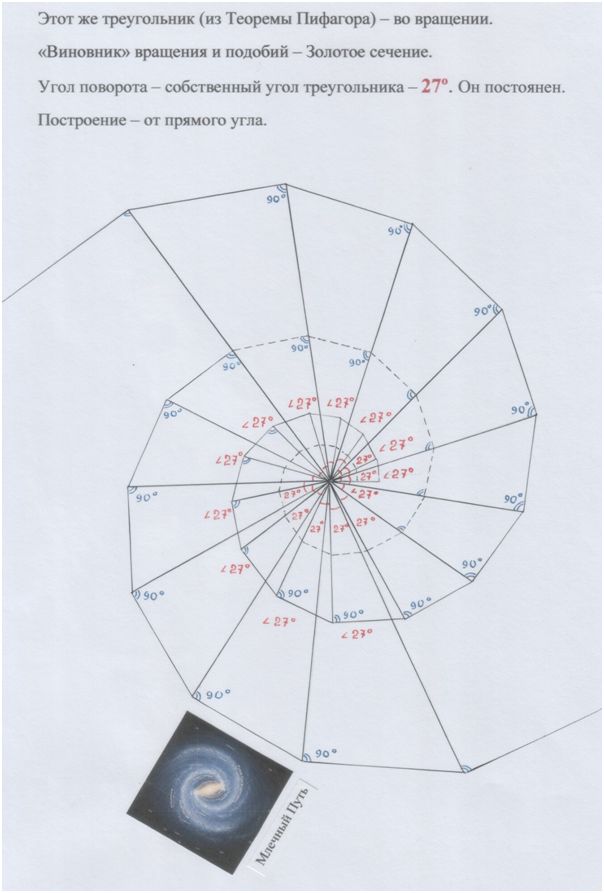
Рис. автора.

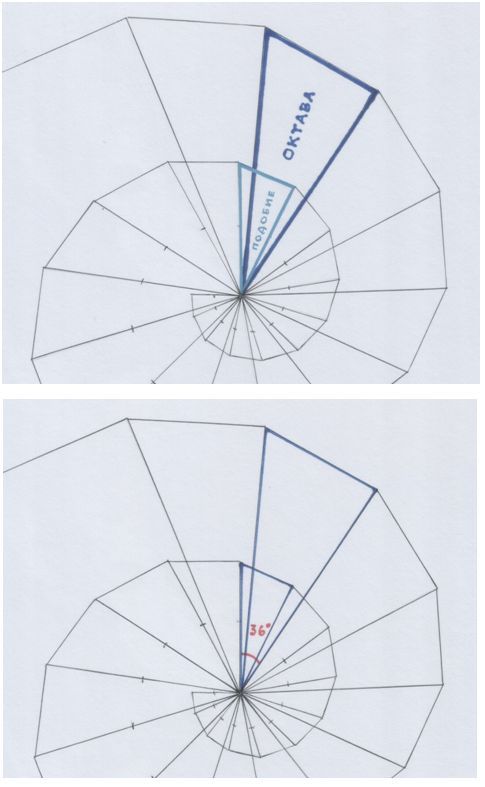
Рис. автора

Октава и её подобие, образующие «золотой» угол – 36º: как 36 звуков в пифагоровой октаве.

Постичь круженье, тем более измерить его – задачка, конечно, не из лёгких.

Перевести круг в треугольник – была замечательная идея египтян.

Сопряжение угловых поворотов и прямых линий впоследствии произвели на свет тригонометрические функции. Роль треугольника в измерении круженья оказалась неоценимой. Смысл понятия «тригонометрические функции»: «функция» – «роль», «дело»; «тригонон» (греч.) – «треугольник»; «метрео» (греч.) – «измеряю». Но нужно отметить, что с целочисленными результатами измерений здесь всегда проблема: ты знаешь, что значения синусов, косинусов, тангенсов, котангенсов – не целочисленны.

Да, всё то, что не прямолинейно, не хочет поддаваться простому, а зачастую и точному измерению. В состав формул для измерения круженья вообще входят б е с к о н е ч н ы е числа. Их называют т р а н с ц е н д е н т н ы м и: «транс» – «перенос». Эти числа переносятся через все пределы-границы, не знают конца.

Таких чисел три:

Знакомое тебе π, знакомое φ, и ещё е – число Эйлера, которое входит в состав натуральных логарифмов.