 Полная версия
Полная версияНаселение Земли как растущая иерархическая сеть
Так, например, одна половина популяции может находиться на Земле, а вторая – в другой галактике, и тем не менее закон dN/dt = αN, описывающий суммарный рост, будет по нашему определению причинным, хотя причинной связи между этими половинками не может быть в принципе.
Но если причинный закон роста будет нелинейным, например, квадратичным dN/dt = αN2, то рост любых двух частей такой популяции должен быть связан причинно, т. к. ежегодный прирост численности на единичную репродуктивную ячейку популяции dN/N = αNdt будет в таком случае зависеть от общей численности N. В этом заключается качественное отличие причинного нелинейного от причинного линейного закона роста популяции.
* * *Как линейный, так и нелинейный закон роста популяции могут и не быть причинными законами, т. е. могут описывать непричинную связь между численностью и скоростью ее роста. Пример такого закона мы рассмотрим ниже. И, наконец, может случиться так, что рост численности популяции будет, например, гиперболическим, но никакого закона, описывающего такой рост в форме автономного уравнения, т. е. уравнения, правая часть которого зависит только от N, – не существует.
Рост численности будет зависеть в этом случае не только от внутренних причин, но и от внешних условий, и в правой части уравнения, описывающего такой рост, будет присутствовать в явном виде время: dN/dt = F(N,t). Примером такого роста может служить, например, рост суммарной растительной клеточной массы в весенний период в Северном полушарии. Даже если бы этот рост оказался гиперболическим, считать, что он обусловлен положительной обратной связью второго порядка между растительной массой и скоростью ее роста, очевидно, нельзя.
Переменная-причина и переменная-следствие могут меняться местами даже при рассмотрении одного и того же функционального закона. Так, при сжатии внешней силой идеального газа в замкнутом сосуде, связь между приростом давления и уменьшением объема газа за малый промежуток времени будет причинной.
Причем прирост давления – причина, а уменьшения объема – следствие. При свободном расширении сжатого газа причинные переменные меняются местами: прирост объема за малый промежуток времени приводит к убыли давления.
В приведенных здесь примерах причинных законов с преддетерминацией, связывающих две переменные, причинная переменная может быть как дифференциальной, так и интегральной. Тогда как переменная-следствие всегда является дифференциальной. Такая асимметрия связана с тем, что событие-следствие, как это обычно принято считать, должно быть локализовано в пространстве и во времени и целиком обусловлено событием-причиной.
Это событие-следствие может быть малым приращением пути, пройденного телом, или приростом численности популяции за небольшой промежуток времени. Т. е. пройденный телом путь может быть причиной значения его скорости в данный момент времени (движение частицы в однородном силовом поле) и текущая численность популяции может быть причиной ее текущего естественного прироста, а не наоборот.
* * *Примером непричинной (не ПОС и не ООС) связи между переменной и скоростью ее роста может служить связь между средним ежедневным выпуском продукции на некотором предприятии и общим ее количеством, выпущенном с начала года.
Пусть в январе запланировано выпустить некоторое количество продукции, а за каждый последующий месяц в течение года ее выход по сравнению с предыдущим должен быть увеличен на десять процентов. При этом количество ежедневно выпускаемых товаров может быть любым, т. е. никак планом не регламентируется.
Но в конце последнего дня каждого месяца план должен быть выполнен, т. е. должно быть произведено запланированное количество продукции (не больше и не меньше). Связь между усредненным за некоторый промежуток времени ежедневным и общим количеством продукции, выпущенным с начала года, будет в этом случае функциональной, непричинной. Функциональной в том смысле, что эти средние связаны вполне определенной аналитической зависимостью, а непричинной – в том смысле, что не текущее количество выпущенных товаров причинно определяет прирост и не текущий прирост причинно задает это количество, а делает это управляющая система, реализующая закон, по которому растет как ежедневный прирост продукции (как управляемый случайный процесс), так и общий ее выпуск (как управляемый, эквифинальный, нестационарный случайный процесс), полностью определяемый его суммарной величиной.
Т. е. вероятностный закон, связывающий мгновенное общее количество выпущенной с начала года продукции со скоростью ее производства в каждый момент времени, описывает непричинную, функциональную, а не причинно-следственную связь. Нестационарный управляемый случайный процесс N(t) (количество товаров, выпущенных к моменту времени t) может считаться эквифинальным в том смысле, что в конце каждого месяца N(t) будет отличаться от планового значения на некоторую относительно небольшую предзаданную величину.
Т. к. количество выпущенных товаров возрастает ежемесячно в одно и то же число раз (в 1,1 раза), то вероятностная, непричинная зависимость между скоростью производства и полным количеством выпущенной с начала года продукции будет примерно линейной. А зависимость количества произведенных товаров от времени в течение года в первом приближении – экспоненциальной.
Если бы такой прирост планировался не на постоянных, а на сокращающихся по закону прогрессии к точке сингулярности отрезках времени, то рост выпущенной продукции был бы гиперболическим. Причем в простейшем случае такого роста зависимость между скоростью производства и общим выпуском товаров была бы уже не линейной, а параболической. Т. е. описывалась бы уравнением квадратичного роста dN/dt = αN2, которое не определяет в данном случае автокаталитический процесс и не является причинным законом. (По такому же закону растет и численность населения Земли. И уравнение квадратичного роста, связывающее эту численность и скорость ее роста, может и не быть причинным законом.)
Здесь мы имеем дело с причинным, вероятностным, целевым (телеологическим) законом или законом с постдетерминацией, связывающим количество выпускаемой ежедневно в течение каждого месяца продукции (случайную переменную-следствие) с плановым общим ее выходом в конце каждого такого месяца – причинной целевой переменной, значение которой предопределено в будущем.
* * *При анализе причинного закона с преддетерминацией недостаточно указать формулу, аналитическую зависимость, связывающую каузальные переменные. Необходимо еще описать КАК в пространстве и во времени рост переменной-причины приводит к росту (уменьшению) переменной-следствие.
Данное нами определение причинного закона для двух переменных сформулировано для конкретной задачи исследования законов роста численности популяций и, в частности, закона роста численности населения Земли. Мы не ставили перед собой задачи всесторонне исследовать этот сложный вопрос и давать наиболее общее определение.
* * *Дадим определение закона квадратичного роста как причинного закона роста численности популяции, рассматривая dN/dt = N2/C как уравнение в конечных разностях (1А), рис. 3.
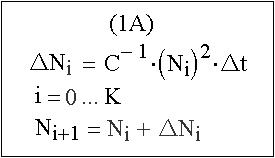
Рис. 3. Решение задачи Коши методом Эйлера.
Пусть в начальный момент времени t0 численность популяции равна N0. Разобьем промежуток t − t0 на интервалы равной длительности, причем шаг Δt можно сделать «сколь угодно» малым.
Введем сеточную функцию дискретного аргумента, вычисляемую в узлах сетки. В момент t1 = t0 + Δt найдем прирост численности ΔN0 по (1А) и определим ее новое значение N1 = N0 + ΔN0.
Продолжим итерации, опираясь на (1А) как на рекуррентное соотношение, и вычислим значение численности во всех узловых точках, решив, таким образом, простейшую задачу Коши одношаговым методом Эйлера.
Закон квадратичного роста dN/dt = N2/C можно считать причинным законом роста популяции в том, и только в том случае, если действительный рост численности этой популяции в точности соответствует этому математическому итеративному алгоритму и удовлетворяет двум следующим условиям:
1. Для описания роста численности может быть введен отрезок времени Δt, с одной стороны, достаточно малый для того, чтобы закон роста мог быть сформулирован в форме дифференциального уравнения, а, с другой стороны, достаточно большой для того, чтобы смогли заработать механизмы этого роста, которые для каждой модели свои. Для изобретательской теории Коротаева Δt – это то время, за которое изобретения «растворятся» в Мир-системе и дадут прирост ΔN. Для феноменологической теории Капицы – это время достаточно большое для того, чтобы накопленная в Ойкумене информация дала неслучайный прирост, пропорциональный квадрату числа связей.
2. Рост численности популяции на любом конечном отрезке времени может быть представлен как причинно-следственная цепь событий, в которой каждое предыдущее событие есть причина последующего, причем с описанием этих событий в пространстве и во времени: …→N→причина роста→прирост ΔN за Δt→N + ΔN→…
В этом, и только в этом случае, закон квадратичного роста dN/dt = N2/C может рассматриваться как причинный закон, описывающий автокаталитический, самоускоряющийся процесс, как положительная обратная связь второго порядка. Рост численности любых размножающихся «частиц», происходящий в соответствии с таким причинным законом квадратичного роста, может служить примером режима с обострением.
Режим с обострением – это такая стадия развития динамического процесса, которая описывается причинным законом, задающим нелинейную положительную обратную связь (НПОС), в результате непрерывного действия которой одна или несколько моделируемых величин обращается в бесконечность за конечный промежуток времени.
* * *Закон роста населения Земли в Википедии до 2014 года описывался как режим с обострением со ссылкой на работы А.В. Коротаева, пока я не удалил это физикалистское его описание и не дал правильное определение этому закону.
На той же странице Википедии (2016 г.), где дано определение режима с обострением, в списке литературы до сих пор указаны работы, в которых описывается гиперболический рост, не являющийся режимом с обострением. Это книга А.В. Коротаева и соавторов по гиперболическому росту населения Земли: «Законы истории…» 2-е изд. М.: УРСС, 2007. И статья А.В. Маркова и А.В. Коротаева: «Динамика разнообразия фанерозойских морских животных соответствует модели гиперболического роста» Журнал общей биологии. 2007, № 1.
Кто бы вычистил Википедию от сочинений и ссылок на «труды» этой сладкой парочки, представляющей результаты своих более чем сомнительных исследований по гиперболическому росту как окончательные и бесспорные. А ведь именно таковыми должны быть статьи в Википедии: окончательными, бесповоротными, бесспорными, как формула Эйнштейна E = mc2. Эти же двое не потрудились даже провести каузальный анализ исследуемых закономерностей. Автокаталитичность роста подразумевается ими по умолчанию!
На самом деле никакой ПОС второго порядка между численностью населения мира и скоростью ее роста никогда не существовало. Гиперболический рост числа родов фанерозойских морских животных также не мог происходить по причине ПОС второго порядка, неизменной в течение сотен миллионов (!) лет.
Во всяком случае, это нужно как-то доказывать. Так что Марков и Коротаев, очевидно, поспешили «увековечить» свои имена как имена исследователей гиперболического роста, поскольку так и не поняли причин, вызывающих такой рост.
По тем же соображениям (отсутствие ПОС) неправильно говорить про обострение по скорости в релятивистском законе, описывающем неограниченное возрастание массы тела при росте его скорости. Нет также никакого обострения по времени в законе гиперболического роста населения Земли N = C/(t0– t).
Во всех этих случаях мы имеем дело с функциональной, непричинной связью между переменной и ее приращением, а не с причинным законом, описывающим самоускоряющийся (автокаталитический) процесс.
Миф о том, что население Земли не росло по закону гиперболы
Неспособность объяснить парадоксальный гиперболический рост населения Земли привела некоторых российских ученых к отрицанию самого факта такого роста. Так, С.В. Цирель утверждает, что показатель степенной функции в формуле Фёрстера «необязательно равен единице и необязательно неизменен в течение всей истории человечества»[157]. (См. «Двойной обман С.В. Циреля».)
Выдающийся советский и российский демограф и экономист А.Г. Вишневский написал статью «Демографический переход и гипотеза гиперболического роста населения», в которой поставил под сомнение исследования Фёрстера и других ученых[159]. В этой статье он критикует трактовку демографического перехода сторонниками, как он пишет, гипотезы гиперболического роста. А.Г. Вишневский считает, что С.П. Капица умножал сущности без надобности, усложнял и мистифицировал картину роста населения Земли. Особой критике он подверг главный принцип теории Капицы: принцип демографического императива, согласно которому рост человечества никогда не зависел ни от каких ресурсов[160].
Доктор биологических наук Николай Векшин (а еще он поэт, писатель и бард!) опубликовал сборник «Переосмысление перманентных парадигм», в котором есть статья «Гиперболический казус Капицы»[168]. В этой статье он высказывается в негативном ключе в адрес теорий гиперболического роста населения мира.
Сборник Векшина читается легко и с большим удовольствием, но с заметками по теории Капицы, СТО и некоторыми другими согласиться невозможно. Здесь мы имеем дело с тем случаем, когда мыслящий и, безусловно, талантливый человек пытается судить о предмете, далеком от его деятельности, не и имея о нем достаточно полной информации. Приведем некоторые выдержки из этой статьи с нашими комментариями:
«Вопреки этому, в книге Капицы „Парадоксы роста: Законы развития человечества“ (М., 2010) говорится именно о гиперболическом росте населения Земли за последние 4000 лет[169]. Почему за 4000 лет? Во-первых, для более древних времен практически нет данных. И, во-вторых, при экстраполяции, например, на 8000 лет функция Капицы устремляется в нуль[170]. А это вступает в противоречие с общепринятым мнением, что история человечества насчитывает примерно 100 тысяч лет.
Но что касается точных цифр, необходимых для построения именно гиперболы, а не экспоненты или иной резкой функции, то для всей многотысячелетней истории человечества существует большая неопределенность[171]» «…»
«В книге Капицы приведена формула N = 200 x 109/(2025 – T). Откуда взялась цифра 2025? Она была «угадана» Капицей[172], а все исходные цифры «округлены и поправлены» так, чтобы при экстраполяции с использованием гиперболической функции получить именно это число[173]. Гиперболическая функция весьма крутая, поэтому малейшие неточности в данных о народонаселении в течение веков должны дать колоссальную неопределенность в прогнозе[174]. Капица это проигнорировал. По Капице, 2025 год это демографический Апокалипсис[175]. Сразу после 2025 года функция уходит на бесконечность[176]. Абсурд» «…»
«Вообще в разных странах в одно и то же время рост населения ведет себя абсолютно по-разному и описывается совершенно разными математическими функциями. Капица же берёт некую «среднюю по планете» функцию[177]. Это как в анекдоте про «среднюю температуру по палате». Почему Капица предсказал Апокалипсис именно на 2025-й год? Потому что 2010-й год прошел, не вызвав Апокалипсиса[178]. Таким образом, гиперболическая модель С.П.Капицы не более, чем псевдонаучный казус[179]».
В.Г. Кононов в статье «Мистика и истина гиперболического закона» пишет о том, что результаты, полученные классиками закона гиперболического роста основаны почти исключительно на оценках за 1650—1970 гг. Именно в это время, по его мнению, «рост численности человечества был наиболее жестко связан с определяющим влиянием фундаментальных процессов накопления информации, под которые подстраивались все прочие процессы человеческого развития». В другие периоды динамика численности населения, как он считает, подчинялась другим законам[162].
В статье «О гиперболическом росте человечества» Д.Г. Егоров, М.А. Манойлова и К.В. Селезнёв пришли к выводу, что «эмпирическая зависимость фон Фёрстера является гипотезой, в сущности, не имеющей убедительного эмпирического обоснования»[167][166].
Здесь мы попытаемся убедить читателя в ошибочности подобных представлений. Прежде всего, зададимся вопросом: что значит утверждение о том, что рост населения был гиперболическим? Ясно, что реальная кривая роста населения Земли не была гладкой и монотонной со всеми своими производными функцией и что на ней присутствует множество «выбоин и зазубрин». Понятно, что первая производная от численности по времени или скорость роста на всем протяжении эволюции человека испытывала множество взлетов и падений. Ясно также, что данные по численности имеют значительную погрешность и она растет по мере удаления в прошлое.
Но когда встает вопрос о том, по какому закону росло человечество последние несколько сотен лет, нужно подобрать гладкую, монотонно возрастающую на выбранном интервале исторического времени функцию, наилучшим образом отвечающую известным демографическим данным. Необходимо выбрать один из нескольких известных законов роста, уравнение которого задает эту функцию, если, конечно, такой закон существует и рост населения мира не представлял собой чисто стохастический процесс.
Про этот закон можно сказать следующее: он должен быть известным и простым по форме, должен описывать на выбранном промежутке неограниченный монотонный рост и, кроме того, у функции, определяющей этот рост, как и у сглаженной эмпирической зависимости численности населения Земли от времени, должна быть положительная кривизна.
Таким образом, исключаются все законы немонотонного роста такие, как циклический рост, законы ограниченного роста – такие, как логистический рост; а из законов монотонного роста следует исключить логарифмический, а также степенной рост с отрицательной или равной нулю кривизной N(t): dN/dt = αNp (p ≤ 0). Остаются, если говорить о наиболее известных простых законах неограниченного роста, законы степенного роста (dN/dt = αNp): параболический (0 < p < 1), экспоненциальный (p = 1) и гиперболический (p > 1). Этим данный список, конечно, не ограничивается: сюда могут быть добавлены некоторые другие элементарные функции и их комбинации. Но наиболее часто встречающиеся законы роста, удовлетворяющие обозначенным условиям, – это экспоненциальный (p = 1), параболический (p = 1/2) и гиперболический (p = 2).
Простота закона выражается в том, что уравнение, описывающее такой закон, содержит минимальное число постоянных, определяющих рост. Следовательно, дифференциальное уравнение этого закона должно быть первого порядка, а его решения зависеть от двух параметров: константы роста и начального условия, точнее, фиксированного значения численности в некоторый заданный момент времени. Константа роста – это системный инвариант и у каждого закона роста она своя.
Поясним это на примерах. Закон экспоненциального роста описывается уравнением dN/dt = αN и его решение N = N0eαt определяется значением численности в некоторый начальный момент времени N0 и постоянной роста α, обратная от которой 1/α – время, за которое численность возрастает в 2,7 раза. Это время и есть системный инвариант экспоненциального роста, т. к. не зависит от численности и остается неизменным в его процессе.
Инвариантом линейного роста является скорость, параболического – ускорение роста численности. Инвариантом гиперболического роста, по закону которого росла численность населения Земли, является постоянная Фёрстера: произведение численности N(t) в любой момент времени t на время tс − t, оставшееся до наступления сингулярности.
Чтобы проверить был ли рост численности населения мира гиперболическим последние две тысячи лет используем данные по росту населения Земли, взятые из наиболее известных и надежных источников [40]. По методу наименьших квадратов найдем гиперболу, наилучшим образом отвечающую этим данным. Приведенный инвариант роста определим как произведение численности N(t) в момент времени t на время до сингулярности t − tс, поделенное на постоянную Фёрстера C (tс = 2022 год, C = 189 млрд лет).
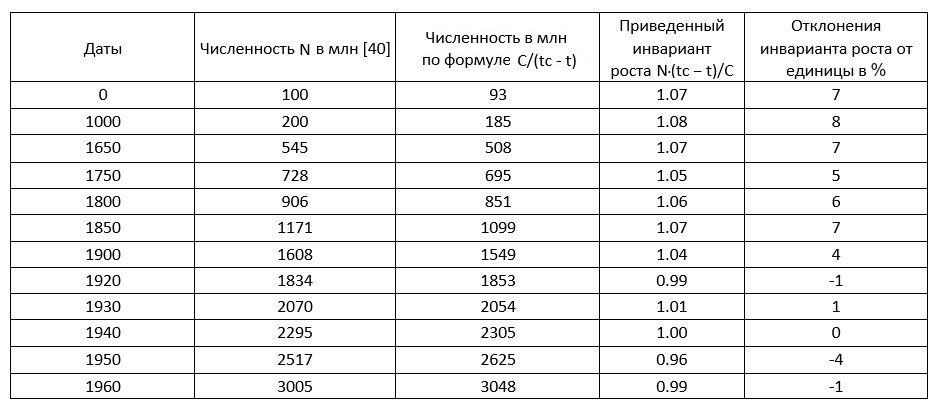
Таблица 1. Подсчет приведенного инварианта роста за последние две тысячи лет по данным, представленным в работе Остина и Брюэра [40] ( tс = 2022, C = 189 млрд).
Из таблицы 1 видно, что отклонения приведенного инварианта роста от единицы за последние две тысячи лет не превосходят восьми процентов. Следовательно, можно говорить о том, что рост населения Земли от начала новой эры до шестидесятого года прошлого столетия с хорошей точностью был гиперболическим.
Но может быть можно подобрать какую-нибудь другую простую функцию, моделирующую рост населения мира с такой же, или даже с лучшей точностью? Возьмем наиболее простой закон роста dN/dt = αNp и определим по методу наименьших квадратов экспоненту (p = 1), квадратичную параболу (p = 1/2) и «школьную» гиперболу (p = 2), наилучшим образом отвечающие демографическим данным (таб. 1) за последние триста лет, и сравним их между собой[180]. Результат представлен на рисунке 1.
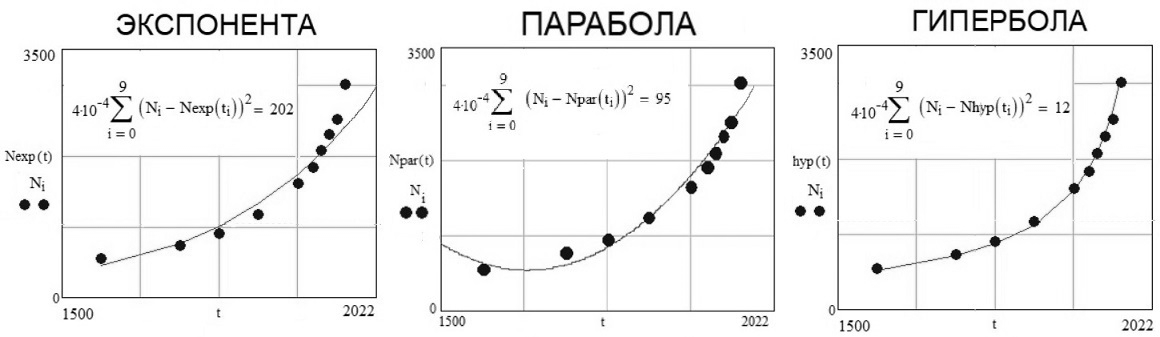
Рис. 2. Экспонента, парабола и гипербола, наилучшим образом отвечающие данным по населению мира за последние триста лет. [40]
Из приведенных графиков видно, что экспоненциальный закон не может обеспечить необходимую скорость роста на заключительном его этапе. Параболический закон делает это гораздо лучше. Но наилучший результат у гиперболы Фёрстера N(t) = 189/(2022 − t) млрд: все точки, отвечающие демографическим данным, практически точно лежат на графике. Об этом говорит и сумма квадратов отклонений теоретической кривой от демографических данных: у гиперболы она гораздо меньше, чем у экспоненты и параболы[181]. Возможно, кто-то поставит под сомнение данные по численности, взятые из работы [40]. Так, А.Г. Вишневский пишет:
«… А. Подлазов и другие сторонники теории гиперболического роста, строя свои модели, имеют дело не с реальными эмпирическими данными, а с квазиэмпирической моделью, построенной другими исследователями, и оценивают успешность своих модельных построений, исходя из того, насколько построенные ими графики соответствуют тому, что они называют реальными данными, но что, на самом деле, таковыми не является». «…»
«Объединение и усреднение всех имеющихся приблизительных оценок [Goldewijk etal. 2010; HYDE 2011] позволяет построить усредненную кривую численности мирового населения за всю историю его существования (рис. 1), но изначально ясно, что это приблизительная, идеализированная, сглаженная кривая, такая идеализация заложена в самой процедуре оценок[163]. Имея крайне ограниченную и ненадежную информацию о реальных величинах[164], авторы оценок должны были стремиться к их правдоподобию и сообразовывать их со своими самыми общими априорными представлениями об исторической динамике мирового населения[165]».
Д.Г. Егоров, М.А. Манойлова и К.В.Селезнёв[166] выражают сомнение в достоверности данных по численности населения мира, использованных Фёрстером и его последователями, и считают, что «если какие-то данные укладываются на графике вблизи какой-то кривой (описываемой какой-либо математической формулой), это зачастую означает просто совпадение, более–менее случайное».
Но усредненные данные по одиннадцати независимым бюро населения в таблице 2 и на рисунке 2 однозначно указывают на гиперболическую зависимость (данные и ссылки на источники можно найти здесь[182]). О какой тогда ненадежности данных, и о каком тогда случайном совпадении может идти речь?
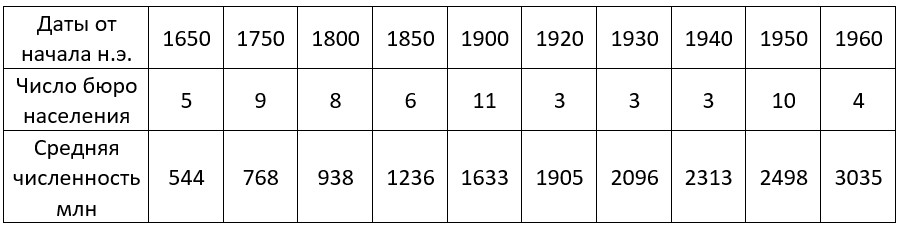
Таблица 2. Усредненные данные по численности населения Земли в млн по разным бюро населения[182].
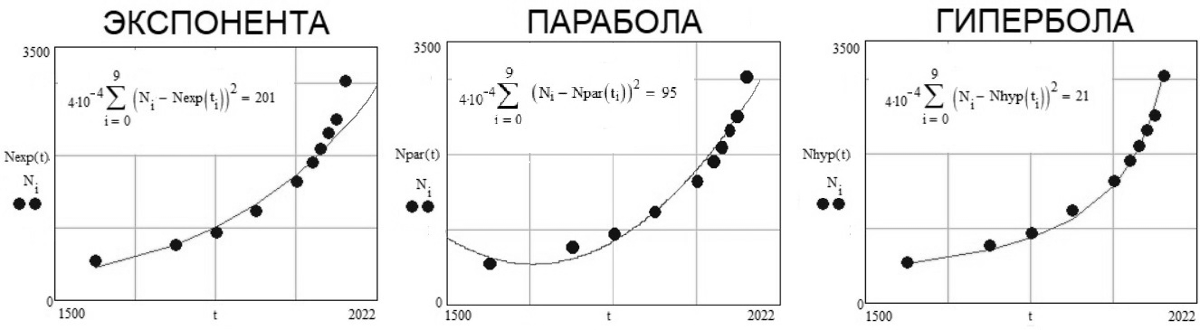
Рис. 3. Экспонента, парабола и гипербола, наилучшим образом отвечающие усредненным данным по населению мира за последние триста лет, взятым из разных источников.
Необходимо отметить следующее: квадратичная парабола, т. е. полином второй степени, полностью определяется тремя параметрами и поэтому ею обычно проще интерполировать данные, чем экспонентой или «школьной» гиперболой, у которых таких констант только две. Если же взять полином третьей степени – можно еще больше уменьшить сумму квадратов отклонений (24), но только полином четвертой степени даст лучший результат (7), чем у гиперболы.



