Население Земли как растущая иерархическая сеть

В наше время большое значение имеет прогресс в области общественного здравоохранения, санитарии и гигиены, повышение доступности продовольствия, расширения и развития торговли и транспорта, введение в эксплуатацию новых источников энергии, комплекс мер, направленных на борьбу с пьянством, алкоголизмом и наркоманией, успехи геронтологии, снижение детской смертности и т. д., и т. п. Ясно, что список этот не имеет конца.

Рост популяции микроорганизмов, размножающихся делением, в каждый момент времени определяется ее полной численностью. То же можно сказать и о человеческой «популяции»: численность – это главный показатель роста и растет она по причине полового размножения. Для популяции животных главную роль здесь играет количество половозрелых самок. Для человеческого общества все неизмеримо сложнее.

Составляющая естественного прироста за счет рождаемости значительно меньше полной численности. Она не возникает из ниоткуда, а появляется в результате, если можно так выразиться, «репликации» некоторых из живущих особей. Этим процесс роста численности людей отличается, например, от процесса размножения нейтронов в цепной ядерной  реакции. И именно поэтому естественный прирост есть небольшое приращение, зависящее, прежде всего, от общего числа живущих.

Модели первого типа можно считать однофакторными или однопричинными. Из множества всех существующих причин роста в каждой такой модели выделяется по тому или иному признаку подмножество, которое объявляется главной, доминирующей причиной прироста, а остальными причинами – пренебрегается.

Так, в мальтузианских моделях, где главная причина роста – это ресурсы, они и объявляются его единственной причиной. При этом считается, что выделенная моделью причина воздействуют не на отдельные страны и народы, а на все человечество в целом. Т. е. закон роста представляет собой зависимость между численностью всего человечества и какими-то другими переменными.

В моделях первого типа эта зависимость выражается в форме дифференциального уравнения или системы уравнений, связывающих (причем связь эта причинно-следственная) скорость роста с численностью. (Годовой мировой естественный прирост равен скорости роста численности.)

Если скорость роста пропорциональна численности – рост будет экспоненциальным. Если же она пропорциональна квадрату численности (такая зависимость называется законом квадратичного роста) – рост будет гиперболическим.

Рис. 1. Закон квадратичного роста. Скорость роста численности населения мира пропорциональна квадрату численности.

Решения уравнения или системы в однопричинной модели определяются начальными условиями. Одним из таких решений, удовлетворяющим условию N(t0) = N0, будет теоретическая гипербола. И здесь должно быть полное согласие теории и «эксперимента»: теоретической гиперболы и гиперболы Фёрстера.

Почти все существующие теории роста населения Земли – теории первого типа. Рост численности здесь полностью определяется законом квадратичного роста. Т. е. считается, что опосредованная причинная связь между естественным приростом и численностью, механизм которой для каждой модели свой, является главной, доминирующей и достаточной для объяснения роста.

* * *

Второй тип – это модели, математический аппарат которых нелинейные дифференциальные или функционально-дифференциальные уравнения в частных производных, причем во втором случае составленные с учетом не только настоящего состояния объекта, но и всей его предыстории. В таких моделях должна исследоваться динамика роста популяции не только во времени, но и в пространстве, учитываться продолжительность жизни, показатель фертильности, какие-то другие переменные.

Главное отличие моделей второго типа от первого, где человечество единая, однородная, неделимая система в том, что здесь эта система сначала разбивается на некоторое число частей или подсистем, различающихся по тем или иным признакам, и исследуется рост и развитие каждой из таких частей в отдельности. И лишь затем численность народонаселения каждой такой части суммируется с другими частями, в результате чего и получается теоретическая зависимость численности населения мира от времени.

Что гораздо лучше соответствует действительности, т. к. парадоксальная системность человечества, необходимая для построения любой модели первого типа, представляется совершенно невероятной. Гиперболический рост населения Земли в таких синергетических моделях, если они когда-нибудь будут построены, будет описываться как режим с обострением.

Режим с обострением – это такой закон роста, при котором одна или несколько моделируемых величин обращаются в бесконечность за конечный промежуток времени. Формируется в результате действия механизма нелинейной положительной обратной связи.

Численность населения мира будет здесь ведущей переменной и после упрощающих предположений, в асимптотике, по мнению тех, кто считает, что гиперболический рост может быть объяснен на основе синергетики, должен проявиться удивительный по своей простоте закон, открытый Фёрстером. (Модели второго типа должны также объяснить явление сжатия исторического времени: исторические циклы, длительность которых сокращается по закону прогрессии, о существовании которых писал историк И.М. Дьяконов.)

При этом предполагается, что рост хотя и идет по случайной гиперболе, должен существовать механизм устойчивости, который каким-то образом возвращает ведущую переменную на изначальную кривую или, по крайней мере, не слишком далеко от нее уводит. Ни одна из попыток построить модель второго типа так и не увенчалась успехом. См., например, [23]. Есть и откровенная подгонка под результаты феноменологической теории Капицы, авторы:  Е.Н. Князева, В.А. Белавин, Е.С. Куркина, которая никак не может считаться адекватной моделью второго типа[146].

Вероятно, подход к этой проблеме на основе теории самоорганизации с использованием методов синергетики является предвзятым и неверным в принципе [151]. В любом случае множество моделей второго типа остается пока пустым.

* * *

Модели третьего типа основаны на телеологической детерминации или постдетерминации. Такой тип детерминации предполагает наличие у процесса, в данном случае процесса роста численности населения мира, какой-то цели. Этот рост численности считается важнейшим, если не главным фактором, определяющим рост и развитие ноосферы, высшей стадии эволюции биосферы.

Существует ли ноосфера как система в том смысле, в каком существует Гея Лавлока? Применимы ли к ней законы нижних уровней? А может быть так же, как в концепции Геи, в ее «сильном», телеологическом варианте ноосфера как самодетерминирующаяся, причинно-активная система определяет не только свою структуру, но и направление собственной эволюции?

Любая модель третьего типа формально может быть сведена к модели, аналогичной модели  первого типа с преддетерминацией, если считать рост многофакторным или многопричинным.

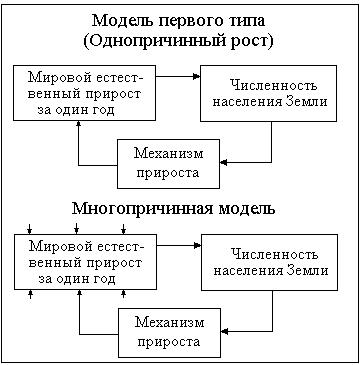
Рис. 2. Причинно-следственная диаграмма однопричинной и многопричинной модели роста.

В случае многопричинной модели естественный прирост также определяется, прежде всего, общей численностью, но в отличие от однопричинного варианта на него могут влиять абсолютно все возможные и, вообще говоря, случайные причины; случайные лишь в системе координат, связанной с процессами, протекающими внутри мировой демографической системы.

При наличии же внешней управляющей системы (реальной или виртуальной) множество причин, влияющих на рост, можно разбить на два подмножества: действительно случайные причины и причины, лишь кажущиеся случайными, а на самом деле направляющие рост на гиперболу Фёрстера. Т. е. здесь мы имеем дело с управляемым случайным процессом. (Возможна такая аналогия: переход парусного судна из одного порта в другой, происходящий в условиях случайно меняющихся по направлению и скорости атмосферных течений. Управляющей системой здесь служат штурман и капитан.)

Иначе говоря, множество этих причин будет максимально по́лно и никак не структурировано. Причем все они необязательно должны быть связаны с общим числом живущих. Такой подход хорошо согласуется с представлением о том, что человечество никогда не было единым информационным полем и не представляло собой системы, способной обеспечить гиперболический рост своей численности.

Оно всегда, особенно в прошедшие исторические эпохи, было разобщено, прежде всего, территориально, и рост каждого этноса, народа происходил в основном независимо от других. А естественный прирост каждой составляющей человечества как системы, т. е. каждого этноса, народа, страны (другого подмножества, выделенного по принципу общности какого-либо из его свойств) не зависел совсем или зависел слабо от общей численности населения Земли и определялся, прежде всего, своими собственными причинами.

При этом в сумме общее число живущих на интервалах, длительность которых превышает продолжительность человеческой жизни, росло по гиперболическому закону.

Существует единственная модель третьего типа, в которой гиперболический рост и глобальный демографический переход объясняются эквифинальностью главного цикла эволюции человека и истории человеческого социума, порождающего Кондратьевский цикл. Ниже мы рассмотрим ее в качестве примера модели роста, основанной на целевой постдетерминации.

* * *

Закон гиперболического роста удивительно прост и потому даже сложная модель второго типа обязана иметь асимптотическое решение в виде модели первого или третьего типа. И модель эта должна быть либо однопричинной, либо многопричинной — третьего не дано.

Парадокс заключается в том, что выбор здесь происходит между невероятным и невозможным. Дилеммы можно избежать, если вообще отрицать факт гиперболического роста численности населения мира. И считать, что рост был экспоненциальным или несколько более крутым — «надэкспоненциальным». Как ни странно, такой позиции до сих придерживаются многие демографы и не только демографы, но и другие ученые, представители смежных наук[152].

Одни вообще ничего не слышали про гиперболический рост, другие считают исследование Фёрстера и его коллег ошибочным, третьи пытаются объяснить рост населения Земли на основе теории Мальтуса. Рост численности по экспоненте полностью отвечает существующей на данный момент научной парадигме, в то время как признание его гиперболическим требует, по-видимому, коренной ее ломки.

 Есть еще одна возможность избавиться от неудобного, никак не вписывающегося в существующую парадигму закона Фёрстера: исказить его. Эту возможность использует историк-востоковед А.В. Коротаев, подменяя в своих работах понятие «закон гиперболического роста», подразумевающее точность, значимость и незыблемость на понятие «гиперболический тренд» (текущая тенденция), которое ассоциируется с непостоянством и неустойчивостью.

Соавтор Коротаева по ряду работ, С.В. Цирель, идет другим путем: им совершенно бездоказательно утверждается, что население мира росло по закону гиперболы лишь в XVIII–XX веках, т. е. только последние три столетия.

Сколь бы странным это ни показалось, но, возможно, незнание, отрицание или даже искажение открытия Фёрстера и есть наилучший на данный момент выбор. Во всяком случае – это лучше, чем выбирать между невероятным и невозможным.

* * *

Все существующие однопричинные модели гиперболического роста имеют целый букет врожденных пороков. Это и неизменный в течение тысячелетий закон роста, это и непонятная системность человечества, связанная с простотой и нелинейностью уравнения (1), это и парадоксальная, необъяснимая законом dN/dt = N2/C устойчивость роста. Кроме того, все они построены практически по одной и той же схеме.

Все авторы, кроме С.П. Капицы, на основании соединительных (конъюнктивных) суждений типа: А~В∩А~С → А~В*С или с использованием силлогизма получают дифференциальную форму dN/dt = N2/C или несколько более сложную, которую и объявляют причинным законом роста численности человечества. Поверить в то, что одна из множества таких противоречивых, умозрительных, ничем не подтвержденных моделей может объяснить гиперболический рост – значит поверить в невозможное.

Все модели первого типа можно разбить на три класса:

1. К первому следует отнести те из них, в которых предлагается не только конкретный механизм реализации закона квадратичного роста dN/dt = N2/C или какого-либо другого более сложного причинного дифференциального закона, описывающего рост, но и способ его реализации. А также поднимается проблема устойчивости роста, без решения которой подобные построения лишены всякого смысла.

2. Ко второму классу относятся модели, в которых рассматривается конкретный механизм реализации закона dN/dt = N2/C, но не делается никаких серьезных попыток понять как такой механизм мог привести к гиперболическому росту населения мира. Проблема устойчивости роста в них игнорируется.

3. В моделях третьего класса нет, по сути, ничего кроме математических уравнений, т. е. это голая математика (где нет решения проблемы устойчивости роста), единственное назначение которой дать полное согласие с «экспериментальными данными», т. е. с гиперболой Фёрстера.

К первому классу относится теория Капицы. Автор предлагает модель коллективного взаимодействия; разрабатывается, а затем отвергается целый ряд чисто умозрительных способов ее реализации.

Сначала рассматривается «модель взаимодействия городов»: населенных пунктов с численностью K = 67 тыс. человек, затем модель распространения информации по схеме цепной реакции, и, наконец, в качестве причины, способной объяснить парадоксальную системность человечества, предлагается нелокальное (!) взаимодействие.

Автор честно отмечает нерешенность проблемы устойчивости роста в рамках своей модели. (В последней своей работе [21] С.П. Капица приходит к выводу, что причину аномального гиперболического роста искать вообще не нужно: вполне достаточно его «феноменологии»…)

Модель Коротаева служит хорошим примером гипотезы, в которой предлагается конкретный механизм роста, но не делается никаких серьезных попыток понять, как такой механизм мог работать в пространстве и во времени на территории Мир-системы.

И, наконец, последний член этого ряда – модели полностью оторванные от реальности и представляющие собой, по сути, какие-то бессмысленные математические игры. Примером такого «творчества» может служить работа С.В. Циреля[153], в которой гиперболический рост населения Земли представляется переходным между нулевым и экспоненциальным.

* * *

В многопричинной модели причины роста меняются со временем, они различны для разных стран, народов и регионов, численность населения которых в сумме составляет численность человечества. При этом считается, что рост населения мира процесс хотя и случайный, но направленный к определенной цели и на временах бо́льших, чем некоторое характерное время является гиперболическим.

Такое свойство растущей системы «все человечество в целом» достигать в реперных точках своего роста предустановленных значений численности и следовать во все времена одной и той же гиперболе демографического роста называется эквифинальностью. Именно оно обеспечивает выполнение в среднем закона квадратичного роста, который причинным законом в многопричинной модели уже не является, а представляет собой сопутствующую, непричинную (не ПОС) связь между численностью и скоростью ее роста.

Многопричинная модель равносильна модели третьего типа с постдетерминацией и поверить в такой механизм гиперболического роста, противоречащий всем существующим представлениям о росте численности популяции, – значит поверить в невероятное.

Причинные и непричинные законы

Для дальнейшего нам понадобится классификация законов по способу их детерминации. Законы по типу детерминации подразделяются на причинные и непричинные. Существуют два типа причинных (каузальных) законов: с преддетерминацией, когда время детерминации некоторого события предшествует времени его наступления, и с постдетерминацией, когда момент детерминации расположен позднее того момента времени, в который происходит это событие.

Во многих контекстах причинный закон отождествляется с законом, основанном на преддетерминации. Вместе с тем понятие закона с постдетерминацией, которая может быть также названа телеологической или целевой детерминацией, необходимо при описании целого ряда биологических, экономических, социальных, кибернетических объектов и систем.

Как причинные, так и непричинные законы можно разделить на функциональные законы и законы корреляции. Функциональный закон вне зависимости от его каузальной интерпретации определим здесь как такой закон, который описывает связь, при которой каждому значению одной переменной, входящей в уравнение закона, соответствует одно или несколько строго определенных значений другой.

Это определение отличается от часто встречающегося определения, отождествляющего по способу детерминации функциональную связь с сопутствующей. Дело в том, что важную для данного изложения связь между скоростью роста и численностью в уравнении dN/dt = N2/C всегда можно назвать по форме функциональной, а по способу детерминации – причинной или непричинной (сопутствующей).

Корреляционный закон – это такой закон, при котором с изменением переменной X меняется и переменная Y, но каждому значению X могут соответствовать разные, заранее непредсказуемые значения Y, и наоборот. Корреляционный закон описывает на языке теории вероятностей коррелятивную связь между явлениями или процессами, причем в отличие от функционального закона, связь эта остается целиком или частично невыясненной.

Причинный закон описывает причинно-следственную (каузальную) связь. Непричинный закон выражает непричинную коррелятивную или непричинную функциональную связь. Если наступление события А увеличивает вероятность наступления события В, то между ними существует причинно-следственная (причинная, каузальная) связь.

Определение причинного закона дает Бертран Рассел в своей книге «Человеческое познание, его сферы и границы»:

«Причинный закон, как я буду употреблять этот термин, может быть определен как главный принцип, в силу которого – если имеются достаточные данные об определенной области пространства-времени – можно сделать какой-то вывод об определенной другой области пространства-времени» [44].

Сопутствующая связь – это вид коррелятивной непричинной или функциональной непричинной связи, при которой изменение одного из связанных объектов сопутствует во времени изменению другого. Именно сопутствует, сопровождается, а не «причиняется». Сопутствующая связь – это связь сосуществования и одновременности. Это связь синхронных, в первом приближении не взаимодействующих процессов.

Объекты, находящиеся между собой в таком взаимодействии, связаны причинно (каузально) лишь в том смысле, что являются производными одного и того же основания. Т. е. существует общее для них явление-причина.

* * *

Один из способов находить причинные связи – изучение функциональных зависимостей. Так, для понимания причин, вследствие которых изменяется сопротивление проводника, оказалось достаточным найти функциональную зависимость между проводимостью и температурой. В непричинной связи объектов отсутствуют как таковые главные признаки причинно-следственной связи: производительность (объекты не производят друг друга), асимметричность во времени (они сосуществуют равноправно, симметрично во времени), необратимость.

В случае сопутствующей связи часто имеет место обратимость, т. е. возможность перестановки местами независимых переменных. Функциональный (не каузальный) подход особенно важен, когда предметом изучения являются процессы, внутренний причинный механизм которых пока неизвестен и выступает как своего рода черный ящик.

Примеры:

A. Свободно падающее тело: связь между мгновенным значением скорости и пройденным путем. Связь причинная, асимметричная S → V.

B. Связь между шириной зоны разброса дроби и расстоянием до цели: связь функциональная, сопутствующая; позволяет определять это расстояние по результатам исследования мишени.

C. Связь между энергопотреблением и численностью. Мировое энергопотребление в эпоху гиперболического роста пропорционально квадрату численности населения мира, но рост численности не есть причина роста энергопотребления. А рост энергопотребления не есть причина роста численности. Процессы эти сопутствующие и связь между ними сопутствующая (в первом приближении, т. к. эти явления – высшей степени сложности), а не причинно-следственная. Такая же связь, как мы покажем далее, существует между численностью населения мира и скоростью ее роста (годовым естественным приростом).

* * *

Когда мы хотим объяснить какое-то явление, нам приходится ставить вопрос о его причине и искать причинно-следственную, каузальную связь. Проблема анализа причинности – одна из вечных проблем философии, которой философы занимаются на протяжении тысячелетий. Ею интересовался еще Аристотель, а статьи, посвященные причинности, до сих пор можно встретить на страницах современных философских журналов.

Хотя понятия причина и следствие обычно относятся к событиям, происходящим в пространственно-временном континууме, понятие событие в каузальном анализе можно заменить на понятие процесс, свойство, переменную. В точных науках исследуется связь между переменными, входящими в математическую зависимость, выражающую некоторый закон. Рассмотрим две переменные, описывающие некоторые свойства системы как функции времени: x(t) и y(t). Про связь между этими переменными y(x) можно сказать следующее:

1. Во-первых, она может вообще отсутствовать – тогда справедлива нулевая гипотеза.

2. Во-вторых, она может быть коррелятивной, когда наличие взаимозависимости между переменными не вызывает сомнений, но природа ее остается неизвестной.

3. В-третьих, связь эта может быть причинно-следственной, когда изменение переменной x(t) есть причина, по которой изменяется переменная y(t) (или наоборот).

4. В-четвертых, связь эта может быть по форме функциональной или коррелятивной, а по способу детерминации – сопутствующей, если существует количественный динамический (статистический) причинный закон с пред или постдетерминацией для каждой из переменных x(t) и y(t), в результате непрерывного действия которого и возникает зависимость между переменными y и x: y(x), которая не является в этом случае причинным законом.

В физике чаще всего исследуется причинно-следственная связь с преддетерминацией между мгновенными значениями переменных. Примером такой связи может служить второй закон Ньютона: a(t) = F(t)/m. Значение ускорения в каждый момент времени равно силе, действующей на тело в этот же момент времени, деленной на его массу. Сила здесь – причина, ускорение – следствие, запаздывания – нет[154].

Можно расширить понятие причинного закона, считая, что «причинная переменная» может быть не только дифференциальным, но и интегральным, «накопленным» во времени показателем, характеризующим динамическую систему.

Так, закон, связывающий мгновенную скорость тела с работой сил на него воздействующих, можно считать причинным законом. В простейшем случае, когда рассматривается движение в однородном силовом поле, можно говорить о причинной связи между пройденным путем и приобретенной телом скоростью. Здесь причинная переменная «накапливается» во времени.

Отметим важный частный случай каузального анализа связи двух динамических переменных x(t) и y(t), когда y(t) = Δx(t) = x(t) – x(t – Δt). Здесь в качестве второй переменной выступает приращение первой за небольшой промежуток времени Δt.

Если переменная x(t) на интервале Δt вызывает свое собственное приращение Δx(t) = f(x)Δt, т. е. является причиной собственного роста (уменьшения), то причинно-следственная связь x(t) <—> Δx(t) называется обратной связью.

Обратная связь может быть определена не только для функционального причинного закона, но и для причинного закона корреляции; она может быть как положительной (ПОС), так и отрицательной (ООС). Важно понимать, что уравнение Δx(t) = f(x)Δt может и не выражать причинный закон, а связь между x(t) и Δx(t) может и не являться ПОС или ООС.

* * *

Приведем примеры. Примером положительной обратной связи может служить связь между численностью популяции и ее естественным приростом. Рассмотрим закон экспоненциального роста популяции: dN/dt = αN. В этом причинном законе причинной, накопленной переменной является численность популяции N, а переменной-следствием – ее прирост dN за некоторый небольшой, фиксированный промежуток времени dt.