Население Земли как растущая иерархическая сеть

При этом принимается на веру, что численность населения Земли всякий раз «мгновенно» выходит на уровень N, как только достигается уровень развития технологий Т, т. е. длительностью «переходного периода» здесь пренебрегается.

Рис. 1. Модель технологического и демографического роста М. Кремера.

На основе этих допущений А.В. Коротаев, А.С. Малков и Д.А. Халтурина составили «компактную» систему уравнений экономического и демографического роста Мир-системы, где в качестве показателя развития ввели объем производства ВВП на душу населения S.

В результате проведенного ими статистического анализа было установлено, что этот показатель пропорционален численности населения Земли: S = kN. Считая эту связь причинным законом в тенденции: рост численности N вызывает рост объема ВВП на душу населения S (на самом деле связь эта сопутствующая, и мы в дальнейшем это докажем[186]), авторы «выводят» основной закон роста населения Земли – закон квадратичного роста.

* * *

Мальтузианско-кузнецианская теория Коротаева и соавторов, основанная на представлении о деятельности мифических изобретателей, вызывающей рост населения мира, не заслуживает никакого доверия, и тому есть целый ряд причин:

1. Число изобретателей и уровень развития жизнесберегающих технологий согласно модели Коротаева пропорциональны численности населения Земли (Ni ~ N, T ~ N). Связь этих величин с численностью считается причинной. Отсюда делается вывод, что скорость технологического роста, так же как и скорость роста численности населения Земли причинно пропорциональны квадрату численности (dN/dt ~ N2).

Такие допущения считаются если не очевидными, то вполне правдоподобными и принимаются на веру без доказательства как постулат. Но можно ли в них поверить, ведь постулируется сразу три глобальных причинных закона. Не слишком ли много?

И, кроме того, для их выполнения требуется быстрое распространение изобретений на всю Ойкумену, т. е. единое для всего населения мира информационное поле. Иначе говоря, миф об изобретателях не может существовать без мифа о Мир-системе. На шатком основании выстраивается не менее шаткая надстройка. Т. е. здесь мы имеем дело с мифом в квадрате.

2. Функция распределения множества изобретений по значимости не является равномерной, что противоречит основной предпосылке модели Коротаева об изобретателях и изобретениях. Действительно, изобретательская теория Коротаева предполагает большое количество незначительных изобретений.

На самом же деле главную роль в развитии играют не множественные мелкие изобретения, а немногочисленные крупные открытия, «базисные инновации» (по Л. Нефедову), которые в течение десятилетий после их внедрения играют роль локомотива мировой экономики.

3. Важным допущением модели Коротаева является предположение «больше людей – больше (во столько же раз) изобретателей». Но почему при удвоении численности населения мира число изобретателей также удваивается? – Ведь Мир-система не остается подобной себе до такого удвоения, она изменяется и изменяется при этом качественно: растет продолжительность жизни, общественное благосостояние, процент грамотных людей, меняется возрастной, гендерный состав населения…

Почему тогда процент потенциальных изобретателей, присутствующий в формуле Кремера, остается неизменным? По мере роста уровня благосостояния у все большего числа людей, способных к творчеству, высвобождается свободное время, которое они могут потратить на изобретательскую деятельность.

Следовательно, процент таких людей, потенциальных изобретателей, пропорционален ВВП, приходящемуся на душу населения. Во всяком случае, это кажется вполне правдоподобным. К такому же заключению приводит правдоподобное предположение о том, что процент людей, занимающихся изобретательством, пропорционален не полной численности населения мира, а числу грамотных людей, т. к. неуч − плохой изобретатель.

Но число грамотных людей, так же как и ВВП, приходящийся на душу населения, росли по закону квадратичной C'/(t0 – t)2, а не простой гиперболы C/(t0 – t), что, кстати, отмечено и самим Коротаевым [20], т. е. эти величины не были просто пропорциональны численности населения мира, а были (в первом приближении) пропорциональны квадрату этой численности.

В таком случае гипотеза Кремера приводит к противоречию: скорость роста численности населения мира пропорциональна кубу этой численности. Иначе говоря, предположение Коротаева о том, что число изобретателей пропорционально численности населения Земли выглядит как подгонка к закону квадратичного роста.

4. Мальтузианское допущение Кремера о том, что рост численности человечества для каждого момента времени в прошлом был ограничен потолком несущей способности Земли, обусловленным уровнем жизнеобеспечивающих технологий, представляется совершенно неприемлемым. С.П. Капица убедительно показал, что рост численности населения мира никогда не зависел ни от каких ресурсов. [1]

5. Уравнение Кремера, на котором построена вся теория Коротаева, выведено в предположении, что численность населения мира каждый раз «мгновенно» вырастает до потолка несущей способности Земли, задаваемого поднявшимся уровнем технологического развития.

На самом же деле, и мы это в дальнейшем обоснуем[187], временем этого переходного процесса, которое мы назвали временем проявления системности, пренебречь нельзя в принципе и уравнение Кремера должно быть уравнением с запаздывающим аргументом. Если бы время запаздывания было значительно меньше характерного времени исторических изменений, равного примерно сорока годам, эффект был бы незначителен и им можно было бы пренебречь.

На самом же деле на всем пути исторического развития эти времена всегда были как минимум соизмеримы или даже бывали такие периоды, когда время запаздывания значительно превосходило характерное время системы. Динамика роста численности, как показывают исследования таких уравнений с запаздыванием, способна принимать колебательный характер. В такой системе, имеющей петлю обратной связи со столь значительной задержкой, возможны даже резонансы: колебания с нарастающей амплитудой. [24]

Чего ни в малейшей степени не наблюдается: «человеческая популяция» во все времена демонстрировала монотонный, устойчивый гиперболический рост с последующим переходом к стабилизации. Все это говорит о неадекватности изобретательской теории Коротаева.

6. Изобретательская теория Коротаева описывает некий усредненный, «среднестатистический этнос», но почему вообще возможно такое усреднение? Способность к размножению и росту численности у разных народов в разные времена могла отличаться в разы.

Так, до начала глобального демографического перехода коэффициент рождаемости в европейских странах не превосходил 3–4. В наше время, после прохождения ими перехода, он составляет 1.4–1.8, что меньше минимально необходимого 2.11 для простого воспроизводства; при этом происходит вытеснение коренного населения выходцами из стран с исламской культурой, где переход еще не начался и этот коэффициент равен восьми.

7. Точность, которую Фёрстер и его коллеги получили для величин n и t0, обрабатывая большое количество данных за последние две тысячи лет, вступает в противоречие с изобретательской теорией Коротаева.

Можно ли поверить с учетом всего сказанного, что справедливый лишь в тенденции закон квадратичного роста (1), полученный в предположении инновационной природы роста численности, обеспечивает такую фантастическую точность для показателя степенной функции и точки сингулярности гиперболы Фёрстера?

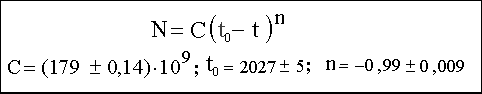
Рис. 2. Результаты обработки Фёрстером демографических данных за две тысячи лет. Точность показателя степенной функции 1 %, точность в определении даты сингулярности 5 лет.

Показатель степенной функции (n = −0.99 ± 0.01) определяет тип степенного закона. Он равен минус единице с точностью до 1 %, т. е. найденная зависимость является самой простой из семейства гиперболических кривых. Именно ее изучают в курсе средней школы. Все это не может быть делом случая. Несомненно, здесь проявилась важная фундаментальная причина, а вовсе не какая-то тенденция, как считает Коротаев.

Как А.В. Коротаев исковеркал «удивительное открытие Хейнца фон Фёрстера»

Поверить в такую фантастическую точность для показателя степенной функции и даты сингулярности, обусловленную лишь изобретательской деятельностью, не просто, что, видимо, понимает и сам Коротаев и поэтому ставит, прежде всего, под сомнение достоверность исследования Фёрстера и его коллег[188].

Но выводы Фёрстера, в том числе те из них, что касаются точности показателя степенной функции, описывающей рост, были подтверждены другими исследователями, в частности, С. Хорнером, а затем и С.П. Капицей, расширившими время действия закона до неолита, а затем и до палеолита.

Но что такое для Коротаева факты, когда теряется правдоподобие его изобретательской теории! И вот вопреки фактам во всех своих публикациях он подменяет понятие «закон», подразумевающее точность, значимость и незыблемость на понятие «тренд» (текущая тенденция), ассоциирующееся с непостоянством и неустойчивостью.

И здесь недостаточно говорить об отсутствии у автора научной честности. Осознанно или нет, Коротаев не только принижает открытие Фёрстера, но и обманывает, вводит в заблуждение читателей своих работ. Кто-то, наверное, скажет: возможно и допустил Коротаев неточность, ведь понятия «тренд» и «закон» близки по смыслу, – стоит ли так придираться?

Но дело в том, что речь-то идет о главном, центральном вопросе исследования, в котором заключена вся суть проблемы, вся ее соль. Что же все-таки открыл Фёрстер? Если это закон, то возникает необходимость объяснять парадоксальную системность человечества, без которой этот закон никогда бы не проявился.

И здесь явно недостаточно мифической Мир-системы Коротаева (которой никогда не существовало в действительности!) и мало рассказать сказку про изобретателей и их матерей. Нужно еще объяснить неизменность закона роста и постоянство постоянной Фёрстера, а также «мистическую» связь между числом рождений и смертей, определяющую «плановое» число живущих.

Нужно объяснить парадоксальную устойчивость гиперболического роста, благодаря которой во все времена, на всех уровнях развития и после любых катастроф закон, управляющий ростом, возвращал этот рост всегда на одну и ту же, по сути, предзаданную гиперболу.

И, наконец, если кривая роста не гипербола, а так, какой-то тренд, то у нее нет особенности и, следовательно, нет никаких связанных с нею проблем. У гиперболы же есть точка сингулярности, и требуются дополнительные усилия, чтобы понять ее смысл.

Но если нет закона, а есть лишь тренд, то все эти проблемы либо полностью снимаются, либо в значительной степени теряют свою остроту. А теперь представим себе читателя, изучающего «труды» Коротаева. Читает он, читает… и доходит до такого места:

«Как было показано нами ранее, именно с развитием Мир-системы связано наличие гиперболического тренда роста численности населения мира» [20] стр.31.

Уравнение гиперболического роста населения Земли не имеет статуса закона, подумает такой читатель. Это всего лишь тренд, а значит, нет и никаких связанных с этим явлением парадоксов. Вот так демистифицирует, а, точнее, коверкает «удивительное открытие Хайнца фон Фёрстера» А.В. Коротаев.

Здесь важно понимать следующее: данные по численности населения Земли, которые по методу наименьших квадратов обрабатывал Фёрстер, представляют собой моментный временной ряд N(t).

Причем период развития, на котором представлен этот ряд, весьма велик: 2000 лет; численность человечества за это время возросла многократно, а Мир-система на всем его протяжении неоднократно претерпевала разнообразные качественные изменения.

В таком случае стандартным подходом представляется разбиение всего этого периода на однородные этапы, в пределах каждого из которых эмпирическая зависимость N(t) подчинялась бы какому-то одному закону развития.

И для каждого такого этапа можно было бы говорить о гиперболическом (линейном, экспоненциальном, логистическом, логарифмическом) тренде роста, справедливом в пределах этого этапа.

Даже если бы такое разбиение было сделано, и на каждом таком этапе мировой естественный прирост оказался пропорционален квадрату численности, а рост был бы, соответственно, гиперболическим, единой гиперболы, гиперболы Фёрстера, как это легко показать, – все равно бы не получилось.

Суть открытия Фёрстера и его коллег как раз и состоит в том, что они такого разбиения не делали, а лишь установили, что все эти данные по населению мира за последние двадцать столетий хорошо соответствуют единой, общей для всех этих данных гиперболе роста. Именно поэтому гипербола Фёрстера – это эмпирический закон роста, и понятие гиперболический тренд, которое по недомыслию ввел Коротаев для показателя N(t), в данном случае – неприменимо.

Так что же все-таки открыл Фёрстер – закон или тренд? Когда в шестидесятом году прошлого века Фёрстер и его коллеги проводили свое исследование в их распоряжении находились данные по переписи населения в разных странах мира за те годы, когда она проводились и данные по численности в исторических документах разной степени надежности.

В своих работах Коротаев акцентирует внимание читателя на том факте, что точность демографических данных падает по мере того, как мы удаляемся в прошлое. Так, если точность, с которой известно число живущих по годам в XX веке составляет единицы процентов, то в XIX веке – это десять процентов, а в начале новой эры – уже десятки процентов.

Отсюда делается вывод׃ т. к. точность данных низка, да еще и падает при уходе в прошлое, то все эти данные в совокупности указывают на то, что гиперболический рост происходил лишь в тенденции, т. е. открытие Фёрстера – всего лишь гиперболический тренд.

Если рассматривать демографические данные, использованные Фёрстером, как результат некоего эксперимента и предположить, что рост численности происходил в соответствии с неким идеальным законом, то отклонение от него имеет две составляющие.

Первая составляющая – это отклонение действительной и неизвестной численности от идеального закона роста, т. е. это ошибка модели. И вторая составляющая – это, собственно, ошибка измерения или ошибка переписи.

Для того, чтобы проявился удивительный по своей простоте закон Фёрстера необходимо следующее: во-первых, растущие по мере удаления в прошлое ошибки демографических данных не должны иметь систематической составляющей. Тогда все они представляют знакопеременный ряд и при их обработке по методу наименьших квадратов имеют тенденцию к взаимному уничтожению.

И, во-вторых, ошибка модели должна быть мала, т. е. число фактически живущих должно мало отличаться от их значения, полученного по формуле Фёрстера.

Заблуждение Коротаева типично для гуманитария, никогда не имевшего дела с обработкой большого объема сильно «зашумленных» экспериментальных данных, когда при достаточно большом их количестве ошибка измерения может быть очень невелика.

Но это как раз именно такой случай. По мере удаления в прошлое данные по численности становятся все менее надежными, но общее их количество, использованное Фёрстером, настолько велико, что при совместной обработке оценки для показателя степенной функции и даты сингулярности оказываются очень точными. О чем это говорит? – О том, что ошибка модели мала. Но это как раз то, что и требовалось доказать. Следовательно, гиперболический рост населения Земли никакая не тенденция, как считает Коротаев, а надежно установленный закон.

* * *

Чрезвычайно высокая точность, с которой была определена гипербола мирового демографического роста в исследовании Фёрстера и его коллег, несомненно, связана с его устойчивостью. Причину такого парадоксального роста невозможно понять, не уяснив причины этой устойчивости. С.П. Капица считал, что не построенная до сих пор синергетическая модель гиперболического роста (модель второго типа по нашей классификации), асимптотикой которой является его феноменологическая теория, будет способна полностью объяснить эту устойчивость.

При этом в теории Капицы хотя и вводится константа характерного времени τ, однако она никак не связана ни с каким реально существующем циклическим историческим процессом. И устойчивость роста во все времена обеспечивается лишь его «устремленностью» на некоторую фиксированную гиперболу, выделенность которой, по мнению С.П. Капицы, может быть объяснена в будущем естественными причинами. В нашей модели устойчивость обеспечивается эквифинальностью циклического – по волнам Кондратьева – процесса роста и развития.

В обоих случаях демографический рост может отклоняться от гиперболы Фёрстера по причине войн, катастроф и эпидемий на весьма значительную величину, но всегда тем не менее возвращается на нее же. Именно поэтому в обоих случаях гипербола Фёрстера определяет закон гиперболического роста населения Земли. Закон, который может по-разному выражаться в разных теориях, претендующих на его объяснение, но это именно закон, а не тренд (тенденция), как считает Коротаев, который по самому своему определению ассоциируется с изменчивостью и неустойчивостью.

Демистификация по Коротаеву выглядит мистически

Переход от закона Фёрстера (2) к зависимости (1) рис. 1, по мнению Коротаева, существенно демистифицирует загадку гиперболического роста (выделено мной. – А.М.):

«Нельзя не отметить, что это существенно демистифицирует проблему объяснения гиперболической тенденции роста численности населения мира. Теперь для того, чтобы объяснить гиперболическую тенденцию роста численности населения мира, мы должны просто объяснить, почему на протяжении многих тысячелетий абсолютные темпы мирового демографического роста были в тенденции пропорциональны квадрату численности населения мира» [20] стр. 33.

Понятие «тенденция», которым Коротаев подменяет понятие «закон» в приведенной выдержке, в двух предложениях встречается трижды.

Рис. 1. Закон квадратичного роста скорости роста численности от численности (1), и гипербола Фёрстера – зависимость численности от времени (2).

Но объяснить дифференциальный закон, и в этом мы сейчас убедимся, ничуть не легче, чем закон Фёрстера. Действительно, при переходе от закона гиперболического роста, т. е. от гиперболической зависимости численности населения Земли от времени, к дифференциальному закону роста (квадратичной зависимости годового мирового естественного прироста от численности) необходимо решить две проблемы.

Первая проблема – это проблема каузальной интерпретации закона квадратичного роста (1), и заключается она в том, считать ли связь между численностью населения мира и ее годовым естественным приростом причинной, определяющей автокаталитический, самоускоряющийся процесс.

Как следует из приведенной выше выдержки, Коротаев такой проблемы вообще не видит: закон (1) подразумевается причинным, аналогичным закону экспоненциального роста. Т. е. считается, что он описывает положительную обратную связь второго (а не первого, как при экспоненциальном росте) порядка, что на самом деле совсем необязательно.

Вторая проблема демистификации по Коротаеву заключается в том, что приходится вводить неочевидный постулат, и постулат этот выглядит мистически. Действительно, все модели первого типа, простейшие из которых основаны на дифференциальном уравнении (1), не разделяют мировой естественный прирост численности – разницу между рождаемостью и смертностью за один год – на две составляющие: за счет рождаемости и за счет смертности (отрицательный ежегодный естественный «прирост»).

Эти статьи прироста имеют разную природу, и ниоткуда не следует, что их можно описывать одними и теми же уравнениями или составлять уравнения, содержащие только суммарный прирост. И проблема эта возникает в тот самый момент, когда от зависимости (2) мы переходим к ее дифференциальной форме (1).

Пока мы имеем дело с численностью как функцией времени – проблемы нет. А появляется она тогда, когда вводится в рассмотрение прирост численности или ее дифференциал. Т. е. для того, чтобы оперировать в уравнениях роста только с приростом численности, не интересуясь его составляющими, нужно вводить отдельный постулат. Коротаев этого даже не заметил!

Прирост численности за счет рождаемости зависит от множества факторов: социального, экономического, психологического, никак напрямую не связанных с факторами прироста за счет уменьшения смертности.

Каждая из составляющих прироста имеет свой список причин, который в обоих случаях, видимо, не имеет конца. Т. е. оба списка многочисленны, с невыясненным до конца составом и связями между их элементами. Очевидно, что каждая составляющая прироста должна присутствовать в законе роста численности независимо, отдельно от другой составляющей.

Мальтузианское допущение М. Кремера о том, что полная численность населения мира, а также ее прирост полностью определяются уровнем технологического развития (при этом можно не рассматривать отдельно каждую из статей прироста) — не в состоянии объяснить этот парадокс.

Дело в том, что новый уровень технологий во все времена, исключая последние десятилетия, давал прирост численности далеко не сразу: должно было смениться, по крайней мере, несколько поколений или пройти несколько периодов с длительностью равной характерному времени исторических изменений τ, равному примерно сорока годам.

Кроме того, время распространения технологий всегда было больше минимального времени проявления системности, значение которого не является константой, но во все исторические времена, исключая новейшее, было никак не меньше характерного времени исторических изменений.

Следовательно, для того чтобы объяснять закон (1), не разделяя прирост на две составляющие, нужно определять его на временах значительно больших сорока лет. Но гипербола Фёрстера (с точностью в 1 %) была получена при обработке демографических данных всего лишь за двадцать столетий, т. е. всего за 50 характерных времен, что явно противоречит допущению Кремера.

Кроме того, такой подход предполагает незначительный прирост численности за характерное время τ = 40 лет. Но этот прирост за время τ в последние столетия был соизмерим с общей численностью. В XX веке численность населения Земли за характерное время удвоилась, а рост все еще продолжался по закону той же самой гиперболы, которой следовал многие тысячи лет.

Поэтому уравнение (1), выражающее действующий причинный закон должно описывать прирост на временах меньших или даже значительно меньших характерного: Δt < τ. В таком случае разделение прироста на две составляющие: за счет рождаемости и за счет уменьшения смертности представляется совершенно необходимым.

Но записав простейшее уравнение (1) для суммарного прироста и проинтегрировав его, можно получить гиперболу Фёрстера. Почему такое возможно не менее загадочно, чем само явление гиперболического роста.

Возникает мистическое ощущение, что глобальная согласованность рождений и смертей по всей Ойкумене нацелена на то, чтобы общее число живущих в каждый (?) момент времени соответствовало некоторой «плановой» величине. Как мы покажем далее, такая согласованность может быть объяснена принципом эквифинальности роста и развития.

Демистификация по Коротаеву, т. е. переход от эмпирической зависимости (2) к причинному закону (1) (ПОС второго порядка), приводит к целому букету невыполнимых, невозможных следствий. Этот «букет мифов» мы сейчас и рассмотрим.

Миф о том, что только закон квадратичного роста

может обеспечить гиперболический рост

Чем же все-таки не устраивают модели первого типа, основанные на законе квадратичного роста (1) как на причинном законе, подумает придирчивый читатель? Что с того, что они редукционистские, если правильно описывают рост и к тому же наиболее просты по форме.

Рис. 1. Закон квадратичного роста скорости роста численности от численности (1), и гипербола Фёрстера: зависимость численности от времени (2).