
Полная версия:
Все аспекты деятельности испытательной лаборатории. Практическое пособие
Лаборатории, систематически выполняющие определение большого числа показателей, практически никогда не успевают все это делать, в лучшем, случае задним числом вычерчивая контрольные карты к очередной аккредитации или инспекционному контролю.
Проблема нашла свое решение с появлением компьютерных программ, позволяющих полностью или частично автоматизировать ВЛК, проводя расчеты с помощью компьютера и отказавшись от ведения контрольных карт в бумажной форме.
4.4. Контроль стабильности результатов испытаний
Выделяют следующие формы контроля стабильности результатов испытаний:
1. Контроль за стабильностью результатов испытаний в конкретной лаборатории с применением контрольных карт путем поддержания на заданном уровне:
– характеристик погрешности результатов испытаний;
– показателей внутрилабораторной прецизионности, в том числе значений повторяемости результатов параллельных испытаний;
2. Систематическая проверка подконтрольности процедур осуществления измерений (испытаний, анализа);
3. Выборочный статистический контроль показателей внутрилабораторной прецизионности и погрешности результатов испытаний, выполненных в течение заданного промежутка времени.
Анализ информации, полученной при контроле стабильности результатов, позволяет осуществить оценку внутрилабораторной прецизионности, погрешности результатов испытаний, проводить их сопоставление с установленными значениями, а также реализовывать контроль систематической погрешности в данной лаборатории.
С целью обеспечения качества при реализации внутрилабораторного контроля ежегодно составляется график построения и проверки градуировочных характеристик, а также предусматривается проведение контроля методом добавок, разведения, использования образца для контроля, ведется контроль погрешности на основе применения контрольных проб с использованием контрольных карт.
Контроль за стабильностью результатов испытаний основан на оценке величины систематической и случайной погрешности.
Систематическая погрешность всегда сдвигает результаты в одну и ту же сторону, случайная же погрешность меняется по значению и зависит от многих случайных изменений (например, внешних условий). Систематическая погрешность – это составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Систематическая погрешность определяется близостью среднего результата повторных измерений контрольного материала к аттестованному значению измеряемой величины (далее – АЗ).
Случайная погрешность – это составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Отследить случайную ошибку гораздо сложнее, чем систематическую, также, как и выявить причину ее возникновения. Случайные погрешности являются неустранимыми, и только тщательно налаженная стандартизация всех этапов анализа, строгое соблюдение условий исследования и учет многочисленных факторов, влияющих на анализ, позволяют свести случайную погрешность измерения к минимуму. К случайной погрешности, как правило, относится и промах (грубая погрешность измерений), характеризующийся тем, что погрешность результата отдельного измерения, входящего в ряд измерений, для данных условий резко отличается от остальных результатов этого ряда.
Грубые ошибки – это ошибки одиночного значения, когда результаты исследований выходят за пределы области определяемого компонента. Эти ошибки могут быть субъективными, которые зависят от квалификации специалиста, недостаточной тщательности его работы.
Возникают ошибки обычно из-за недосмотра: ошибка при регистрации результата, неправильное дозирование пробы, перепутан реактив, неподходящий фильтр при фотометрии, ошибка в разведении, подсчете, небрежность в проведении метода исследования и т. д.
Грубые ошибки могут быть и объективными, зависящими от чистоты лабораторной посуды, реактивов, состояния приборов и др.
Грубая погрешность существенно превышает ожидаемую погрешность и, как правило, видна невооруженным глазом. Такие результаты отбрасываются, и производится повторный анализ пробы.
Сочетание случайных и систематических погрешностей показано на рис. 4.3.
Воспроизводимость и правильность являются основными показателями качества результата лабораторного анализа, потому что они характеризуют полную ожидаемую ошибку результата лабораторного измерения, другими словами, показывают, насколько измеряемое содержание в пробе исследуемого параметра будет отличаться от его «истинного» значения.
Воспроизводимость – качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях (т.е. степень совпадения результатов повторных измерений одной и той же пробы). Воспроизводимость измерений характеризует наличие случайных погрешностей.
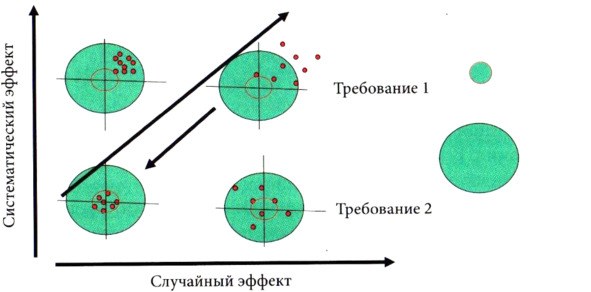
Рисунок 4.3 – Сочетание случайных и систематических погрешностей
Правильность – качество измерений, отражающее близость к нулю систематических погрешностей в результатах (рис. 4.4). Правильность измерений характеризует наличие систематических погрешностей.
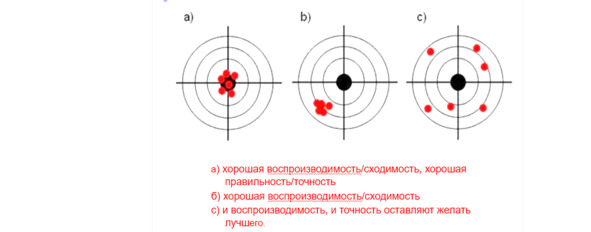
Рисунок 4.4 – Иллюстрация правильности и воспроизводимости результатов анализа
В ГОСТ Р ИСО 5725—2002 вводится общий термин «прецизионность» для всех видов случайных погрешностей. Прецизионность – степень близости или степень разброса результатов для серии измерений, выполненных по данной методике на различных пробах одного и того же однородного образца. Прецизионность может рассматриваться на трех уровнях: сходимость, внутрилабораторная прецизионность и воспроизводимость.
Воспроизводимость результатов измерений – отсутствие существенных различий между результатами измерений, выполняемых в одинаковых условиях. Контроль сходимости и воспроизводимости результатов исследований может осуществляться с помощью контрольного материала с неисследованным содержанием.
Термины «повторяемость» и «сходимость» становятся синонимами и относятся к измерениям, выполняемым в течение краткого промежутка времени, одним исполнителем, на одном и тем же оборудовании, с использованием одних и тех же реактивов и т.д., т. е. «в условиях повторяемости».
Мерой повторяемости (сходимости) является дисперсия повторяемости s2r. Другими словами, это минимально возможная для методики измерений систематическая погрешность. Дисперсия дает характеристику разброса данных вокруг центра.
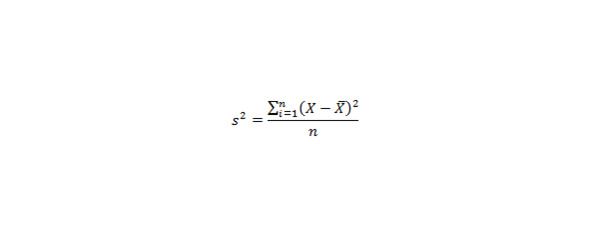
где s2 – выборочная дисперсия; X – отдельные значения; X̅ – среднее арифметическое по выборке.
Дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средним арифметическим значением отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и, чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, мы просто рассчитываем среднее арифметическое значение. Однако в чистом виде, как, например, средняя арифметическая, дисперсия не используется. Это скорее вспомогательный и промежуточный показатель, который необходим для других видов статистического анализа. У нее нет даже единицы измерения. Для того, чтобы использовать дисперсию, из нее извлекают квадратный корень, получается среднеквадратичное отклонение (далее – СКО).
СКО вычисляется по формуле:
S = (Σ (xi – X̅) 2 /n (n – 1) 1/2
где xi – результат i-го измерения из n выполненных;
X̅ – среднее арифметическое значение.
Среднее арифметическое значение определяют как сумму всех результатов измерений делённую на количество измерений.
Математически, случайная погрешность может быть выражена не только величиной СКО, но и коэффициентом вариации (далее – CV). СКО дает абсолютную оценку меры разброса, поэтому, чтобы понять, насколько разброс велик относительно самих значений, т.е. независимо от их масштаба, требуется относительный показатель – коэффициент вариации.
Коэффициент вариации — это величина, равная отношению стандартного (среднеквадратичного) отклонения случайной величины к ее математическому ожиданию (Хср.). Он применяется для сравнения вариативности одного и того же признака в нескольких совокупностях с различным средним арифметическим. Коэффициент вариации—это стандартное отклонение, выраженное в процентах от среднего значения.
CV = S 100% / X̅
Этот показатель вариации хорош тем, что и меру рассеяния учитывает, и единиц измерения не имеет, то есть совершенно не связан с масштабом анализируемых данных. Исходя из этого факта, коэффициенты вариации можно сравнивать между собой и тем самым сопоставлять относительную меру рассеяния данных, независимо от их масштаба.
В теории измерений принято, что:
– если коэффициент вариации меньше 10%, то степень рассеивания данных считается незначительной;
– если от 10% до 20% — степень рассеивания данных считается средней;
– больше 20% и меньше или равно 33% — степень рассеивания данных считается значительной.
Что это означает?
Рассмотрим пример выборки с коэффициентом вариации 45% (рис. 4.5).
На графике видно, что диапазон разброса до плюс/минус 80, совокупность результатов анализа неоднородна.
Рассмотрим пример выборки с коэффициентом вариации 24% (рис. 4.6).
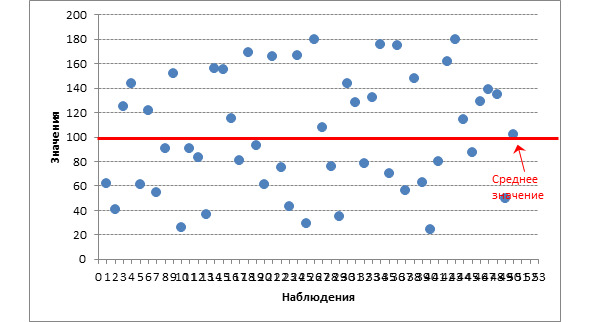
Рисунок 4.5 —Пример выборки с коэффициентом вариации 45%
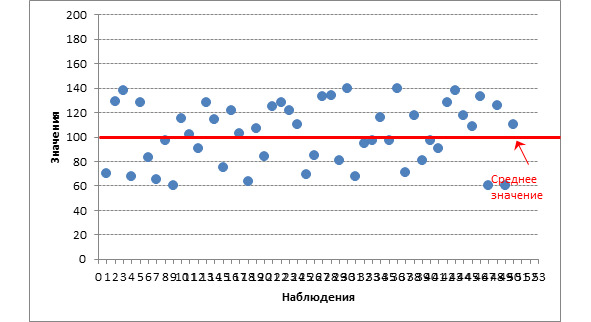
Рисунок 4.6 – Пример выборки с коэффициентом вариации 24%
При сравнении графиков видны отличия однородных данных от неоднородных. На втором графике – данные однородны со значением коэффициента вариации 24%, на первом – неоднородны со значением вариации 45%. Чем более однородны данные, тем ближе они находятся к среднему значению. Чем менее однородны, тем больше рассеяны и находятся дальше друг от друга и от своей средней.
Если показатель вариации составляет примерно 30% и меньше, то статистическая совокупность считается однородной. Это означает, что большинство показателей находится недалеко от среднего арифметического значения, и найденное значение хорошо характеризует центральную тенденцию совокупности. Если показатель вариации составляет существенно больше 30%, то выборка неоднородна, то есть, значительное количество показателей находится далеко от, и среднее арифметическое значение плохо характеризует правильный результат.
Запись результата измерения должна сопровождаться указанием его надежности P. Под надежностью или доверительной вероятностью понимают вероятность того, что истинное значение измеряемой величины заключено в интервале, указанном записью. Сам этот интервал называется доверительным интервалом.
Вероятность α того, что истинное значение случайной величины xi находится внутри некоторого интервала от <x> —∆x до <x> + ∆x, называется доверительной вероятностью или коэффициентом надёжности, а сам интервал – доверительным интервалом. Чем больше доверительный интервал, т.е. чем больше задаваемая погрешность результата измерений, тем с большей надёжностью искомая величина попадёт в этот интервал.
Например, измеряя длину некоторого отрезка, окончательный результат записан в виде L = (8.34 ± 0.02) мм, (P = 0.95)
Это означает, что 95 шансов из 100 шансов за то, что истинное значение длины отрезка заключается в интервале от 8.32 до 8.36 мм. Например, ГОСТы на методы испытаний требуют, чтобы запись результата анализа была сделана как результат среднеарифметического показателя двух результатов измерений, расхождение между которыми не должно превышать 0,5% при Р=0,95%.
Доверительной вероятностью (надежностью) результата серии наблюдений называется вероятность α, с которой доверительный интервал включает истинное значение измеряемой величины (рис. 4.7).
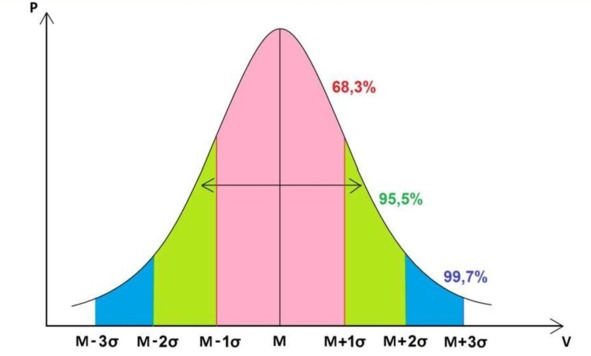
Рисунок 4.7 – Доверительный интервал
Значение α = 0,955, например, означает, что 95,5% проведенных измерений xi будут иметь отклонения от среднего <x> меньшие, чем 2Sx, и лишь для пяти процентов (т.е. каждое двадцатое) отклонения выйдут за этот интервал. Таким образом, задавая вероятность (надежность) измерений, мы тем самым устанавливаем интервал допустимых абсолютных ошибок.
Повторяемость (сходимость) результатов испытаний – это характеристика результатов испытаний, определяемая близостью результатов испытаний одного и того же объекта по одной и той же методике в соответствии с требованиями одного и того же нормативного документа в одной и той же лаборатории одним и тем же оператором с использованием одного и того же экземпляра оборудования в течение короткого промежутка времени.
Норматив (предел) повторяемости (сходимости) – предельно допускаемое абсолютное расхождение между двумя результатами испытаний, полученными в условиях повторяемости (сходимости), для доверительной вероятности 0,95.
Воспроизводимость результатов испытаний определяется как характеристика результатов испытаний, определяемая близостью результатов испытаний одного и того же объекта по единым методикам в соответствии с требованиями одного и того же нормативного документа с применением различных экземпляров оборудования разными операторами в разное время. Такие условия обеспечиваются при проведении испытаний в разных лабораториях (межлабораторный контроль).
Термин «воспроизводимость» связан с межлабораторным разбросом результатов измерений. Таким образом, в применении к внутрилабораторному контролю термин «воспроизводимость» вообще использоваться не должен: для отдельно взятой лаборатории, так как соответствующий эффект уже не является случайным; он вырождается в систематическую погрешность этой лаборатории. Однако, при обычной в лабораторной практике ситуации, когда разные группы проб исследуются на одном и том же оборудовании, одним и тем же лаборантом, но в разное время и с использованием разной калибровки, может возникнуть случайная погрешность, которая выявляется путем оценки вопроизводимости. При записи результатов рекомендуется указывать, какие именно факторы изменяются. Всего рассматриваются четыре фактора (время T, калибровка C, оператор O, оборудование E).
Норматив (предел) воспроизводимости – предельно допускаемое абсолютное расхождение между двумя результатами испытаний, полученными в условиях воспроизводимости, для доверительной вероятности 0,95.
При малом числе измерений заданному значению α соответствует больший доверительный интервал.
При расчете случайной погрешности задаются надежностью измерений, которую, в зависимости от целей измерений и требований к ним, принимают равной 0,9; 0,95; 0,96; 0,98; 0,99; 0,997; 0,999.
Чем больше доверительная вероятность, тем надежнее оценка интервала и, вместе с тем, шире его границы.
Случайную составляющую погрешности принято выражать как полуширину доверительного интервала. Размер доверительного интервала обычно задают в виде кратного S
Δx=tα (N) S
где tα (N) – безразмерный коэффициент доверия (коэффициент Стьюдента).
Множители, определяющие величину интервала в долях Sa в зависимости от α и N, называются коэффициентами Стьюдента. Они обозначаются через tα (N) и находятся из таблицы.
Что же это такое? Применительно к нормальному закону распределения значения коэффициентов охвата были впервые рассчитаны английским математиком У. Госсетом, подписывавшим свои труды псевдонимом Стьюдент, и потому называются коэффициентами Стьюдента. Коэффициенты Стьюдента имеют специальное обозначение t. Таким образом, в предположении подчинения случайной величины x нормальному закону распределения формула для расчета ее доверительного интервала принимает вид x ± t (P, f) s (x). Коэффициенты Стьюдента зависят от двух параметров: доверительной вероятности P и числа степеней свободы f, соответствующего стандартному отклонению s (x).
Причина зависимости t от P очевидна: чем выше доверительная вероятность, тем шире должен быть доверительный интервал с тем, чтобы можно было гарантировать попадание в него значения величины x. Поэтому с ростом P значения t возрастают. Зависимость t от f объясняется следующим образом. Поскольку s (x) – величина случайная, то в силу случайных причин ее значение может оказаться заниженным. В этом случае и доверительный интервал окажется более узким, и попадание в него значения величины x уже не может быть гарантировано с заданной доверительной вероятностью. Чтобы «подстраховаться» от подобных неприятностей, следует расширить доверительный интервал, увеличить значение t, причем тем больше, чем менее надежно известно значение s, т.е. чем меньше число его степеней свободы. Поэтому с уменьшением f величины t возрастают. Коэффициенты Стьюдента для различных значений P и f приведены в табл. 4.1.
Таблица 4.1
Коэффициенты Стьюдента
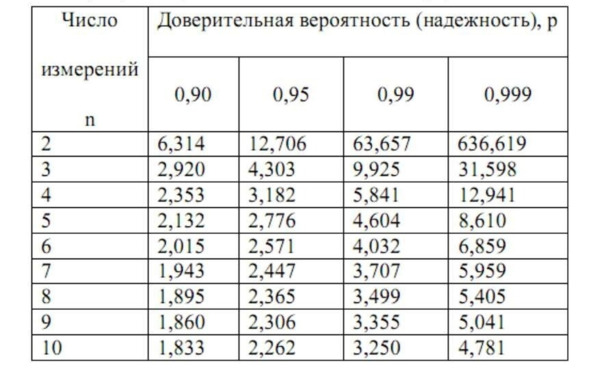
При расчете доверительного интервала встает вопрос о выборе доверительной вероятности P. При слишком малых значениях P выводы становятся недостаточно надежными. Слишком большие (близкие к 1) значения брать тоже нецелесообразно, так как в этом случае доверительные интервалы оказываются слишком широкими, малоинформативными. Для большинства химико-аналитических задач оптимальным значением P является 0,95.
Пример 1. Микрометром N раз измерялся диаметр d стержня (систематическая ошибка измерения равна 0,005мм). Результаты измерений заносим во вторую графу таблицы 4.2, находим среднее арифметическое значение:
В третью графу таблицы записываем разности между каждым измерением и средней арифметической величиной, а в четвертой графе возводим эти величины в квадрат.
Результаты измерения
Номер измерения 1
Длина стержня d, мм 4.02
Разность между средним и i-тым значением +0.01
Квадрат разности 0.0001
Номер измерения 2
Длина стержня d, мм 3.98
Разность между средним и i-тым значением – 0.03
Квадрат разности 0.0009
Номер измерения 3
Длина стержня d, мм 3.97
Разность между средним и i-тым значением – 0.04
Квадрат разности 0.0016
Номер измерения 4
Длина стержня d, мм 4.01
Разность между средним и i-тым значением +0.00
Квадрат разности 0.0000
Номер измерения 5
Длина стержня d, мм 4.05
Разность между средним и i-тым значением +0.04
Квадрат разности 0.0016
Номер измерения 6
Длина стержня d, мм 4.03
Разность между средним и i-тым значением +0.02
Квадрат разности 0.0004
Σ измерений длин стержня =24.06
Σ квадратов разности = 0.0046
Далее определяем среднее квадратичное отклонение, с учётом выборки с количеством измерений менее 10 в знаменателе применяем n (n-1):
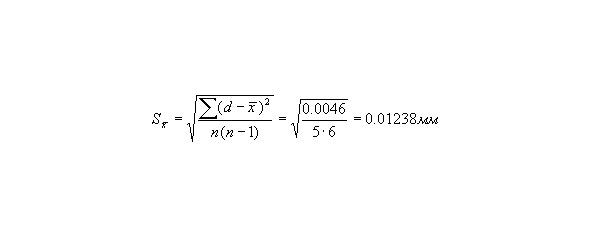
Коэффициент вариации: CV=0,01238*100/4,01=0,3 (степень рассеивания незначительная).
Задавшись надежностью P=0,95, по таблице коэффициентов Стьюдента для шести измерений найдем t = 2,571. Абсолютная ошибка найдется по формуле:
Δх = 0.01238*2.571 = 0.04мм.
Сравним случайную и систематическую ошибки: следовательно, δ = 0,005 мм можно отбросить. Окончательный результат запишем в виде d = (4.01 ± 0.04) мм при Р = 0.95.
Относительная ошибка составляет 1%.
Контроль стабильности результатов анализа может предусматривать следующие формы:
1) контроль стабильности результатов анализа с использованием контрольных карт;
2) оценка характеристик внутрилабораторной прецизионности, систематической погрешности лаборатории, погрешности результатов анализа и их сопоставление с установленными значениями.
Достоверность выводов о качестве результатов анализа зависит от реализуемой формы контроля стабильности результатов анализа, используемого числа контрольных процедур, частоты их проведения.
Требования к проведению контрольных измерений (определений) аналогичны требованиям к проведению анализа рабочих проб, установленным в нормативной документации, регламентирующей методику анализа.
Роль средств контроля могут выполнять:
– образцы для контроля: стандартные образцы по ГОСТ 8.315 или аттестованные смеси;
– рабочие пробы с известной добавкой определяемого компонента;
– рабочие пробы, разбавленные в определенном отношении;
– рабочие пробы, разбавленные в определенном отношении с известной добавкой определяемого компонента;
– рабочие пробы стабильного состава;
– другие методики анализа с установленными показателями качества (контрольные методики).
Контроль стабильности результатов анализа с использованием контрольных карт является визуальным средством обнаружения динамики изменений показателей качества результатов анализа, последующего установления причин этого изменения и оперативного управления качеством анализа на основе установленных при работе с контрольными картами правил рассмотрения возникающих ситуаций.
Информация о статистических оценках показателей качества результатов анализа, получаемая при контроле стабильности результатов анализа с использованием контрольных карт, позволяет провести достоверную оценку систематической погрешности лаборатории, СКО, внутрилабораторной прецизионности и в целом погрешности результатов анализа.
Контроль стабильности результатов анализа с использованием контрольных карт представляет собой графический способ контроля показателей качества результатов анализа. Для организации контроля стабильности результатов анализа с использованием контрольных карт определяют:
– необходимое число контрольных процедур для достоверной оценки каждого из контролируемых показателей качества результатов анализа;
– временной диапазон для получения необходимого числа контрольных процедур (далее – временной диапазон), устанавливаемый с учетом: длительности процедуры выполнения анализа, стоимости анализа, взаимосвязи числа контрольных процедур с числом рабочих проб, анализируемых за определенный период времени.
Контрольные карты применяются для контроля стабильности процесса измерений и выявления ситуаций выхода этого процесса из статистически контролируемого состояния. Они представляют собой графики, на которых по горизонтальной оси откладывают порядковый номер исследования, а по вертикальной – результаты измерения какого-либо показателя качества исследований. На эти карты наносятся в виде горизонтальных прямых «пределы», и выход результата за эти пределы свидетельствует о нестабильности процесса измерений (рис. 4.8).
Границы ±3S указывают, что около 99,7% значений попадут в эти пределы при условии, что процесс измерений находится в статистически управляемом состоянии, т.е., есть риск, равный 0,3%, что нанесенная точка окажется вне контрольных границ. Вероятность того, что нарушение границ на самом деле случайное событие, а не реальный сигнал, считается столь малым, что при появлении точки вне границ следует предпринять определенные действия. Т.к. действия предпринимаются именно в этой точке, то границы ±3S называют «Предел действия». «Контрольный признак» – это событие, свидетельствующее о выходе процесса из статистически контролируемого состояния с доверительной вероятностью, превышающей ~0,99, и требующее остановки исследований и коррекции процесса измерений «предел действия» Строго говоря, после коррекции необходимо повторно исследовать рутинные пробы.

