Население Земли как растущая иерархическая сеть

Для обоснования этого абсурдного вывода Подлазов использует данные М. Кремера по динамике роста населения Китая, Индии и Европы. Рост каждого из этих регионов, по его мнению, по факту был примерно гиперболическим, поскольку доля населения этих стран по отношению ко всему населению Земли всегда оставалась приблизительно постоянной. В доказательство этого утверждения он приводит графики роста населения Китая, Индии и Европы в долях относительно населения мира за период от 200 года до н. э. до 2000 года:

«Как можно видеть из рис. 5, относительное количество людей, проживающих в крупнейших регионах мира, остается примерно постоянным на протяжении значительного времени. Поэтому динамика их населения должна быть, по крайней мере, качественно такой же, как и динамика всего человечества» [52].

Однако, даже по данным Кремера тридцатилетней давности, которые использует Подлазов, размах колебаний численности для каждого из этих регионов составляет величину, большую десяти процентов. Фактическое же ее значение для Китая, Индии и Европы за выделенный период могло отклоняться от осредненных данных Кремера на десятки процентов. Поэтому его утверждение о том, что динамика их роста была «качественно такой же, как и динамика всего человечества», т. е. примерно гиперболической, является ошибочным.

Сравнивая свою модель с моделями Капицы и Коротаева, Подлазов подсчитывает для них зависимость темпа прироста населения от численности. Для построения реальной зависимости темпа от численности он использует временной ряд, взятый все из той же работы М. Кремера. При этом численность меняется в пределах от нуля до семи миллиардов, а темп прироста от нуля до двух процентов, т. е. рассматривается рост населения Земли во всем диапазоне исторического времени.

При построении графиков Подлазов использует как авторские параметры моделей Капицы и Коротаева, так и параметры, обеспечивающие наилучшее приближение графика темпов. Вывод его однозначен:

«Ни одна из классических моделей не может приблизить реальные графики прироста и его темпов, тогда как соответствие динамики авторской модели демографическим данным следует признать удовлетворительным» [52].

При этом Подлазов «забывает» отметить, что данные по «реальным» темпам прироста численности по годам от начала н. э. до XX века, которые он использует, имеют не меньшую, если не большую погрешность, чем данные по численности, т. е. она составляет по мере ухода в прошлое многие десятки процентов. О каком тогда удовлетворительном соответствии его модели может идти речь?

Хотелось бы также заметить следующее: называя модели Капицы и Коротаева классическими, Подлазов, очевидно, считает их равноправными гипотезами, т. е. не видит между ними никакой в эвристическом смысле разницы. Между тем модель Капицы с ее константами К и τ, циклами эволюции и истории, сжатием исторического времени, т. е. с теми ее несомненными достижениями, которые даже не упоминаются в псевдонаучной теории Коротаева, не может быть поставлена с последней в один ряд. (То же самое, кстати, можно сказать и о модели самого Подлазова.)

Акцентируя внимание на жизнесберегающих технологиях, продлевающих жизнь и увеличивающих численность народонаселения, Подлазов никак не отмечает жизнеуничтожающие технологии, укорачивающие человеческую жизнь, такие, как то же «воинское искусство», определяемое им как чисто жизнесберегающее, способы производства всех видов наркотических веществ, табачных изделий, алкоголя… Сюда же можно включить жизнеуничтожающие факторы и привычки, которые нельзя назвать технологиями. В наше время это, прежде всего, вирусные и бактериальные инфекции, наследственные заболевания всех видов, неправильное питание, малоподвижный образ жизни, халатное отношение к своему здоровью и т. д. и т. п. А ведь такой подход к технологиям и факторам, влияющим на продолжительность жизни, по крайней мере в наше время, является гораздо более адекватным.

Очевидным недостатком, если не сказать пороком, модели Подлазова является то, что решения предложенного им уравнения, описывающие гиперболический рост человечества и демографический переход, не обладают устойчивостью. (Устойчивостью обладает лишь стационарный режим за переходом, когда скорость роста меняет свой знак при достижении численностью предельного значения.) Малейшие возмущения быстро уводят рост с текущей гиперболы и сдвигают время перехода, что, кстати, автором никак не отмечено. А ведь устойчивость гиперболического роста является совершенно необходимым его условием, т. к. после любого случайного взлета или спада численности рост всегда должен возвращаться на изначальную гиперболу.

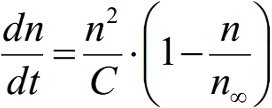
Рис. 1. Уравнение Подлазова, не имеющее устойчивых решений и потому неспособное объяснить феномен гиперболического роста населения Земли. Может рассматриваться как регрессионная зависимость, т. е. как формула, описывающая связь между численностью и скоростью ее роста и не претендующая на описание причинно-следственных отношений между ними [52].

Возможна даже более широкая постановка вопроса. Можем ли мы, собственно, быть уверены в том, что столь сложный, многомерный процесс, зависящий от всего своего прошлого, каким является рост населения Земли (и рост жизнесберегающих технологий), должен описываться на языке аппарата дифференциальных уравнений? Ведь всякое дифференциальное уравнение есть, по сути, рекуррентное соотношение, позволяющее полностью определять текущее состояние процесса по его состоянию в бесконечно близкий момент времени в прошлом. Такой подход к проблеме роста технологий и населения Земли, по нашему мнению, может оказаться неверным в принципе, заводящим любое исследование в тупик.

Точность (в один процент!), с которой определились показатель степенной функции, описывающей гиперболический рост, и дата сингулярности в классическом исследовании Фёрстера и его коллег, не может быть объяснена ростом жизнесберегающих технологий, который во все времена представлял собой стохастический, зависящий от всего своего прошлого, нелинейный процесс. Это на интуитивном уровне понятно любому мало-мальски мыслящему человеку.

Кроме того, технологическая модель Подлазова не содержит никакого указания на цикличность исторического развития, связанную с растущей численностью, отмеченную многими исследователями. Не найдете вы в ней также никакого объяснения явлению сжатия исторического времени в ходе такого циклического развития, о котором много и подробно писал С.П. Капица.

Заметим также, что модели пространственно-распределенных систем, которые традиционно изучает синергетика и каковой является растущее население Земли, включают как временно́й, так и пространственный анализ эволюции таких систем. Странно, что А.В. Подлазов, который является апологетом синергетики, не только не делает никаких попыток обобщить свою модель роста сосредоточенной популяции до модели, учитывающей пространственное распределение, но нигде даже не упоминает о такой необходимости.

* * *

Заключение. Можно ли считать предельно упрощенную, однопричинную модель Подлазова гомоморфной столь сложному многофакторному процессу, каким является рост населения Земли? – Вряд ли. Есть даже сомнения в научности предложенной теории, ведь не существует никакого способа ее проверить и, кроме того, она ничего не предсказывает. В то же время нельзя не отметить логическую строгость и математическую точность построений Подлазова.

Выводы, к которым он приходит (за исключением технологического императива), на наш взгляд, совершенно верны. Это касается предела роста, который в модели Подлазова обусловлен неспособностью жизнесберегающих технологий увеличивать сверх биологического максимума продолжительность человеческой жизни, и конца истории в привычном ее понимании:

«Рост народонаселения обусловлен расширением технологической ниши человечества вследствие развития им жизнесберегающих технологий. Их мерой служит достигнутое за счет их действия сокращение коэффициента смертности. Его приближение к естественным пределам ограничивает возможности дальнейшего увеличения людской численности, а тем самым и того способа развития, который человек практиковал с момента своего выхода из животного мира. История, какой мы ее знаем, близится к концу, что грозит стать самым жестоким кризисом, с которым сталкивалась цивилизация» [52].

Рост населения Земли в процессе глобального демографического перехода в XXI веке происходил, происходит и будет происходить не по причине роста рождаемости, а за счет увеличения продолжительности жизни. (Представление о высокой рождаемости в азиатском регионе планеты в наше время является мифом.) Усредненная по всем странам и народам рождаемость (Р) падает в процессе перехода, падает и смертность (С) по причине роста жизнесберегающих технологий. Годовой мировой естественный прирост (Р – С) в конце перехода устремится к нулю, когда предельное значение второго члена этой разности (С) сравняется с падающей рождаемостью (Р).

Предельная численность населения мира ограничена средней продолжительностью человеческой жизни в максимально благоприятных условиях. В качестве иллюстрации этого положения приведем график вероятности «оставаться живым» от возраста в современной Германии.

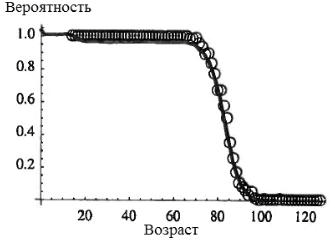
Рис. 2. Зависимость вероятности «быть живым» от возраста в современной благополучной Германии [54].

В возрастном интервале от 70 до 80 лет у средне-статистического человека начинается генетически запрограммированное разрушение основных органов и систем организма. Процесс старения нельзя остановить, биологическая смерть абсолютно неизбежна, ее можно лишь отсрочить. Именно поэтому численность населения Земли после глобального демографического перехода за счет жизнесберегающих технологий расти больше не будет.

Каков же итог? Технологический императив Подлазова так же несостоятелен, как демографический императив Капицы, новационный императив Коротаева, энергетический императив Веллера, информационный императив Долгоносова. Обилие конкурирующих однопричинных моделей говорит об ущербности каждой из них, взятой по отдельности, для описания столь сложной системы, какой является растущее человечество, и необходимости построения многопричинной модели эволюции, роста и развития.

Миф о том, что закон квадратичного роста как причинный закон роста численности популяции встречается в природе

По мнению С.П. Капицы, «…секрет гиперболического, взрывного развития состоит в том, что скорость роста пропорциональна квадрату численности населения мира» [1]. На самом же деле главный секрет здесь в том, что гиперболический рост численности популяций любых организмов, а также множества частиц в физических и химических реакциях под действием общесистемного причинного закона (1) – НИКОГДА не встречается в природе.

В дальнейшем, если это не будет оговорено специально, закон (1) будем считать причинным законом в том смысле, в каком он был определен нами ранее. Таковым же, несомненно, считал этот закон и С.П. Капица, интерпретируя его как закон «коллективного взаимодействия».

Рис. 1. Закон квадратичного роста. Скорость роста численности населения мира пропорциональна квадрату численности.

В своих многочисленных выступлениях и публикациях С.П. Капица приводит графики линейного, экспоненциального и гиперболического роста в качестве иллюстрации возможных сценариев роста населения Земли [21].

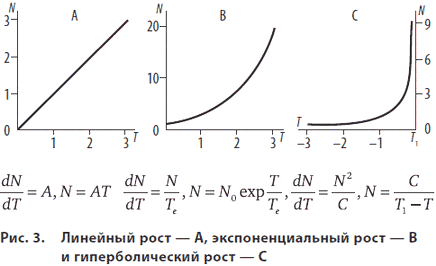
Рис. 2. Возможные сценарии роста численности человечества по С.П. Капице. Скорость роста постоянна или пропорциональна первой и второй степени численности.

Законы роста как причинные законы здесь схожи, но рост в каждом из трех случаев имеет свои особенности. Так, линейный и гиперболический рост как степенные законы самоподобны, чего не скажешь об экспоненциальном росте. Кроме того, считая закон (1) причинным законом, С.П. Капица акцентирует внимание читателя на том, что численность популяции устремляется к бесконечности за конечный промежуток времени.

Что в случае роста численности человечества приводит, по его мнению, к режиму с обострением, выход из которого С.П. Капица, используя терминологию термодинамики, называет фазовым переходом. В этом и состоит, по мнению С.П. Капицы, главное отличие моделей гиперболического и экспоненциального роста.

После прочтения этого текста и просмотра иллюстраций у читателя возникает впечатление, что закон квадратичного роста как причинный закон явление обычное и встречается в природе достаточно часто. С.П. Капица в своей книге [21] приводит тому ряд примеров. На самом же деле между законами экспоненциального и гиперболического роста численности популяции (законами В и С) лежит непреодолимая пропасть:

Если численность популяции растет по экспоненциальному закону, то для любого момента роста, независимо от его расположения на оси времени, существует такой отрезок времени, неизменный на всей шкале этого роста, в течение которого ее численность удваивается; т. е. рост здесь происходит по закону геометрической прогрессии на последовательности интервалов времени равных по своей длительности. Поэтому закон экспоненциального роста, в отличие от закона степенного роста, имеет встроенный масштаб времени: неизменное, не зависящее ни от внешних, ни от внутренних условий (прежде всего, от численности) время удвоения ее численности.

Для гиперболического роста, подобного росту населения Земли, также можно подобрать такую последовательность интервалов времени. Отличие здесь в том, что длительность этих интервалов удвоения численности не остается постоянной, как в случае экспоненциального роста. А сокращается по закону той же самой прогрессии, по которому растет численность по истечении каждого такого интервала (т. е. удвоение численности достигается на каждом последующем интервале за время в два раза меньшее, чем на предыдущем).

И сходится эта последовательность к некоторой точке на оси времени – точке сингулярности гиперболы роста. Поскольку численность популяции при этом за конечное время неограниченно возрастает, потенциальная бесконечность идеального экспоненциального роста трансформируется здесь в актуальную бесконечность идеального гиперболического роста. Потенциальная возможность неограниченного возрастания численности идеального экспоненциального роста качественным образом отличается от актуальной бесконечности, которой достигает численность в точке сингулярности идеального гиперболического роста.

При первом чтении приводимые далее примеры можно пропустить.

* * *

Для более ясного представления о том, что такое причинный закон рассмотрим несколько примеров экспоненциального роста:

1. Размножение микроорганизмов в чашке Петри с питательной средой.

2. Рост числа разделившихся ядер в цепной ядерной реакции.

3. Экспоненциальный рост популяции животных с полигамной ориентацией.

4. Экспоненциальный рост популяции моногамных животных.

Во всех случаях прирост численности «частиц» пропорционален их общему числу N, но причинно-следственная цепь событий, создающая в каждой системе этот прирост ΔN за малый промежуток времени Δt, в каждом из четырех приведенных примеров будет своя.

Так, каждый из разделившихся микроорганизмов ничем не отличается от материнского и продолжает участвовать в процессе размножения точно в таком же качестве. Чего не скажешь про осколки разделившегося ядра в цепной ядерной реакции, которые никакого участия в дальнейшем размножении распавшихся ядер уже не принимают.

В случае полигамии любая пара противоположного пола может дать потомство, в то время как в популяции моногамных животных пары устойчивы и не имеют других партнеров.

Несмотря на различную природу роста численности таких популяций, сама схема роста во всех случаях одинакова: … → N → события определяющие прирост → прирост ΔN за Δt → N + ΔN →… Здесь прирост ΔN за малый промежуток времени Δt складывается с текущей численностью N, образуя при этом элементарное звено причинно-следственной цепи.

События, включенные в это звено, в каждом случае свои, но объединяет их одинаковый, экспоненциальный механизм роста. Закон экспоненциального роста для всех приведенных примеров может считаться причинным законом, т. к. существуют эндогенные события-причины, т. е. события, вызванные внутренними системными факторами, приводящими к приросту ΔN.

Эти события зависят только от численности «частиц» N: ΔN ~ N и не выходят за пределы промежутка времени t – t + Δt, где Δt – это достаточно малый шаг итерации; достаточно малый в том смысле, что при работе рекуррентного алгоритма в пределе возможен переход к уравнению причинного закона dN/dt = αN.

При этом события-причины, составляющие элементарное звено причинно-следственной цепи, сами образуют причинно-следственную цепь элементарных событий с простой, непосредственной преддетерминацией, каждое предшествующее событие в которой является причиной последующего.

Вернемся к рассмотренному ранее примеру об экспоненциальном и гиперболическом росте колонии микроорганизмов, идущем в соответствии с причинными законами (1) и (2).

Рис. 3. Экспоненциальный и гиперболический рост численности популяции.

Считаем, что показатель смертности в обоих случаях равен нулю. Рассмотрим сначала экспоненциальный рост по закону (2). В простейшем случае, когда каждый новорожденный организм спустя некоторое время τ = 1/α = const делится на два идентичных, шаг итераций должен быть выбран гораздо меньше этого τ – времени, характеризующего рост: Δt << τ.

Т. к. показатель смертности равен нулю, то τ = 1/α – это время, необходимому микроорганизму, чтобы создать свою копию. Шаг итераций Δt не может быть соизмерим и тем более быть большим τ, т. к. за это характерное время численность N возрастает в 2.7 раза, а приращение ΔN при малом Δt также должно быть мало.

Других ограничений на Δt – нет (считаем, что объем питательной смеси неограничен, а фаза – стадия развития микробов в колонии распределена равномерно на интервале τ) и при достаточно малом шаге Δt можно перейти к простейшему дифференциальному уравнению с экспоненциальным решением.

Усложним процесс следующим образом: пусть микроорганизм в процессе деления за время τ создает сразу две, три или большее число собственных копий. Или даже будем считать, что число копий в результате каждой такой операции деления, происходящей с периодом τ, есть величина случайная, принимающая значения от нуля до бесконечности и распределенная в соответствии с единым для всех организмов законом. (Тогда можно ввести средний коэффициент прироста α = k/τ.)

И во всех этих случаях закон dN/dt = αN можно считать законом причинным в том смысле, что причины экспоненциального роста – причины внутрисистемные и связаны только с самим этим законом. Действительно, средний коэффициент прироста α = k/τ для каждого организма есть величина постоянная, он может быть равен единице (α = 1), больше единицы (α > 1) и меньше единицы (α < 1).

Прирост популяции за время Δt равен приросту от одного организма, умноженному на численность популяции ΔN/Δt = αN. Рост популяции можно рассматривать как множество параллельных, независимых процессов с относительным сдвигом по фазе, равномерно распределенным на интервале τ.

Каждый организм делится независимо от других, рост определяется лишь эндогенными причинами, все эти причины для каждого организма, делящегося на интервале t – t + Δt, не выходят за пределы этого интервала и представляют собой цепь событий, в которой каждое предшествующее событие является причиной последующего.

* * *

Теперь перейдем к гиперболическому росту. Причинный закон квадратичного роста имеет вид: dN/dt = αN2 = (Nk/τ)N = α'N. Такой рост можно рассматривать как экспоненциальный с переменным, зависящим от общей численности коэффициентом прироста α'. В таком случае общий прирост численности ΔN для всей колонии микроорганизмов может быть получен умножением прироста Δn для одного организма на общую численность N: Δn = α'Δt; ΔN = ΔnN = α'NΔt.

При этом, так же как в предыдущем примере, прирост за характерное время для одной особи может быть гораздо меньшим единицы: Δn << 1. (Можно представить себе микроорганизмы с постоянным α, численность которых хотя и растет экспоненциально, но делятся они чрезвычайно редко; это возможно и при гиперболическом росте на начальном его этапе.)

Если считать закон (1):  dN/dt = αN2 = (Nk/τ)N законом причинным, приходится констатировать, что сам по себе он не в состоянии полностью объяснить гиперболический рост. Действительно, зависимость коэффициента прироста от общей численности N: α' = Nk/τ, выражающая системность растущей популяции, может быть обусловлена лишь какой-то единой, общей для всех организмов причиной.

Эта причина является «сторонней» по отношению к закону (1), никак из него непосредственно не вытекающей. Этим закон (1) отличается от закона (2). Если такая причина, определяющая математическое ожидание прироста для одного организма Δn = α'Δt будет найдена, общий прирост может быть вычислен простым сложением приростов: ΔN = ΔnN.

Но поскольку коэффициент прироста α' зависит от общей численности N, т. е. не есть величина постоянная и меняется со временем, то должен существовать «механизм», обеспечивающий информационную связность, системность растущей популяции, который, собственно, и является истинной причиной гиперболического роста.

Следовательно, закон dN/dt = αN2 (в отличие от причинно-самодостаточного, никем и никак не управляемого закона экспоненциального роста dN/dt = αN) – не может считаться причинным, т. е. не может выступать в качестве причины гиперболического роста. Именно поэтому между этими внешне схожими законами роста популяций лежит непреодолимая пропасть.

Но всегда ли закон экспоненциального роста численности однородных размножающихся «частиц» может считаться причинным законом? Приведем пример экспоненциального роста, для которого закон dN/dt = αN причинным законом считаться не может.

* * *

Рассмотрим производство «универсальных копиров»: фантастических аппаратов, способных создавать точную копию (молекула в молекулу) любого материального объекта (в том числе и самого себя), причем как оригинал, так и копия могут снова себя скопировать.

Будем также считать, что сырье, энергия, рабочие площади присутствуют в неограниченном количестве. Если этим «самовоспроизводством» копиров никто не управляет – рост их будет экспоненциальным, похожим на размножение микроорганизмов в чашке Петри. Элементарное звено причинно-следственной цепи длительностью Δt будет включать здесь события, задаваемые простыми законами с преддетерминацией.

Т. е. величину прироста ΔN определяют события, происходящие в системе на интервале t – t + Δt. Закон dN/dt = αN, полностью определяющий рост производства, в этом случае будет причинным. Представим теперь такую ситуацию. Фирма производитель получает заказ на производство партии копиров. Заказ должен быть выполнен в течение года, и требования заказчика таковы, что это возможно лишь при экспоненциальном росте выпуска продукции, происходящем с максимально возможной скоростью, когда каждый сошедший с конвейера копир сразу же включается в процесс производства как средство производства.

Пусть время снятия копии не является постоянным, а представляет случайную величину с математическим ожиданием и дисперсией. Если производством не управлять, т. е. пустить его на самотек, выход продукции как функция времени будет функцией случайной, близкой к экспоненте, и спустя 12 месяцев будет выпущено некоторое случайное количество копиров. При этом годовой план может быть как перевыполнен, так и недовыполнен.

Введем теперь надстройку: управляющую систему, способную воздействовать на производителя и влиять на скорость производства копиров. (Вопрос о способах воздействия рассматривать здесь не будем.) Допустим, имеются годовой, квартальный и месячный план по производству продукции.

И пусть, к примеру, плановые цифры для всех двенадцати месяцев соответствуют естественному экспоненциальному росту выпуска копиров. Управление требует от производителя четкого выполнения плана, при этом его перевыполнение не приветствуется так же, как и недовыполнение. Т. е. производитель продукции в конце каждого месяца, квартала, года должен в точности выполнить плановое задание с возможным отклонением, скажем, в один процент.