Население Земли как растущая иерархическая сеть

Примером неработающей положительной обратной связи может служить феномен неизменности среднегодовой температуры поверхности Земли в течение сотен миллионов лет. На это обращает внимание венгерский физик теоретик Г. Маркс:

«Температура поверхности Земли определяется тремя факторами – потоком солнечной энергии, отражательной способностью Земли (альбедо) и пропусканием земной атмосферы. Малейшее понижение среднегодовой температуры ведет к увеличению снежного покрова и, как следствие, к понижению альбедо, что ведет к дальнейшему ее понижению. Повышение же температуры приводит к увеличению содержания углекислого газа и водяных паров в атмосфере, что вследствие парникового эффекта еще более ее повышает. Т. е. в обоих случаях имеется самоусиливающийся процесс с положительной обратной связью.

При этом Г. Маркс особо подчеркивает тот факт, что все три фактора от которых зависит температура, меняются со временем, причем различным образом, т. е. положительная обратная связь является стохастической, нерегулируемой (Для гомеостаза необходим непрерывный мониторинг.) Тем не менее температура на поверхности Земли в течение четырех миллиардов лет сохраняется с точностью до 10 %. В условиях положительной обратной связи это требует механизма внешней регулировки. Как же она осуществляется?

Баланс температуры зависит от пропускания атмосферы, которое определяется ее химическим составом, регулируя который можно стабилизировать температуру. При этом состав атмосферы не может меняться произвольным образом, т. к. для поддержания жизни нужен вполне определенный состав. В современной атмосфере Земли, химический состав поддерживается очень точно. Г. Маркс приводит такой пример. Концентрация кислорода в наше время составляет 21 %, если бы она была ниже на 10 %, то не горела бы даже сухая древесина. (При этом не будем забывать какое огромное значение имел огонь для эволюции человека в прошлом и процессы горения без которых не обходится большая часть энергодобывающих технологий в наше время.) Если бы концентрация кислорода была всего на 25 % больше, то горели бы даже сырая трава и лес под дождем, т. е. биосфера вообще не смогла бы существовать.

Но проблема даже не в том, как установилось подобное сочетание параметров (что совершенно непонятно и удивительно), а в том как оно поддерживается в течение сотен миллионов лет. Ведь кислород постоянно воспроизводится в земной атмосфере в процессе фотосинтеза и выводится из нее вследствие процессов горения, дыхания и выветривания. При этом каждую тысячу лет атмосферный кислород полностью обновляется. Какой механизм обеспечивает постоянство концентрации кислорода? Маркс замечает в связи с этим, что термическая и химическая стабильность земной атмосферы скорее похожа на чудо, чем на необходимость.

И вот теперь самое главное – во всех этих рассуждениях не принимался во внимание фактор жизни. По мысли Маргулис и Лавлока именно жизнь выполняет роль регулирующего механизма. Она сама регулирует химический состав и температуру нижних слоев атмосферы. Жизнедеятельность биоты, т. е. всех организмов растительного и животного происхождения, с одной стороны, зависит от состояния биосферы, а, с другой стороны, воздействует на все химические и физические процессы в окружающей среде и, в частности, на процентное содержание атмосферных газов, регулирующих температуру Земли. Например, потепление ведет к росту биомассы, для которой необходим углекислый газ. Снижение процентного содержания углекислоты в атмосфере ведет к уменьшению парникового эффекта и к похолоданию. Существует множество таких регулирующих обратных связей, многие из них не изучены, о некоторых мы даже не подозреваем, причем все они изменяются с течением времени» [22].

Согласно концепции Геи Лавлока, гомеостаз биосферы обеспечивался во все времена эквифинальностью процесса ее эволюции. Эквифинальность здесь означает способность динамической регулирующей системы использовать множество существующих и меняющихся связей в биосфере для обеспечения постоянства среднегодовой температуры и других важных управляемых переменных гомеостаза.

Именно благодаря гомеостазу на планете образовалась жизнь, стала возможной ее эволюция в течение миллиардов лет пока, наконец, не появился человек, появился и всего за несколько тысяч лет социального развития создал ноосферу.

Ноосфера – это результат эволюции биосферы, последняя и высшая ступень в ее развитии. После демографического перехода, происходящего благодаря множеству до конца не изученных причин, «выйдет на полку», стабилизируется (предположительно, в рамках гипотезы) ряд важных показателей глобального развития.

Дальнейшая эволюция станет новым витком спирали, когда будет сохраняться уже гомеостаз ноосферы – высшей стадии развития биосферы; сохраняться благодаря множеству возникающих и исчезающих регулирующих связей самой разнообразной природы. Процесс будет длиться тысячи лет до тех пор, пока в недрах эволюционирующего человечества не возникнет новый вид, средой обитания которого будет уже вся Солнечная система.

Пример причинного закона, объясняющего гипотезу синхронного, гиперболического роста показателей глобального развития

Провозглашение принципа демографического императива или гипотезы синхронного гиперболического роста показателей глобального развития не освобождает еще от необходимости давать объяснение пакету законов на рис. 1. Должен существовать причинный закон, полностью объясняющий парадоксальную независимость важнейших показателей роста и развития от ресурсов.

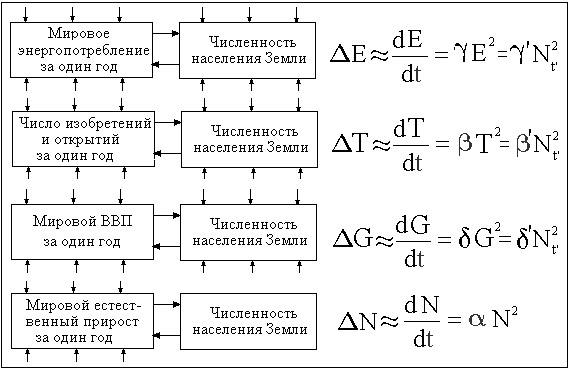
Рис. 1. Рост дифференциальных показателей глобального развития в эпоху гиперболического роста по закону квадратичного роста.

Этот закон должен существовать и в том случае, если связи на рис. 1 не являются причинно-следственными. И все эти функциональные зависимости должны вытекать из этого, неизвестного пока закона. Попробуем сформулировать такой феноменологический закон, причем рассматривать его будем только как пример, как альтернативу неработающему причинному закону квадратичного роста.

Любая феноменологическая теория предполагает введения ряда постулатов. Начнем с определения главного цикла роста и развития, длительность которого равна характерному времени исторических изменений τ = 40 лет. Это время впервые было введено С.П. Капицей в рамках его феноменологической теории гиперболического роста населения Земли.

К сожалению, С.П. Капица не попытался связать его ни с одним из существующих циклических исторических процессов, что, по нашему мнению, является существенным недостатком его модели. Будем считать таким циклическим процессом экономический цикл Кондратьева, который в данной феноменологической схеме определим как главный цикл эволюции и истории.

Второй шаг в определении этого феноменологического закона – разбиение всей эпохи роста от начала неолита (8 тыс. лет до н. э.) до сингулярности гиперболы Фёрстера (2022 год) на 256 циклов. Постулируем относительный прирост населения мира за каждый такой цикл (исключая последний) равным очередному члену гармонической последовательности: 1/255, 1/254… 1/3, 1/2, 1.

Допустим, что численность населения Земли на момент начала неолита была равна 18.5 млн человек. Тогда через 40 лет, т. е. спустя один цикл, эта численность станет равной 18.5 + 18.5/255 = 18.57 млн чел., еще через 40 лет: 18.57+ 18.57/254 = 18.65 млн чел. и т. д.

В результате за 255 циклов, к 1982 году, численность за цикл удвоится и станет равной ее значению на момент начала неолита, умноженному на 256, т. е. примерно 4.74 млрд человек. Причем все 255 ее значений будут лежать на гиперболе Фёрстера.

Сформулируем причинный закон с постдетерминацией, способный объяснить феномен гиперболического роста, в виде принципа эквифинальности роста численности населения Земли:

Гиперболический рост происходит в течение 255 циклов. Зависимость численности и скорости ее роста от времени внутри каждого такого цикла могут быть произвольными при том обязательном условии, что в момент завершения цикла относительный прирост за цикл должен соответствовать очередному члену гармонической последовательности: от 1/255 – до 1.

Говоря о моменте завершения цикла, будем иметь в виду не точку на оси времени, а некоторый интервал в окрестности этой точки, длительность которого гораздо меньше характерного времени τ.

Устойчивость смоделированного здесь роста есть выражение программы эквифинальности по определению. Примером аномальной устойчивости роста может служить последний «гиперболический» 255-й цикл мировой демографической системы (1942–1982 гг.), в течение которого программа эквифинальности вернула, несмотря на значительные потери в двух мировых войнах, рост на «плановую» гиперболу, в результате чего численность за этот цикл удвоилась:

Рис. 1. Возврат кривой роста после двух мировых войн на «плановую» гиперболу.

«– …Вот смотрите: оценки потерь Первой и Второй мировых войн… Мы вернулись на тот же график роста, который был до Первой мировой. Вот кривая роста человечества, тут есть такая выбоина, образованная Первой и Второй мировыми войнами. Но самое главное, что после этого мы не сместились на новую кривую роста, а вернулись на прежнюю. Это очень четко видно.

– Причем в каждой отдельной стране мы наблюдаем демографические волны, связанные с войной, а в целом…

– А в целом она такая вот, как на графике. Если вы вычислите, сколько людей было в этой выбоине, то это даст нам возможность определить полные потери за этот период.

– То есть полные потери: неродившиеся дети нерожденных детей. Не просто физические жертвы, но и потерянные поколения.

– Да. И итоговая цифра потерь оказывается равной 280 млн – в два раза больше, чем интегральные потери, которые оценивались раньше. Раньше давалась цифра в 120 млн, из них 50 млн было убито непосредственно на войне.

– Это странная цифра.

– Вы погодите. Это же оценка для мира в целом, здесь лучше рассуждать не детально. Вы можете сказать, что войны и не было, потому что мы вернулись как бы на прежнюю траекторию. Это был страшный сон такой.

– То есть рана затянулась?

– Да, затянулась. Это поразительный факт. Волны демографические пошли, но они очень постепенно затухают…»[203]

* * *

И, наконец, сформулируем принцип эквифинальности развития системы «все человечество в целом» как обобщение принципа эквифинальности роста численности. (Точно так же как принцип демографического императива Капицы в его «облегченной» формулировке обобщается до закона, «задающего тон» основным показателям развития.)

Интегральные и дифференциальные показатели глобального развития, так же как и численность, должны достигать своего «планового» значения в момент завершения каждого цикла. Рост этих «плановых» значений происходит гиперболически, причем «плановое» значение каждого показателя можно в первом приближении определить умножив постоянный коэффициент на численность в момент завершения цикла для интегрального показателя или на квадрат численности – для дифференциального.

Тот факт, что у гипербол роста этих показателей точки сингулярности различны, можно объяснить, во-первых, недостаточной точностью их определения, т. е. ошибками, связанными с неполнотой и неточностью данных и, во-вторых, возможно, менее строгими требованиями, которые программа эквифинальности предъявляет к их росту в течение цикла. Тем не менее все различия укладываются в интервал, длительность которого не превышает половины характерного времени Капицы.

Кроме эквифинальности по Кондратьевским циклам постулируем также эквифинальность роста и развития по историческим циклам, границы которых можно найти по правилу восьми шагов. Для этого обозначим две точки на оси времени: момент начала неолита, 8 тыс. лет до н. э., и точку сингулярности гиперболы Фёрстера – 2022 год.

Поделим отрезок времени между этими точками пополам, а затем повторим эту процедуру, продвигаясь по оси времени от неолита к точке сингулярности, еще семь раз. Получим восемь периодов исторического развития, причем длительность каждого последующего периода – в два раза меньше предыдущего, а численность на момент его завершения – удваивается.

Программа эквифинальности по историческим циклам может иметь более высокий приоритет, чем по инновационным, хотя это ниоткуда не следует и, кроме того, необходимо еще дать определение приоритету. Не будем пока этого делать и останемся на уровне интуитивного представления. Если Кондратьевский цикл – всего лишь маленький шаг по пути прогресса, то исторический цикл – это уже целая эпоха, на протяжении которой качественно изменяется (причем и генетически тоже) как сам человек, так и социум.

Эквифинальность исторических циклов должна обеспечить «плановый» прогресс во всех областях человеческой деятельности, причем прогресс этот должен быть выражен через поддающиеся измерению показатели глобального развития. Явление сокращения периодов исторического развития полностью соответствует концепции Большой истории, поскольку социальный период эволюции и развития человека и общества есть не что иное, как текущий этап процесса ускоряющейся универсальной эволюции мира от Большого взрыва до наших дней.

И, наконец, завершающий этап программы эквифинальности – это мировой демографический переход. Поскольку переход – это особая, никогда ранее не наблюдавшаяся стадия роста, то как здесь будет работать программа эквифинальности – неизвестно. Скорее всего, в момент завершения второго цикла перехода, в 2062 году, численность населения мира должна будет удвоиться по сравнению с ее значением на момент начала перехода в 1982 году.

* * *

Что же дает принцип эквифинальности роста и развития и чем он лучше принципа демографического императива Капицы? Принцип демографического императива декларирует парадоксальную независимость роста и развития от ресурсов. Эта независимость есть «опытный» факт, факт необъяснимый и противоречащий существующим представлениям о росте численности популяции в условиях ограниченности ресурсов.

Принцип эквифинальности противоречит этим представлениям не более, чем принцип демографического императива Капицы. Но в отличие от принципа Капицы, который вообще ничего не объясняет, принцип эквифинальности объясняет и независимость роста от ресурсов, и гиперболический рост населения мира, и его устойчивость. Гипотеза синхронного гиперболического роста основных показателей глобального развития есть прямое следствие принципа эквифинальности.

Но не слишком ли много постулатов у принципа эквифинальности, не слишком ли велика цена, которую необходимо заплатить за объяснение парадоксов роста? Кроме того – и это нужно признать – такой взгляд на рост и развитие представляется совершенно неправдоподобным. Но какой у нас выбор? Не будем забывать, что принцип демографического императива Капицы опирается на закон квадратичного роста как на причинный закон.

Поверить в то, что закон квадратичного роста определял в эпоху гиперболического роста положительную обратную связь между растущей численностью населения мира и скоростью ее роста – значит поверить в невозможное, чему есть ДЕСЯТЬ представленных нами доказательств (см. далее). И если выбор лежит между неправдоподобным и невозможным, то выбирать следует неправдоподобное. Так поступал и великий сыщик Шерлок Холмс, когда применял свой дедуктивный метод, с помощью которого ему всегда удавалось вычислить преступника:

«Мой старый принцип расследования состоит в том, чтобы исключить все явно невозможные предположения. Тогда то, что остается и является истиной, какой бы неправдоподобной она ни казалась».

Остается, правда, непонятным как Холмс различал тонкую грань между неправдоподобным и невозможным. Но на то он и величайший сыщик всех времен и народов.

Закон квадратичного роста как функциональная, непричинная связь вытекает непосредственно из принципа эквифинальности циклического роста численности. Действительно, поскольку гипербола роста полностью предопределена программой эквифинальности как сеточная функция, то средняя скорость роста за цикл может быть вычислена с помощью закона квадратичного роста.

Миф о технологическом императиве

Российский ученый А.В. Подлазов объясняет гиперболический рост населения Земли ростом жизнесберегающих технологий:

«Необходимыми свойствами обладают только технологии, т. е. знания, которые, будучи однажды обретенными, уже не утрачиваются, так как их распространение и тиражирование дается намного легче, чем создание. Термин «технологии» здесь понимается предельно широко и включает в себя не только способы хозяйствования, но и государственное управление, воинское искусство, религиозные доктрины, средства коммуникаций, торговлю, медицину и вообще любые знания и навыки, которые могут быть использованы для спасения человека от смерти или продления его жизни. Такие знания предлагается именовать жизнесберегающими технологиями» [52].

При этом гипотеза о технологическом императиве опирается на ряд малообоснованных и принципиально непроверяемых положений и содержит множество ошибочных утверждений, которые мы здесь последовательно разберем.

Первое предположение, которое делает Подлазов, заключается в том, что он исключает рост рождаемости из факторов, обеспечивающих рост народонаселения, причем для всех народов, населяющих Землю, и во все времена с момента появления Homo sapience. Рост населения Земли в модели Подлазова, на всем протяжении человеческой истории, происходил лишь за счет уменьшения смертности:

«Таким образом, нет оснований полагать, что рождаемость может систематически увеличиваться. Поэтому мы будем считать ее уровень неизменным в фазе демографического роста и снижающимся во время демографического перехода» [52].

Такую идеализацию принять трудно, несмотря на все оговорки, которые делает Подлазов, поскольку рождаемость, а, следовательно, и ее прирост для разных времен, стран и регионов могла различаться в разы. В наше время, т. е. во время перехода, когда теория Подлазова сохраняет свою силу, рождаемость в странах с мусульманской культурой, численность населения которых составляет четверть населения мира, на десятки процентов превосходит рождаемость в странах с христианской культурой.

Так, в 1989 году на одну мусульманку в мире приходилось 5.2 ребёнка, в то время как на христианку – только 3, в 2000 году эти цифры составляли соответственно 3.7 и 2.6, а в 2010 – 2.9 и 2.6 [17]. И, хотя рождаемость во всех регионах и культурах падает в процессе перехода, но поскольку ее отличие по всем этим регионам и культурам значительно, да и падает она по-разному, – идеализация Подлазова представляется совершенно неприемлемой. Этот же вывод сохраняет свою силу и для эпохи роста, особенно для начального ее этапа.

Далее Подлазов делает сомнительное допущение о том, что суммарный текущий уровень технологий, независимо от природы каждой составляющей этой суммы, может быть охарактеризован одним единственным числом р. Никак конкретно не определяя эту переменную, он тем не менее полагает, что скорость появления новых технологий пропорциональна количеству уже накопленных, а также текущей численности населения Земли: dp/dt ~ pn (4).

Если отождествить суммарный текущий уровень технологий по Подлазову p с уровнем технологического развития цивилизации по Кремеру T, то уравнение (4) есть не что иное, как гипотеза Кузнеца – Кремера dT/dt ~ TN (N =  n – численность населения Земли). На нем основана изобретательская теория Коротаева, хотя Подлазов и предостерегает от чисто изобретательской его трактовки:

«Следует предостеречь от суженной трактовки уравнения (4) как результата исключительно действия «изобретателей» – людей, составляющих определенную часть населения и специализирующихся на совершенствовании технологий. Профессиональная специализация сама по себе является жизнесберегающей технологией, развитие которой и выражается в изменении доли таких людей» [52].

Вопрос о том, почему гипотеза Кузнеца – Кремера, предполагающая причинный характер связи dT/dt ~ TN, является ошибочной, рассмотрен нами далее в п. «Несостоятельность изобретательской теории Коротаева». Те же аргументы, что используются нами для доказательства несостоятельности гипотезы Кузнеца – Кремера dT/dt ~ TN, годятся и для гипотезы Подлазова dp/dt ~ pn.

Считая, что численность населения мира в каждый момент времени определяется созданными к этому моменту технологиями, Подлазов, как и Коротаев, допускает серьезную ошибку, пренебрегая временем запаздывания их распространения по всей Ойкумене:

«…Численность человечества определяется размером созданной им технологической ниши, т. е. тем количеством людей, которые могут быть востребованы созданными ими технологиями: n = f(p); (5). Данное утверждение, постулирующее первичность технологических факторов по отношению к демографическим, назовем технологическим императивом, по аналогии с демографическим императивом, постулировавшим первичность демографии по отношению к экономике, политике, культуре и т. п. Запись формулы (5) в виде алгебраического, а не дифференциального уравнения означает, что при изменении размера ниши подстройка численности происходит очень быстро, поэтому можно считать, что между n и p имеется функциональная связь» [52].

Время «подстройки численности», определяемое текущим размером технологической ниши в технологической модели Подлазова, не является постоянным и зависит от уровня развития социума. В нашей работе это время называется минимально необходимым временем проявления системности. Вопрос о том, почему им нельзя пренебречь ни в какие времена, исключая, возможно, только новейшее, рассмотрен нами ранее в п. «Миф о том, что закон квадратичного роста как причинный закон есть асимптотическая форма более сложного закона, полностью объясняющего рост».

Предположение о масштабируемости человеческих поселений и технологий и, как его следствие, – о степенной зависимости численности от уровня технологического развития, которое делает Подлазов, выводя причинный закон квадратичного роста, представляется выражением крайнего и бессмысленного физикализма:

«И структура технологий, и система расселения людей по своей природе иерархичны, а сами технологии и поселения масштабируемы в диапазоне нескольких порядков величины. Поэтому естественным представляется предположение, что в фазе роста ни одна из входящих в формулу (5) переменных не имеет характерных значений и, следовательно, функция f(p) однородна, т. е. n ~ pγ ; (6). Дифференцирование формулы (6) с последующим исключением переменной p посредством формулы (4) приводит к квадратичной зависимости скорости роста от населения вида (2), ранее полученной на основе анализа демографических данных. Таким образом, данная зависимость оказывается обусловлена технологической природой роста» [52].

Закон степенного роста, как причинный закон роста численности не только популяций, но и любых однородных размножающихся частиц, который выводит Подлазов, исходя из (4) и (5), – никогда не встречается в природе  (см. следующий параграф и параграф «Модель степенного роста, или рассказ о том, как не растут популяции»).

Население Земли многие сотни лет росло по закону гиперболы – это неоспоримый факт. Но рост населения отдельных стран и регионов, как мы это неоднократно подчеркивали, не мог быть гиперболическим, поскольку при прочих равных условиях квадрат суммы не равен сумме квадратов. Однако Подлазов так не считает:

«Исключение из системы (8) – (9) не численности населения n, а константы C дает уравнение dn/dt = pn, объясняющее, почему гиперболический закон вида n = C/(tf – t)) оказывается, по крайней мере, приближенно применим к численности населения не только всего мира, но также отдельных регионов и даже стран. Если с некоторой точностью можно считать, что они характеризуются тем же самым технологическим уровнем p, что и мир в целом, то для них скорость роста населения линейно зависит от его численности с одним и тем же коэффициентом p = 1/(tf – t). Более того, применимость закона вида N =C/(tf – t) к частям мира сохраняется даже в том случае, если их технологический уровень составляет неизменную долю от общемирового, т. е. если они отстают в развитии, но отстают равномерно» [52].

Действительно, если в уравнение dn/dt = pn чисто формально подставить p = 1/(tf – t) и проинтегрировать, то получим n = C/(tf – t). Однако такой формализм предполагает не просто одинаковый, а меняющийся по одному и тому же гиперболическому закону уровень технологического развития разных стран, регионов и мира в целом. Можно ли в такое поверить?