Заметки в инвестировании. Книга об инвестициях и управлении капиталом. 5-е издание, переработанное и дополненное

Еще один важный параметр – срок до погашения. Возьмем, например, облигацию со сроком погашения 1 год и текущей стоимостью 80% от номинала. Дисконт равен 20%, а доходность такой облигации составляет 25% годовых (20/80 * 100% = 25%).

Главный параметр, который влияет на стоимость облигаций, – это общий уровень процентных ставок. Когда уровень ставок растет, растет доходность, которую хотят получить инвесторы при вложении в облигации => увеличивается дисконт => падает цена облигации. При снижении процентных ставок все происходит наоборот: инвесторы готовы довольствоваться меньшей доходностью => уменьшается дисконт => растут цены на облигации.

Если предположить, что доходность нашей облигации точно соответствует уровню процентных ставок, можно увидеть, как будет меняться ее стоимость в зависимости от этого параметра.

Поэтому для эффективного управления портфелем облигаций важно уметь точно прогнозировать будущий уровень процентных ставок.

При неизменном уровне процентных ставок с течением времени стоимость облигации будет плавно приближаться к номинальной стоимости. В идеальном случае график текущих цен будет выглядеть как почти прямая линия или, точнее, слегка выпуклая вверх дуга. В случае нашей облигации, если процентные ставки будут сохраняться на уровне 25%, ее стоимость через полгода будет составлять примерно 89% от номинала, а дисконт 11%.

Формула для расчета доходности облигации к погашению выглядит так:

Но если общий уровень процентных ставок будет падать, цена на облигацию будет расти быстрее. И наоборот, при росте процентных ставок цена на облигацию будет расти медленнее или (при значительном росте) может даже временно снизиться. В приведенной выше таблице показано, какой будет цена нашей облигации через полгода при разном уровне процентных ставок. Мы видим, что если уровень процентных ставок вырастет до 50% годовых, цена нашей облигации останется на том же уровне, что и полгода назад, то есть не принесет владельцу за это время никакой выгоды. Но в случае снижения процентных ставок владелец облигации получит за эти полгода гораздо большую доходность, чем изначально рассчитывал. Допустим для простоты, что номинальная стоимость облигации 100 ₽. Вложив 80 ₽, владелец облигации получит за полгода 15,3 ₽, что означает доходность облигации 38,25% годовых вместо ожидаемых 25%.

Формула для расчета доходности облигации от владения выглядит так:

Цена облигаций с разным сроком до погашения при изменении уровня процентных ставок будет меняться по-разному. Цена облигаций с большим сроком до погашения более чувствительна к изменению уровня процентных ставок.

Отсюда вытекает простое правило: при ожидаемом снижении уровня процентных ставок более выгодно покупать «длинные» облигации с большим сроком до погашения. При ожидании роста процентных ставок лучше покупать «короткие» облигации.

УК Арсагера постоянно анализирует уровень процентных ставок и рассчитывает вектор процентных ставок для государственных, корпоративных и муниципальных облигаций. Этот показатель характеризует наши ожидания по изменению процентных ставок в ближайший год. Положительный вектор процентных ставок означает ожидание роста общего уровня процентных ставок и снижение цен на облигации. По нашему мнению, при положительном векторе процентных ставок целесообразно покупать «короткие» облигации. При отрицательном, наоборот, «длинные».

Значение вектора по модулю характеризует силу изменения уровня процентных ставок по облигациям в течение ближайшего года. Например, вектор процентных ставок +20% означает, что мы ожидаем роста процентных ставок по облигациям на 20%. При текущем уровне процентных ставок, скажем 10%, это будет означать, что мы ожидаем их роста до 12%.

Формирование портфеля облигаций

Теперь, когда мы объяснили механизм формирования цены и управления доходностью, скажем несколько слов о формировании портфеля и сравнении облигаций между собой. Все облигации, которые обращаются на рынке, разные. Мы делим все множество облигаций на однородные по мере риска группы, используя систему ранжирования Arsagera Asset Certification. При ранжировании учитываются такие показатели, как ликвидность и кредитное качество. Первая и вторая группы – это наиболее надежные и ликвидные облигации, третья и четвертая – второй эшелон, пятая и шестая – высокорисковые облигации. Каждый инвестор формирует портфель с учетом собственного аппетита и отношения к риску.

УК Арсагера в рамках каждой группы, так же как и при управлении портфелем акций, строит хит-парад облигаций по потенциальной доходности. Для каждой облигации рассчитывается потенциальная доходность с учетом текущей стоимости, будущей стоимости (прогнозируемой с учетом наших ожиданий по изменению уровня процентных ставок), промежуточных выплат и оферт (обязательств эмитента по досрочному погашению).

В рамках инвестиционной декларации устанавливаются лимиты на каждую группу облигаций и на одного эмитента в каждой группе. Таким образом, устанавливаются требования к диверсификации. Задача компании – сформировать и поддерживать в портфеле набор облигаций, имеющих максимальную потенциальную доходность, а также изменять структуру портфеля при изменении уровня процентных ставок.

Выводы

•      При ожидаемом снижении уровня процентных ставок более выгодно покупать «длинные» облигации, а при ожидании роста – «короткие».

•      Необходимо выбрать меру риска для портфеля облигаций, которая соответствует вашему аппетиту к риску. При выполнении данной задачи вы можете использовать систему ранжирования Arsagera Asset Certification.

Два этих ↑ простых совета помогут вам самостоятельно сформировать портфель облигаций и эффективно им управлять.

•      Для повышения эффективности управления портфелем необходимо сравнивать облигации между собой в рамках каждой группы, а также рассчитывать и постоянно отслеживать их потенциальную доходность. Это трудоемкий процесс, который мы можем выполнить для вас в рамках управления портфелем облигаций.

Следующий материал курса «Университет»: 9.8. Как инвестировать в акции, используя потенциальную доходность?

9.8. Как инвестировать в акции, используя потенциальную доходность? (Курс «Университет»)

Когда вы приходите в банк положить деньги на депозит, вы смотрите на доходность, которую установил банк и которую вы получите в будущем. Вас не интересует, какие проценты получили люди, которые принесли в банк деньги год назад. И это абсолютно здравый и правильный подход к размещению денег на депозите.

Когда речь идет о покупке акций, людям кажется, что информация о том, сколько принесло владение той или иной акцией тем, кто купил ее год (месяц, неделю, день) назад, влияет на то, сколько владение этой акцией принесет им. На похожей идее основывается технический анализ, главный постулат которого – вся информация о будущих ценах содержится в графике, отражающем прошлые изменения цен.

Однако к покупке акций можно подходить так же как к банковскому депозиту – покупать те акции, которые обладают более высокой доходностью. Но на акциях не написана их будущая доходность, поэтому мы называем этот показатель «потенциальная доходность». Такое название отражает вероятностный характер получения доходности.

Расчет потенциальной доходности акций

Как узнать потенциальную доходность от инвестирования в акции? Расчет очень простой: есть текущая цена, есть период времени (например, год) и есть будущая цена (через год). Разница между будущей и текущей ценой и отражает потенциальный результат за период. Самый сложный и трудоемкий процесс – это сделать прогноз будущих цен акций. Мы рассчитываем будущие цены исходя из фундаментальных показателей деятельности бизнеса (прибыли, выручки, балансовой стоимости и пр.).

После того, как сделаны все расчеты, мы получаем потенциальную доходность по всем акциям и можем отсортировать полученный список исходя из размера потенциальной доходности каждой из акций. У нас получится своеобразный хит-парад акций.

Как управлять портфелем акций, используя хит-парад?

При управлении портфелем мы ставим перед собой задачу обеспечивать максимальную потенциальную доходность портфеля при заданном клиентом уровне риска.

Если у клиента четко сформированы его инвестиционные приоритеты, то при передаче средств в управление он составляет инвестиционную декларацию, в которой задает определенный уровень риска портфеля. Если у инвестора нет индивидуальных требований к инвестиционной декларации, то он может «присоединиться» к портфелю инвестиционного фонда, в котором существует своя, общая для всех инвесторов декларация (регламент управляющего трейдера).

В инвестиционной декларации устанавливаются требования и ограничения к составу и структуре портфеля. В частности, она позволяет установить соотношение акций и облигаций в портфеле, лимиты на каждую группу ценных бумаг, лимиты на одного эмитента в каждой группе.

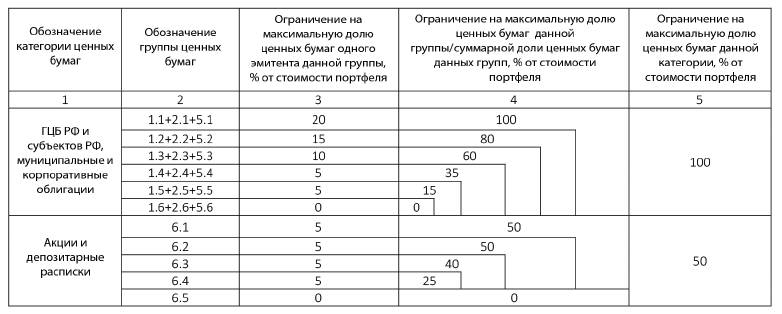
В инвестиционной декларации, которую мы используем для примера, установлен лимит на долю акций в портфеле в 50%. Это означает, что когда рынок акций растет и доля акций в портфеле увеличивается, соблюдение выбранного соотношения акций и облигаций приводит к необходимости продать небольшую часть акций. При снижении рынка акций, наоборот, увеличивается доля облигаций. Тогда продается часть облигаций и приобретаются акции. Это, как правило, позволяет продавать некоторую часть акций по более высоким ценам и покупать по более низким. В то же время строго соблюдается мера риска, установленная клиентом в инвестиционной декларации.

Перейдем теперь на уровень отдельных акций. В нашем примере лимит на группу 6.4 составляет 25%, а лимит на одну акцию в этой группе – 5% (3-й и 4-й столбцы в таблице). Это означает, что соблюдая установленные клиентом требования к диверсификации и максимизируя потенциальную доходность, в портфель будут приобретены 5 акций (25%/5%) с вершины хит-парада.

Однако цены акций, входящих в портфель, меняются неравномерно. Какие-то акции растут быстрее, увеличивается их доля в портфеле, но при этом снижается их потенциальная доходность. Другие акции, входящие в портфель, растут медленнее или даже падают (что приводит к росту потенциальной доходности). Для соблюдения установленных лимитов (долей в портфеле) часть выросших акций продается для того, чтобы соблюдать требование декларации. На вырученные деньги приобретаются те бумаги, доля которых снизилась. Если в последующем цена выросших акций снижается, – снижается их доля в портфеле и восстанавливается потенциальная доходность. Необходимое количество акций для восстановления доли вновь приобретается в портфель, для этого из портфеля продаются бумаги с наименьшей потенциальной доходностью. Это позволяет дополнительно повышать эффективность портфеля при резких колебаниях стоимости акций, находящихся в портфеле. Процесс восстановления доли актива в портфеле называется ребалансировкой.

Обратите внимание, что продается не весь пакет данных акций, а только корректируется их доля в портфеле. Определенная акция продается из портфеля полностью только в том случае, если в хит-параде появляются другие, более потенциально доходные.

Похожие эффекты возникают и при соблюдении лимитов на группы (4-й столбик в таблице), но здесь нужно пояснение. В нашем примере лимит на группу 6.4 – 25%, а следующий лимит (40%) устанавливается суммарно на группы 6.3 и 6.4. Это выражено в таблице объединяющим «уголком».

В портфель может быть приобретено 8 (40%/5%) эмитентов из групп 6.3 и 6.4 с максимальной потенциальной доходностью, но не более 5 (25%/5%) из группы 6.4.

Легендарный инвестор Уоррен Баффет сказал: «Лучшее время для продажи акций – никогда». Мы полагаем, что он имел в виду акции как класс активов, а не акции конкретного эмитента, поэтому можно развить эту мысль так: «лучшее время для продажи акций – когда найдены другие, более потенциально доходные». Мы используем именно такой подход.

Вывод

•      При управлении портфелем акций надо следить за изменением хит-парада, продавать акции, которые ушли с лидирующих позиций, и покупать новых лидеров. То есть держать в портфеле набор акций с максимальной потенциальной доходностью и соблюдать диверсификацию, которая установлена инвестиционной декларацией. При этом соблюдается важное правило – вы всегда владеете акциями.

Следующий материал курса «Университет»: 9.9. Как рассчитать доходность? Метод Арсагеры

9.9. Как рассчитать доходность? Метод Арсагеры (Курс «Университет») UPD

На первый взгляд, дать ответ на этот вопрос несложно. Многие знают: чтобы посчитать доходность, необходимо результат инвестиций разделить на сумму вложенных средств и перевести полученное значение в годовые проценты.

Формула расчета доходности (в годовых процентах), если не происходило вводов/выводов:

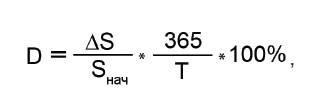
где D – искомая доходность;

∆S – результат инвестирования;

Sнач – сумма первоначальных инвестиций;

T – количество дней в рассматриваемом периоде.

Но задача расчета доходности многократно усложняется в случае, если в течение рассматриваемого периода осуществлялись вводы и/или выводы средств в рамках инвестиционного портфеля. В таком виде она вызывает затруднения даже у опытных специалистов в области инвестиций. Кроме того, не существует идеального способа подсчета доходности в этом случае, поэтому необходимо согласиться (и хорошо их понимать) с определенными допущениями, которые используются в том или ином методе. Мы предлагаем свое решение данной задачи. Сравнение нашего метода с другими известными способами подсчета доходности будет приведено в отдельном материале.

Начнем с определения того, что же такое вводы и выводы денежных средств. Ввод денежных средств – это направление денег на инвестиции. К примеру, вы приобрели инвестиционные паи фонда или внесли деньги на брокерский счет – все это является вводом средств. Изъятие инвестиционных средств является выводом средств, то есть в наших примерах выводы возникают при погашении инвестиционных паев или выводе денег с брокерского счета.

Зная, что же такое вводы/выводы средств, рассмотрим конкретную ситуацию, которая поможет понять логику решения задачи по корректному определению доходности с учетом вводов/выводов средств.

1. Некий инвестор приобрел акций на сумму в 1 000 ₽ (Sнач).

2. Через 3 месяца он купил еще акций на 500 ₽ (Sвв).

3. Еще через 4 месяца инвестору срочно понадобились деньги, и он был вынужден продать часть акций на сумму в 300 ₽ (Sвыв).

4. Через год после первоначального приобретения, стоимость акций составила 1 300 ₽ (Sитог).

В виде графика данную ситуацию можно представить следующим образом:

Чтобы корректно рассчитать доходность от инвестиций, нам по-прежнему необходимо разделить результат инвестиций на сумму вложенных средств. Остается только определить, что в рассматриваемой ситуации является результатом и какова корректная сумма вложенных средств.

Первый шаг будет расчет результата инвестиций. И в этом отношении нет никакой сложности, кроме того, финансовый результат вычисляется абсолютно точно. Результат инвестиций – это разница между тем, что мы вывели и имеем на конец периода, и тем, что было вложено. То есть необходимо из суммы стоимости инвестиций на конец периода и всех выводов за период вычесть сумму начального и всех последующих вводов.

Формула для определения результата инвестирования с учетом вводов/выводов:

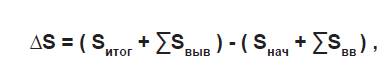
∆S = ( Sитог + ∑Sвыв ) – ( Sнач + ∑Sвв ) ,

где ∆S – результат инвестирования за период в абсолюте;

Sитог – итоговая оценка инвестиций (1 300);

∑Sвыв – сумма всех выводов средств (300);

Sнач – сумма первоначальных инвестиций (1 000);

∑Sвв – сумма всех вводов средств (500).

Применим данную формулу к рассмотренной ситуации:

ΔS = (1 300 + 300) – (1 000 + 500) = 100.

Таким образом, инвестор заработал 100 ₽.

Второй шаг в расчете доходности является наиболее важным: необходимо корректно определить, с какой суммой соотносить рассчитанный результат инвестирования. А еще точнее, вычислить размер средств в виде единой суммы, которой инвестор как бы оперировал в течение всего периода.

Есть любители считать сумму вложенных средств без учета денег, которые были введены на счет (брокерский), но на которые не приобретались ценные бумаги. Такой расчет может резко завысить доходность, хотя прибыль по инвестициям от этого не увеличится. Этот расчет неверен, денежная составляющая инвестиционного портфеля при расчете суммы вложенных средств должна учитываться в полном объеме. Неверно рассчитывать доходность только на часть портфеля, ведь средства, введенные на счет, отвлечены от других целей (потребления, накопления и др.) и являются инвестициями, доходность которых и необходимо узнать.

Необходимо согласиться со следующей логикой: в каждый временной подпериод сумма, которой оперировал инвестор, была разной. Начальная сумма была «рабочей» до первого момента ввода или вывода, затем, чтобы понять «рабочую» сумму на следующем подпериоде, её нужно скорректировать на размер ввода (увеличить) или вывода (уменьшить), и так далее для каждого подпериода до конца срока, за который считается доходность.

В подпериод T1: 1 000 ₽, T2: (1 000 + 500) ₽, T3: (1 000 + 500 – 300) ₽. Кроме того, сами по себе эти временные подпериоды не равны. T1 = 90 дней, T2 = 120 дней, T3 = 155 дней. Поэтому необходимо взвесить соответствующую «рабочую» сумму на количество дней в подпериоде, определив таким образом единую средневзвешенную по времени «рабочую» сумму на всем рассматриваемом периоде.

Формула для определения средневзвешенной суммы вложенных средств с учетом вводов/выводов:

где V – средневзвешенная сумма;

T1, T2, T3, …, Tn – количество дней в подпериоде;

∑Ti – суммарное количество дней на рассматриваемом временном отрезке.

Применим данную формулу к рассмотренной ситуации:

V = (90 * 1 000 + 120 * (1 000 + 500) + 155 * (1 000 + 500 – 300))/365 = 1 249,32

Средневзвешенная сумма вложенных инвестором средств – 1 249,32 ₽.

Теперь известны все элементы, необходимые для непосредственного расчета доходности.

Если вы хотите рассчитать доходность за период, который не включает в себя первоначальный ввод средств, то за Sнач необходимо принять стоимость инвестиционного портфеля на ту дату, с которой вы хотите начать расчет доходности.

Третий шаг – расчет доходности из полученных значений. Для этого поделим рассчитанный ранее результат инвестирования на средневзвешенную сумму вложенных средств и переведем полученный результат в годовые проценты:

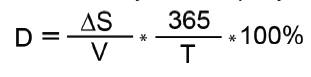
Получается, что в рассмотренной ситуации доходность составляет:

(100 / 1 249,32) * 365 / 365 * 100% = 8% годовых.

Это аналогично тому, что у инвестора не было никаких вводов/выводов, и он просто в самом начале вложил сумму в размере 1 249,32 ₽, весь период ей оперировал, а в итоге получил прибыль в размере 100 ₽.

Также можно использовать формулу, учитывающую сложный процент:

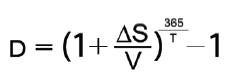
Используя данные формулы, вы всегда сможете корректно оценить доходность вашего инвестиционного портфеля и при помощи полученных значений оценить эффективность ваших инвестиций.

Теперь рассмотрим некоторые нестандартные случаи, с которыми можно столкнуться на практике (у нас они случались не раз).

1-й вырожденный случай

Рассмотрим следующий пример:

Ввели 1 000 ₽, спустя 3 месяца наши инвестиции утроились (вот такая удача!), что позволило нам вывести 2000 ₽, затем через 7 месяцев мы ввели сумму 1100 ₽, а по окончании года с момента начала инвестиций стоимость нашего портфеля составила 1300 ₽. Таким образом, прибыль за весь срок:

ΔS = (1 300 + 2 000) – (1 000 + 1 100) = 1 200

С оценкой прибыли проблем никаких нет – здесь все корректно, как и произошло на практике.

V = (90 * 1 000 + 120 * (1 000 – 2 000) + 155 * (1 000 – 2 000 + 1 100))/365 =

= (90 * 1 000 + 120 * (-1 000) + 155 * 100)/365 = –39,73

А вот с расчетом средневзвешенной рабочей суммы возникают сложности. На втором временном отрезке сумма получается отрицательная (– 1 000). Вес ее настолько велик, что и вся средневзвешенная сумма на периоде получается отрицательной.

Корректно оценить размер полученной доходности не получается. Поэтому мы доработали наш метод. В таких случаях, отрицательные суммы, получившиеся на определенных временных отрезках, делаем равными нулю (считаем, что работа ведется заработанной ранее прибылью, то есть нулевой рабочей суммой на этом подпериоде). Как следствие, если:

Таким образом, в данном примере:

V = (90 * 1 000 + 120 * (1 000 – 2 000) + 155 * (1 000 – 2 000 + 1 100))/365 = (90 * 1 000 + 120 * 0 + 155 * 100)/365 = 289,04

Далее

D = (ΔS/V) * 365/T * 100% = (1 200/289,04) * 365/365 * 100% = 415,17% годовых.

Или D = (1 + (ΔS/V))365/T – 1 = (1 + (1 200/289,04))365/365 – 1 = 4,1517 то есть 415,17% годовых.

Данный результат, на наш взгляд, является значительно более правдоподобным.

2-й вырожденный случай

Предположим, Вы осуществляете регулярные инвестиции и в начале каждого квартала в течение 2 лет вносите определенную сумму, например, 1 000 ₽. Таким образом вы внесли 8 000 ₽ за весь период. Несложно посчитать, что средневзвешенная рабочая сумма на этом периоде составит 4 500 ₽.

Например, на рынке случился грандиозный обвал (так было в конце 2008 года), и стоимость Вашего портфеля на конец периода составила 3 000 ₽. Рассчитаем доходность таких инвестиций:

ΔS = 3 000 – 8 000 = – 5 000

Таким образом, отрицательная переоценка больше половины внесенных средств и, что особенно важно, превышает размер средневзвешенной рабочей суммы 5 000 > 4 500. Тогда расчет по формуле:

D = (1 + (ΔS/V))365/T – 1, становится невозможен!

D = (1 + (–5 000/4 500))365/730 – 1, так как отсутствует математическая возможность вычисления квадратного корня из отрицательного числа.

Действительно, ситуация выглядит несколько абсурдно, так как потери как бы превышают рабочую сумму. При этом, естественно, потери не больше суммы всех внесенных средств.