 Полная версия
Полная версияOn the Philosophy of Discovery, Chapters Historical and Critical
The assertion of a Faculty of the mind by which it apprehends Truth, which Faculty is higher than the Discursive Reason, as the Truth apprehended by it is higher than mere Demonstrative Truth, agrees (as it will at once occur to several of my readers) with the doctrine taught and insisted upon by the late Samuel Taylor Coleridge. And so far as he was the means of inculcating this doctrine, which, as we see, is the doctrine of Plato, and I might add, of Aristotle, and of many other philosophers, let him have due honour. But in his desire to impress the doctrine upon men's minds, he combined it with several other tenets, which will not bear examination. He held that the two Faculties by which these two kinds of truth are apprehended, and which, as I have said, our philosophical writers call the Intuitive Reason and the Discursive Reason, may be called, and ought to be called, respectively, The Reason and The Understanding; and that the second of these is of the nature of the Instinct of animals, so as to be something intermediate between Reason and Instinct. These opinions, I may venture to say, are altogether erroneous. The Intuitive Reason and the Discursive Reason are not, by any English writers, called the Reason and the Understanding; and accordingly, Coleridge has had to alter all the passages, namely, those taken from Leighton, Harrington, and Bacon, from which his exposition proceeds. The Understanding is so far from being especially the Discursive or Reasoning Faculty, that it is, in universal usage, and by our best writers, opposed to the Discursive or Reasoning Faculty. Thus this is expressly declared by Sir John Davis in his poem On the Immortality of the Soul. He says, of the soul,
When she rates things, and moves from ground to ground,The name of Reason (Ratio) she acquires from this:But when by reason she truth hath found,And standeth fixt, she Understanding is.Instead of the Reason being fixed, and the Understanding discursive, as Mr. Coleridge says, the Reason is distinctively discursive; that is, it obtains conclusions by running from one point to another. This is what is meant by Discursus; or, taking the full term, Discursus Rationis, Discourse of Reason. Understanding is fixed, that is, it dwells upon one view of a subject, and not upon the steps by which that view is obtained. The verb to reason, implies the substantive, the Reason, though it is not coextensive with it: for as I have said, there is the Intuitive Reason as well as the Discursive Reason. But it is by the Faculty of Reason that we are capable of reasoning; though undoubtedly the practice or the pretence of reasoning may be carried so far as to seem at variance with reason in the more familiar sense of the term; as is the case also in French. Moliere's Crisale says (in the Femmes Savantes),
Raisonner est l'emploi de toute ma maison,Et le raisonnement en bannit la Raison.If Mr. Coleridge's assertion were true, that the Understanding is the discursive and the Reason the fixed faculty, we should be justified in saying that The Understanding is the faculty by which we reason, and the Reason is the faculty by which we understand. But this is not so.
Nor is the Understanding of the nature of Instinct, nor does it approach nearer than the Reason to the nature of Instinct, but the contrary. The Instincts of animals bear a very obscure resemblance to any of man's speculative Faculties; but so far as there is any such resemblance, Instinct is an obscure image of Reason, not of Understanding. Animals are said to act as if they reasoned, rather than as if they understood. The verb understand is especially applied to man as distinguished from animals. Mr. Coleridge tells a tale from Huber, of certain bees which, to prevent a piece of honey from falling, balanced it by their weight, while they built a pillar to support it. They did this by Instinct, not understanding what they did; men, doing the same, would have understood what they were doing. Our Translation of the Scriptures, in making it the special distinction of man and animals, that he has Understanding and they have not, speaks quite consistently with good philosophy and good English.
Mr. Coleridge's object in his speculations is nearly the same as Plato's; namely, to declare that there is a truth of a higher kind than can be obtained by mere reasoning; and also to claim, as portions of this higher truth, certain fundamental doctrines of Morality. Among these, Mr. Coleridge places the Authority of Conscience, and Plato, the Supreme Good. Mr. Coleridge also holds, as Plato held, that the Reason of man, in its highest and most comprehensive form, is a portion of a Supreme and Universal Reason; and leads to Truth, not in virtue of its special attributes in each person, but by its own nature.
Many of the opinions which are combined with these doctrines, both in Plato and in Coleridge, are such as we should, I think, find it impossible to accept, upon a careful philosophical examination of them; but on these I shall not here dwell.
I will only further observe, that if any one were to doubt whether the term Νοῦς is rightly rendered Intuitive Reason, we may find proof of the propriety of such a rendering in the remarkable discussion concerning the Intellectual Virtues, which we have in the Sixth Book of the Nicomachean Ethics. It can hardly be questioned that Aristotle had in his mind, in writing that passage, the doctrines of Plato, as expounded in the passage just examined, and similar passages. Aristotle there says that there are five Intellectual Virtues, or Faculties by which the Mind aims at Truth in asserting or denying:—namely, Art, Science, Prudence, Wisdom, Nous. In this enumeration, passing over Art, Prudence, and Wisdom, as virtues which are mainly concerned from practical life, we have, in the region of speculative Truth, a distinction propounded between Science and Nous: and this distinction is further explained (c. 6) by the remarks that Science reasons with Principles; and that these Principles cannot be given by Science, because Science reasons from them; nor by Art, nor Prudence, for these are conversant with matters contingent, not with matters demonstrable; nor can the First Principles of the Reasonings of Science be given by Wisdom, for Wisdom herself has often to reason from Principles. Therefore the First Principles of Demonstrative Reasoning must be given by a peculiar Faculty, Nous. As we have said, Intuitive Reason is the most appropriate English term for this Faculty.
The view thus given of that higher kind of Knowledge which Plato and Aristotle place above ordinary Science, as being the Knowledge of and Faculty of learning First Principles, will enable us to explain some expressions which might otherwise be misunderstood. Socrates, in the concluding part of this Sixth Book of the Republic, says, that this kind of knowledge is "that of which the Reason (λόγος) takes hold, in virtue of its power of reasoning348." Here we are plainly not to understand that we arrive at First Principles by reasoning: for the very opposite is true, and is here taught;—namely, that First Principles are not what we reason to, but what we reason from. The meaning of this passage plainly is, that First Principles are those of which the Reason takes hold in virtue of its power of reasoning;—they are the conditions which must exist in order to make any reasoning possible:—they are the propositions which the Reason must involve implicitly, in order that we may reason explicitly;—they are the intuitive roots of the dialectical power.
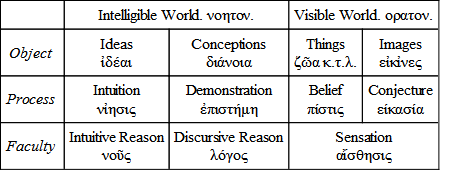
In accordance with the views now explained, Plato's Diagram may be thus further expanded. The term ιδέα is not used in this part of the Republic; but, as is well known, occurs in its peculiar Platonic sense in the Tenth Book.
The Cambridge Philosophical Society has willingly admitted among its proceedings not only contributions to science, but also to the philosophy of science; and it is to be presumed that this willingness will not be less if the speculations concerning the philosophy of science which are offered to the Society involve a reference to ancient authors. Induction, the process by which general truths are collected from particular examples, is one main point in such philosophy: and the comparison of the views of Induction entertained by ancient and modern writers has already attracted much notice. I do not intend now to go into this subject at any length; but there is a cardinal passage on the subject in Aristotle's Analytics, (Analyt. Prior. II. 25) which I wish to explain and discuss. I will first translate it, making such emendations as are requisite to render it intelligible and consistent, of which I shall afterwards give an account.
I will number the sentences of this chapter of Aristotle in order that I may afterwards be able to refer to them readily.
§ 1. "We must now proceed to observe that we have to examine not only syllogisms according to the aforesaid figures,—syllogisms logical and demonstrative,—but also rhetorical syllogisms,—and, speaking generally, any kind of proof by which belief is influenced, following any method.
§ 2. "All belief arises either from Syllogism or from Induction: [we must now therefore treat of Induction.]
§ 3. "Induction, and the Inductive Syllogism, is when by means of one extreme term we infer the other extreme term to be true of the middle term.
§ 4. "Thus if A, C, be the extremes, and B the mean, we have to show, by means of C, that A is true of B.
§ 5. "Thus let A be long-lived; B, that which has no gall-bladder; and C, particular long-lived animals, as elephant, horse, mule.
§ 6. "Then every C is A, for all the animals above named are long-lived.
§ 7. "Also every C is B, for all those animals are destitute of gall-bladder.
§ 8. "If then B and C are convertible, and the mean (B) does not extend further than extreme (C), it necessarily follows that every B is A.
§ 9. "For it was shown before, that, if any two things be true of the same, and if either of them be convertible with the extreme, the other of the things predicated is true of the convertible (extreme).
§ 10. "But we must conceive that C consists of a collection of all the particular cases; for Induction is applied to all the cases.
§ 11. "But such a syllogism is an inference of a first truth and immediate proposition.
§ 12. "For when there is a mean term, there is a demonstrative syllogism through the mean; but when there is not a mean, there is proof by Induction.
§ 13. "And in a certain way, Induction is contrary to Syllogism; for Syllogism proves, by the middle term, that the extreme is true of the third thing: but Induction proves, by means of the third thing, that the extreme is true of the mean.
§ 14. "And Syllogism concluding by means of a middle term is prior by nature and more usual to us; but the proof by Induction, is more luminous."
I think that the chapter, thus interpreted, is quite coherent and intelligible; although at first there seems to be some confusion, from the author sometimes saying that Induction is a kind of Syllogism, and at other times that it is not. The amount of the doctrine is this.
When we collect a general proposition by Induction from particular cases, as for instance, that all animals destitute of gall-bladder (acholous), are long-lived, (if this proposition were true, of which hereafter,) we may express the process in the form of a Syllogism, if we will agree to make a collection of particular cases our middle term, and assume that the proposition in which the second extreme term occurs is convertible. Thus the known propositions are
Elephant, horse, mule, &c., are long-lived.
Elephant, horse, mule, &c., are acholous.
But if we suppose that the latter proposition is convertible, we shall have these propositions:
Elephant, horse, mule, &c., are long-lived.
All acholous animals are elephant, horse, mule, &c.,
from whence we infer, quite rigorously as to form,
All acholous animals are long-lived.
This mode of putting the Inductive inference shows both the strong and the weak point of the illustration of Induction by means of Syllogism. The strong point is this, that we make the inference perfect as to form, by including an indefinite collection of particular cases, elephant, horse, mule, &c., in a single term, C. The Syllogism then is
All C are long-lived.
All acholous animals are C.
Therefore all acholous animals are long-lived.
The weak point of this illustration is, that, at least in some instances, when the number of actual cases is necessarily indefinite, the representation of them as a single thing involves an unauthorized step. In order to give the reasoning which really passes in the mind, we must say
Elephant, horse, &c., are long-lived.
All acholous animals are as elephant, horse, &c.,
Therefore all acholous animals are long-lived.
This "as" must be introduced in order that the "all C" of the first proposition may be justified by the "C" of the second.
This step is, I say, necessarily unauthorized, where the number of particular cases is indefinite; as in the instance before us, the species of acholous animals. We do not know how many such species there are, yet we wish to be able to assert that all acholous animals are long-lived. In the proof of such a proposition, put in a syllogistic form, there must necessarily be a logical defect; and the above discussion shows that this defect is the substitution of the proposition, "All acholous animals are as elephant, &c.," for the converse of the experimentally proved proposition, "elephant, &c., are acholous."
In instances in which the number of particular cases is limited, the necessary existence of a logical flaw in the syllogistic translation of the process is not so evident. But in truth, such a flaw exists in all cases of Induction proper: (for Induction by mere enumeration can hardly be called Induction). I will, however, consider for a moment the instance of a celebrated proposition which has often been taken as an example of Induction, and in which the number of particular cases is, or at least is at present supposed to be, limited. Kepler's laws, for instance the law that the planets describe ellipses, may be regarded as examples of Induction. The law was inferred, we will suppose, from an examination of the orbits of Mars, Earth, Venus. And the syllogistic illustration which Aristotle gives, will, with the necessary addition to it, stand thus,
Mars, Earth, Venus describe ellipses.
Mars, Earth, Venus are planets.
Assuming the convertibility of this last proposition, and its universality, (which is the necessary addition in order to make Aristotle's syllogism valid) we say
All the planets are as Mars, Earth, Venus.
Whence it follows that all the planets describe ellipses.
If, instead of this assumed universality, the astronomer had made a real enumeration, and had established the fact of each particular, he would be able to say
Saturn, Jupiter, Mars, Earth, Venus, Mercury, describe ellipses.
Saturn, Jupiter, Mars, Earth, Venus, Mercury are all the planets.
And he would obviously be entitled to convert the second proposition, and then to conclude that
All the planets describe ellipses.
But then, if this were given as an illustration of Induction by means of syllogism, we should have to remark, in the first place, that the conclusion that "all the planets describe ellipses," adds nothing to the major proposition, that "S., J., M., E., V., m., do so." It is merely the same proposition expressed in other words, so long as S., J., M., E., V., m., are supposed to be all the planets. And in the next place we have to make a remark which is more important; that the minor, in such an example, must generally be either a very precarious truth, or, as appears in this case, a transitory error. For that the planets known at any time are all the planets, must always be a doubtful assertion, liable to be overthrown to-night by an astronomical observation. And the assertion, as received in Kepler's time, has been overthrown. For Saturn, Jupiter, Mars, Earth, Venus, Mercury, are not all the planets. Not only have several new ones been discovered at intervals, as Uranus, Ceres, Juno, Pallas, Vesta, but we have new ones discovered every day; and any conclusion depending upon this premiss that A, B, C, D, E, F, G, H, to Z are all the planets, is likely to be falsified in a few years by the discovery of A´, B´, C´, &c. If, therefore, this were the syllogistic analysis of Induction, Kepler's discovery rested upon a false proposition; and even if the analysis were now made conformable to our present knowledge, that induction, analysed as above, would still involve a proposition which to-morrow may show to be false. But yet no one, I suppose, doubts that Kepler's discovery was really a discovery—the establishment of a scientific truth on solid grounds; or, that it is a scientific truth for us, notwithstanding that we are constantly discovering new planets. Therefore the syllogistic analysis of it now discussed (namely, that which introduces simple enumeration as a step) is not the right analysis, and does not represent the grounds of the Inductive Truth, that all the planets describe ellipses.
It may be said that all the planets discovered since Kepler's time conform to his law, and thus confirm his discovery. This we grant: but they only confirm the discovery, they do not make it; they are not its groundwork. It was a discovery before these new cases were known; it was an inductive truth without them. Still, an objector might urge, if any one of these new planets had contradicted the law, it would have overturned the discovery. But this is too boldly said. A discovery which is so precise, so complex (in the phenomena which it explains), so supported by innumerable observations extending through space and time, is not so easily overturned. If we find that Uranus, or that Encke's comet, deviates from Kepler's and Newton's laws, we do not infer that these laws must be false; we say that there must be some disturbing cause in these cases. We seek, and we find these disturbing causes: in the case of Uranus, a new planet; in the case of Encke's comet, a resisting medium. Even in this case therefore, though the number of particulars is limited, the Induction was not made by a simple enumeration of all the particulars. It was made from a few cases, and when the law was discerned to be true in these, it was extended to all; the conversion and assumed universality of the proposition that "these are planets," giving us the proposition which we need for the syllogistic exhibition of Induction, "all the planets are as these."
I venture to say further, that it is plain, that Aristotle did not regard Induction as the result of simple enumeration. This is plain, in the first place, from his example. Any proposition with regard to a special class of animals, cannot be proved by simple enumeration: for the number of particular cases, that is, of animal species in the class, is indefinite at any period of zoological discovery, and must be regarded as infinite. In the next place, Aristotle says (§ 10 of the above extract), "We must conceive that C consists of a collection of all the particular cases; for induction is applied to all the cases." We must conceive (νοεῖν) that C in the major, consists of all the cases, in order that the conclusion may be true of all the cases; but we cannot observe all the cases. But the evident proof that Aristotle does not contemplate in this chapter an Induction by simple enumeration, is the contrast in which he places Induction and Syllogism. For Induction by simple enumeration stands in no contrast to Syllogism. The Syllogism of such Induction is quite logical and conclusive. But Induction from a comparatively small number of particular cases to a general law, does stand in opposition to Syllogism. It gives us a truth,—a truth which, as Aristotle says (§ 14), is more luminous than a truth proved syllogistically, though Syllogism may be more natural and usual. It gives us (§ 11) immediate propositions, obtained directly from observation, and not by a chain of reasoning: "first truths," the principles from which syllogistic reasonings may be deduced. The Syllogism proves by means of a middle term (§ 13) that the extreme is true of a third thing: thus, (acholous being the middle term):
Acholous animals are long-lived:
All elephants are acholous animals:
Therefore all elephants are long-lived.
But Induction proves by means of a third thing (namely, particular cases) that the extreme is true of the mean; thus (acholous, still being the middle term)
Elephants are long-lived:
Elephants are acholous animals:
Therefore acholous animals are long-lived.
It may be objected, such reasoning as this is quite inconclusive: and the answer is, that this is precisely what we, and as I believe, Aristotle, are here pointing out. Induction is inconclusive as reasoning. It is not reasoning: it is another way of getting at truth. As we have seen, no reasoning can prove such an inductive truth as this, that all planets describe ellipses. It is known from observation, but it is not demonstrated. Nevertheless, no one doubts its universal truth, (except, as aforesaid, when disturbing causes intervene). And thence, Induction is, as Aristotle says, opposed to syllogistic reasoning, and yet is a means of discovering truth: not only so, but a means of discovering primary truths, immediately derived from observation.
I have elsewhere taught that all Induction involves a Conception of the mind applied to facts. It may be asked whether this applies in such a case as that given by Aristotle. And I reply, that Aristotle's instance is a very instructive example of what I mean. The Conception which is applied to the facts in order to make the induction possible is the want of the gall-bladder;—and Aristotle supplies us with a special term for this conception; acholous349. But, it may be said, that the animals observed, the elephant, horse, mule, &c., are acholous, is a mere fact of observation, not a Conception. I reply that it is a Selected Fact, a fact selected and compared in several cases, which is what we mean by a Conception. That there is needed for such selection and comparison a certain activity of the mind, is evident; but this also may become more clear by dwelling a little further on the subject. Suppose that Aristotle, having a desire to know what class of animals are long-lived, had dissected for that purpose many animals; elephants, horses, cows, sheep, goats, deer and the like. How many resemblances, how many differences, must he have observed in their anatomy! He was very likely long in fixing upon any one resemblance which was common to all the long-lived. Probably he tried several other characters, before he tried the presence and absence of the gall-bladder:—perhaps, trying such characters, he found them succeed for a few cases, and then fail in others, so that he had to reject them as useless for his purpose. All the while, the absence of the gall-bladder in the long-lived animals was a fact: but it was of no use to him, because he had not selected it and drawn it forth from the mass of other facts. He was looking for a mean term to connect his first extreme, long-lived, with his second, the special cases. He sought this middle term in the entrails of the many animals which he used as extremes: it was there, but he could not find it. The fact existed, but it was of no use for the purpose of Induction, because it did not become a special Conception in his mind. He considered the animals in various points of view, it may be, as ruminant, as horned, as hoofed, and the contrary; but not as acholous and the contrary. When he looked at animals in that point of view,—when he took up that character as the ground of distinction, he forthwith imagined that he found a separation of long-lived and short-lived animals. When that Fact became a Conception, he obtained an inductive truth, or, at any rate, an inductive proposition.



