Методика преподавания математики в начальной школе

б) табличное сложение и соответствующие случаи вычитания в пределах 10, в пределах 20 с переходом через десяток;

в) свойства действий сложения и вычитания: переместительное, сочетательное и правила вычитания числа из суммы и суммы из числа.

II. Методические приемы формирования устных вычислительных навыков сложения и вычитания

Работа над формированием вычислительными навыками (при выполнении всех вычислительных приемов устных и письменных) строится в соответствии с этапами:

I этап – подготовка к изучению вычислительного приема (изучение теоретической основы);

II этап – ознакомление с вычислительным приемом;

III этап – закрепление вычислительного умения, формирование вычислительного навыка.

При ознакомлении с каждым из вычислительных приёмов используются методические приёмы, способствующие их качественному усвоению. Долгие годы методическая копилка учителей пополнялась такими приемами. Эти приемы способствуют решению задачи – вооружить младших школьников устными вычислениями так, чтобы навык мог характеризоваться теми качествами, которые мы указали выше: правильностью, осознанностью, рациональностью, автоматизмом, прочностью.

Один из первых таких приемов, который применяется на первом же уроке ознакомления с любым из вычислительных приемов – это развернутая объяснительная запись. Ее мы видим почти во всех учебниках математики начальной школы (А.М.Моро – программа «Школа России», Л.Г.Петерсон – программа «Перспектива», В.Н.Рудницкая – «Школа 2100»):

43 + 4 = 49 + (1 + 3) = (49 + 1) + 3 = 50 + 3 = 53

48 – 3 = (40 + 8) – 3 = 40 + (8 – 3) = 40 + 5 = 45

Такая объяснительная запись показывает не просто все шаги тождественных преобразований в процессе выполнения каждой операции приема, но и раскрывает теоретическую основу приема. Ее мы рассмотрели выше в таблицах.

На последующих уроках, закрепляя вычислительные приёмы, необходимо сокращать объяснительную запись. Учителя в начальной школе используют для этого методические приёмы, раскрытые С.Н. Лысенковой:

1) «метод связывающих дуг»:

50

49 + 4 = 49 + (1 + 3) = 53,

90

73 + 20 = (70 + 3) + 20 = 93

2) «метод штриха»

48 – 3 = 45;

3. «метод усов»

45 + 8 = 40 + 13 = 53

40 5

Данные приёмы чаще всего применяются комбинированно:

49 + 4 = 53

49 + (1 + 3) = 50 + 3 = 53

При существующем многообразии методических приёмов для раскрытия приемов, выбор их зависит от специфики работы каждого учителя индивидуально, а так же от особенностей каждого класса в отдельности, но методика работы над каждым вычислительным приёмом содержит одни и те же этапы:

I этап – развернутая (пошаговая) запись вычислительно приёма на доске и в тетрадях

II этап – сокращение записи с помощью одного или нескольких методических приёмов;

III этап – краткая запись выражений с устными пояснениями для повышения качества формирования вычислительного навыка.

В процессе формирования вычислительных навыков осуществляется контроль его уровня.

Вместе с тем, учитывая, что ученик при выполнении вычислительного приёма, должен отдавать себе отчёт в правильности и целесообразности каждого выполненного действия, то есть постоянно контролировать себя, соотнося выполняемые операции с образцом – системой операций.

Арифметические действия

и методика их изучения в курсе математики начальной школы.

Формирование вычислительных навыков

у учащихся начальной школы

Устные приемы сложения и вычитания однозначных чисел с переходом через десяток в пределах 20.

Методика формирования вычислительного навыка младших школьников

После изучения приемов сложения и вычитания чисел в пределах десяти, на их основе учащиеся знакомятся с приемами сложения и вычитания однозначных чисел с переходом через разряд – через десяток в пределах 20 (концентр «Числа от 1 до 20»).

Представим в таблице эти приемы:

Виды

вычислительных приёмов

Необходимые знания

(теоретическая основа)

1. Сложение однозначных чисел с переходом через десяток:

6 + 8.

1) знание состава чисел в пределах десяти (таблица сложения однозначных чисел);

2) знание разрядного состава двузначных чисел.

2. Вычитание однозначных чисел с переходом через десяток:

12 – 7.

1) знание состава чисел в пределах десяти (таблица сложения однозначных чисел);

2) знание разрядного состава двузначных чисел.

3. Вычитание однозначных чисел с переходом через десяток:

12 – 7.

Знание состава двузначных чисел в пределах двадцати (таблица сложения однозначных чисел с переходом через десяток).

Прием сложения однозначных чисел состоит из 3 операций:

1) разложение второго слагаемого на сумму чисел, одно из которых может дополнить первое слагаемое до 10 (теоретическая основа – состав однозначных чисел, раскрытый в таблице сложения в пределах десятка);

6 + 8 =

4 4

2) прибавление к первому слагаемому, дополняя его до десяти (состав числа 10 – таблица сложения в пределах 10);

= (6 + 4) + 4 =

3) прибавление к полученному десятку оставшихся единиц от второго слагаемого (теоретическая основа – разрядный состав двузначных чисел).

= 10 + 4 = 14

Учащиеся рассуждают так: «8 – это 4 и 4. К 6 прибавим 4 до десяти. К десяти прибавим оставшиеся 4 единицы, получаем 14».

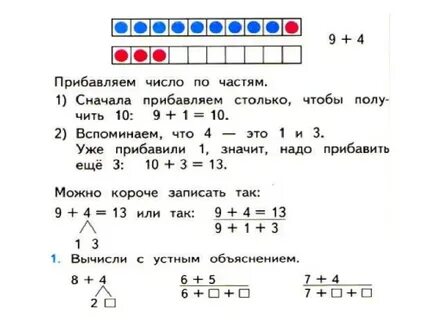
Данный прием четко показан в учебнике программы «Школа России» Математика. 1 класс. 2 часть.

Сложение рассматривается в последовательности прибавления чисел – 2, 3, 4, 5, 6, 7, 8, 9 с переходом через десяток. Эти случаи запоминаются учениками. А на уроке обобщения объединяются в таблицу, называемую «таблицей сложения однозначных чисел в пределах 20».

Вычитание демонстрируется с помощью двух способов.

I способ состоит из трех операций и выполняется по аналогии со сложением – по частям:

1) вычитаемое представляется в виде двух чисел, одно из которых равно разрядным единицам уменьшаемого (теоретическая основа – состав однозначных чисел, раскрытый в таблице сложения в пределах десятка);

12 – 7 = 12 – (2 + 5) =

2 5

2) из уменьшаемого вычитаем число равное единицам уменьшаемого до десятка (теоретическая основа – разрядный состав двузначных чисел);

= (12 – 2) – 5 =

3) из полученного десятка вычитаем оставшиеся единицы вычитаемого (состав числа 10 – таблица сложения в пределах 10).

= 10 – 5 = 5

Учащиеся рассуждают так: «Вычтем по частям. 7 – это 2 и 5. Из 12 вычтем 2 до 10. А теперь из 10 вычтем 5, получим 5».

II способ состоит из 2 операций:

1) уменьшаемое представляется в виде двух чисел, одно из которых равно вычитаемому (теоретическая основа – состав двузначных чисел, раскрытый в таблице сложения в пределах 20);

12 – 7 = (7 + 5) – 7 =

7 5

2) вычитание из суммы чисел слагаемого равного вычитаемому (теоретическая основа: особый случай вычитания – а – а =0).

(7 – 7) + 5 = 5

Учащиеся при этом рассуждают так: «12 – это 7 и 5. Значит, если из 12 вычесть 7, то получим 5». Так рассуждают дети.

– Найдите в учебнике Математика.1 класс. 2 часть урок, раскрывающий приемы вычитания.

– Чем изложенный материал на странице учебника отличается от представленного преподавателем?

Арифметические действия

и методика их изучения в курсе математики начальной школы.

Формирование вычислительных навыков

у учащихся начальной школы

Теоретико-множественный смысл произведения

План:

I. Теоретико-множественный смысл произведения целых неотрицательных чисел. Теоретико-множественный смысл равенств 0 × а = а и а × 0 = 0.

II. Теоретико-множественный смысл свойств умножения.

I. Теоретико-множественный смысл произведения целых неотрицательных чисел.

Теоретико-множественный смысл равенств а × 1= а и а × 0 = 0.

В школьном курсе математики используется определение умножения, которое связывается со сложением одинаковых слагаемых:

      Если а и b – целые неотрицательные числа, то произведением а × b называется число, удовлетворяющее следующим условиям:

1) а × b = а + а + . . . + а + а, при b > 1;

b раз

2) а × b = а, при b = 1;

3) а × b = 0, при b = 0.

Первое условие можно обосновать с теоретико-множественной точки зрения так.

Если множества А1, А2, …, Аb имеют по а элементов каждое, причем никакие два из них не пересекаются, то их объединение А1UА2U …U Аb содержит а × b элементов.

Таким образом, с теоретико-множественной позиции произведение

а × b, при b > 1, представляет собой число элементов в объединении b множеств, каждое из которых содержит по а элементов и никакие два из них не пересекаются:

а × b= n(А1 U А2 U …U Аb), если n(А1) = n(А2) = … = n(Аb)= а и А1, А2, …, Аb попарно не пересекаются.

Такой подход позволяет обосновывать выбор умножения при решении текстовых задач, связывая умножение натуральных чисел с операцией объединения.

Каждому ребенку дали по 3 конфеты. Сколько конфет у четырех детей?

Выясним выбор действия для ответа на вопрос этой задачи.

В задаче речь идет о четырех множествах, в каждом из которых три элемента. Требуется узнать число элементов в объединении этих четырех множеств. Если

n(А1) = n(А2) = n(А3)= n(А4)= 3, то n(А1 U А2 U А3 U А4) = n(А1) + n(А2) + n(А3) + n(А4)= 3 + 3 + 3 + 3= 3 × 4. Произведение 3 × 4 является математической моделью данной задачи. Т.к. 3 × 4 = 12, то получаем ответ на вопрос: у четырех детей 12 конфет.

Существует другое толкование умножения с теоретико-множественной позиции, которое связано с понятием декартова произведения множеств.

Этот подход следует из теоремы:

Пусть А и В конечные множества. Тогда их декартово произведение также является конечным множеством, причем выполняется равенство:

n(A × B) = n(A) · n(B).

Тогда A × B состоит из пар вида (a , b), (a , b), …, (a , b), число которых равно n.

Если n = 1, то n(A)= а, n(B) = 1, то в этом случае имеем: n(A × B) = n(A)· n(B) = а · 1 = а.

При k = 0 данное равенство также верно, поскольку B = Ø и n(A × Ø) = n(A)· n(Ø) = а · 0 = 0.

Из этого следует, что с теоретико-множественной с теоретико-множественной точки зрения произведение а · b целых неотрицательных чисел есть число элементов в декартовом произведении множества А и В, таких, что а = n (A), b = n (B):

а · b = n(A) · n(B) = n(A × B).

II. Теоретико-множественный смысл свойств умножения

Благодаря такому подходу и смысл свойств умножения как арифметического действия:

1) коммутативное свойство – а · b = b · a,

2) ассоциативное свойство – (а · b) · c = a · (b · c),

3) дистрибутивное свойство – (a + b) · c = a · c + b · c.

1) Смысл равенства а · b = b · a

Хотя множества A × B и В × А различны, они являются равномощными: каждой паре (а, b) из множества A × B можно поставить в соответствие единственную пару (b, a) из множества В × А, и наоборот. Значит, n(A × B) = n(В × A) и поэтому а · b = b · a.

а · b = n(A × B) = n(В × A) = b · a

2) Ассоциативность (а · b) · c = a · (b · c) доказывается аналогично.

Множества A × (B × С) и (A × B) × С различны, но равномощны: каждой паре (а, (b, с)) из множества A × (B × С) соответствует единственная пара ((а, b), с) из множества (A × B) × С и наоборот. Поэтому n(A × (B × С)) = n ((A × B) × С), а следовательно a (b c)= (а b) c.

3) Дистрибутивность умножения относительно сложения выводится из равенства * А ×(В U С) = (А × В) U (А × С), а вычитания из равенства А ×(В \ С) = (А × В) \ (А × С).

(Ұ а, b,c Є Z) a · (b + c)= a· b + a·c (a +b) · c= a· с + b ·c

а = n (A), b = n (B), с = n (С):

Если А умножить на В и С, то А ×(В U С) = (А × В) U (А × С)

a · (b · c) = n (A) × n(В U С) = n(A ×(В U С)) = n((А × В) U (А × С))=

на основе рав.*      

= n(А × В) + n(А × С) = a· b + a·c

Таким образом, умножение определяется через сложение, а особые случаи умножения с нулем принимаются по определению: а · 1 = а, а · 0 = 0.

Теоретико-множественный смысл частного

План:

I. Теоретико-множественный смысл частного целых неотрицательных чисел.

II. Теоретико-множественный смысл правил деления суммы на число и числа на сумму.

III. Теоретико-множественный смысл отношений «больше в», «меньше в».

IV. Теоретико-множественный смысл деления с остатком.

I. Теоретико-множественный смысл частного целых неотрицательных чисел

С теоретико-множественной      точки зрения деление чисел – операция обратная умножению и связывается с разбиением конечного множества на равночисленные попарно непересекающиеся подмножества и с его помощью решаются задачи двух видов:

– деление на равные части (нахождение числа элементов в каждом подмножестве разбиения);

– деление по содержанию (отыскание числа таких подмножеств).

Если а = n (A) и множество А разбито на попарно непересекающиеся равночисленные подмножества и если:

b – число подмножеств, то частное а : b – число элементов в каждом подмножестве;

b – число элементов в каждом подмножестве, то частное а : b – число таких подмножеств.

В соответствии с этим обосновывается выбор арифметического действия для решения задач:

а) Мама дала Пете 15 орехов. Он раздал поровну своим друзьям – Диме и Сереже, а также себе. Сколько орехов получил каждый мальчик?

В задаче рассматривается множество, в котором 15 элементов – орехов. Это множество разбивается на 3 равночисленных подмножества, т.к мальчиков трое. Требуется узнать число элементов в каждом таком подмножестве. Это число можно найти с помощью деления: 15 : 3. Вычислив значение этого выражения, получаем ответ на вопрос задачи: каждый мальчик получил по 5 орехов.

б) Доктор раздал 12 таблеток витаминов по 3 каждому ребенку. Сколько детей получили таблетки витаминов?

Множество из 12 элементов разбивается на подмножества, в каждом из которых по 3 элемента. Требуется узнать число таких подмножеств. Его можно найти с помощью деления: 12 : 3. Вычислив значение этого выражения – 12 : 3 = 4, получаем ответ на вопрос задачи: таблетки получили четыре ребенка.

II. Теоретико-множественный смысл правил деления суммы на число и числа на сумму

В математике при различных вычислениях пользуются правилами деления суммы на число. Дадим теоретико-множественное обоснование этим правилам.

Правило деления суммы на число:

Если частные а : с и b : с существуют, то (а + b) : с = а : с + b : с.

Пусть а = n (A), b = n (B) и A ∩ B= Ø. Если множества А и В можно разбить на равночисленные подмножества, состоящие из с элементов каждое, то и объединение этих множеств допускает такое же разбиение. Если при этом множество А состоит из а : с подмножеств, а множество В – из b : с подмножеств, то А U В состоит из а : с+ b : с подмножеств. Это и значит, что (а + b) : с = а : с+ b : с.

III. Теоретико-множественный смысл отношений «больше в», «меньше в»

С теоретико-множественной точки зрения рассматриваются и отношения «больше в», «меньше в», которые рассматриваются в текстовых задачах.

В аксиоматической теории определение этих отношений вытекает из определения натуральных чисел: если а : b = c, то можно говорить,

что «а больше b в с раз» или что «b меньше а в с раз». И чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее разделить на меньшее.

Если а = n (A), b = n (B) и известно, что «а меньше b в с раз», то поскольку а < b , то в множестве В можно выделить собственное подмножество, равномощное множеству А , но так как «а меньше b в с раз», то множество В можно разбить на с подмножеств, равночисленных множеству А.

Так как с – это число подмножеств в разбиении множества В, содержащего b элементов, а в каждом подмножестве – а элементов, то

с = b : а.

а) У Дениса было 3 тетрадей в клетку, а в линию в 4 раза больше. Сколько тетрадей было у Дениса?

В задаче речь идет о двух множествах: множестве тетрадей в клетку (А) и множестве тетрадей в линию (В). Известно, что n (A) = 3 и что в множестве В элементов в 4 раза больше, чем в множестве А. Требуется найти число элементов в множестве В, т.е. n (B).

Т.к. в множестве В элементов в 4 раза больше, чем в множестве А, то множество В можно разбить на 4 подмножества, равномощных множеству А. Поскольку в каждом подмножестве содержится по три элемента, то всего в множестве В будет содержатся четыре раза по 3 элемента: 3 + 3 + 3 + 3 или

3 × 4 элементов. Выполнив вычисления, получаем ответ на вопрос задачи: тетрадей в линию у Дениса 12.

А

В

б) У Дениса 10 солдатиков, а у Толи в 2 раза меньше. Сколько солдатиков у Толи?