Теоретико-мыслительный подход. Книга 1: От логики науки к теории мышления

Благодаря тому, что греки воспринимали природу в общем, именно им мы обязаны созданием наиболее общих понятий – категорий, отражающих всеобщую связь явлений природы, всеобщее движение и изменение. В числе этих категорий было понятие «бесконечного». Его появление и первый этап развития теснейшим образом связаны с возникновением и развитием понятия «первоначала».

§ 1. [Фалес и Анаксимандр][43]

Наблюдая движение и изменение всего существующего, люди, по-видимому, уже очень давно пришли к необходимости как-то обозначить тот факт, что, несмотря на все изменения и переходы одного в другое, в этом преходящем и изменяющемся всегда остается нечто, что действует на человека и вызывает в нем ощущения. Греческие натурфилософы называли обычно это нечто «первоначалом». Действительный смысл этой абстракции заключается в том, что она выделяла одно свойство объективного мира, сам факт его существования и действования на человека, отрицая все другие свойства. Однако греческие философы не только не осознавали четко того, какие свойства отражены в этой абстракции, но и того, что это абстракция, то есть название отдельного свойства[44]. Это противоречие, как мы показали в первой главе, присуще всякой абстракции. Но здесь оно усугубилось тем, что абстракция первоначала отрицает все чувственные свойства предметов, всякую чувственную определенность, то есть, по существу, отрицает чувственность вообще. Стремясь наделить абстракцию первоначала реальным чувственным существованием, втиснуть в нее различные воспринимаемые чувствами свойства и предметы, ранние греческие философы постоянно впадали в противоречия. Но эти противоречия были исключительно плодотворными, так как они заставляли мышление двигаться вперед и в этом движении рождались абстрактные понятия «всеобщего», «бытия», «сущего», «бесконечного» и др. (освобожденные от чувственных представлений).

Первым (из известных нам) греческим философом, выделившим абстракцию первоначала, был Фалес[45]. Эта абстракция должна была по своему значению отказаться от всякой чувственной определенности. Она утверждала, что, несмотря на чувственные различия, вопреки им, во всех предметах есть что-то общее. От чувственной определенности сознание должно было перейти к абстракции, настолько общей, что она не имела чувственного содержания. Этот переход к абстрактному внечувственному всеобщему был настолько труден, что Фалес наделил это всеобщее особенной чувственной формой. Он считал первоначалом воду. Таким образом, выделив всеобщее, Фалес придал ему форму наглядного особенного предмета, заложив как в названии этого предмета, так и в абстракции всеобщее противоречие. Его вода, во-первых, обозначала определенное чувственное существование, во-вторых, существование вообще. И хотя Фалес уже различал эти два момента, он не мог разделить их, так и не мог создать абстракцию существования, оторвавшись от наглядных образов того или иного определенного существования.

Анаксимандр, по-видимому, уловил это противоречие и пытался его разрешить. Поэтому он назвал первоначало «апейрон» (τὸ ἄπειρον), то есть неопределенным или безграничным. Ход его мысли кажется нам достаточно ясным. Всеобщее, остающееся при всех изменениях неизмененным, пребывающее, то, из чего все возникает, и то, во что исчезает, как в последнее, не может быть ни водой, ни воздухом, не землей, ни огнем, ни вообще чем-либо определенным, ибо все определенное преходяще. Первоначало не может быть определенным и оформленным, оно неопределенно и бесформенно. Отсюда уже недалеко утверждение, что первоначало безгранично или бесконечно, ибо граница есть форма качественной определенности. Обозначение первоначала как неопределенного и безграничного было большим шагом вперед в сознании содержания этого понятия, однако, дав первоначалу эти названия, Анаксимандр сам еще не полностью освободился от иллюзий, связанных с чувственными представлениями. Он пытался наделить «бесконечное» актуальным, природным существованием.

Анаксимандр пытался также подкрепить свое обозначение первоначала как безграничного и бесконечного обращением к процессам возникновения и изменения, происходящим в объективном мире. «В качестве основания для определения первоначала как бесконечного он указывает на то, что непрекращающемуся порождению никогда не должно недоставать материала» [Гегель, 1932, IX, с. 166].

Само обращение к процессам развития и изменения для обоснования абстракции бесконечного очень важно, но форма, в какой это сделал Анаксимандр, неудачна, ибо он хотел применить «бесконечное» не к самому реальному процессу развития и изменения, а к фиктивному и в его представлении неподвижному первоначалу, из которого все возникает. Поэтому в последующем Аристотель, в общем, правильно разрешивший вопрос о содержании абстракции бесконечного, отводит его соображение. «Ведь для того, чтобы не прекратилось возникновение, нет необходимости чувственно-воспринимаемому телу быть актуально бесконечным, так как [вполне] допустимо, что гибель одного будет возникновением для другого и при конечности целого» [Физика, 208а8—12].

Таким образом, абстракция первоначала, всеобщего появляется как отражение одной из сторон движения и изменения объективного мира. Сначала это всеобщее пытаются представить в форме чувственного и особенного, но это приводит к противоречиям, и тогда появляется абстракция неопределенного (бесконечного). Пока эта абстракция является чисто отрицательной. Сама по себе она еще не имеет никакого смысла, никакого содержания. Она только отрицает всякую чувственную определенность, выражает лишенность. Она находится еще в худшем положении, чем остальные абстракции, которым соответствуют хоть какие-то чувственные образы. Абстракция неопределенного, бесконечного отрицает чувственное и благодаря этому теряет все свое содержание. Но в противопоставлении последовательно всех чувственных определенностей их отрицанию рождается абстрактное понятие. Сама эта форма противопоставления является первой простейшей формой понятия.

Противопоставление абстракций определенного и неопределенного выражает мысленный анализ явлений действительности. Каждая из его частей не имеет пока смысла вне этого противопоставления, вне анализа, хотя абстракция «определенного», «конечного», «ограниченного» имеет определенное содержание в чувственных наглядных образах воды, земли, воздуха, огня и вообще в совокупности всех чувственных предметов и в каждом из них. Но мы говорим здесь об абстрактном логическом содержании, а оно имеется лишь в форме противопоставления этих двух абстракций, и, наоборот, противопоставление этих двух абстракций получает определенное содержание и является понятием.

Но в этой форме выражается совсем не то содержание, которое хотел выразить Анаксимандр. Действительное содержание понятия первоначала не может быть выражено только в форме противопоставления неопределенного определенному, ведь первоначало содержится и в воде, и в воздухе, и в земле, и в огне, то есть во всем определенном. Поэтому вслед за первым суждением возникает второе, противоречащее ему.

Противоречие между этими двумя суждениями выражает все то же, уже известное нам противоречие, присущее любой абстракции. «Неопределенное», «бесконечное» должно служить обозначением отдельного свойства «существования», отрицающего всякую чувственную определенность. Но, с другой стороны, всякое существование носит чувственный характер, проявляется в существовании определенных чувственных предметов. Противоречие между абстрактным (логическим) знанием и чувственным находит себе выражение в противоречии этих двух суждений, и разрешение его возможно только за счет отказа от чувственного знания и осознания его в логической, абстрактной форме.

§ 2. [Пифагорейцы и Анаксимен]

Дальнейшее развитие понятия «первоначало» и «бесконечное» получили в философии пифагорейцев. Их заслуга заключается в том, что они ввели в философию и систематически исследовали количественные отношения[46] и числа, но в то же время благодаря этому вся их философия приобрела мистический числовой характер.

Основное положение пифагоровской философии гласит, «что элементы чисел суть элементы всего существующего и что все небо есть гармония и число» [Метафизика, 986а2—3][47].

Здесь шаг вперед заключается в том, что первоначало природы было выражено как нечто нечувственное, бестелесное[48].

Однако этот отрыв от чувственных представлений не мог быть полным из-за своей обратной стороны – [проблемы] превращения числа в субстанцию, [проблемы] его объективирования. Отсюда сразу же возникал целый ряд противоречий. Абстракция первоначала может быть понята только как абстракция всеобщего, как абстракция существования. Здесь же в основание абстракции положено не всеобщее свойство существования, а особенное, частное свойство вещей – величина и мера. Как бы ни определяли числа пифагорейцы, каким бы абстрактным содержанием они их ни наделяли, в сознании каждого человека числа выступают как особенная количественная характеристика, и попытка положить их в основание всех свойств объективного мира вызывает возражения. Так Аристотель справедливо говорит: «они [пифагорейцы] ничего не говорят о том, откуда возникает движение, если (как они считают) в основе лежат только предел и беспредельное, нечетное и четное, и каким образом возникновение и уничтожение или действия несущихся по небу тел возможны без движения и изменения», и дальше: «если согласиться с ними, что из этих начал образуется величина ‹…›, то все же каким образом получается, что одни тела легкие, а другие тяжелые?» [Метафизика, 990а8—13].

Кроме того, возникают возражения со стороны чувственности: «Где находятся числа? ‹…› Они не суть непосредственно сами вещи, ибо вещь, субстанция, отнюдь не является числом; тело не имеет с ним никакого сходства» [Гегель, 1932, IX, с. 195].

Пифагорейцы сделали также большой шаг вперед в основании абстрактной формы понятий. «Существуют три разных способа мыслить вещи: во-первых, со стороны различия; во-вторых, со стороны противоположности; в-третьих, со стороны отношения. То, что рассматривается со стороны одного лишь различия, рассматривается само по себе; это – субъекты, каждый из которых соотносится только с самим собой, например лошадь, растение, земля, воздух, вода, огонь. Они мыслятся отрешенно, не в отношении к другому. ‹…› Со стороны противоположности одно определяется нами как всецело противоположное другому, например добро и зло, справедливое и несправедливое, святое и несвятое, покой и движение и т. д. Со стороны отношения мыслится предмет, определяемый по своему безразличному отношению к другому, как, например, лежащее направо и лежащее налево, верхнее и нижнее, двойное и половинное» (Секст Эмпирик) (цит. по [Гегель, 1932, IX, с. 192])[49].

Эти успехи в понимании отношений между абстракциями позволили пифагорейцам сделать шаг вперед в осознании действительного содержания абстракции бесконечного. В соответствии со своей классификацией они отнесли бесконечное к противоположностям, то есть к тем «вещам», которые определяются «как всецело противоположные другому». Противоположностью бесконечному (безграничному) в пифагорейской таблице противоположностей[50] была граница.

В общем, движение вперед в развитии понятия бесконечного у пифагорейцев заключалось в том, что они четко определили бесконечное как противоположность границе и сделали его лишь частным определением первоначала, наряду с единым и ограниченным.

Одновременно, исследуя количественные отношения и числовые ряды, пифагорейцы подходили к совершенно иному пониманию бесконечного, но мы остановимся на этом специально в дальнейшем.

Итак, мы сказали, что выдвинутое пифагорейцами понимание первоначала как числа приводило к ряду противоречий. Эти противоречия отчасти были разрешены в философии Анаксимена.

По-видимому, в противоположность пифагорейской философии, Анаксимен опять взял в качестве первоначала определенное – воздух. Он, должно быть, находил, что первоначало необходимо должно быть чувственным, а воздух имеет то преимущество, что обладает большей бесформенностью. В то же время Анаксимен учел результаты пифагорейской философии и ввел в свое первоначало бесконечность как количественную неопределенность[51].

Таким образом, в философии Анаксимена абстракция первоначала как бы завершает круг своего развития и приходит, казалось бы, к тому же, с чего мы начали: к определенной неопределенности. Но в процессе движения этой абстракции отделились друг от друга две ее характеристики – качество и количество. Анаксимен сочетает качественную определенность первоначала с ее количественной бесконечностью. Это создает противоречие, так как всякая качественная определенность всегда ограничена, в противном случае, то есть если бы рядом с ней не было другого, она не была бы качественной определенностью. Разрешение этого противоречия возможно только за счет образования новой абстракции, выражающей неопределенность качества, и эта абстракция вводится философией элеатской школы.

В то же время с переносом «бесконечного» в область количества начинается новый этап в развитии этой абстракции, этап, в котором она впервые получает положительное содержание и превращается в понятие, но это уже тема дальнейшего изложения.

Таким образом, мы видели, что до сих пор развитие понятия «бесконечное» было неразрывно связано с развитием понятия «первоначало». Сначала «бесконечное» выступает как всеобщее, как отрицание всякой чувственной определенности, в том числе и границы, но ее содержание не осознается. Оно составляет простейшее понятие, вместе с противоположной ему абстракцией «конечного», «ограниченного». Пифагорейцы осознают это противопоставление, и в то же время оно приобретает у них количественный характер. Анаксимен сочетает качественную определенность с количественной неопределенностью, бесконечностью.

Все это движение абстракции происходит на чувственной основе, хотя ее смысл и назначение заключается именно в отрицании чувственности.

§ 3. [Зенон, Анаксагор и Демокрит]

Мы уже сказали, что пифагорейцы и Анаксимен, переводя бесконечное в область количества, подходили к совершенно новому определению понятия бесконечного, связанного с процессами измерения, счета и деления величин.

Развивающееся искусство счета с необходимостью приводит, в конце концов, к понятию о бесконечно большом множестве. Каково бы ни было число сосчитанных предметов, можно прибавить еще один предмет, и счет приведет к большему числу; количество чисел может таким образом увеличиваться неограниченно, превосходя любое заданное число.

Данный предмет, данную линейку можно разделить на любое число равных частей, каждую часть можно подвергнуть новому делению, неограниченно его продолжая. Это приводит к частям, число которых может быть сделано больше любого заданного числа, и сами части становятся сколь угодно малыми.

Бесконечно большие и бесконечно малые появляются в процессе измерения. Чтобы найти отношения, скажем, двух отрезков, нужно отыскать их общую меру, то есть отрезок, содержащийся в каждом из них целое число раз; а для этого нужно меньший отрезок отложить на большем столько раз, сколько уложится; если получится остаток, то его нужно откладывать на меньшем отрезке, второй же остаток на первом и т. д.; остаток, который отложится в предыдущем целое число раз и представляет собой общую меру наших отрезков. Этот прием, известный под названием последовательного деления, был известен уже в глубокой древности, причем уже пифагорейцы знали, что он не всегда приводит к цели, то есть возможны случаи, когда последовательное деление никогда не даст остатка, откладывающегося целое число раз в предыдущем; такой случай имеет, например, место, когда мы ищем отношение диагонали квадрата к его стороне. В таком случае число последовательных делений становится бесконечно большим, а последовательные остатки – бесконечно малыми.

Исходя из имеющихся материалов, мы не можем с полной определенностью решить вопрос о том, связывали ли пифагорейцы абстракцию бесконечного с этими процессами. Возможно, что не связывали, так как в их таблице противоположностей «бесконечное» противостоит «границе», а «единому» противостоит «множество».

Анаксимен ввел абстракцию «бесконечного количества». Сама абстракция «количества» возникает из процессов сравнения и измерения, а «бесконечное количество» означает, что этот процесс нельзя довести до конца. Но у нас совершенно нет основания утверждать, что Анаксимен понимал действительное значение введенной им абстракции, и даже более того, мы не можем утверждать, что он сталкивался когда-либо с невозможностью довести процесс измерения или деления до конца и связывал с этими случаями абстракцию бесконечного. Вероятнее всего, что введенная им абстракция выражала все тот же известный всем философам факт, что у первоначала не может быть границы.

Связь абстракции бесконечного с процессами измерения, последовательного деления и счета явственно выступает впервые у Зенона, философа элеатской школы. В своей апории «дихотомия» он показал процесс деления, который никогда не может быть доведен до конца. Сущность его рассуждения заключается в следующем. Пусть необходимо пройти отрезок АВ=а. Но очевидно, что, прежде чем пройти АВ, надо пройти половину его АВ1=a/2. Но прежде чем пройти АВ1, надо пройти половину его АВ2=а/4 и т. д., и т. д.:

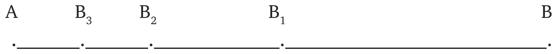
Рис. 1

Таким образом, получается бесконечное количество отрезков, которое надо было пройти за конечный промежуток времени, а это казалось Зенону невозможным. Нам здесь важен тот момент, что процессы повторного деления привели Зенона к необходимости ввести если не формально, то, во всяком случае, по существу абстракции «бесконечно большого» количества и «бесконечно малой» величины. «Зенон доказывает, что если существует множественное, то оно и велико и мало; оно настолько велико, что множественное бесконечно по своему количеству. ‹…› Оно так мало, что не имеет величины» (Симплиций)[52]. Но в этих абстракциях, в самом их названии уже заложены противоречия. Что может означать, например, абстракция «бесконечно малая величина»? Абстракция величины предполагает определенные границы, «бесконечное» эти границы отрицает. Что же остается? Величина, не имеющая никакой величины. Зенон прекрасно осознает, что это противоречие, и исходя из него отрицает возможность существования как бесконечно больших, так и бесконечно малых: «Он показывает, что того, что не имеет ни величины, ни толщины, ни массы, не существует. Ибо если бы мы его прибавили к другому, оно не увеличило бы последнего; если именно оно не имеет величины и прибавляется к другому, оно ничего не может присовокупить к величине этого другого и, таким образом, то, что прибавляется, есть ничто. Точно так же, если его отнимут от другого, последнее вследствие этого не уменьшится; оно, следовательно, есть ничто» [Гегель, 1932, IX, с. 233–234].

Таким образом, абстракции «бесконечно большого» и «бесконечно малого» не только содержат в себе обычное противоречие между чувственной и абстрактно-логической формой знания, но в последнем [случае] в них содержится противоречие, вызванное углублением человеческого знания. С помощью процесса деления Зенон, по существу, уже перешел от постоянных величин к переменным. Изменилось содержание, с которым он соотносит абстракции величины и количества, а форма этих абстракций осталась прежней.

Противоречие, заложенное в абстракции бесконечно малой величины, развили дальше Анаксагор и Демокрит.

Основу вещей, согласно Анаксагору, составляет бесчисленное множество качественно-определенных материальных частиц, которые Аристотель впоследствии назвал «гомеомериями». Эти гомеомерии, по Анаксагору, не могут иметь определенные величины, ибо все вещи делимы до бесконечности, и сколько бы их ни делили, они не перестают существовать. Уменьшается только их величина. «И в малом ведь нет наименьшего, но всегда есть меньшее. Ибо бытие не может разрешаться в небытие» (Симплиций. Комментарии на «Физику» Аристотеля, 164, 16)[53]. Таким образом, Анаксагор берет одну сторону противоречия, возможность делить любую величину без конца, и оставляет в стороне вопрос о том, что же останется в результате этого деления.

Демокрит решает вопрос иначе. Ему кажется невероятным, чтобы деление тел можно было продолжать каждый раз снова и снова, ведь так в результате ничего не останется. Поэтому он считает, что в процессе деления мы, в конце концов, приходим к частицам, хотя и обладающим определенной величиной[54], но дальше уже неделимым (атом). Таким образом, Демокрит взял другую сторону противоречия – невозможность актуального существования бесконечно делимых величин – и оставил в стороне вопрос о том, могут ли существовать величины дальше неделимые.

Мы уже видели, что абстракции «бесконечно малой величины» и «бесконечно большого количества» возникают в связи с процессами деления. По существу, они должны выражать свойства самого процесса. Но так как люди привыкли судить о процессе по его результатам, скажем, по тому последовательному ряду отрезков, который получается в результате деления линии, то свойства самого процесса переносятся ими на его результаты. В этом и состоит ошибка Анаксагора.

В конспекте лекций Гегеля по истории философии В. И. Ленин писал по поводу апорий Зенона: «Движение есть сущность времени и пространства. Два основных понятия выражают эту сущность: (бесконечная) непрерывность (Kontinuital) и “пунктуальность” (=отрицание непрерывности, прерывность). Движение есть единство непрерывности (времени и пространства) и прерывности (времени и пространства). Движение есть противоречие, есть единство противоречий». «Сущность времени и пространства есть движение…; понять его значит высказать его сущность в форме понятия. Движение как понятие, как мысль высказывается в виде единства отрицательности и непрерывности; но ни непрерывность, ни точечность сами по себе нельзя полагать в качестве их сущности», – приводит В. И. Ленин высказывание Гегеля и замечает: «верно!» [Ленин, 1969б, с. 231].

Эти положения справедливы для любых процессов, связанных с пространством и временем. Анаксагор полагает непрерывность пространства в качестве самостоятельной сущности.

Частичное разрешение противоречия, заключенного в абстракциях «бесконечно малого» и «бесконечно большого», было возможно за счет перехода от результатов процессов деления и счета к самим процессам, и это было сделано Аристотелем.

§ 4. [Аристотель]

Абстракция «бесконечного» образуется, как мы видели, в противоположность «конечному», как отрицание границы, конца, и поэтому на первом этапе своего развития связана с чувственным созерцанием, с данными опыта лишь отрицательно. Несмотря на это, оперируя абстракцией бесконечного, античные философы постоянно обращаются к непосредственному чувственному опыту, к наглядности. Естественно, что такое обращение с «бесконечным» приводит к противоречиям. Иногда это проявляется в том, что хотят представить себе бесконечное непосредственно, как тело или субстанцию. Чаще же выражают отвлеченное содержание этой абстракции в суждении, в другом суждении – чувственное содержание опыта и затем выявляют противоречие между этими суждениями.

Особенно много внимания уделяли этим противоречиям философы элеатской школы и тем весьма способствовали выяснению отношения между чувственностью и мышлением. В их рассуждениях абстракции и понятия освобождались от чувственного содержания и получали свою абстрактно-логическую форму.

Рассуждения, которыми пользовались элеаты, чтобы выявить противоречия, довольно просты. Например, основатель школы Ксенофан рассуждал так[55]:

«Первоначало есть всеобщее.

Пусть первоначало ограничено.

Ограниченное есть то, рядом с которым лежит другое.

Но то, что рядом с собой имеет другое, не есть всеобщее.

Значит, первоначало не ограничено».

Но тут же он доказывал, что первоначало не может быть неограниченным.

«Первоначало есть сущее (то есть существующее).

Все сущее имеет границы (начало, конец и т. п.).

Значит, первоначало ограничено».

Точно так же рассуждал Зенон, когда хотел доказать, вопреки показаниям чувств, что все едино[56]:

«Пусть все множественно. (Это значит, что какую бы частицу сущего мы ни взяли, она всегда будет множественной.)»