Космос. Иллюстрированная история астрономии и космологии

Вплоть до эпохи Коперника это движение рассматривалось как «движение восьмой сферы» – сферы, которая, как полагали, несет на себе звезды. Как мы сказали бы сегодня, исходя из коперниканской концепции, это была подвижная система отсчета. Земная ось совершает медленное конусообразное движение, приводящее к кажущемуся круговому движению точек равноденствия по эклиптике с востока на запад. Известно, что это «предварение равноденствий», или прецессия, составляет чуть более 50″ в год или 1° за 72 года. Гиппарх пришел к выводу, что эта величина должна быть не меньше, чем один градус за сто лет – по-настоящему выдающееся открытие. Но неужели оно было сделано исключительно из сопоставления звездных положений?

Движение точек равноденствия, очевидно, влияет на соотношение, связывающее продолжительность года, измеряемого по возвращению Солнца к какой-либо выбранной звезде, и по его возвращению в одну из равноденственных точек (или точек солнцестояния). В предыдущей главе мы показали, что последний период, называемый тропическим годом, короче первого – сидерического года. Гиппарх знал величину этой разности, и хотя он действительно пытался определить это медленное движение путем рассмотрения положений звезд, указанных Тимохарисом, скорее всего, более точный результат был получен им из сравнения сидерического и тропического годов. Его данные для последнего периода охватывают наблюдения равноденствий со 162 по 128 г. до н. э. и наблюдения лунных затмений, ценность которых заключается в том, что они позволяют точно определить положения, когда Луна, Земля и Солнце находятся на одной линии. Он довольно точно установил продолжительность тропического года, оказавшегося у него равным 365¼ суток минус 1/300 часть суток. На самом деле, последняя дробь должна равняться примерно 1/128, но Птолемей признавал первое соотношение правильным. Нам не известно значение, полученное Гиппархом для сидерического года, и мы можем дать только приблизительную оценку этой величины, основываясь на верхней границе интервала, приведенного им для прецессионного движения. (Если исходить из 1° за сто лет, то она оказывается равной 365¼ суток, плюс 1/144 часть суток.)

Иногда бывает полезно поразмышлять о том, насколько мало мы знаем о последовательности предпринятых действий, а значит и о мотивах проведения столь колоссальной астрономической работы. Что подсказало Гиппарху правильный путь определения того явления, которое мы сегодня называем прецессией, – продолжительность ли года, или положения звезд, или счет ночного времени? Точные положения звезд были нужны Тимохарису, возможно, только для определения продолжительности лунного месяца. Его наблюдения Луны не предполагали проведение угловых измерений: они сводились к наблюдению покрытий звезд с отсчетом времени в сезонных часах.

Сегодня было бы абсурдно, подражая пан-вавилонистам, говорить о ближневосточном «открытии прецессии». Как показано в первой главе, в каком-то смысле «понимание прецессии» не было чуждо и доисторическим наблюдателям, обнаружившим, что восходы и заходы звезд происходят не в местах, отмеченных их предками. В известном отношении, об этом движении знали и вавилонские астрономы, первыми осознавшие существование различия между тропическим и сидерическим способами измерения долготы Солнца. Однако, даже если мы сделаем такое заявление, это не означает, будто кто-либо из древних наблюдателей был способен предложить рациональное обоснование указанного расхождения, как это сделал Гиппарх. Решающим фактором в данном случае является достижение Гиппархом правильного понимания универсальности этого едва заметного смещения звезд после довольно продолжительного периода, когда он полагал, что оно относится исключительно к звездам зодиакального пояса.

ГИППАРХ О СОЛНЦЕ, ЛУНЕ И ПЛАНЕТАХ

Гиппарх успешно использовал два геометрических приема, уже применяемых ранее Аполлонием, – эксцентрик и эпицикл. В принципе, первого приема вполне достаточно, чтобы довольно точно рассчитать движение Солнца, и Гиппарх, использовав данные по продолжительности сезонов, получил все необходимые параметры, удовлетворявшие доступным ему наблюдениям. Он пришел к заключению, что эксцентриситет составляет 1/24 радиуса эксцентрического круга, а направление апогея (точки, находящейся на самом большом расстоянии от Земли) совпадает с 5½° Близнецов. Последнее значение весьма близко к истине, но первое – сильно завышено. (Округленное значение для эксцентриситета составляет около 1/60.) Однако примечательным здесь является не точность вычислений Гиппарха, а его умение применить наблюдательные данные, записанные в вавилонской стилистике, к греческим моделям. Он попытался сделать то же самое для движения Луны, но здесь он столкнулся с гораздо более серьезными проблемами, несмотря на то что у него была возможность черпать информацию из вавилонских источников с очень точными значениями основных компонентов, составляющих движение Луны, – четырех типов месяцев (синодического, сидерического, драконического и аномалистического).

Гиппарх проявлял особое усердие в поиске периодов наступления затмений, главным образом исходя из чисто исследовательского интереса, но также и потому, что они могли помочь точнее определить положения – а значит, и движения – Солнца и Луны. Ему удалось сравнить собственные данные по затмениям с вавилонскими; а тремя столетиями позже то же самое сделал Птолемей. Ни один другой греческий астроном, живший до Гиппарха, не обращался к этому материалу, но, повторим это еще раз, гораздо важнее было то, для чего он его использовал и к чему применил. Он разработал простейшую эпициклическую лунную модель, замечательную тем, что ее расчетные движения находились в полном соответствии с наблюденными движениями Луны. Он определил движение эпицикла вокруг Земли в соответствии с известным средним движением Луны по эклиптической долготе, а движение Луны в эпицикле синхронизировал с наблюденным «движением Луны в аномалии». (Аномалистический месяц – это период возвращения Луны к исходной скорости, фактически совпадающий со временем обращения от перигея до перигея.) Он нашел геометрическую процедуру, которая позволила ему вывести относительные размеры кругов и движения по ним, основываясь на времени трех лунных затмений. Он применил свой метод к двум различным тройкам затмений, используя в первом случае описанную нами выше эпициклическую, а во втором – эквивалентную ей эксцентрическую модели. (Об их эквивалентности см. предыдущий раздел, фрагмент об Аполлонии.)

Его расчеты оказались небезупречными, но сам метод был превосходен и в высшей степени оригинален. Спустя три столетия Птолемей еще более усовершенствовал его. Модель Гиппарха позволяла осуществлять весьма удовлетворительные расчеты положений Луны в сизигиях, то есть в новолуние и полнолуние. По словам Птолемея, Гиппарх, по-видимому, сам осознавал, что для промежуточных положений она не столь хороша, но, похоже, не прилагал усилий улучшить ее.

Гиппарх не ограничился моделью предвычислений только лунных долгот. Аналогичным образом, использовав собственные и вавилонские данные, он установил, что максимальная широта Луны, при отсчете от эклиптики, составляет 5°. У него было ясное понимание трехмерности относительных положений Солнца, Луны и Земли во время затмений, и он разработал геометрические процедуры для расчета действительных расстояний Солнца и Луны от Земли, которые могли быть успешно высчитаны из доступных ему наблюдений. Полученные им результаты содержали серьезные ошибки, но главным образом из‐за некритичного отношения к полученным им верхним и нижним границам их значений. Так, среднее расстояние до Луны было установлено им в интервале между 59 и 67⅓ земного радиуса. Ни один из предыдущих астрономов не подошел столь близко к правильному решению – чуть более 60 земных радиусов. Для расстояния до Солнца он привел величину, оказавшуюся меньше пятидесятой доли истинного значения, но он, по крайней мере, понял свою беспомощность в решении этого вопроса: он не смог измерить параллакс Солнца, но выдвинул оценочное численное предположение. Он исходил из семи минут дуги, хотя, на деле, это значение близко к девяти секундам. (На ил. 56 приведена геометрическая модель, на которой он основывал свои вычисления.)

В общем случае «параллаксом» называют угол изменения видимого положения объекта при рассматривании его из двух различных пунктов (см. ил. 57). Забегая вперед, отметим, что, поскольку Земля движется по своей орбите вокруг Солнца, угол отклонения какой-либо близко расположенной звезды будет меняться и она будет постепенно описывать на небе крошечный эллипс на фоне удаленных звезд (см. левую часть рисунка). За один год она опишет один полный эллипс. Астрономы не имели возможности зарегистрировать его до XIX в. Этот звездный параллакс (или «годичный параллакс») необходимо отличать от суточного параллакса, столь важного для внесения поправок в предвычисленные солнечные и лунные положения. Они, будучи рассчитанными на основе планетных моделей, соотносятся с центром Земли. Однако наши наблюдения Солнца и Луны осуществляются из точки, отстоящей от центра Земли более чем на 6350 километров. Если мы наблюдаем какой-либо объект, когда он находится точно над нашей головой, то параллакс, очевидно, должен равняться нулю, поскольку мы сами (в точке D на правой части рисунка), центр Земли и наблюдаемый объект – все это располагается на одной линии. Очевидно, что угол параллакса возрастает до максимума, когда объект находится вблизи горизонта, а мы – в точке B на упомянутом рисунке. Когда мы говорим о солнечном или лунном параллаксе в широком смысле, мы имеем в виду эти максимальные значения. Они, очевидно, напрямую связаны с расстояниями до рассматриваемых тел и с радиусом Земли, и начиная с XVIII в. их точные значения было принято приводить в расчете относительно экваториального радиуса. Именно это легло в основу устойчиво сложившегося терминологического оборота «средний экваториальный горизонтальный параллакс» – сложное выражение, характеризующее простую величину.

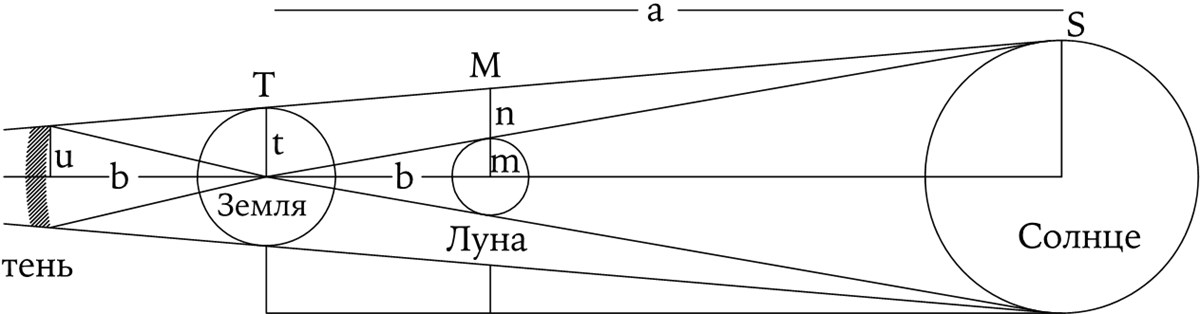
56

Пытаясь определить расстояния до Солнца (a) и Луны (b) в радиусах Земли (t), Гиппарх следовал примеру Аристарха (ил. 50). Он достаточно точно определил значения их видимых угловых размеров (полагая их равенство друг другу). Он считал, что угловые размеры земной тени на лунном расстоянии в 2½ раза превосходят размеры Луны. Однако этого было недостаточно: по его оценкам, солнечный параллакс должен быть равен 7 минутам дуги, что эквивалентно расстоянию в 490 земных радиусов. (О понятии параллакса см. с. 157.) Версия его собственного доказательства утрачена, однако ее можно восстановить по описаниям, оставленным Птолемеем. Как и у Аристарха, она, по-видимому, была избыточно геометричной и рассудочной, но Гиппарх, очевидно, обладал бо́льшим опытом в использовании приближений, точнее согласующихся с малыми углами в численном отношении. Они приведены здесь без дополнительных пояснений. Расстояние, обозначенное на рисунке буквой n, не играет большой роли и будет впоследствии исключено. Поскольку Земля находится между Луной и собственной тенью, ее радиус t определится как среднее арифметическое значений u и (n + m). Отрезки, обозначенные как n и t, являются основаниями подобных треугольников, а значение (n ÷ t) равно отношению (SM/ST). Последнее отношение, в свою очередь, равно (a – b) ÷ a, поскольку отрезки, обозначенные этими буквами, также являются соответствующими сторонами подобных треугольников. (Для большей очевидности и во избежание путаницы эти треугольники изображены в нижней части рисунка.) Теперь в нашем распоряжении есть все необходимое – два уравнения, из которых можно исключить n:

2t = m + n+ u и n ÷ t = (a – b) ÷ a.

Гиппарх полагал, что на среднем расстоянии от Земли угол, противолежащий радиусу Луны (то есть отрезку длиной m), составляет 1/1300 часть ее орбиты (которая равна 2pb). Из всего этого, а также из оценочных значений, полученных им для u и a (они приведены выше), можно найти, что расстояние до Луны равно примерно 67,2 радиуса Земли (Гиппарх получил значение 67⅓). Гораздо большего внимания заслуживает проведенная в работе оценка погрешностей. Что бы произошло, если бы Солнце находилось на еще большем расстоянии от Земли? Если бы оно было удалено на бесконечное расстояние, то величина, обратная 490 в последнем вычислении, обратилась бы в ноль, что определило бы минимальное расстояние до Луны как величину, чуть бо́льшую 59 земных радиусов. По современным данным, среднее значение этой величины – 60,27 радиуса Земли. Этот результат можно считать одним из замечательнейших достижений античной астрономии, несмотря на скудость наблюдательных данных, из которых его получили.

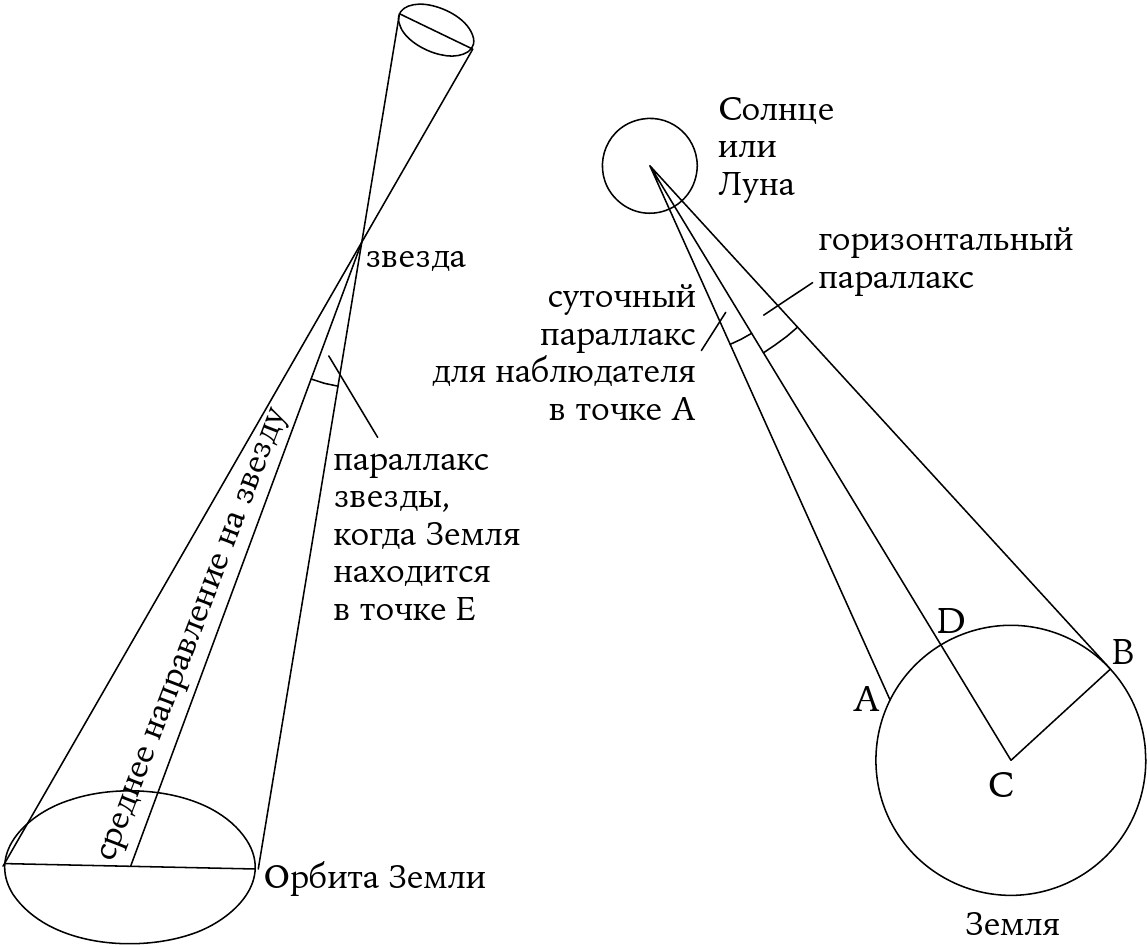
57

В общем случае «параллаксом» называют угол изменения видимого положения объекта при рассматривании его из двух различных пунктов. Забегая вперед, отметим, что, поскольку Земля движется по своей орбите вокруг Солнца, угол отклонения какой-либо близко расположенной звезды будет меняться таким образом, что она постепенно опишет на небе крошечный эллипс на фоне удаленных звезд (см. левую часть рисунка). Полный эллипс будет описан за год. Этот звездный параллакс (или «годичный параллакс») необходимо отличать от суточного параллакса, столь важного для внесения поправок в предвычисленные солнечные и лунные положения. Будучи рассчитанными на основе планетных моделей, они часто соотносятся с центром Земли. Однако наши наблюдения за Солнцем и Луной осуществляются из точки, отстоящей от центра Земли более чем на 6350 километров. Если мы наблюдаем какой-либо объект, когда он находится точно над нашей головой, то параллакс равен нулю, поскольку мы сами (в точке D на правой части рисунка), центр Земли и наблюдаемый объект располагаются на одной линии. Очевидно, что параллакс возрастает до максимума, когда объект находится вблизи горизонта, а мы – в точке B, как это показано на рисунке. Когда мы говорим о солнечном или лунном параллаксе в широком смысле, мы имеем в виду эти максимальные значения. Они, очевидно, напрямую связаны с расстояниями до рассматриваемых тел и с радиусом Земли, и начиная с XVIII в. было принято приводить их точные значения в расчете относительно экваториального радиуса. Так это слово вошло в устойчивый терминологический оборот: «средний экваториальный горизонтальный параллакс».

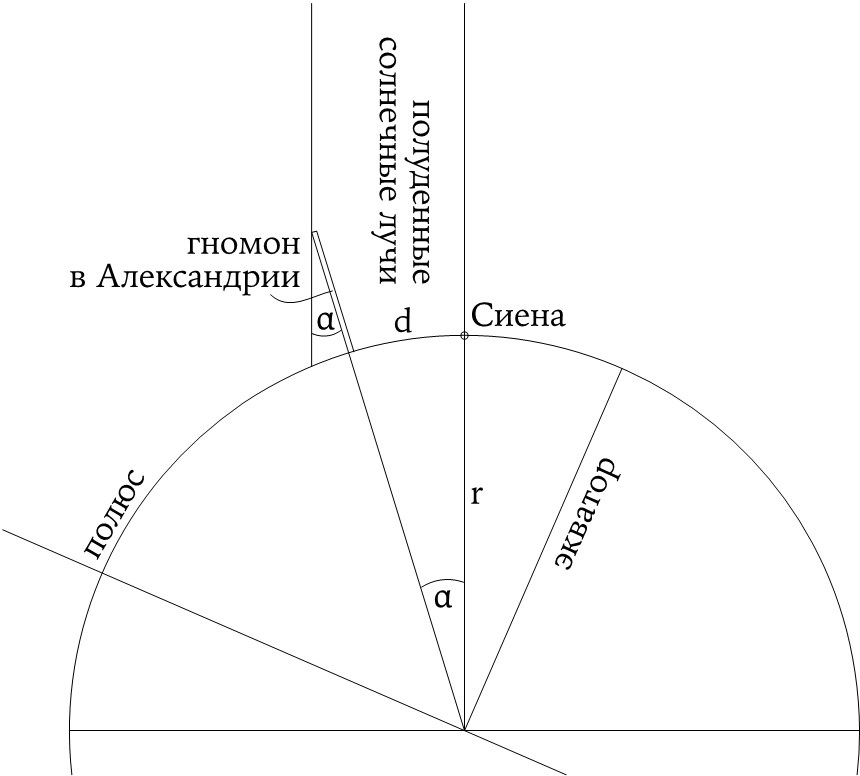
58

Согласно общему мнению, Эратосфен руководствовался сведениями о расположении полуденного Солнце в Сиене в день летнего солнцестояния прямо над головой, так что гномон не отбрасывает тени, а отблески солнечных лучей можно увидеть со дна самого глубокого колодца. Он измерил угловое зенитное расстояние Солнца (α) в Александрии, находящейся от Сиены на расстоянии (d), которое считалось равным 5000 стадий. Определив, что α составляет 1/50 часть окружности, он пришел к выводу: длина окружности Земли равна 250 000 стадий. Греческий стадий всегда считался равным 600 футам, но фут относится к слабо стандартизированным единицам. Оценивая результат Эратосфена в 48 000 километров, получаем значение, завышенное примерно на одну пятую часть. По-видимому, сам Эратосфен не был в нем уверен и пытался оценить его другими способами. Свидетельства моряков о том, что, на самом деле, расстояние до Сиены на одну пятую часть меньше принятого им за исходное, привели его к исправленному значению в 180 000 стадий.

Согласно Птолемею, Гиппарх не создал оригинальной модели планетного движения, но выступал критиком моделей своих предшественников. (Предположение Птолемея основывалось на отсутствии у Гиппарха сочинений по планетной теории. Якобы он, как приверженец истинного знания, не мог принять в качестве такового несовершенную модель.) Однако то, что Гиппарх составил сводку данных по вавилонским наблюдениям планет, возможно, внеся в нее свои собственные наблюдения, Птолемей использовал с максимальной эффективностью. Критическая проницательность Гиппарха сослужила и другую службу. В середине III в. до н. э. Эратосфен составил описание обитаемого мира, и именно этому якобы было посвящено его сочинение «Об измерении Земли», в настоящее время утраченное. Астрономический трактат Клеомеда, написанный шестью столетиями позже, содержит разъяснение, историческая достоверность которого сомнительна; в нем описывается, каким образом Эратосфен произвел оценку величины окружности Земли. Согласно описанию, этот несложный метод дал значение, равное 250 000 стадий (ил. 58). Гиппарх сурово раскритиковал многие положения этого сочинения. Однако ни одного из трудов Эратосфена не сохранилось, и у многих возникло сомнение – а искал ли он на самом деле длину окружности Земли или, как часто утверждается, всего лишь пытался измерить наклон эклиптики.

Заслуга Гиппарха перед греческой астрономией заключается в том, что он кардинальным образом поменял ее направленность, оставив в стороне качественные геометрические описания и полностью перейдя к эмпирической науке. Он так и не написал общего трактата, охватывающего всю науку в целом, а множество его небольших работ были утрачены, поскольку они оказались слишком сложными для заурядного читателя. Тем не менее его репутация в античном мире считалась довольно весомой. Птолемей извлек много пользы из его сочинений, хотя надо иметь в виду, что появившаяся недавно традиция называть Птолемея чуть ли не плагиатором Гиппарха вряд ли заслуживает серьезного рассмотрения. Как уже говорилось, отчетливые следы его влияния, в комплексе с другими сочинениями, написанными в стиле поздней (птолемеевской) традиции, достаточно легко обнаружить в индийской астрономии. Таким образом, в этом странном смешении событий Гиппарх предстает перед нами как бы в двух лицах.

АЛЕКСАНДРИЙЦЫ

В то самое время, когда вавилонское наследие оказывало все большее влияние на работу Гиппарха, в Египте пышно цвела месопотамская астрология. К этому моменту Египет уже эллинизировали (во всяком случае, внешне). Он был захвачен Александром Македонским (356–323 гг. до н. э.), а после его смерти передан в управление его сподвижникам и их потомкам. Несмотря на то что Александра воспитывал Аристотель, интересующие нас здесь интеллектуальные течения являлись следствием скорее его завоеваний, а не хорошего образования, которое он, по-видимому, получил. Александр имел веские основания считать себя величайшим полководцем античного мира. Унаследовав трон в возрасте двадцати лет, он захватил Македонию, Грецию и укрепил свои северные рубежи перед тем, как в 332 г. до н. э. пересечь Геллеспонт под предлогом освобождения греческих городов Малой Азии. Разгромив армии персов, он приостановил наступление в восточном направлении (на Месопотамию) до тех пор, пока не овладел Финикией, Палестиной и Египтом. Затем он двинулся на восток, разбил руководимых Дарием III персов на их собственной территории и двинулся в ту область, которую сегодня называют Туркестаном. Оттуда он пошел на Индию, расширив восточные границы своей империи до нижнего Инда. После того как он умер от лихорадки в возрасте всего лишь тридцати трех лет, его полководцы перессорились между собой и стали соперничать за захваченные им территории.

Мы уже говорили о последовавшем за этим правлении Селевкидов в Вавилонии. (Селевкиды – представители династии, основанной Селевком Никатором, одним из полководцев Александра. Они царствовали в обширном Сирийском регионе с 312 по 65 г. до н. э.) Город Александрию основал сам Александр, вероятно, как будущую столицу. Его друг и соратник Птолемей Сотер стал сатрапом Египта и, наконец, в 304 г. до н. э., провозгласил себя царем. Имя «Птолемей» носили все македонские цари Египта. Во время их правления старое местопребывание правительства перенесли из Мемфиса в Александрию, которая заметно выросла в своем значении и стала одним из наиболее влиятельных городов античного мира. Мы уже затрагивали вопросы, связанные с ее историей, в главе 2.

Александрия была важна не только как центр торговли, но и как центр обучения, она удерживала свои передовые позиции в регионе в течение всего периода римского правления. Во время царствования Сотера рядом с его дворцом основали два грандиозных учреждения – Музей и Библиотеку. Музей, который вскоре приобрел повсеместную известность, получил свое название в честь Муз, он служил домом для группы ученых, получавших жалованье и управляемых священником. Там читались лекции и проводились симпозиумы, и нередко в них принимали участие сами Птолемеи, вплоть до правления знаменитой Клеопатры – последней из их числа. В 47 г. до н. э., во время осады города Цезарем, грандиозный пожар спалил Александрийскую библиотеку, но в период римского правления ее фонды были восстановлены. На Музей злоключения посыпались значительно позже, уже после периода его интеллектуального расцвета, а именно – во II в. н. э. В III в. он претерпел много изменений, однако вплоть до конца IV в. в нем оставались выдающиеся ученые, последним из которых был Теон – отец знаменитой женщины-ученой Гипатии. И отец, и дочь считались сведущими в астрономии и других науках, и оба написали комментарии к сочинению Птолемея.

В течение столетий город служил проводником идей из соседних восточных регионов в Средиземноморье. Арабские завоеватели смогли, спустя определенное время, воспользоваться этой восточно-ориентированной интеллектуальной традицией, так что на довольно долгий срок этот город стал главным образом мусульманским центром. Даже правление Птолемеев подвергалось влиянию египетских идей, и большинство старых египетских религиозных культов возродилось, хотя служились они уже на греческом языке. И все же местный язык сохранялся лишь благодаря покровительству греческого правящего класса, особенно за пределами городов; впоследствии он снова вернулся к жизни в виде коптского языка.

О развитии греческой астрономии в период от Гиппарха до Птолемея известно на удивление мало; и поскольку Птолемей обычно ссылается на Гиппарха как на единственного своего авторитетного предшественника, за весь этот длительный период, как мы можем предположить, в области теории наблюдался лишь очень малый прогресс. Астрономия, безусловно, не умерла за это время. Мы не будем перечислять многочисленные мелкие свидетельства того, что она была очень даже жива, однако нельзя не упомянуть об одной неоценимой археологической находке – приводном астрономическом механизме, изготовленном из дерева и бронзы, остатки которого нашли в 1900 г. Они входили в состав сокровищ, находившихся на борту утонувшего судна, обнаруженного собирателем губок на морском дне, недалеко от Антикитеры – острова, находящегося между Критом и Пелопоннесом. Под обломками судна скрывалось много сокровищ, представлявших археологический интерес, особенно бронзовые и мраморные статуи, однако степень важности упомянутого механизма несколько иного порядка, поскольку он, в силу уникальных обстоятельств, остался в полной сохранности и был поразительно сложно устроен. Его досконально исследовали, особенно начиная с 1960‐х гг., и хотя различные объяснения слипшейся, проржавевшей массы находящихся в нем зубчатых колес и надписей на нем не во всем согласуются друг с другом, некоторые из его характеристик не вызывают сомнений.

Сегодня считается, что Антикитерский механизм датируется примерно концом II в. до н. э., хотя судно было построено между 80 и 60 гг. до н. э. Он приводился в действие вручную и размещался в деревянном корпусе размером примерно 315×190×100 миллиметров, с астрономическими и техническими надписями на передней и задней сторонах, фрагменты которых оказалось возможным расшифровать. В механизме обнаружили по меньшей мере тридцать зубчатых шестеренок. Самая большая из них обладает примерно такой же шириной, как и корпус, а самая маленькая – меньше сантиметра в поперечнике. Их зубцы имеют треугольную форму, что было типично для большинства зубчатых механизмов вплоть до Ренессанса, количество зубцов колеблется от 15 до 223. Механизм позволял рассчитывать и отображать календарную информацию, касающуюся Солнца и Луны, и его колесики предусматривали возможность расчета цикла затмений, состоящего из 223 лунных месяцев, а также цикла, где на 19 лет приходится 235 месяцев. (Мы уже встречались с этим ранее, говоря о неправильном отождествлении сароса с Метоновым циклом.) По-видимому, он должен был воспроизводить и Каллиппов цикл, представляющий собой не что иное, как четыре Метоновых цикла за вычетом одного дня – еще один цикл (также рассмотренный нами ранее), позволявший добиться лучшего согласования количества лет и месяцев, выраженных в целых числах. Последовательность из 235 месяцев размечена на спиральной шкале, снабженной замечательным устройством, в котором игла, размещенная в спиральном желобке, выполняла функцию указателя (стрелки), отмеряющего требуемую часть спиральной шкалы. Механизм указывал не только должным образом помеченные перемещения Солнца и Луны по эклиптике, лунные фазы, моменты возможного наступления лунных и солнечных затмений, но и, как полагают, предназначался для отображения некоторых планетных положений.