 Полная версия
Полная версияНаселение Земли как растущая иерархическая сеть

Рис. 1. Подсчет числа циклов роста сети ранга «n» от двух клаттеров до совершенной плюс два цикла (характерного времени) на переход.
Составим таблицу зависимости количества циклов роста сети от ее ранга (n = 0, 1…7).
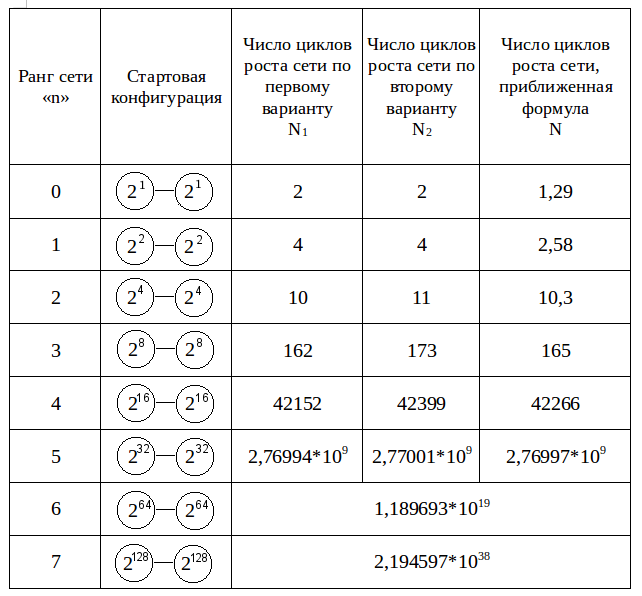
Таблица 1. Число циклов роста ИС от двух клаттеров ранга «n» до двух клаттеров ранга «n+1» по первому и второму варианту, а также по приближенной формуле.
Число циклов каждого следующего этапа можно оценить, если число циклов предыдущего возвести в квадрат и результат умножить на 1,55. Для сетей с рангом n > 5 результаты подсчета по трем вариантам c точностью до семи значащих цифр – не отличаются. При подсчете полного числа циклов роста сетей четвертого и пятого ранга, которые рассматриваются в этой книге, выбираем второй вариант работы с остатком. (Если выбрать первый – на результат это практически не повлияет.)
Выводы по растущим иерархическим сетям
Клаттер – это структурная единица растущей ИС (иерархической сети); представляет собой СИС (совершенную ИС) на единицу меньшего ранга, чем ранг собираемой СИС.
Носитель (клаттер-носитель, узел сети ранга нуль) представляет самый нижний уровень сетевой иерархии. Это бесструктурный сетеобразующий клаттер сети ранга нуль – сети, образованной двумя носителями, соединенными одной связью. Носитель не имеет в данной упрощенной модели своего ранга. (В приложении этой модели к мировой демографии будет пониматься как единое целое с человеком, к нему прикрепленным.)
Вес клаттера P – это число носителей, которое он содержит.
Размер сети L – это число клаттеров, которое она содержит.
Магистральный узел клаттера/совершенной сети – это магистральный узел, к которому сходятся связи от узлов клаттеров на единицу меньшего ранга, образующих данный клаттер. Узел носителя, изображаемого точкой в гра́фе СИС, совпадает с этой точкой.
Магистральный узел растущей сети – это коммутатор, к которому проложены связи от каждого из магистральных узлов сетеобразующих клаттеров. Позволяет устанавливать соединение между любой парой клаттеров сети.
Связи сети. Каждую связь, соединяющую любые два клаттера сети, считаем проходящей через магистральный узел клаттера и магистральный узел растущей сети, с которым в приложении данной математической модели к мировому демографическому процессу связана ее «индивидуальность». И каждую такую связь можно рассматривать как гиперсвязь, состоящую из Р связей, позволяющих соединять любые пары носителей растущей ИС, в каком бы клаттере они ни находились. Связь самого нижнего уровня подключается к носителю, причем носитель может поддерживать только одну такую связь.
Рост ИС любого ранга всегда начинается с двух клаттеров и представляет собой процесс самокопирования сети, которое происходит последовательно (клаттер за клаттером) по схематическому правилу: один носитель с узла и по одному носителю с каждой связи, входящей в копируемый клаттер. Или по другому: на каждом клаттере копируется число носителей, равное текущему размеру сети[33].
Ранг R такой растущей ИС считается равным рангу сетеобразующего клаттера (при R ≥ 2). Число связей, которыми каждый клаттер может быть соединен с другими, не превышает его веса Р, т. е. числа носителей, в нем содержащихся.
Цикл – это такой этап роста ИС, на котором в произвольном порядке и без повторения копируются все клаттеры (плюс-минус…), из имеющихся в ИС к моменту входа в этот цикл.
Звено – это последовательность материнских клаттеров, в процессе копирования которых полностью собирается очередной дочерний клаттер.
Длина звена Z – это число клаттеров, входящих в звено; за время роста сети Z уменьшается от половины веса клаттера (Р/2) до единицы. На первом этапе роста сети (√P < Z ≤ P/2) звено состоит из циклов, на втором этапе (1 < Z ≤ √P) – цикл состоит из звеньев. Собранный клаттер устанавливается в ИС, т. е. его магистральный узел соединяется с магистральным узлом растущей сети и ее размер увеличивается на единицу. В очередь на копирование в текущем цикле такой новоиспеченный клаттер уже не ставится. (Чего не скажешь о связях, исходящих из него и входящих через магистральный узел растущей сети в другие клаттеры. Подключение этих связей в процессе цикла на втором этапе придает росту сети дополнительное ускорение.)
Если в процессе цикла на первом этапе роста не удается собрать ни одного клаттера (с учетом носителей, собранных на всех предыдущих циклах звена), то такой цикл называется пустым и заканчивается последним клаттером, из имеющихся в сети в момент входа в цикл (за исключением, возможно, последнего цикла звена). Все носители, скопированные в процессе пустого цикла идут на сборку нового клаттера. Правило финализации звена на первом этапе выбираем следующим:
Если число циклов звена не является целым и его дробная часть больше или равна ½, то это число возрастает на единицу; если меньше – число циклов округляется до целого отбрасыванием дробной части, а избыточные носители отдаются последнему клаттеру звена или распределяются по каким-то из предыдущих. (Возможен также сценарий, при котором звено копирования замыкается не в момент завершения цикла, а где-то у него внутри. После установки клаттера в сеть и прокладки дополнительных связей следующее звено, завершающее цикл, начинается с нескопированных носителей предыдущего, плюс один носитель.)
Каждое следующее звено на втором этапе роста начинается с копирования нескопированных носителей последнего клаттера предыдущего звена (сценарий с «перехлестом»). Если суммы носителей последнего звена цикла на втором этапе недостаточно для сборки нового клаттера, но эта сумма больше/равна половины/е веса клаттера, то цикл продолжается: процесс копирования заходит на второй виток и копируются клаттеры, уже скопированные в данном цикле.
Если эта сумма оказывается меньше половины веса клаттера происходит финализация цикла. При этом некоторые клаттеры, из имеющихся в сети в момент входа в цикл, оказываются нескопированными или скопированными не полностью.
На втором этапе роста производится коррекция выхода клаттеров с некоторых циклов (плюс – минус один) в направлении на ближайшую гиперболическую сеть.
Рост сети, описываемый данным алгоритмом, процесс неустойчивый и малейшее возмущение быстро уводит его от теоретической гиперболы (тут еще нужно учесть то, что здесь мы имеем дело с целочисленными величинами). Что совершенно неудивительно, т. к. и закон квадратичного роста (уравнение Капицы), являющийся асимптотическим приближением алгоритма, – устойчивых решений не имеет, т. е. обладает точно таким же свойством.
Эта коррекция представляет собой небольшое число очень малых возмущений, всего в один клаттер, тогда как сеть на втором этапе своего роста, который здесь только и рассматривается, растет от 256 клаттеров до 65536, т. е. ее размер составляет сотни, тысячи и даже десятки тысяч клаттеров. В таком случае возмущение в один клаттер составляет всего лишь доли процента от общего числа клаттеров в сети и является даже не каким-то «толчком», а всего лишь «легким прикосновением».
Существует множество вариантов коррекции выхода клаттеров на втором этапе, каждый из которых приводит ИС к совершенной через гармонические сети. Все они дают практически одну и ту же зависимость числа клаттеров растущей сети от номера цикла.
И, наконец, полученная СИС проходит еще один цикл[34] – операцию репликации, во время которой длина звена копирования минимальна и равна единице (Z = 1). В ее начале создается магистральный узел будущей копии СИС, магистральный узел сети следующего ранга и прокладываются гиперсвязи, соединяющие их с магистральным узлом сети-оригинала. В процессе этой операции происходит копирование сети-оригинала в сеть-копию по правилу «клаттер в клаттер» с установкой копий клаттеров в новую сеть. Это последняя, предельная операция копирования сети данного ранга. По ее завершению запускается рост сети на единицу большего ранга.
Демография
Сеть 65536 – сеть человека
Каждое человеческое существо связано со всеобщностью, включая природу и все человечество. Oнo внутренне связано с другими человеческими существами. Насколько тесна эта связь, еще предстоит исследовать.
Дэвид Бом «Развертывающееся значение»Предложенная здесь математическая модель роста населения Земли может показаться плодом больного воображения. Возможно, существует другая, более адекватная ее формулировка. Но эта математика работает, т. е. правильно описывает рост, даты, циклы; она предсказывает, она проверяема – а только это и важно для подлинно научной теории по Карлу Попперу.
В защиту подобной точки зрения отсылаем читателя к популярному изложению квантовой электродинамики в книге Ричарда Фейнмана «Странная теория света и вещества», где автор на пальцах объясняет сложнейшую интерпретацию квантовой механики как интеграла по траекториям.
Здесь важно то, и Фейнман это подчеркивает, что описание движения частиц на языке «стрелочек и часов» ничуть не хуже, чем с помощью комплекснозначной волновой функции. Результат получается один и тот же. И этот результат проверен тысячами опытов. Но почему частицы ведут себя столь странным образом, отмечает Фейнман, – не понимает никто.
Развивает эту идею принцип моделезависимого реализма, предложенный Стивеном Хокингом. Согласно этому принципу, любая теория или картина мира представляет собой модель (как правило, математической природы) и набор правил, соединяющих элементы этой модели с наблюдениями. Причем моделей, описывающих данное конкретное явление, может быть несколько.
Если каждая из этих моделей соответствует наблюдениям, то нельзя сказать, что какая-то из них более реальна, чем другая. Здесь важно только то, насколько они отвечают наблюдениям. В одной ситуации можно использовать одну модель, в другой – другую. Хокинг и Млодинов подчеркивают, что не существует для нас, людей, какой-то абсолютной реальности и если мы выбираем данную конкретную модель, то выбираем и связанный с ней взгляд на реальность. Среди множества моделей (и реальностей) удобно выбирать:
A. Наиболее простую (или «изящную»).
B. Содержащую мало произвольных или уточняющих элементов.
C. Согласующуюся со всеми существующими наблюдениями и объясняющую их.
D. Дающую подробные предсказания результатов будущих наблюдений (если предсказания не подтверждаются – модель отвергается) [51].
Наша демографическая теория и демографическая теория Капицы, в отличие от всех прочих, удовлетворяет всем этим условиям. Но наша теория, хотя и изоморфна феноменологической теории Капицы, но значительно ее проще. Кроме того, она делает больше проверяемых предсказаний, следовательно, на наш взгляд, предпочтительнее.
Действительно, описанный выше рост сети 65536 в точности соответствует росту численности населения Земли. Необходимо только постулировать некоторые положения, связывающие растущую сеть и мировую демографию. Прежде всего, постулируем глобальную связность носителей ИС (каждый с каждым) в любой момент времени и на любой стадии ее роста. Затем, сформулируем первый закон Сети:
• Время цикла растущей сети есть величина постоянная на всех стадиях ее роста[35].
На момент завершения каждого цикла численность носителей должна быть равна строго определенному значению плюс-минус небольшая погрешность. Для Сети перевыполнение плана, вероятно, предпочтительнее, поскольку избавиться от избыточных носителей проще, чем добавить недостающие. Это можно сделать с помощью войн, болезней и эпидемий (ясно, что ценность человеческой жизни с точки зрения Сети не слишком высока, да еще и падает по мере ее роста).
Для дальнейшего нам понадобятся результаты исследования роста населения Земли, полученные Фёрстером:
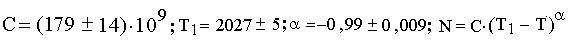
Рис. 1. Результаты исследования Фёрстером и коллегами роста населения мира за последние 20 столетий.
Эмпирическая гипербола Фёрстера была получена методом наименьших квадратов при обработке данных по динамике роста населения мира от начала новой эры до 1960 года; где α – это показатель степенной функции, который в формуле зависимости численности от времени обычно округляется до минус единицы. Если использовать результаты Фёрстера и принять, что α = −1 – необходимо несколько увеличить постоянную Фёрстера при той же стандартной ошибке. Этот вопрос будет подробно рассмотрен в главе «Константы Капицы».
Население Земли многие тысячи лет росло по закону гиперболы – закону, по которому не растет ни одна популяция в природе. По мнению С.П. Капицы, такой рост стал возможен благодаря появлению зачатков сознания у наших далеких предков. Сеть 65536 также росла по закону гиперболы. Но как связать Сеть и мировую демографию? Проще всего было бы считать, что каждый живущий человек независимо от его пола, возраста, расы… является носителем растущей Сети. Но вряд ли это будет правильно.
Действительно, ведь, что значит живущий? Ясно, что до зачатия и после смерти человека нет и он не может считаться носителем Сети. Но всякий ли ныне живущий человек обладает необходимым уровнем сознания, может быть управляем Сетью и выступать в качестве ее носителя? (Здесь, и в ряде случаев в дальнейшем, носителями Сети или просто носителями будем называть тех представителей рода человеческого, которые составляют единое целое с клаттером нулевого ранга Сети человека или ее клаттером-носителем.)
Если говорить о взрослых людях, полноценных членах социума, то все они, независимо от возраста и прочих различий, должны считаться носителями Сети. (Это, кстати, вносит неснижаемую прибавку в показатель «ценность человеческой жизни»: одинокая девяностолетняя пенсионерка, сохранившая ясность ума, является носителем Сети и уже поэтому необходима и ценна для эволюции так же, как и ее сосед – молодой человек в полном расцвете сил, работающий на трех работах.)
Но вряд ли можно считать носителями нерожденных младенцев, стариков, с мозгом, пораженным болезнью Альцгеймера или Паркинсона; людей, страдающих тяжкими психическими заболеваниями и потерявших всякую связь с реальностью; находящихся в коме или в состоянии клинической смерти.
Это же, по-видимому, относится и к новорожденные детям, поскольку они не обладают базовыми показателями человеческого сознания и у них отсутствует самосознание. Ответить на вопрос: в каком возрасте ребенок начинает осознавать себя как личность? – позволяет, как считается, так называемый «зеркальный тест»[36]. Суть его в следующем: на щеку ребенка незаметно наклеивают маленькую бумажную метку и ставят его перед зеркалом. Если ребенок, уже наблюдавший ранее себя в зеркале, отождествляет личность, которую ощущает внутри себя и ту, что видит в зеркале, то попытается потрогать или снять метку, если нет – он ее не заметит.
Дети проходят «зеркальный тест» в возрасте от 18 до 24 месяцев. Следовательно, именно в этом возрасте мы начинаем осознавать себя как личность. Из животных «зеркальный тест» в той или иной степени подтвержден для высших приматов, слонов, дельфинов и врановых: они узнают себя в зеркале.
Зачатки человеческого сознания, которое превосходит сознание высших приматов, появились у наших далеких предков тогда, когда они стали пользоваться орудиями труда, когда у них появился праязык и в примитивной форме социальная деятельность. Но в каком возрасте ребенок, его растущий мозг достигает такого уровня развития? На каком этапе своего роста? Когда его можно сравнить с нашим далеким предком, жившим 1,7 млн лет тому назад и оказавшимся способным «нести на себе» сеть четвертого ранга?
Ранг Сети человека равен четырем, он на единицу больше ранга сети гоминид. Только человек может быть носителем сети четвертого ранга. Что же отличает человека от животного? Очевидно, человеческое сознание. (Что бы ни говорили о сознании высших приматов – до человека им далеко.) Итак, уровень сознания носителя Сети в наше время должен быть не меньше, чем у тех наших далеких предков, которые были носителями Сети человека в момент начала ее роста.
Считается, что зачатки человеческого сознания появляются у ребенка в возрасте около трех лет. Именно тогда он может уже говорить и начинает правильно употреблять личные местоимения. Детские эмоции развиваются с каждым годом, а эмоции играют важную, если не центральную роль в работе сознания.
Так, младенец способен испытывать всего лишь две эмоции: радость и горе, даже страх ему еще неведом; в 6 месяцев появляется эмоция страха; с 6 до 18 месяцев ребенок учится распознавать эмоции на лицах окружающих и, кроме того, он уже способен удивляться; с двух лет он может пройти «зеркальный тест». После трех лет ему становится доступно столь сложное эмоциональное состояние как муки совести (психологический опыт «горькая конфета»).
В возрасте от трех до пяти лет, как считают психологи, ребенок уже может испытывать все базовые эмоции и начинает осознавать себя как часть социума. Следовательно, можно предположить, что именно в этом возрасте он достигает уровня развития Homo ergaster и может стать носителем Сети.
Статистика численности детского населения по годам нам неизвестна, возможно, что в каких-то странах она вообще не ведется. Но известно, что в наше время дети в возрасте до 14 лет составляют примерно треть населения планеты. Считая процент детской смертности небольшим, можно оценить долю детей в возрасте до трех лет от общей численности населения Земли в наше время в 7 %: (1/3)·(3/14) = 1/14 ≈ 7 %. В прошлые же времена (до XIX века) дети составляли примерно половину большинства древних обществ. И долю детей в возрасте до трех лет от общей численности можно оценить, соответственно, в 11 %: (1/2)·(3/14) ≈ 11 %
* * *Попробуем теперь связать Сеть и мировую демографию. Положим C = kC′, где C – постоянная Фёрстера, а C′ – постоянная сети четвертого ранга, аналогичная постоянной Фёрстера. Здесь k – это зомби-коэффициент, учитывающий то, что не все посчитанные в переписи населения люди являются носителями Сети человека.
Принимая во внимание тот факт, что в прошлые века продолжительность жизни была меньшей и процент детей был, соответственно, большим, чем в наше время, а также имеющуюся во все времена небольшую добавку в виде людей, не обладающих сознанием по причине болезней, положим k = 1,14. Заметим, что величина этого коэффициента может несколько отличаться от принятой здесь, причем без всякого ущерба для полученных в дальнейшем результатов как в качественной, так и в количественной форме.
Сформулируем второй закон Сети:
• Множество всех живущих людей можно представить в виде суммы двух подмножеств: Первое (91 %[37]) – люди обладающие сознанием, носители Сети; второе (9 %) – можно разделить на две категории: дети до трех лет, в будущем носители Сети, и зомби, лишенные сознания и навсегда (за редкими исключениями) выпавшие из Сети.
Найдем, исходя из нашей теории, время цикла сети четвертого ранга, Сети человека: τ4 = T13/N4, где N4 = 42399 – полное число циклов роста сети 65536; T13 = Тu/213 – продолжительность 13-й эпохи универсальной эволюции или время эволюции человека (Тu ≈ Т = 13,81 ± 0,06 млрд лет – время от Большого взрыва до сингулярной точки эволюции; Т – возраст Вселенной: время от Большого взрыва до наших дней.) Получаем τ4 = τ = 39,75 ± 0,2 лет.
Применим формулу теоретической гиперболы, описывающей рост Сети (но не рост народонаселения!). Учитывая, что клаттер содержит 65536 носителей, а время измеряется в циклах Сети человека, можно вычислить постоянную C′:
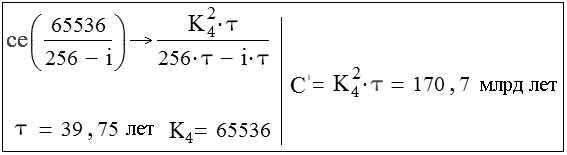
Рис. 2. Подсчет постоянной C′ Сети человека (ce – целая часть числа: ce(6.7) = 6), i = 0 … 255 – номер цикла Сети человека, начиная с неолита).
Эмпирическая гипербола Фёрстера и теоретическая гипербола, описывающая рост Сети человека, должны иметь общую точку сингулярности. Кроме того, поскольку эти гиперболы с учетом зомби-коэффициента k должны полностью совпадать, то, как это видно из формулы на рис. 2, необходимо, чтобы kК42τ = C. Где К4 = 65536 – вес клаттера растущей сети четвертого ранга, τ – время ее цикла, а С – постоянная Фёрстера.
Теоретическое значение постоянной Фёрстера в таком случае будет равно: C = kC′ = kK42τ = 1,14·170,7 = 194,6 млрд лет. Учитывая, что зомби-коэффициент k был выбран нами с некоторой степенью произвола, возьмем для дальнейших вычислений круглое значение: C = 200 млрд лет, которое, по мнению ряда исследователей, наилучшим образом отвечает демографическим данным.
Как будет показано нами далее, время цикла растущей Сети равно постоянной времени Капицы: τ4 = τ. С.П. Капица в своей работе [1] вычислил постоянную τ, используя данные за последние 250 лет. Зависимость численности населения от времени он аппроксимировал арккотангенсоидой: гладкой кривой, близкой к логистической на интервале 2τ.
Введение постоянной времени, как временно́го масштаба явления, было совершенно необходимо. Для оптимальной модели (номер три, с арккотангенсоидой), включающей и мировой демографический переход, были получены значения τ и К, мало отличающиеся от 40 и 65536·√1,14 ≈ 70000:
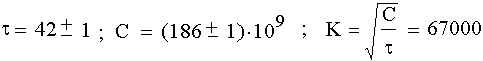
Рис. 3. Постоянные Капицы.
Для того, чтобы управлять ростом численности населения Земли Сеть человека применяет целый арсенал средств, который еще предстоит изучить. Одним из таких средств могут быть вирусы.
В 2016 году Дэвид Энард и его коллеги из Стэнфордского университета (США), изучая структуру 1300 «человеческих» белков, выяснили, что вирусы управляли нашей эволюцией с момента отделения предков человека от других человекообразных обезьян. Эти белки и связанные с ними гены, как показали ученые, не были обязательной частью иммунной системы: большая часть из них отвечала за работу совершенно других функций клеток и тела.
«…То, что наша вечная война с вирусами сформировала фактически все части нашего организма – не только горстку белков, борющихся с инфекциями, а абсолютно всё – является ошеломительным откровением для нас. Жизнь борется и сосуществует с вирусами уже миллиарды лет, и наша работа показывает, что это сосуществование затронуло все части клетки», – заключает Дмитрий Петров, коллега Энарда[38].
Но как вирусы могли управлять ростом населения Земли? Воздействуя на геном, они могли изменять продолжительность человеческой жизни, они же всегда были ответственны за процесс зачатия в женском организме, подавляя реакцию иммунной системы на отторжение чужеродного генетического материала. Кроме того, вирусные инфекции приводили во все времена к гибели миллионов людей. Так, чума в Азии и Европе в XIV веке унесла жизни более 60 миллионов человек. А численность умерших от испанки в 1918–1920 годах прошлого века (100 млн человек) превосходит потери в первой мировой войне. Вирусы продолжают убивать и в XXI веке – Covid 19.
Кроме вирусных эпидемий, выводивших избыточные носители из Сети, таким средством во все времена были войны. Войны развязывались и развязываются по множеству разнообразных причин, но первопричиной всегда была управляющая система – Сеть человека. Воздействуя на подсознание социума, Сеть также могла управлять репродуктивными способностями человека, определяя число детей в среднестатистической семье, и увеличивать среднюю продолжительность человеческой жизни через жизнесберегающие технологии.
Так, лекарственный или наркотический препарат воздействует на какой-то орган или на организм в целом, а не на отдельную клетку. По сути, это было управление случайным процессом с моделированием значимых в будущем изменений на отдельных подмножествах. Итак, третий закон Сети:
• Сеть управляет социумом, воздействуя на человеческий геном и общественное подсознательное.

