Население Земли как растущая иерархическая сеть

• начало эволюции ящеров 431/2 = 215,5 млн лет = 214 млн лет назад;

• появление плацентарных млекопитающих 215,5/2 = 107,7 млн лет = 106 млн лет назад;

• появление первых приматов 107,7/2 = 53,9 млн лет = 52,3 млн лет назад;

• появление предков человекообразных обезьян 53,9/2 = 27,0 млн лет = 25,3 млн лет назад;

• появление африканских гоминоидов 27,0/2 = 13,5 млн лет = 11,8 млн лет назад;

• появление первых гоминид 13,5/2 = 6,75 млн лет = 5,06 млн лет назад;

• появление линии представителей рода Homo, ведущей к современному человеку: 6,75/2 = 3,38 млн лет = 1,69 млн лет назад;

В итоге получим ряд (млн лет):

0, 1.69, 5.06, 11.8, 25.3, 52.3, 106, 214, 429, 861, 1724, 3451, 6903, 13810.

Эта последовательность задает времена начала эпох эволюции от старта эволюции вида, следующего за человеком, т. е. от настоящего времени, до Большого взрыва. Члены этого идеального ряда соответствуют в пределах небольшой погрешности фактической хронологии возникновения новых лидеров эволюции. (Откроем школьный учебник биологии и убедимся, что это так!)

Сравним времена, полученные по закону прогрессии и научные данные:

1.69, 5.06, 11.8, 25.3, 52.3, 106, 214, 429, 861, 1724, 3451, 6903, 13810.

1.80, 6.00, 12.0, 25.0, (55–58), 114, 235, 460, 840, 1850, 3500, (8000–10000), 13810.

И вычислим относительные погрешности:

6 %, 16 %, 1.7 %, 1.2 %, 6 %, 7 %, 11 %, 6.5 %, 2.6 %, 4.4 %, 9.2 %, 23 %, 0 %.

Какова вероятность случайного попадания ряда чисел, вычисленных по закону прогрессии, на действительные времена начала эпох с полученными погрешностями? Может быть, один шанс на миллион, а, может быть, и меньше[25]. На самом деле прогрессия эволюции − это уже реальность, а не гипотеза, − странно, что ее до сих пор не заметили.

В статье А.Д. Панова «Эволюция и проблема SETI» отмечено, что продолжительность последовательных фаз эволюции планетарной системы устойчиво сокращается от прошлого к настоящему. Эта последовательность переходов образует геометрическую прогрессию, причем ее знаменатель близок к числу Эйлера е = 2,718.

Если исходить из предлагаемой нами гипотезы, здесь у Панова перемешались две последовательности времен: биосферной эволюции и исторического процесса. Продолжительность периодов биосферной эволюции уменьшается по закону прогрессии эволюции.

Длительность исторических циклов, как интервалов между соседними гармоническими стадиями роста сети человека, в целом также уменьшается по закону, близкому к геометрической прогрессии. Поэтому и выявился закон прогрессии для времен, отмеряющих продолжительность фаз эволюции.

Однако моменты биосферных переходов в работе Панова связываются с какими-то нелепыми фазовыми переходами и катастрофическими событиями в биосфере, которые им соответствуют. Этот катастрофический подход, а главное неспособность автора ввести в рассмотрение отдельную прогрессию для исторического процесса привели к тому, что знаменатель прогрессии оказался завышенным (1/2.7, а не 1/2), и была неверно вычислена «конечная точка эволюции 4х-миллиардолетнего цикла».

Если начертить график зависимости времен появления новых лидеров универсальной эволюции в логарифмическом масштабе как функцию номера эпохи, то все эти точки будут почти точно лежать на прямой. У Панова они «рассыпаны» рядом с его прямой, что говорит о том, что моменты переходов были выбраны субъективно, хотя тенденция правильная.

Прогрессия универсальной эволюции объединяет эволюцию неживой материи, клеточную эволюцию, эволюцию животного и растительного мира, эволюцию человека и последующих видов. В связи с существованием прогрессии эволюции возможен иной, сетевой взгляд на эволюцию. Каждая эпоха связана со своим авангардом. Цель эволюции − новая авангардная система, которая возникает в конце эпохи.

Сеть, сопровождающая текущий авангард, выполняет план своего роста по циклам. Руководством для выполнения плана служит изначально заложенный в ней алгоритм, а хронометраж обеспечивает встроенный таймер. Рост сети и эволюция материального авангарда происходят синхронно и находятся в причинно-следственной зависимости: Сеть – причина. Совершенная стадия роста сети определяет конец эволюции текущего авангарда, а начало роста сети более высокого ранга соответствует началу эволюции следующего. Внутри эпохи значимые изменения авангардной системы эволюции приходятся на моменты прохождения сетью гармонических стадий своего роста.

* * *

Выпишем научные данные для времен появления авангардных систем эволюции и проанализируем этот ряд из 13-ти чисел. В результате получим, что он с высокой степенью достоверности образует геометрическую прогрессию со знаменателем 2.025, а первый член этой прогрессии равен 1,80 млн лет. (Начало отсчета t = 1,80 млн лет в будущем.)

Т. е. опять получаем, причем с хорошей точностью, время эволюции человека Thomo, но вычисленное другим способом. (Это время может быть получено через постоянную Капицы τ: Thomo = 39,75·42399 = 1,69 млн лет.) Может ли это быть простым совпадением?

Зная закон прогрессии, легко найти время эволюции вида, следующего за человеком. Оно равно: 1686/2 = 843 тыс. лет. В момент завершения глобального демографического перехода население Земли достигнет значения, равного примерно 9 млрд человек. В этот момент времени начнется рост сети «post Homo sapiens», сети пятого ранга, время цикла которой, как показывают расчеты, будет равно 160 минут. Это время, 1/9 земных суток, определяется рядом исследователей [18] как «ритм» абсолютного времени Космоса. Может ли это тоже быть простым совпадением?

Время неолита «post Homo sapiens», начало демографического перехода (момент начала репликации сети пятого ранга) и вся динамика роста этой сети во времени могут быть рассчитаны. После «post Homo sapiens» будет, видимо, еще только два вида. Это связано с фундаментальным ограничением на минимально возможный отрезок физического времени.

Из самого факта существования прогрессии эволюции следует синхронизм всех эволюционных процессов во Вселенной и антропный принцип. Действительно, перемещаясь по прогрессии эволюции в прошлое, доходим до Большого взрыва. Очевидно, что это событие явилось отправной точкой не только для земной, но и для любой другой эволюции. А синхронизм означает то, что все эволюционные процессы во Вселенной стартовали одновременно и имели единый алгоритм управляемой эволюции. Человек и его социальная ментальность – лишь одна из ступеней этой эволюции.

Они были «запланированы» еще в момент Большого взрыва или до того, так что точная подгонка физических и прочих законов к факту его существования не вызывает удивления. Синхронизм эволюционных процессов объясняет парадокс Ферми, который заключается в отсутствии признаков существования сверхмогучих цивилизаций.

Синхронизм приводит к тому, что братья по разуму переживают в настоящее время первый цикл демографического перехода и уж никак не доросли до межзвездных перелетов и астроинженерной деятельности. Молчание космоса как явление, подчеркивал И.С. Шкловский, представляет собой важнейший научный факт, и этот факт подтверждает предложенную здесь гипотезу.

Все синхронно протекающие эволюционные процессы, стартовавшие одновременно, должны одновременно и финишировать. В конце последней, шестнадцатой эпохи эволюции, через 1,5 млн лет от настоящего времени, в результате интеграции сетей седьмого ранга возникнет итоговая сеть восьмого ранга, которая «поглотит» весь энергетический ресурс Вселенной. Это будет «настоящая» сингулярность! Пространство «мгновенно» сдуется в точку, а финальная сеть в новом Большом взрыве распадется на мириады простейших.

Приведенные здесь правдоподобные рассуждения вряд ли можно назвать научными. Это уже не философия, но еще и не точная наука. Однако такая экстраполяция полностью отвечает финалистическому антропному принципу, в соответствии с которым материальная эволюция имеет смысл и цель. Очень хотелось бы в это верить!

Математика

Как известно, в любой науке столько истины – сколько в ней математики. Предлагаемая здесь теория описывает гиперболический рост населения мира на языке математики. Язык этот тяжел для восприятия, поэтому автор настоятельно рекомендует при первом чтении лишь просмотреть математические выкладки. Прочитать нужно только «Основные определения» и «Выводы по растущим иерархическим сетям».

Математика здесь несложная, но необычная; автор не знает аналогов, хотя, возможно, они и существуют. Все вставки – работающие листинги из системы MathCAD, так что тем, кто умеет с ней работать – легко все проверить.

Основные определения

Сетью называется граф, в котором вершины (узлы) соединены между собой связями, в данном случае двунаправленными (изображаемые ненаправленными) отрезками. Сеть, в которой каждый узел связан с каждым, называется гипертетраэдральной, а граф, обладающий таким свойством, – полным. (Только такие сети здесь и будем рассматривать.) Число связей, исходящих из одного узла, на единицу меньше числа узлов. Общее число связей S = N(N – 1)/2, например, сеть из пяти узлов содержит десять связей:

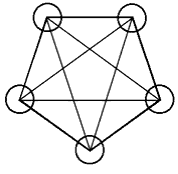
Рис. 1. Сеть, содержащая пять узлов; число связей S = 5·4/2 = 10.

Узлы сети могут быть соединены связями как непосредственно, так и через магистральный узел. Магистральный узел сети – это узел, к которому сходятся все связи растущей сети. Сеть, в которой число узлов равно 2R назовем гармонической, например, сеть из восьми узлов:

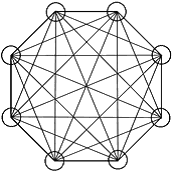
Рис. 2. Гармоническая сеть, содержащая 8 узлов; число связей равно 28.

Совершенной сетью назовем гармоническую сеть, содержащую число узлов, равное:

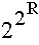
Где R – это ранг сети. Примеры совершенных сетей:

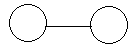
Рис. 3. R = 0, сеть содержит 2 узла, число связей равно единице.

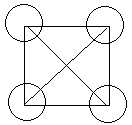
Рис. 4. R = 1, сеть содержит 4 узла, число связей равно шести.

Рис. 5. R = 2, сеть содержит 16 узлов, число связей равно 120.

Дадим рекурсивное определение совершенной иерархической сети (СИС). Совершенной иерархической сетью ранга R будем называть такую совершенную сеть ранга R, вершиной которой является СИС ранга R − 1. Эту сеть с рангом равным  R − 1 назовем сетеобразующим клаттером сети ранга R. Магистральный узел клаттера – это узел, к которому сходятся связи от магистральных узлов клаттеров на единицу меньшего ранга, составляющих данный клаттер. (Один из узлов-носителей каждого клаттера берет на себя функцию магистрального узла этого клаттера.)

Таким образом каждому узлу СИС сопоставляется также СИС, но на единицу меньшего ранга. Спускаясь по этой лестнице вниз, дойдем до первого этажа, точнее подвала (R = 0) в этой метафоре (если отождествлять ранг с этажом), который назовем уровнем носителя.

Чтобы рекурсия заработала дополнительно определим СИС ранга нуль как СИС, которая состоит из двух узлов, соединенных связью, которые назовем носителями. Под носителем при таком определении также понимается СИС (клаттер), но СИС эта не представляется в данной упрощенной модели как вершина иерархии сетей меньшего ранга, а рассматривается лишь как наименьшая, неделимая далее и не имеющая ранга структурная единица иерархической сети.

Узел-носитель (клаттер-носитель) есть величина постоянная; он обеспечивает функционирование сети и ее эволюцию. Чтобы связать сеть и мировую демографию будем считать, что этот узел-носитель не может существовать без своего «двойника», носителя-человека. Носитель-человек – это живущий и обладающий сознанием человек, временно «прикрепленный» к узлу-носителю сети и постоянно сменяющийся в процессе ее роста. Далее, для краткости изложения и в зависимости от контекста, будем называть единство узла-носителя и связанного с ним носителя-человека – носителем сети или просто носителем. Принимаем также, что связь самого нижнего уровня подключается к каждому узлу-носителю и к магистральному узлу клаттера ранга нуль, причем узел-носитель может поддерживать только одну такую связь.

Каждый узел-носитель рассматривается как уникальный, отличный от других носителей, клаттер сети ранга нуль. Выделенность носителя среди прочих СИС заключается в том, что рост сети любого ранга происходит путем копирования ее носителей (см. далее)[26].

Ранг СИС может принимать в данной модели следующие значения: R = 0, 1, 2… СИС минимального ранга – ранга нуль – это тот кирпичик, из которого строятся все остальные иерархические сети:

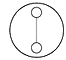
Рис. 6. СИС ранга нуль, R = 0.

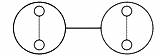
Рис. 7. СИС ранга один, R = 1.

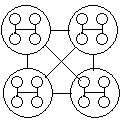
Рис. 8. СИС ранга два, R = 2.

Число клаттеров СИС равно числу носителей в ее клаттере (рис. 8). Гармонической иерархической сетью (ГИС) ранга R назовем такую иерархическую сеть, каждым клаттером которой является СИС ранга R, а число этих клаттеров равно двойке в некоторой степени: 2n, n = 1, 2… R – 1. Всякая СИС является так же и ГИС.

Если же число клаттеров иерархической сети не равно 2n, то такую сеть назовем несовершенной или просто иерархической сетью (ИС) ранга R[27]. Вес клаттера P определим как число носителей, которое он содержит:

Рис. 9. Вес клаттера сети ранга R.

Магистральный узел ИС/клаттера – это узел, к которому сходятся все связи от магистральных узлов слагающих ее/его клаттеров.  Размер сети L – это число клаттеров, которое она содержит. Число носителей ИС равно произведению веса клаттера на ее размер: N = PL. Число носителей СИС равно квадрату веса ее клаттера: Ns = P2. Пример:

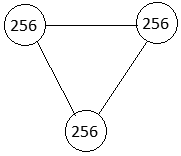
Рис. 10. ИС ранга 3, размером в три клаттера, вес каждого равен 256, число носителей 256·3 = 768. (Клаттеры для наглядности связаны непосредственно, а не через магистральный узел.)

Здесь мы дали определение биниальной иерархической сети (БИС), т. е. сети, клаттером которой является совершенная биниальная иерархическая сеть на единицу меньшего ранга. Теоретически можно рассмотреть тринитарную иерархическую сеть или даже сети более высокого порядка. Но, как утверждают сторонники биниальной парадигмы, приводя тому многочисленные примеры, именно дихотомическая (парная) структура прослеживается на всех иерархических уровнях организации макро и микромира.

Иначе говоря, все существующие природные объекты обнаруживают парность (биниальность, от лат. bini – пара), когда единое целое (атом, живая клетка, планета, звезда и т. д.) состоит только из двух частей (бинитаксонов), каждая из которых на нижеследующем иерархическом уровне вновь делится на две составляющие и т. д. Именно поэтому простейшая из возможных иерархических сетей, сеть минимального порядка, биниальная иерархическая сеть (в дальнейшем просто иерархическая сеть) лучше всего отвечает биниальной парадигме.

Далее, мы рассмотрим растущую, т. е. увеличивающую свой размер, а затем и ранг ИС и подберем для нее такой алгоритм роста, который наилучшим образом отвечает идее эволюции.

Растущая иерархическая сеть

Растущая ИС – это сеть, число клаттеров которой растет согласно некоторому алгоритму. Этот рост будем связывать с операцией самокопирования ИС, которая происходит циклически. Цикл самокопирования ИС определим как такой этап ее роста, на котором копируются все (в произвольном порядке и без повторения) клаттеры, имеющиеся в ней к моменту входа в этот цикл[28]. Звено самокопирования ИС определим как такую последовательность клаттеров, на которой собирается и устанавливается в сеть еще один новый клаттер. Длина звена Z – это количество клаттеров, входящих в звено.

Операция самокопирования заключается в следующем: ИС последовательно (клаттер за клаттером) копирует носителями по определенному правилу текущее число клаттеров[29], собирает новый, устанавливает его в себя и увеличивает свой размер на единицу. Правило самокопирования выберем таким:

Новый клаттер собирается в процессе копирования носителями связей каждого клаттера и его магистрального узла. Т. е. (чисто схематически)  копируется магистральный узел сетеобразующего клаттера[30] и каждая входящая в него связь. Можно сформулировать иначе: с каждого сетеобразующего клаттера в текущем цикле копируется и устанавливается в собираемый клаттер число носителей, равное текущему размеру сети[31].

Клаттеры, собранные внутри цикла на втором этапе роста сети (см. далее), в очередь на копирование в текущем цикле не ставятся. Процесс копирования клаттеров на всех этапах роста сети можно представить следующим образом: сначала создается копия магистрального узла клаттера и соединяется с магистральным узлом растущей сети. Затем копируются магистральные узлы клаттеров нижнего уровня, составляющих копируемый клаттер, и только после этого последовательно копируются все остальные узлы (носители) и через магистральные узлы клаттеров нижнего уровня подключаются к магистральному узлу собираемого клаттера. При таком сценарии каждый вновь поступающий носитель оказывается сразу же подключенным ко всей сети.

Почему выбирается именно такой алгоритм? В соответствии с системным подходом сложность, эволюционная зрелость любой развивающейся системы определяется, прежде всего, ее связями. Если связи растущей системы однородны, то скорость ее эволюции (в простейшем случае роста) зависит только от их числа. Чем больше связей – тем быстрее эволюционирует, развивается, растет система.

Поэтому логично постулировать, что прирост клаттеров-носителей с каждого сетеобразующего клаттера, получаемый в процессе его копирования, должен быть пропорционален, а в простейшем случае просто равен числу его связей с другими клаттерами. И в этом простейшем случае оказывается, что алгоритм хорошо описывает рост Сети человека на втором этапе (см. далее) и, соответственно, гиперболический рост населения мира после неолита.

Но если применить его при описании роста сети на первом этапе (см. далее) и, соответственно, роста численности первых архантропов, то получим, что положение циклов эволюции на оси времени и время появления рода Homo, рассчитанные теоретически, не согласуются с данными палеодемографии.

Однако, если слегка модифицировать алгоритм так, чтобы при подсчете прироста носителей с каждого клаттера добавлять к числу его связей единицу, формально полагая, что копируются не только входящие в клаттер связи, но и его магистральный узел (т. е., если считать, что число копий клаттеров-носителей, снимаемых с каждого сетеобразующего клаттера за цикл, равно текущему размеру сети), что совершенно несущественно на втором этапе, когда таких клаттеров и, соответственно, подключенных к ним связей сотни, тысячи и даже десятки тысяч – то вот такой алгоритм будет правильно описывать эволюцию, историю и рост населения мира на всех этапах[33].

Дополнительно хотелось бы отметить, что выбранный алгоритм при учете правила финализации звена и цикла  (которое, хотя и может быть сформулировано по-разному, но не оказывает практически никакого влияния на результат) хорош уже тем, что чрезвычайно прост и эстетичен.

Даже если бы оказалось, что он не имеет никакого отношения к реальному росту населения Земли, модель все равно заслуживала бы внимания уже только потому, что при минимальных предпосылках позволяет правильно описывать как количественно, так и качественно динамику роста (начало роста, неолит, переход), а также цикличность глобального развития: сокращающиеся по закону прогрессии циклы эволюции, глобальные исторические и экономические циклы.

В таком случае модель можно было бы рассматривать как простую и эффективную схему, позволяющую систематизировать многочисленные демографические и исторические данные. Но вопросов о том, почему это стало возможным, почему такая простая модель столь точно соответствует действительности, почему она вмещает в себя такой большой объем информации, случайно ли? – все равно не избежать.

* * *

Применим данный алгоритм для описания роста биниальной иерархической сети ранга R. Будем считать, что рост этот всегда начинается с двух клаттеров. В таком случае его можно разбить на три качественно отличающихся этапа:

Первый этап (√P < Z ≤ P/2)  – рост от двух до √P клаттеров. (P = 2^(2^R) – вес клаттера или число носителей, которое он содержит. Z  – длина звена копирования или число клаттеров, в процессе копирования которых собирается очередной дочерний клаттер.)

Второй этап  (1 < Z ≤ √P) – рост от √P до Р клаттеров. На втором этапе новоиспеченные клаттеры в сеть включаются в процессе их сборки, но в текущем цикле в очередь на копирование не ставятся, копируются только подключенные  к ним связи[10].

Третий этап (Z = 1) – операция репликации: создание одной копии полученной совершенной сети[9].

На первом этапе звено состоит из повторяющихся циклов, причем каждое последующее звено короче предыдущего; на втором этапе – цикл состоит из некоторого числа укорачивающихся звеньев. Длина звена за весь период роста уменьшается от P/2 до единицы.

* * *

Рассмотрим теперь все этапы роста ИС на примере сети ранга 3. Вес клаттера Р = 2^(2^3) = 28 = 256, т. е. число носителей в клаттере равно 256. Корень из веса √Р = 16. Стартовый размер сети полагаем равным двум.

Первый этап роста сети  (16 < Z ≤ 128)

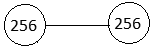
Рис. 1. Старт роста сети 256.

Алгоритм копирования следующий: на каждую связь и на каждый магистральный узел копируемого клаттера устанавливается носитель. Связи клаттера соединяют все другие его узлы с магистральным, а тот, в свою очередь, соединен с  магистральным узлом сети. Но в приведенных схемах для наглядности будем изображать связи отрезками, соединяющими клаттеры. Кроме того, будем безо всякого ущерба для математики считать, что собираемый клаттер не подключен к сети и устанавливается в нее лишь в момент его полной сборки.

В данном случае связь одна, магистральный узел всегда один. Всего на клаттере копируем два носителя. Нужно собрать 256 носителей, поэтому переходим к следующему клаттеру и копируем еще два носителя.

Собрали четыре носителя. Цикл закончился, он оказался пустым, т. к. все имеющиеся на момент входа в цикл клаттеры скопированы, а новый собрать не удалось. Всего имеем 63 пустых цикла. На 64-м цикле и 128-ой по счету операции копирования (длина звена составила 128 клаттеров) получаем 256 носителей. Сборка клаттера завершена; устанавливаем его в сеть, прокладываем связи.

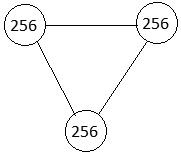
Рис. 2. Собран первый клаттер.

Теперь каждый клаттер имеет уже две входящие в него связи, поэтому копируем по три носителя на клаттере или 32 = 9 девять за цикл. Число 256 не делится нацело на 9, как в предыдущем случае, и для создания четвертого клаттера потребуется 256/9 = 28 полных циклов, плюс 4/9 цикла; поэтому последний 29-й цикл будет неполным, т. к. первый клаттер на нем будет скопирован полностью (3 носителя), второй – частично (один носитель), а третий – останется нескопированным. И здесь возникает неопределенность в вопросе как начинать следующее звено: с продолжения предыдущего неполного цикла или с начала нового?

Непонятно также следует ли учитывать неполный цикл при подсчете общего числа циклов звена. Ведь в приложении этой математической модели к росту населения Земли наиболее важными законами роста являются закон постоянства времени цикла и синхронности (синфазности) роста и развития. Неясно, правда, должна ли такая синхронность (синфазность) роста строго выполняться для каждого цикла или только для моментов гармонического достижения; а может быть синхронно должен завершаться только последний цикл роста сети данного ранга, на момент окончания которого она становится совершенной? (Учитывая факт гиперболического роста населения мира, этот вариант вряд ли следует принимать во внимание.)