Население Земли как растущая иерархическая сеть

Но вернемся к гиперболе. Если бы получилось так, что показатель p оказался близок к единице, но не равен ей (p ≠ 1); близок в том смысле, что в результате обработки большого объема данных доверительный интервал для него оказался небольшим и включающим целочисленное значение, в данном случае единицу, то соображения размерности позволили бы сразу же считать, что p = 1.

Иначе пришлось бы вводить фундаментальную константу с непонятной и изменяющейся по мере поступления новых данных размерностью. У Фёрстера p принадлежит интервалу [0.981, 0.999] и этот интервал немного, на одну тысячную, «не дотягивает» до единицы, но все равно нужно положить p = 1, т. к. его границы выбираются по предзаданной вероятности.

Вывод здесь простой: закон роста населения Земли не мог быть «примерно» гиперболическим с нецелым, близким к единице показателем p и говорить о гиперболическом тренде, гиперболической тенденции и «надэкспоненциальном» росте в применении к мировому демографическому процессу – неверно в принципе.

И еще один важный момент. Что означает утверждение о том, что в течение всей эпохи гиперболического роста показатель p в формуле закона роста был равен единице?

Оно не означает, конечно, что рост всегда шел в точности по гиперболе Фёрстера, что естественный прирост населения мира причинно определялся численностью и был в любой момент времени пропорционален квадрату численности. Даже если бы это было так – рост все равно не был бы гиперболическим по причине его неустойчивости.

По нашему мнению, такой рост может быть представлен как нестационарный случайный процесс похожий на случайное блуждание по вертикали, направленное на гиперболу роста, с постоянным дрейфом по горизонтали в координатах время-численность на графике гиперболы демографического роста.

Показатель p в таком случае в точности равен единице лишь в том смысле, что это случайное блуждание во все времена каким-то непонятным образом направлялось на теоретическую гиперболу демографического роста, у которой p = 1. Именно поэтому при обработке данных по методу наименьших квадратов усредненный показатель p и оказался столь близок к единице. Итак, почему p = 1? Тому есть две причины:

1. Работа Фёрстера и его коллег, результаты которой считаются общепризнанными и из которой следует, что p = 1 с точностью до одного процента.

2. Соображения размерности: постоянная Фёрстера должна иметь размерность времени, а это возможно лишь при p = 1.

Теперь о потере точности при определении С.П. Капицей постоянных τ и К. По нашему мнению, такая потеря произошла при замене p = 0.99 (усредненный показатель по Фёрстеру) на целочисленный показатель p = 1.

«Как же так!» – возможно, удивится читатель. Только что доказали, что показатель p в законе Фёрстера должен быть в точности равен единице, а теперь утверждаем обратное?

Противоречия здесь нет, т. к. причинный динамический закон, благодаря которому эмпирический закон роста численности от времени оказался столь близок к гиперболическому с p = 1, предполагает существование теоретической гиперболы, показатель которой в точности равен единице.

Говоря о законе Фёрстера, мы и имеем в виду эту теоретическую, «идеальную» гиперболу. Однако при подсчете постоянных τ и К нужно пользоваться не теоретическим, а эмпирическим законом, т. е. гиперболической зависимостью с показателем p = 0.99, вычисленным по методу наименьших квадратов, и сейчас мы это докажем.

Существует семейство гипербол, почти столь же хорошо отвечающих демографическим данным за последние двадцать столетий, как и гипербола Фёрстера, каждую из которых можно полностью определить с помощью трех параметров [C, p, to][100].

Точность переменной численность населения Земли N(t) при ее вычислении по формуле Фёрстера менее всего зависит от даты сингулярности to, т. к. она определена Фёрстером и его коллегами с очень хорошей (в несколько лет) точностью.

Следовательно, даже в первой половине ХХ века любая вариация to в пределах доверительного интервала практически не влияет на результат. Здесь еще нужно учесть то, что динамика изменения численности населения мира даже в ХХ веке известна лишь с точностью до нескольких процентов, а также и то, что во второй половине ХХ века начался демографический переход и формула Фёрстера перестала правильно описывать рост.

Из двух оставшихся констант [C, p] наиболее важной – в плане ее максимально точного определения – является показатель степенной зависимости р (степенная функция гораздо более чувствительна к относительному изменению ее показателя по сравнению с аналогичным изменением мультипликативной константы), который характеризует «крутизну» гиперболы. Даже небольшая, в один-два процента, его вариация может существенно повлиять на результат, причем во всем диапазоне исторического времени.

Изменение постоянной Фёрстера С определяет равномерное растяжение (сжатие) исходной гиперболы роста от/к оси времени, и поэтому точность в ее определении одинаково важна при подсчете численности во все времена. Точность, с которой могут быть определены постоянные Капицы K и τ, напрямую зависит от точности, с которой вычислена пара [C,p] в соответствии с условием С = Mτp = K2τp. (Это условие определяет безразмерность переменной N(t) в уравнении Фёрстера N = C/(t0– t)p.)

Хотя действительный (теоретический) закон роста, как мы показали ранее, – это гипербола с целочисленным показателем p = 1, но если в результате обработки демографических данных по методу наименьших квадратов средняя аппроксимирующая гипербола получилась с дробным показателем, то при определении К и τ нужно исходить из обобщенного условия С = Mτp = K2τp. Использовать для этой цели уравнение С = K2τ, как это делает С.П. Капица, – представляется ошибочным.

Почему это так? Дело в том, что эмпирическая гипербола, заданная тройкой [C, p, to] меньше отличается (отстоит на меньшее расстояние) от теоретической гиперболы, соответствующей закону гиперболического роста [C', 1, to'] (где C' и to' неизвестны), чем гипербола, определяемая тройкой [C, 1, to], у которой p = 1, а С и to остаются теми же, что у эмпирической гиперболы или каким-то случайным образом варьируются.

Поэтому характерное время и характерная численность (сторонние, не связанные со степенным законом роста) для обобщенного закона с нецелочисленным показателем р, закона, определяющего гиперболу [C, p, to], ближе (по сравнению с законом [C, 1, to]) к тем, что могли бы быть вычислены для теоретического закона гиперболического роста с целочисленным показателем p = 1, будь этот «истинный» закон ([C', 1, to']) известен.

Например, если бы удалось каким-то образом довольно точно оценить характерное время τ, то характерную численность K следовало бы вычислять в соответствии с условием С = K2τp, а не с условием С = K2τ.

Допустим, к примеру, что характерное время τ связано с каким-то циклическим историческим процессом и длительность этого цикла известна с хорошей точностью. Или же, никакой такой цикл неизвестен, а момент отхода роста от гиперболы найден с достаточно хорошей точностью, исходя из анализа общей его динамики во второй половине ХХ века.

В таком случае значение константы K следует искать в соответствии с эмпирической зависимостью Фёрстера рис. 1: N(to – τ) = K2= C/τp, где C = 179 млрд, p = 0.99, поскольку эта зависимость позволяет с наибольшей точностью вычислять полное число живущих в каждый год от начала новой эры до начала перехода. А не по формуле Капицы: N(to – τ) = K2 = C/τ, где C = 163 млрд, которая была получена в результате округления показателя р до единицы. [21]

Поэтому значение численности на момент начала перехода, вычисленное по эмпирической формуле Фёрстера, будет более точным, чем в соответствии с феноменологическим уравнением Капицы. Кроме того, об этом же говорит и теория размерностей. Нельзя определять характерную численность, исходя из условия К2 = C/τ, как это делает С.П. Капица, поскольку постоянная С в работе Фёрстера имеет размерность год0.99.

Так, если взять C = 186 млрд, К = 67000, как он полагал в своей первой статье 1992 года, то при р = 1 получаем τ = 41.4 года, а при р = 0.99 – τ = 43.0 года. Если же взять С = 163 млрд и К = 60100, как в его последней работе 2010 года [21], то при р = 1, τ = 45.2 года, а при р = 0.99, τ = 46.9 лет.

Разница для характерного времени в обоих случаях слишком велика, чтобы пользоваться формулой С = K2τ вместо формулы С = K2τp. Неоднократно изменяя свои константы K и τ, С.П. Капица никогда не подбирает для каждой такой пары наиболее подходящий показатель степенной функции р, считая, что он во всех случаях равен единице. И это, на наш взгляд, может рассматриваться как довольно серьезная ошибка. В книге «Парадоксы роста. Законы развития человечества» на стр. 170 читаем:

«При обращении к последним данным демографии были получены уточненные значения постоянных: С = 163 млрд, и К = 60100, τ = 45 лет; K = (C/τ)0.5».

При этом подразумевается, что p = 1; на самом же деле значению С = 163 млрд лет в семейство гипербол, аналогичных гиперболе Фёрстера, полученных по методу наименьших квадратов, должен соответствовать некий неизвестный показатель р, значение которого при подсчете своих постоянных С.П. Капица никак не учитывает. Можно ли в таком случае доверять тем оценкам для K и τ, которые он получил?

По неясным причинам С.П. Капица не связывает характерное время τ и характерную численность K с моментом начала перехода, что также является, по нашему мнению, большой ошибкой. (Скорее всего, по причине неверного определения начала перехода через мгновенную скорость роста численности dN/dt.) Кроме того, совершенно непонятно откуда вообще взялось значение С = 163 млрд лет, которое без всякого обоснования и каких-либо объяснений появляется в его последней работе [21]. Оно совершенно не согласуется с результатами работы Фёрстера и приведенными ниже оценками.

* * *

Определим константы Капицы, исходя из нашей гипотезы: характерная численность Капицы K = √kK4= √1,14·216 ≈ 70000 (полагаем k = 1.14, точность К зависит от точности в определении зомби-коэффициента k, доверительный интервал для которого нам неизвестен); характерное время находим по формуле τ = T13/N4. Где T13 – продолжительность 13-й эпохи универсальной эволюции или время эволюции человека; N4 – полное число циклов роста сети четвертого ранга, сети 65536; T13 = Тu/213, Тu = 13.81 ± 0.06 млрд лет – время эволюции Вселенной, N4= 42399. Получаем τ = 39.75 ± 0.20 лет.

* * *

В заключение рассмотрим вопрос о точности, с которой известна постоянная Фёрстера.

1. Согласно расчетам Фёрстера и его коллег, значение постоянной С равно 179 ± 14 млрд лет. Но это ее значение справедливо лишь для эмпирической гиперболы с показателем p = 0.99. Если же положить p = 1, что соответствует теоретической гиперболе и, как мы это показали ранее, действительному закону роста, то значение постоянной Фёрстера должно быть несколько увеличено.

На пальцах это можно объяснить так: гипербола y = C/x2 при x > 1 ближе «прижимается» к оси 0X чем гипербола y = C/x и чтобы вернуть ее на позицию максимально близкую (на некотором интервале) к y = C/x нужно несколько увеличить С. В нашем случае гипербола с p = 0.99 отстоит на наименьшее расстояние от всех точек плоскости (Ni, ti), отвечающих данным мировой демографии. Гиперболу с p = 1 нужно немного «приподнять» над осью 0t для того, чтобы максимально сблизить с оптимальной гиперболой с p = 0.99, т. е. немного увеличить С.

Авторы статьи «Судный день: Пятница, 13 ноября 2026 года» (Doomsday: Friday, 13 November, A.D. 2026) использовали в своих вычислениях 24 опорных значения времени и численности, полученные из большого числа источников разной степени надежности, однако никакие из них приведены не были. Так как воспользоваться этими данными и определить на их основе постоянную С при p = 1 невозможно, оценить ее можно только исходя непосредственно из результатов исследования. Для этого необходимо подобрать такую гиперболу с целочисленным p = 1, которая отстоит от эмпирической гиперболы Фёрстера на наименьшее «расстояние»:

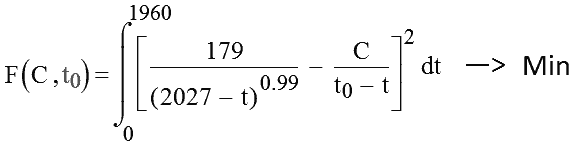
Рис. 1. Определение постоянной Фёрстера С для гиперболы с целочисленным показателем, исходя из условия минимальности «расстояния» между гиперболой с p = 1 и гиперболой Фёрстера с p = 0.99.

Значение С, которое является решением данной вариационной задачи, равно 188 млрд лет с точностью до одного-двух процентов, независимо от значения t0 в интервале [2022, 2028]. Поскольку у Фёрстера постоянная С определена с точностью 8 %, то эту же точность (как минимум) следует принять и для ее модифицированного значения. (Это и подобные ему определения постоянной С, основанные на усредненных значениях t0 и р, не могут, конечно, считаться математически строгими. Но позволяют, тем не менее, оценить ее примерное значение, которое должно быть на несколько процентов больше, чем 179 млрд у Фёрстера.)

2. Для непосредственного вычисления постоянной С при р = 1 воспользуемся данными по росту населения Земли, представленными в работе [40] Остина и Брюэра (A.L. Austin and J.W. Brewer). Хотя точек N(ti) у них, в отличие от работы Фёрстера и коллег, всего только 12 – все они взяты из трех авторитетных и признанных источников.

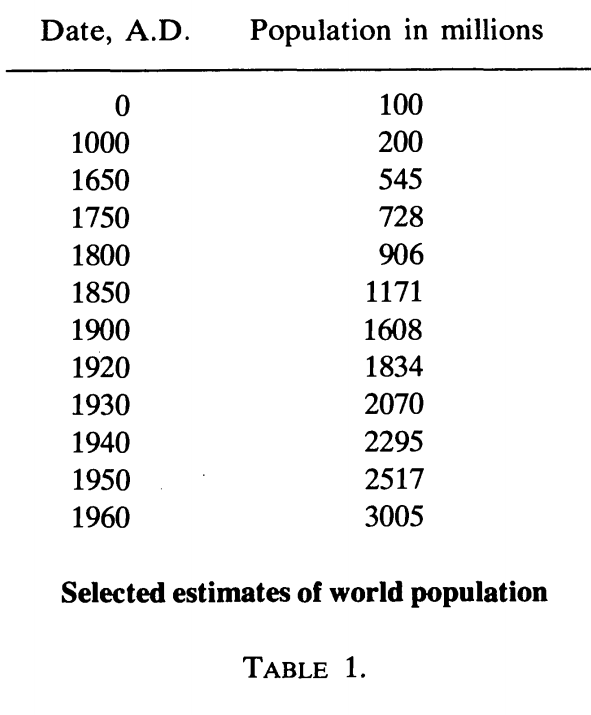
Таблица 1. Данные по населению мира от начала новой эры до 1960 года согласно A.L. Austin and J.W. Brewer [40].

Добавим еще одну точку N(1982) = 4.72 млрд, которая соответствует и теоретической гиперболе, и данным мировой демографии и обработаем все эти данные методом наименьших квадратов. В результате получим (в предположении p = 1, t0 = 2022) C = 194.3 млрд лет. Поскольку объем данных, использованных здесь, невелик – надежность этой оценки остается под вопросом.

3. Мак-Эведи, Джоунс и Кремер выполнили собственный расчет, включив данные по неолиту и верхнему палеолиту. Значение постоянной Фёрстера С оказалось равным 189.6 млрд лет (p = 1, t0 = 2022) [13].

4. Примерно такое же значение для постоянной С находим и в работе [1] С.П. Капицы. Особенность его оценки, как мы уже отмечали ранее, заключается в том, что он определил постоянную Фёрстера, используя данные только за последние 250 лет с учетом демографического перехода. (Понятно, что это значение не является достаточно надежным, поскольку не учитывает данные за прошли века и тысячелетия.) В результате был получен следующий результат: C = K2τ = 186 ± 1 млрд лет (τ = 42 ± 1, К = 67000, p = 1, t0 = 2027 ± 1).

5. И, наконец, определим значение постоянной Фёрстера на основе нашей модели, вычисляя ее по формуле C = kK42τ. Точность, с которой может быть определена С, сильно зависит от усредненного зомби-коэффициента k, значение которого подбирается исходя из критерия близости теоретической гиперболы к данным мировой демографии. При k =1.14  C = 1.14·655362·40 = 196 ± ? млрд лет.

Итак, для постоянной Фёрстера имеем пять довольно близких, в первом приближении независимых оценок:

1. Исходя из результатов работы Фёрстера и его коллег: С = 188 млрд лет.

2. Расчет на основе данных взятых у Остина и Брауэра: С = 194 млрд лет.

3. Работа Мак-Эведи, Джоунса и Кремера: С = 190 млрд лет.

4. Модель С.П. Капицы: С = 186 млрд лет.

5. Сетевая модель: С = 196 млрд лет.

Рассматривая эти результаты как ряд последовательных, независимых измерений величины С, для ее среднего значения и среднеквадратического отклонения получаем (при условии р = 1, t0 = 2022): С = 191 ± 4 млрд лет. Поскольку  точность этой оценки вряд ли может считаться удовлетворительной (по причине малого объема выборки), величина погрешности, с которой может быть определена постоянная С, остается неизвестной. Возможно ли вообще когда-либо решить эту задачу, учитывая значительные пробелы и неточности в данных по численности населения Земли?

Финальность как движущая сила Универсальной эволюции

История не может иметь смысла, если она никогда не окончится, если не будет конца; смысл истории и есть движение к концу, к завершению, к исходу.

Николай Бердяев

Введение

Современный научный подход к вопросам эволюции и развития опирается на представление о самоорганизации материи и самодостаточности элементарных законов с преддетерминацией, т. е. простейших физических законов, для объяснения всего спектра явлений материального мира, в том числе проблемы происхождения жизни, сознания, природы социальных явлений. Но так ли это?

Имеет ли финализм как эвристическая позиция право на жизнь? Целью нашего исследования является доказательство того, что финализм, как основа для описания универсальной эволюции, полностью соответствует всем имеющимся натурфилософским, антропологическим и историческим данным о природе, человеке и обществе.

Понятия финальности связано с философским системами, которые рассматривают исторический процесс как движение, имеющее конечную цель, благодаря которой обретают смысл реальные исторические события. История описывается как процесс, направляемый имманентно присущей ему целью.

Идея «Конца истории» является детерминистской и телеологической философской идеей, представляющей историю как линейный процесс и придающей ему смысл и цель. По Гегелю, история есть процесс самореализации высшего Духа (или Сознания). Осуществляя свои цели, абсолютный Разум управляет вещами событиями и людьми, хитроумно используя их «свободные» воли для того, чтобы воплотиться, осознать самого себя и самореализоваться.

* * *

Прежде всего, дадим определение финальности и финализму. Этого определения нет ни в БСЭ, где финальность отождествляется с телеологией, ни в каких-либо других авторитетных источниках, исключая [19]. Определим финальность как свойство развивающейся или эволюционирующей системы, заключающееся в предопределенном стремлении этой системы к достижению некоторой цели.

А финализм (в контексте универсальной истории) – как такое течение научной мысли, такой взгляд на эволюцию, который предполагает поэтапное движение мира от ее начала, точки «Альфа» (Большого взрыва), к предопределенному концу, финалу – точке «Омега». Подчеркнем, что речь здесь идет об универсальной (стартовавшей в момент Большого взрыва), а не только биологической эволюции.

Теория, гипотеза считается финалистской, если удовлетворяет хотя бы одному из следующих критериев [19]:

A. Примату целевых нематериальных отношений над реальными каузальными связями.

B. Наличию внутренней, наперед заданной программы развития, детерминирующей строгую направленность эволюции.

C. Уподобление эволюции онтогенезу и движению к неизбежному финалу.

D. Эквифинальность развития.

Здесь мы попытаемся показать, что финализм позволяет:

1. Объяснить парадоксы эволюции.

2. Понять выделенность современного ее этапа.

3. Объяснить феномен гиперболического роста населения Земли.

4. Понять причину ускорения эволюционного и исторического процесса.

5. Объяснить причину цикличности экономического и исторического развития.

6. Установить связь между аномальным поведением Солнца в конце XX – начале XXI столетия и явлением мирового демографического перехода, природа которой остается непонятной.

7. Объяснить парадокс молчания Вселенной.

8. По новому подойти к проблеме SETI и выработать оптимальную стратегию поиска внеземных цивилизаций.

Но сначала сформулируем принцип отказа от применения понятия бесконечность в естественных науках в тех случаях, когда при описании какого-либо явления или процесса невозможно указать его границы или количественную меру. Этот отказ не касается тех случаев, когда бесконечность как математическая абстракция используется в идеализированных теоретических построениях.

Без такого отказа невозможен переход к финалистскому описанию эволюции, т. к. финализм предполагает конечное, ограниченное количество «ресурсов», необходимых для ее реализации. Под ресурсами здесь понимаются не только материальные ресурсы: масса, энергия, число элементарных частиц… но также пространство и время.

Финитность – необходимое условие финальности. Природа не терпит бесконечности

Идеальные бесконечно удаленные элементы приносят лишь ту пользу, что делают систему законов и знаний возможно более простой и обозримой.

Давид Гильберт

Введение

Что такое финитность? Финитность в естествознании – это конечность, ограниченность в пространстве или во времени предметов, процессов, явлений. В философском смысле термин финитность подразумевает также временность и преходящесть всего сущего.

Финитизм (лат. finitus – определенный, законченный) – философское учение, отрицающее понятие бесконечности и утверждающее, что бесконечному нет места ни во Вселенной, ни в микромире, ни в человеческом мышлении. Было популярно в древнем мире и в средние века до Коперника. О финитности (и о финальности) исторического процесса пишет Николай Бердяев в книге «Философия свободы»:

«История не может иметь смысла, если она никогда не окончится, если не будет конца; смысл истории и есть движение к концу, к завершению, к исходу».

В текущем столетии разными авторами прогнозируется завершение роста численности населения Земли, конец экономического роста, конец науки, конец творчества, конец роста энергопотребления… Какие-то прогнозы верны – какие-то нет, но, очевидно, что представление о финитности и о финальности, т. е. о конечности социальных процессов, их устремленности к финалу, возможно промежуточному, является весьма востребованным в нашу переходную эпоху.

Насколько естественно использование понятия бесконечность в абстрактных математических построениях, настолько оно недопустимо при описании реально существующих материальных объектов и систем: такой подход никогда не приносит плодов и приводит лишь к заблуждениям. Выдающиеся и даже великие ученые приходили к ошибочным заключениям, допуская математическую бесконечность к описанию реальности.

Понятие бесконечность, которому не должно быть места в реальном мире, попадает в ментальный мир человека, во-первых, из религиозных представлений. Во-вторых, из философских теорий как идеалистических, так и материалистических. И, наконец, третий канал, по которому это деструктивное (при описании объективной реальности) понятие может проникнуть в сознание человека, – это математика.

Качественная бесконечность в идеалистической и материалистической философии

Вероятно, первым, кто ввел представление о бесконечности мира был древнегреческий философ Анаксимандр (VI в. до н. э.). Вселенная, по Анаксимандру, развивается сама по себе без вмешательства олимпийских богов. Источником происхождения всего сущего Анаксимандр считал некое бесконечное, «нестареющее» божественное начало – апейрон, которому присуще непрерывное движение. Сам апейрон, как то, из чего всё возникает и во что всё превращается, есть нечто сущее, постоянно пребывающее и неуничтожимое, беспредельное в пространстве и бесконечное во времени.

Иммануил Кант в своем знаменитом трактате по физической космологии «Всеобщая естественная история и теория неба» приходит к заключению о бесконечности Вселенной:

«Очевидно, что и она (Вселенная) не должна иметь никаких пределов… только так её можно соотнести с всесилием Бесконечного. Абсурдно было бы полагать, что Божество станет задействовать бесконечно малую часть своего могущества…» «…»

«Наименование «бесконечность» прекрасно и, собственно говоря, эстетично. Выход за пределы всех понятий о числе волнует душу и, смущая ее, приводит в изумление».

К такому же выводу, основанному на всемогуществе Творца, приходит в своей «Монадологии» и Лейбниц:

«Я в такой мере стою за актуальную бесконечность, что не только не допускаю, что природа боится ее, как обыкновенно выражаются, но и признаю, что природа всюду являет именно такую бесконечность, чтобы лучше отметить совершенство своего Творца».

Если бесконечность Канта и Лейбница является априорной, субъективной и трансцендентальной, то Гегель в своем труде «Наука логики» различает две бесконечности: «дурную», как простое отрицание конечного, и истинную бесконечность. Дурную бесконечность он описывает как «бессмысленное повторение», «скучное чередование», «повторяющуюся одинаковость».