Расчёт арбитражных ситуаций (вилок) в букмекерских конторах и на биржах ставок.

1/K1+1/K2 < 1

то, подставив в это формулу выражения BACK коэффициентов через LAY коэффициенты, получим условие вилочности на LAY коэффициенты:

1/(1+1/(KLAY1-1))+1/(1+1/(KLAY2-1)) = (KLAY1-1)/KLAY1+(KLAY2-1)/KLAY2=

2-(1/KLAY1+1/KLAY2) < 1

или

(1/KLAY1+1/KLAY2) > 1

То есть условие вилочности на LAY коэффициенты по виду очень похоже на условие вилочности для BACK коэффициентов. Все также, только знак ‘меньше’ поменялся на знак ‘больше’.

Аналогично выводится трех-исходное условие вилочности для LAY коэффициентов. Только здесь нужно применить условия вилочности для двойных шансов (справа вместо 1 стоит 2):

1/(1+1/(KLAY1-1))+1/(1+1/(KLAY2-1))+1/(1+1/(KLAY2-1)) < 2

(KLAY1-1)/KLAY1+(KLAY2-1)/KLAY2 +(KLAY3-1)/KLAY3 < 2

1-1/KLAY1+1-1/KLAY2 +1-1/KLAY3 < 2

(1/KLAY1+1/KLAY2+1/KLAY3) > 1

Получим условие вилочности для двух-исходной вилки, где один из коэффициентов выражен в BACK-форме, а другой в LAY– форме.

1/(1+1/(KLAY1-1))+ 1/K2 = (KLAY1-1)/KLAY1 + 1/K2 = 1 -1/KLAY1 + 1/K2 < 1

Или 1/KLAY1 – 1/K2 > 1

Вторая проблема, возникающая при расчетах вилок на биржах ставок, это учет комиссионных биржи. Первый случай, который мы рассмотрим, это когда только один из исходов вилки находится на бирже. В этом случае, как легко видеть, для вычисления условий вилочности и процента вилки нужно вычесть из дохода игрока величину комиссии на прибыль с выигравшего исхода. Тогда доход игрока будет равен

K*V – (K-1)*V*m, где m – комиссия биржи.

Если это выражение переписать как

(K – (K-1)*m)*V, то видно, что для определения условий вилочности и процента вилки, можно просто взять, вместо исходного коэффициента выплаты K, скорректированный на величину комиссии коэффициент K – (K-1)*m. Комиссия берется не со всего дохода игрока, а только с его чистой прибыли (K-1)*V.

Теперь рассмотрим случай, когда два исхода в вилке 1-X-2 находятся на бирже и комиссия биржи берется с рынка в целом. То есть, поскольку только одна ставка может выиграть, а другая обязательно проиграет, то комиссия берется с ‘чистой’ прибыли игрока на данной бирже. Она равна разнице между прибылью по выигравшему исходу и сумой второй, проигранной ставки.

Выпишем условия прибыльности, учитывая комиссию рынка. Здесь ставки 2 и 3 находятся на бирже, которая берет комиссию.

K1*V1 > V

K2*V2 – m*((K2-1)*V2-V3) > V (ставка на бирже)

K3*V3 – m*((K3-1)*V3-V2) > V (ставка на той же бирже)

В случае, если выиграла вторая ставка, чистая прибыль будет равна разнице между прибылью второй ставка (K2-1)*V2 и проигранной ставкой V3. Комиссия биржи будет равна

m*((K2-1)*V2-V3), где m – процент комиссии.

Аналогично рассматривается случай выигрыша третьей ставки.

Для нахождения условий вилочности воспользуемся методом равной прибыли на все исходы.

K1*V1 = K2*V2 – m*((K2-1)*V2-V3) = K3*V3– m*((K3-1)*V3-V2)

Из последнего равенства следует:

V2*(K2-m*K2+m-m) = V3*( K3-m*K3+m-m)

V2*K2*(1-m) = V3*K3*(1-m)

V2*K2 = V3*K3

Далее,

K1*V1 = V2*(K2-m*(K2-1))+m*K2*V2/K3

K1*V1 = V2*(K2-m*(K2-1)+m*K2/K3)

V2 = K1*V1/(K2-m*(K2-1)+m*K2/K3)

аналогично

V3 = K1*V1/( K3-m*(K3-1)+m*K3/K2)

V = V1+V2+V3 = V1*(1+K1/( K2-m*(K2-1)+m*K2/K3)+K1/( K3-m*(K3-1)+m*K3/K2))

Отсюда условия вилочности:

1/K1+1/( K2-m*(K2-1)+m*K2/K3)+1/( K3-m*(K3-1)+m*K3/K2) < 1

То есть они совпадают с условиями вилочности для обычной вилки 1-X-2 без комиссии, если коэффициент

K2 = KO2-m*(KO2-1)+m*KO2/KO3

K3 = KO3-m*(KO3-1)+m*KO3/KO2

Где KO2, KO3 – коэффициенты без учета комиссии, то есть те коэффициенты, которые даются в таблицах коэффициентов биржи

Всего существует 20 различных вариантов уравнений прибыльности (см. Приложение 1 и 2). Для каждого из таких уравнений существует три варианта распределения двух ‘биржевых’ ставок среди всех трех ставок. Это уже дает 60 различных систем неравенств, которые потребуется решить, что вывести условия вилочности коэффициентов на биржах ставок, то есть в условиях, когда берется комиссия в целом с рынка. Если учесть необходимость вывода формул распределения сумм ставок при ‘перекосах’, то это делает отдельный вывод всех этих формул практически бессмысленным. Гораздо проще будет, в таком случае, пользоваться общими формулами для условий вилочности и сумм частичных ставок, выведенными в разделе Расчет вилок в букмекерских конторах.

12. Вилки как источник ставок с перевесом.

Вилки являются хорошим инструментом игрока сами по себе. Но у них есть еще одно полезное свойство. Они являются неплохим источником ставок с перевесом. А именно – среди ставок составляющих вилку хотя бы одна ставка является ставкой с перевесом над конторой.

Если Вы посмотрите на все ставки данной конторы или множества контор, то много ли Вы сможете сказать наверняка про количество ставок с перевесом? – я думаю практически ничего. А вот если мы рассмотрим все ставки, входящие вилки то мы можем высказать одно вполне обоснованное суждение – среди ставок входящих в вилки не меньше 33% составляют ставки с перевесом. Действительно рассмотрим истинные вероятности исходов матча:

P1 + PX + P2 = 1

Допустим, что все коэффициенты в вилке (K1, KX, K2) меньше коэффициентов соответствующих этим истинным вероятностям исходов спортивного события.

K1 <= 1/ P1

KX <= 1/ PX

K2 <= 1/ P2

Тогда, суммируя неравенства, получаем

1/K1 + 1/K2 + 1/K3 >= P1 + PX + P2 = 1

Что противоречит исходному предположению, что коэффициенты образуют вилку. Значит, хотя бы один из коэффициентов K1, KX или K2 будет удовлетворять условию K > 1/P, то есть являться ставкой с перевесом.

Понятно, что если рассматривать только двух-исходовые вилки, то процент ставок с перевесом среди них будет не меньше 50%. Неплохая исходная позиция для реального практического поиска ставок с перевесом.

Существует простая стратегия, дающая гарантированный выигрыш в среднем за большой период – ставить случайным образом на один из исходов вилки. Доказательство выигрышности этой стратегии очень простое, хотя и не совсем строгое. Возьмем двух игроков. Один будет делать ставки из тех, что входят в состав вилки, совершенно случайным образом. А второй будет делать каждый раз ставку противоположную, той которую сделал первый игрок. Ясно, что ставки сделанные вторым игроком тоже ‘случайны’. То есть, математическое ожидание выигрыша у обоих игроков должно быть одинаковым. Пусть оно будет равно W. Но вместе они выигрывают 2*W. Поскольку, фактически каждый раз вместе оба игрока ‘проводят’ вилку, то 2*W > 0 и W > 0, то есть стратегия случайного отбора ставки в вилке – выигрышная в среднем стратегия.

Для практического использования алгоритм следует уточнить. Сумма ставки – постоянный возможный выигрыш (флет), или случайна, в каком-то диапазоне. Существует большая вероятность, что для плеча вилки, имеющего реальный перевес, контора быстро урежет максимум суммы ставки до величины ниже, чем предполагаемая сумма ставки. Если это не учитывать, то возникнет асимметрия, которая сделает алгоритм неприемлемым. Для восстановления симметрии применяем следующее правило. Перед тем как делать ставку на выбранное случайное плечо, проверяем также и противоположное плечо. На тот предмет, что там можно сделать ставку по той сумме, которую Вы заранее определили. То есть, что максимум не урезан. Если максимум урезан хотя бы в одном из плеч вилки, то ставка не делается вообще.

Применяя метод 'случайного плеча вилки', Вы можете иметь представление о величине Вашего перевеса. Как следует из доказательства его 'прибыльности', величина перевеса случайного плеча вилки будет равна величине прибыльности вилки, из которой выбирается случайное плечо. Для того, чтобы в этом убедиться  достаточно в предыдущем доказательстве выбирать случайно ставки но не из всего множества вилок, а из множества вилок с определенной прибыльностью.

А значит можно вполне обоснованно применить какой-нибудь вариант критерия Келли, который для увеличения скорости прироста банка ставит сумму ставки в зависимость от Вашего перевеса.

Дальнейшие изыскания могут быть в направлении дополнительной фильтрации вилочных исходов, с тем, чтобы повысить процент ставок с перевесом в отфильтрованном множестве. Например, часто в трех-исходной вилке два исхода находятся в одной конторе, а третий в другой. На мой взгляд, в такой ситуации более вероятно, что ставка с перевесом не будет среди тех двух, что находятся в одной и той же конторе.

Весьма правдоподобным будет предположение, что плечо с перевесом будет c меньшей вероятностью достигаться на линиях, которые предлагаются несколькими конторами одновременно. Так как маловероятно, что несколько контор сразу сдвинули линии настолько, что смогла образоваться ставка с перевесом. Но это все только предположения.

13. Неполные вилки.

Некоторые игроки, авторы статей по теории ставок на спорт и стратегий ставок (Geoffry, Ботин С), рассматривают так называемые неполные вилки. Берутся ситуации, когда коэффициенты выбранных исходов не образуют нормальной вилки. Но один из исходов

недооценен букмекерской конторой

то есть, по мнению игрока, должен иметь гораздо больший коэффициент.

Заниженный коэффициент часто бывает на ничью, чья вероятность, по мнению игрока, должна быть намного меньше, чем вероятность, вычисленная в соответствии с коэффициентом конторы. Если поставить на все исходы кроме ничьей и пренебречь вероятностью ничьей, то может получиться так называемая неполная вилка. В том случае, если оставшиеся исходы образуют реальную вилку (уже двух-исходную).

На эту ситуацию можно взглянуть и с другой стороны. Можно рассматривать ее как valuebet на две и более ставки. Действительно, обычно valuebet это ставка на исход с завышенным, по мнению игрока, коэффициентом. На него имеется смысл ставить, так как коэффициент выплаты больше, чем должен быть, будучи вычисленным по истинной вероятности исхода (которую имеет в виду игрок). Однако иногда бывает легче увидеть не завышенный, а заниженный коэффициент. В случае 3-х исходов коэффициенты на два остающихся исхода могут быть завышены. А могут и не быть завышены, если понижение исходного коэффициента произошло в основном за счет маржи. Может быть завышен, например, только один коэффициент.

Так как ставить в том случае если Вы решили поставить на два остающихся исхода? Автор идеи неполной вилки предлагает ставить на два остающихся исхода, если они образуют вилку – так называемую ‘неполную’. Но поскольку игра все же может закончиться, например, ничьей (третий, неучтенный исход – и при этом денежки пропадут), то эта ‘вилка’, в отличие от нормальной вилки, ничего не гарантирует. Нетрудно показать, что для того чтобы неполная вилка давала в среднем выигрыш, необходимо чтобы процент прибыльности ‘неполной’ вилки был непросто положительным, но и превышал истинную вероятность исключенного исхода. Если же все это записать в терминах коэффициентов, то это означает следующее. Для того чтобы ‘неполная’ вилка давала в среднем (потому что иногда будет проигрывать) выигрыш необходимо, чтобы исходный, заниженный (для неиспользованного Вами исхода) коэффициент, будучи скорректированным к более реальному, чем у конторы значению, тоже давал, вместе с оставшимися коэффициентами, обычную нормальную вилку.

В самом деле, допустим, что мы имеем неполную вилку на 2-исхода:

L = 1/K1 + 1/K2 < 1,

Обозначим как P3 вероятность третьего исхода, который не вошел в вилку. Тогда мы будем с вероятностью (1-P3) выигрывать на двух-исходовой вилке сумму V*(1/L-1) и с вероятностью P3 проигрывать сумму ставки V. То есть в среднем мы будем иметь:

(1-P3)* V*(1/L-1)– P3* V

Для того чтобы это выражение было положительным, необходимо чтобы:

(1-P3)*(1/L-1)– P3 > 0

или

1/L-1-P3 /L > 0

или

L+P3 < 1

или

1/K1 + 1/K2 + 1/K3 < 1

что и требовалось доказать.

Таким образом, чтобы гарантировать ‘чистоту’ неполной вилки, вы должны вычислить минимальный коэффициент 3-го исхода по коэффициентам двух первых исходов как

K3 = 1/(1– 1/K1 – 1/K2), вычислить максимально допустимую вероятность третьего исхода как P3 = 1/K3 и ответить для себя на вопрос: “Считаете ли Вы, что вероятность третьего исхода не выше этой вероятности P3”. Если Вы все еще даете ответ ДА на этот вопрос, то можете делать ставку на неполную вилку. Но может Вы уже засомневались, увидев реально вычисленную вероятность для реальной ставки? – все зависит от конкретной ситуации.

Теперь покажем, что неполная вилка 1-X-2 существует практически ВСЕГДА даже на линиях одной конторы. Действительно, допустим, что вилки нет ни на одной из трех возможных пар коэффициентов, то есть:

1/K1 + 1/K2 >= 1

1/K1 + 1/K3 >= 1

1/K2 + 1/K3 >= 1

Складывая эти три неравенства, получаем:

2*(1/K1 + 1/K2 + 1/K3)>= 3

или

1/K1 + 1/K2 + 1/K3 >= 1.5

Отсюда видно, что если это коэффициенты одной конторы, то маржа ее составляет более 50%, что практически исключено. И, значит, что если маржа конторы на линии 1-X-2 менее 50%, то одна из пар 1-2, 1-X или 2-X обязательно образует неполную вилку. Даже на линиях одной конторы. Для практических целей надо искать неполные вилки с максимальным процентом, комбинируя линии всех контор.

Рассмотрим различные варианты неполных вилок на линии 1-X-2 одной конторы и условия их существования.

1 вариант – одна неполная вилка.

1/K1 + 1/K2 >= 1

1/K1 + 1/K3 >= 1

1/K2 + 1/K3 < 1

То есть, пусть у нас есть одна неполная вилка, для определенности на коэффициентах 1/K2 и 1/K3. Сложим первые два неравенства:

2/K1 + 1/K2 + 1/K3 >= 2

И теперь применим третье неравенство:

2/ K1 + 1 > 2/K1 + 1/K2 + 1/K3 >= 2

Отсюда следует 2/K1 > 1 или K1 < 2

Это означает, что если какой-либо коэффициент из линии 1-X-2 в одной и той же конторе больше либо равен 2, то неполная вилка на оставшихся коэффициентах быть не может.

2 вариант – две неполных вилки.

1/K1 + 1/K2 < 1

1/K1 + 1/K3 < 1

1/K2 + 1/K3 >= 1

Сложим первые два неравенства:

2/K1 + 1/K2 + 1/K3 < 2

И теперь применим третье неравенство:

1 +2/K1 =< 2/K1 + 1/K2 + 1/K3 < 2

Отсюда следует 2/K1 < 1 или K1 > 2

До сих пор речь шла о классической вилке 1-X-2, но можно рассмотреть неполные вилки и для более сложных вариантов. Например, F1(0)-X-2. Если неполную вилку сделать путем выкидывания ничьей, то мы получим почти рассмотренный вариант, но не совсем. Он отличается тем, что при ничьей мы кроме проигрыша ставки 2, получаем возврат ставки 1. Это приведет к тому, что условие на ‘критическое’ значение коэффициента K3 будет слабее.

Но вот если считать, что заниженный коэффициент дается на 2, то есть неполная вилка будет, может быть образована событиями F1(0) и X, то получаем интересный вариант. Дело в том, что для событий F1(0) и X вилка существует ВСЕГДА. То есть, всегда можно подобрать V1 и V2, так что мы не проиграем, в случае если реализуется F1(0) или X. В самом деле, условия прибыльности для двух первых исходов:

K1*V1 > V

KX*VX+V1 > V

Если мы возьмем V1 = KX/( K1 -1)*VX, то оба неравенства удовлетворятся при любых K1 > 1 и KX> 1, то есть всегда. Вы это легко докажете сами. Но не спешите бежать и делать ставки, ведь есть еще и третий исход, 2. Для того, чтобы сравнить Ваши оценки вероятности этого исхода с максимально допустимой вероятностью, которая еще гарантирует прибыльность ‘неполной’ вилки, нужно вычислять так. Условие вилочности на полную вилку:

1/K1 +1/K2 + (K1-1)/(KX*K1) = 1

Отсюда ‘критическое’ P2 = 1/K1 + (K1-1)/(KX*K1). Если Вы считаете, что вероятность исхода 2 меньше P2 , то можете смело делать ставки на F1(0) и X, разделив суммы ставок в соотношении V1 = KX/( K1 -1)*VX и какими бы ни были K1 и KX, всегда получите прибыль в среднем.

14. Вилки с использованием специальных предложений контор.

Часто букмекерские конторы с целью привлечь к себе игроков делают специальные предложения, когда Вам возвращают деньги (при определенном условии), если Вы проигрываете ставку – Cash Back. Наберите в Google : cash back bookmaker и получите несколько ресурсов, где они собраны.

Например, Вы делаете ставку на точный счет и в случае проигрыша, если игра закончилась со счетом 0:0, Вам возвращают деньги. Для того, чтобы воспользоваться этим специальным предложением предлагается сделать следующие ставки. Первая ставка – это ставка на какой-либо точный счет в той конторе, где Вам делают специальное предложение. О том, как выбрать этот точный счет, точнее ставку – чуть ниже. Вторая ставка – это ставка против этого счета на какой-либо бирже ставок, например, Betfair. Если у Вас уже есть вилка то, в общем-то, больше ничего делать не надо, но это нетипичный случай. В общем случае вилки на этих двух ставках не будет, и, делая только эти две ставки, Вы будете каждый раз немного проигрывать. Но мы добавим еще третью ставку, против счета 0:0, которую тоже можно поставить на бирже. Посмотрим, что это дает. Если матч окончился со счетом отличным от 0:0, и отличным от счета, на который Вы поставили в букмекерской конторе со специальным предложением, то Вы получаете выигрыш по ставке против счета 0:0 по третьей ставке (на второй бирже), и выигрыш по ставке против точного счета по второй ставке (на первой бирже). Если матч окончился с точным счетом, по первой ставке, то Вы получаете выигрыш по первой ставке. И, наконец, если матч окончился со счетом 0:0, то Вы получаете выигрыш по второй ставке (на первой бирже) и возврат в букмекерской конторе, согласно их любезному предложению. Рассмотрим, при каких условиях на коэффициенты указанных выше событий мы получим прибыль при любом исходе игры. Только номера второй и третьей ставок поменяем местами.

Пусть K1 – коэффициент первой ставки на точный счет S в букмекерской конторе со специальным предложением, K3 – коэффициент против этого точного счета бирже (здесь мы рассматриваем его в форме BACK, то есть необходимо пересчитать его из LAY формата). И пусть K2 – коэффициент против счета 0:0 на второй бирже. Понятно, что первая и вторая биржа могут совпадать.

Напишем условия прибыльности наших ставок.

Счет не S и не 0:0.

Наш доход равен K2*V2 + K3*V3 > V

Счет S, то есть не 0:0.

Наш доход равен K1*V1+K2*V2 > V

Счет равен 0:0.

Наш доход равен V1+ K3*V3 > V

Ели мы посмотрим в приложении 1 на таблицу формул прибыльности вилок, то увидим, что наши формулы прибыльности совпадают с формулами прибыльности варианта вилки N 19. Соответственно можно брать и все остальные формулы, относящиеся к этому варианту вилочной ситуации. Формулы, которые касаются сумм ставок и вариантов перекосов. Такие же формулы применимы, например, к вилке типа F1(0)-12-2X.

На эту же ситуацию можно посмотреть и без учета третьей ставки против счета 0:0. Фактически ‘специальное предложение’ эквивалентно увеличению коэффициента ставки на величину (в процентах), равную вероятности нулевого счета. То есть, если вероятность нулевой ничьей равна 10% (~величина обратная коэффициенту), а коэффициент на выбранный Вами счет равен 12, то в среднем Вам повысили коэффициент до 13.2. Конечно, если Вы выигрываете, то получаете по коэффициенту 12. Коэффициент 13.2 будет только в среднем, то есть, если Вы будете часто делать подобную ставку. Если Вы будете комбинировать этот повышенный средний коэффициент с коэффициентом на противоположный исход (в данном случае LAY против этого точного счета на бирже), то можете получить статистическую вилку – то есть вилку, где вместо 12 Вы будете учитывать 13.2 и будет теоретическая вилка.

На каждой такой 'вилке' выиграть нельзя, но при долгой игре у Вас будет выигрыш. Реально будет так, что Вы почти все время будете проигрывать небольшую сумму, так как поставили на оба исхода, а они не дали реальную вилку, то есть дали отрицательную вилку (как говорят, те кто пользуется такими вилками для отыгрыша бонусов). Но иногда Вам будут возвращать одну из ставок, и это будет с лихвой компенсировать те небольшие

прошлые проигрыши. Но это только в случае если есть вилка с 'повышенным' коэффициентом. В нашем примере отрицательная вилка с 'фактическим' коэффициентом

должна быть не ниже чем вероятность нулевой ничьей. То есть при вероятности нулевой ничьей 10%, то Вы можете использовать все отрицательные вилки от -10% до 0 (ну и конечно выше – то есть обычные вилки). Если отрицательная вилка с фактическим коэффициентом имеет 'профит' -4%, то Ваш средний выигрыш будет 10%-4% = 6%.

Другие случаи специальных предложений рассматриваются аналогичным образом.

15. Вычисление коэффициентов на исходы с форами с использованием вилочных формул

Все условия вилочности построены таким образом, что если взять коэффициенты, участвующие в вилке без учета маржи в одной и той же конторе, то неравенство в условии вилочности превращается в равенство. Это свойство арбитражной ситуации было названо условием ‘эффективности’ вилочной ситуации. Оно дает возможность вычислять одни коэффициенты на основе других. Например, возьмем вилку:

F1(+1)-2-F2(-1.5) (коэффициенты будут иметь индексы 1-2-3)

Условие вилочности для нее имеет вид:

1/ K1+1/(K1*K3)+( K1-1)/(K1*K2) < 1

Коэффициенты без маржи, вычисленные в одной и тоже конторе, должны удовлетворять равенству:

1/ K1+1/(K1*K3)+( K1-1)/(K1*K2) = 1

Отсюда, например, следует, что, зная коэффициенты на исходы F1(+1) и 2, мы можем вычислить коэффициенты на исход F2(-1.5)

K3 = K2/((K2-1)*( K1-1))

Аналогично, взяв любую из списка вилок в приложении, мы можем использовать ее условие вилочности для вычисления любого коэффициента вилки по двум другим коэффициентам, участвующим в условии арбитражной ситуации.

16. Неэффективные арбитражные ситуации (вилки).

Здесь приводятся примеры арбитражных ситуаций, которые не удовлетворяют условию эффективности. Они тоже могут фактически реализоваться в жизни, но причиной их существования с большей вероятностью будет ошибка букмекерской конторы при публикации линий.

F1(-0.25)-2X

F1(-0.75)-2X

F1(-0.75)-F2(+0.25)

F1(-0.25)-F2(+0.75)

F1(-0.75)-X-2

F1(-0.75)-X– F2(-0.75)

F1(-0.25)-X– F2(-0.75)

F1(0)-2X– F2(-0.75)

F1(0)-F2(+0.75)-2

F1(+1)-2-F2(-1.75)

F1(+1)-F2(-0.25)-F2(-1.5)

F1(+2)-F2(-1.5)– F2(-2.75)

F1(+2)-F2(-1.25)– F2(-2.5)

F1(-1)-F2(+1.5)– F2(+0.25)

F1(-1)-F2(+1.75)-2X

F1(-2)-F2(+2.5)-F2(+1.25)

F1(-2)-F2(+2.75)-F2(+1.5)

17. Сервис сравнения линий

www.LiveLines.RU

и примеры вилок.

Сервис сравнения линий LiveLines.RU был создан в 2004 году. Сервис позволяет сравнивать линии более чем 80 букмекерских контор по играм более чем 200 спортивных лиг и находить лучшие коэффициенты выплат на нужные Вам игры. Кроме того, он находит арбитражные ситуации (вилки) и осуществляет их рассылку по email. Сервис работает в автоматическом режиме, непрерывно 24 часа в сутки. Ежедневно серверы линий сервиса собирают несколько гигабайт информации, обрабатывают их и рассылают несколько сотен мегабайт информации на основной сайт сервиса и зеркала сервиса. Количество найденных вилок варьируется от 5000 до 30-40 тысяч ежедневно. Количество игр – от 500 до 1500.

Ниже приводятся примеры вилок каждого типа и подробными объяснениями. Примеры взяты с сервиса LiveLines.RU.

Классические вилки.

Вилки 1-X-2 (формула 2).

Здесь мы возьмем вилку на матч Espanyol против Austria Vienna. Общая сумма ставки в 1000 рублей делится таким образом.

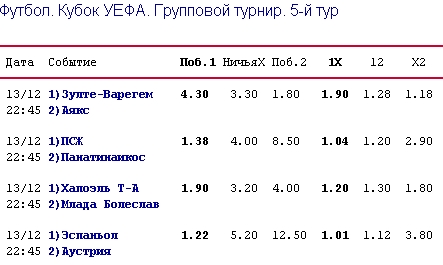
В Марафоне ставим 82.8 рубля на победу Austria Vienna и 198.9 рублей на ничью. Согласно коэффициентам выплаты мы получим, при ничьей 1034.28 рубля, при победе Austria Viena – 1035 рублей. То есть пока в выигрыше при любом варианте.

Осталось поставить на Espanyol в WagerWeb сумму 718.3. Коэффициент -225 а американском формате равен ~ 1.44 в европейском. При выигрыше Espanyol мы получим около 1034.35 рублей.