Трилогия ума: Научите ребенка думать по-новому. Восхождение от рассудочного мышления к разуму и мудрости

Учитель объясняет, что в то время, когда Земля вращается вокруг своей оси, она поворачивается к Солнцу разной стороной. Посмотрите, показывает на прибор учитель и скажите: в тот момент, когда Солнце освещает одну половину Земли, какое там время суток? (день). – А какое время суток на той половине, которая находится в тени, и не освещена Солнцем? (ночь). Может ли Солнце, задает новый вопрос учитель, осветить Землю сразу со всех сторон? Нет, отвечают дети.

Учитель объясняет, что такое год – это то время, за какое Земля облетает один раз вокруг Солнца. Он длится 365 дней. Далее объясняет, что год делится на четыре ортогональных сезона и называет их: зима, весна, лето, осень. Объясняет, что такое месяц и сколько месяцев в году (12). Просит детей их назвать. Объясняет, что такое сутки – это время, за которое Земля совершает один полный оборот вокруг своей оси (за 24 часа). Как нечто целое сутки, опять-таки, делятся на четыре одинаковые по времени части. И все это учитель связывает с понятием «ортогональное» Гераклита для того, чтобы эту систему ритмов приложить к другим природным и социальным системам.

По этой теме также можно организовать игру «Назовите слова, ортогональные по значению». Учитель говорит: «День и Ночь». Ученики называют слова, ортогональные по значению: «Вечер и Утро». Учитель называет: «Зима и Лето» – ученики называют: «Весна и Осень».

Выходит, что зима, весна, лето и осень, так же как и ночь, утро, день и вечер связаны не только противоположными, но и более сложными ортогональными отношениями. Учитель просит кого-либо из учеников нарисовать Ортогональное Гераклита, и вписать в эту геометрическую модель времена года. То же самое учитель предлагает проделать детям и со временами суток. Дети должны четко знать, что день и ночь по отношению к утру и вечеру ортогональны, также как зима и лето ортогональны по отношению к весне и осени. Для демонстрации этой мысли, учитель вычерчивает на доске соотношение двух ритмов: суточного и сезонного.

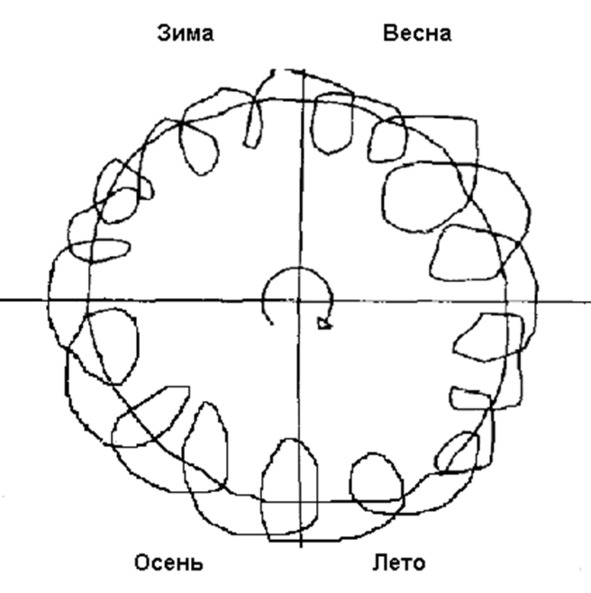
Рис. 5. Участие земли в суточных и сезонных ритмах

В старших классах, дети должны учиться понимать, что ортогональными отношениями связаны между собой север и юг с востоком и западом, потенциальная с кинетической энергией, электрическая энергия – с магнитной энергией. То же самое касается и общественных процессов, в которых рабовладельческая общественно-экономическая формация с ее противоположными классами рабов и рабовладельцев ортогональна по отношению к феодальной формации с преобладающими в ней классами феодалов и крепостных. В таком же ортогональном отношении находится старшее и младшее поколения людей, в котором папа и мама оказываются ортогональными по отношению к сыну и дочери.

Выходит, что «отцы и дети» – это не противоположные друг к другу понятия, как принято многими считать, а ортогональные. Поэтому все круговые, циклические движения во многих случаях лучше всего объяснять не при помощи пифагорейской, а при помощи гераклитовской модели, отражающей в разумном мышлении все формы обмена ресурсами. Эта же мыслительная структура напрямую касается и «клеточки» буржуазного общества, которую Карл Маркс положил в основу своего фундаментального труда «Капитал», в котором стремился переосмыслить и изменить современное ему общество с позиций разумного мышления. И совсем другое дело, удалось ли ему это.

Спрашивается, разделил ли Маркс рассудок и разум в своих трудах, как это мы проделали в представляемой читателю работе. К сожалению, не разделил. Не отделил он и мудрость от двух предшествующих ступеней в развитии ума, хотя был чрезвычайно близок к этому. В. И. Ленин, один из выдающихся вождей пролетариата где-то в своих многочисленных работах отметил: «Маркс не оставил Логики с большой буквы, но он оставил Логику «Капитала». И в этом отношении Ленин был прав. Я же скажу, что понять марксизм во всем его противоречивом многообразии, и особенно мышление самого К. Маркса можно не иначе, как овладев разумом и мудростью, как мышлением сравнительными понятиями, освоить которое мы и предлагаем в данной книге.

В методике формирования философских представлений, как мы уже видим, важное место занимает абстрагирование, т.е. движение от «вещей» к общим понятиям. Последние часто совпадают с геометрическими фигурами: прямоугольным треугольником, окружностью и т. д. А также, наоборот – от образа фигуры, от абстракции к реальным вещам и процессам. Это достигается систематическим использованием приёма материализации геометрических образов, которые зачастую адекватно отражают философские обобщения.

Не случайно при входе в Академию Платона было написано: «Да не войдет сюда тот, кто не знает геометрии».

Ибо геометрия – это не только раздел математики, это фундаментальный элемент философской культуры, помогающий отвлекаться учащимся от конкретных свойств материальных вещей и таким образом овладевать философскими и математическими (геометрическими) знаниями и представлениями. Осмыслив первоначала и научившись при помощи них думать, школьники с помощью задаваемых учителем вопросов самостоятельно будет находить их проявления в бесконечном многообразии окружающей реальности.

В итоге дети начнут осваивать проблемно-поисковый, исследовательский способ, получат то средство, которое обеспечит связное видение мира, т.е. метапредметное знание о природных и социальных процессах, чего не дают и не могут им дать все другие подходы и методы, имеющиеся в арсенале современного образования.

Используя в учебном процессе конкретно-научные и конкретно-всеобщие понятия: «противоречащее», «соотнесенное», «противоположное», «ортогональное» и другие, мы, таким образом, шаг за шагом накапливаем об окружающем мире общее знание. Мы по-новому начинаем понимать философию и, таким образом, вводим в школьное образование метапредмет, который совместно со старой рассудочной философией, арифметикой и геометрией будут синтезировать естественнонаучное и социально-гуманитарное знание. Ибо мышление сравнительными и математическими понятиями позволяет осмысливать с одинаковых для всех объективных точек зрения не только природу, но и общество.

Сопровождая курс арифметики, геометрии и физики, философия в современной школе добьется их единства и наглядности, что является необходимыми условиями их успешного изучения. При этом удачное и умелое применение наглядности побуждает детей к познавательной самостоятельности и повышает их интерес к предмету, является важнейшим условием успеха.

В тесной связи с наглядностью обучения находится и его практичность, поскольку именно из жизни черпается конкретный материал для формирования наглядных философских представлений. В этом случае обучение становится согласованным с жизнью ребенка.

Из сказанного выше следует, что основой формирования у детей представлений о конкретно-всеобщих сравнительных понятиях является способность к восприятию «одинакового в различном», и наоборот – «различного в одинаковом». Эта способность позволяет ребенку узнавать, отождествлять и различать, казалось бы, совершенно разные проявления реальности, закрепляя их в философских понятиях: тождественное и различное, соотнесенное и противоположное и т. д.

Цель метода наглядности в школе – обогащение и расширение непосредственного, чувственного опыта детей, который является условием для последующего перехода от разумного мышления к систематическому конкретно-всеобщему мышлению, т.е. к мудрости. Поэтому в начальных классах применяется естественная, рисунковая, звуковая и графическая наглядность. Затем эти методы применяются на всех этапах педагогического процесса. Их роль в том, чтобы дать опору для формирования в будущем устойчивого разумного мышления, отражающего объективные природные и социальные связи.

4. Философия как строгая школьная наука

В отличие от всех образовательных программ, как, видимо, стало понятно читателю, «Трилогия ума» Юрия Ротенфельда имеет задачу развивать мышление ребенка, начиная с детского сада до университетской скамьи. Но прежде, чем идти дальше, я вкратце вынужден повториться:

– наше мышление понятийно;

– язык состоит всего лишь из двух типов понятий: классификационных и сравнительных;

– сравнительные понятия делятся на конкретно-научные и конкретно-всеобщие (философские) понятия.

В конечном счете, речь у нас зашла о трех типах понятий: классификационных и двух типах сравнительных, использование которых в мышлении дает три четко разграниченные ступени в развитии ума: рассудок, разум и мудрость.

– Рассудок (рассудочное мышление) определяется использованием классификационных понятий.

– Разум (разумное мышление) помимо классификационных понятий использует конкретно-научные сравнительные понятия разных видов, числа и другие математические абстракции.

– Мудрость (философское мышление) возвышается над рассудочным и разумным мышлением благодаря тому, что использует конкретно-всеобщие сравнительные понятия, собранные в кумулятивный ряд, дающий кумулятивную панлогическую картину мира5.

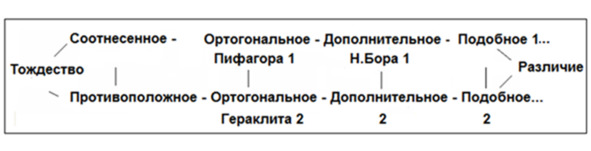
Схема 4. Декалог – кумулятивная панлогическая картина мира

По мере взросления детей и перехода их из класса в класс, т.е. по мере познания ими окружающей действительности, мы выстраиваем школьное знание в два параллельных ряда конкретно-всеобщих сравнительных понятий, каждое из которых дает объективную точку зрения на природный и социальный мир.

Причем все составляющие этот ряд понятия, ставятся одно за другим, не как попало, а в определенном строго заданном порядке, отражающем переход от одинаковости сопоставляемых сторон, т.е. от их тождества к постепенно возрастающему различию. Существование этого ряда, шаг за шагом, позволяет собирать в голове ребенка расколотое по предметам и далее раздробленное на мельчайшие кусочки знание не по предметному принципу, как это имеет место во всех странах мира, а по межпредметному, панлогическому философскому принципу. Тогда как наполнение включенного в Декалог того или иного философского понятия конкретно-научным смыслом, можно посмотреть на примере понятия «соотнесенно». Таким же приемом можно проверять знание детей, извлекающих конкретно-научное содержание из любого конкретно-всеобщего понятия:

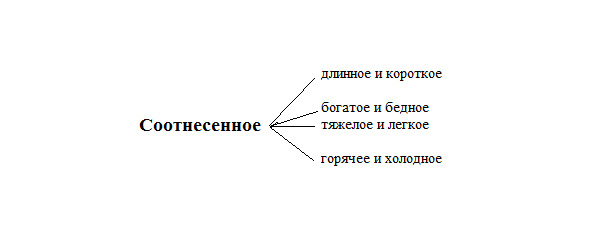
Схема 5. Наполнение общего понятия конкретно-научным содержанием

Продвижение по двум ветвям общего кумулятивного ряда к все более сложным понятиям приводит к обучению детей множеству частных и общих знаний. При этом ребенок должен понимать, что каждое менее сложное понятие кумулятивного ряда представляет собой частный случай (вырожденное состояние) более сложного понятия, например, «Соотнесенное» и «Противоположное» – это вырожденное состояние понятий «Ортогональное 1» Пифагора и «Ортогональное 2» Гераклита. Тогда как понятие «Тождественное» – это вырожденное состояние понятий «Соотнесенное» и «Противоположное».

Выходит, что «все познается в сравнении» и не иначе как относительно той или иной строго заданной, а, значит, одинаковой для всех объективной точки зрения. При этом точки на схемах обозначают множество не показанных сравнительных понятий (универсалий), каждое из которых приходится находить в той или иной сфере действительности и экстраполировать6 на весь мир.

Причем, если по математике в первом классе дети изучают числа и место каждого из них в общем ряду. После какого, и перед каким числом называют то или иное число при счете, то в курсе школьной философии имеет место то же самое, однако речь идет не о числах, а о конкретно-всеобщих сравнительных понятиях.

Так постепенно у детей формируется понимание того или иного сравнительного понятия, как того общего, универсального, что характеризует класс входящих в него конкретных отношений. Например, философское понятие «тождество», воплощающее собой «ноль» различия, выражает одинаковое в вещах. Тогда как понятие «различное», из которого шаг за шагом извлекают все сравнительные понятия, аналогично понятию «много».

Так постепенно дети убеждаются в том, что все сравнительные понятия строго упорядочены. После нулевой ступени – «Тождественное», расположена ступень, на которой находятся два понятия «Соотнесенное» и «Противоположное». При дальнейшем ранжировании понятий, на следующей ступени располагают «Ортогональное 1» Пифагора и «Ортогональное 2» Гераклита. На более высоких ступенях находятся понятия «Дополнительное», «Подобное» и «Порядковое», знакомство с которыми может начаться лишь после ознакомления школьников с изложенными К. Марксом законами. Прежде всего, это «закон соответствия производственных отношений характеру и уровню развития производительных сил», который наряду с физическим принципом дополнительности Нильса Бора, схватывает понятием «Дополнительное» похожесть неких социальных и физических структур. О более сложных сравнительных понятиях, отражающих более сложные структуры реальности, например, такой как «базис и надстройка», говорить пока не приходится.

По этой причине отношения между сравнительными понятиями и наполнение каждого из них смыслом раскрывается постепенно, по мере перехода от одних тем математики (а в старших классах, и физики) к другим. В результате дети начнут понимать, что разум расчленяет знание о мире на части, поскольку осмысливает реальность, используя в качестве начал множество конкретно-научных сравнительных понятий. Мудрость, напротив, собирает знание воедино – в научно обоснованную метапредметную картину мира, поскольку в качестве начал познания использует данные наших органов чувств, в конце концов, дающих сугубо научные конкретно-всеобщие сравнительные понятия.

Так изучая универсалии, мы шаг за шагом формируем структуру мышления обучаемых, которая включает в себя три логических направления, составляющих «Трилогию ума»:

– формальную логику, исходной мыслительной парадигмой которой является понятие «противоречащее». Его стороны выражают абстрактное, бесконечное различие, поэтому в Схемах 1, 2, 3, 4 они отстоят друг от друга на максимальном расстоянии. Это направление обусловливает возникновение классификационных понятий естественного языка, речи и рассудочного мышления;

– метафизическую логику конкретных наук, исходной парадигмой которых является понятие «Соотнесенное», на основе которого возникают числа, счет, арифметика и другие разделы математики;

– диалектическую логику, исходной парадигмой которой является понятие «Противоположное», понимаемое не иначе, как в аристотелевском смысле. То есть как «избыток» и «недостаток» того или иного субстрата относительно «промежуточного» положения.

Каждая логика определяется своим, только ей присущим началом, задающим объективную точку зрения для осмысления реальности. При этом рассудок разводит абстрактные различия А и не-А, не допуская их совмещения в одном и том же отношении: либо А, либо не-А, третьего не дано. Разум же, напротив, схватывает конкретные различия в единстве, поскольку одна сторона «соотнесенного» или «противоположного» как и других сравнительных понятий не может существовать без другой стороны.

Причем понятия верхнего и нижнего ряда кумулятивной парадигмы отражают две равнозначные ветви разумного мышления: конкретно-научное метафизическое разумное мышление (М) и конкретно-научное диалектическое разумное мышление (Д). Поэтому Ум представляет собой совокупность рассудка и двух форм разума:

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Примечания

1

Eric Grain – философ и педагог, интересующийся вопросами строгой философско-педагогической науки.

2

To quote from Kant’s lectures for 1765—66: «he is to learn, not thoughts, but thinking; he must be guided, not carried, if he is to be able to walk by himself later.» Цитата из лекций Канта за 1765—1766 гг.

3

Rotenfeld Yuriy. Trilogy of Intellect as a New Method of Children Intellectual Development, Philosophy Study, ISSN 2159—5313 January 2014, Vol. 4, No. 1, 36—40.

4

Выражение, которое употребляется в значении «с начала (и) до конца». Дословный перевод – «от яйца и до яблок».

5

Панлогизм – (от греч. pan – всё и logos – разум) – учение, согласно которому мир есть актуализация разума, логоса; иногда П. называют также учение о логической природе Вселенной.

6

Осуществлять экстраполяцию; распространять выводы, полученные из наблюдения над одной частью явления, на другую его часть или на всё явление в целом.