Гравитация и эфир

Мы можем так, на зло физикам, и далее плести эти последние кружева объяснений, хоть до посинения. Пока физики не поймут суть инерции движения любого тела. Школьники-то тут могут быть, пожалуй, более согласны здравому смыслу, чем физики – квантовомеханики.

Если же за нулевой уровень энергии для каждой данной стационарной орбиты принимать тот уровень энергии системы, вокруг которого происходят колебания энергии системы, то ту часть потенциальной энергии, которая расходуется в системе на удержание электрона на стационарном уровне, можно будет считать «энергией связи» электрона к уровню данной орбиты. И тогда кинетическая энергия движения электрона по орбите (как её положительное отклонение от энергии нулевого уровня орбиты) и энергия связи к уровню орбиты (как её отрицательное отклонение от энергии нулевого уровня) будут являться теми дисперсиями, колеблющими энергию вокруг математического ожидания – как среднего уровня энергии орбиты – уровня, приравненного к нулевому (рис. 21.6).

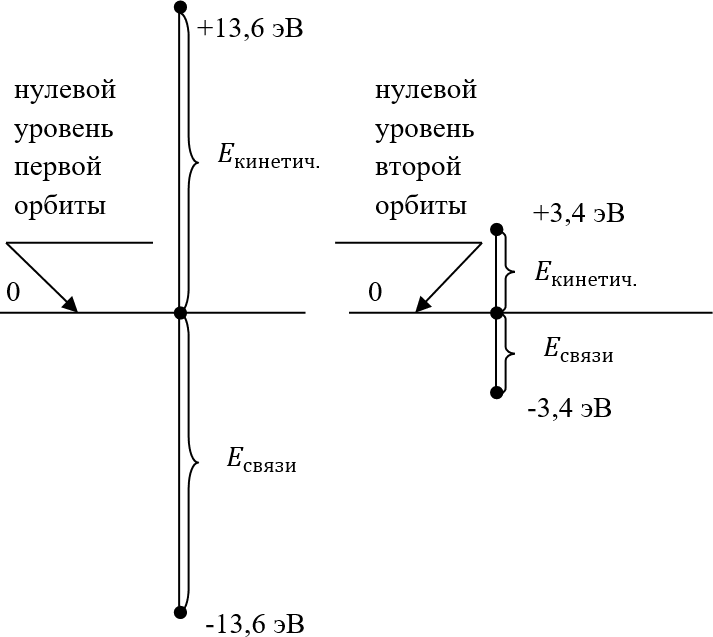
Рис. 21.6

Отсюда мы можем прозрачно увидеть самую суть «теоремы вириала». Какой бы ни была кинетическая энергия колеблющегося тела (у нас – электрона), но для того чтобы обеспечить стабильную амплитуду колебаний тела (у нас – стабильную стационарную орбиту электрона), оно должно быть привязано к некоторому данному равновесному уровню точно такой же энергией связи, с какой кинетической энергией тело колеблется. И наоборот: если тело привязано к какому-то уровню средней энергии колебательной системы, то для получения стабильных стационарных колебаний его кинетическая энергия должна в точности равняться энергии его привязки к системе. В любом из этих двух случаев комментирования одного и того же явления, общая энергия колеблющейся системы будет, следовательно, складываться из двух равных по модулю половинок энергий.

Рассмотрим теперь случай перевода электрона со второй орбиты на первую действием на электрон замедляющих квантов энергии. Здесь квант, налетающий из точки 2 (рис. 21.7) должен быть тормозящим положительным; квант из точки 3 – замедляющим отрицательным, отталкивающим электрон в сторону – противоположную источнику этого отрицательного кванта.

Сразу после замедляющего удара скорость электрона становится меньше орбитальной

. При многовитковом переходном процессе скорость электрона в конце перехода должна быть равной его скорости на первой орбите:

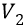
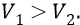
В течение всего переходного процесса электрон будет «медленно» набирать линейную скорость и кинетическую энергию, опускаясь по многовитковой спирали на орбиту 1.

На самом же деле многовитковый путь перехода электрона на первую орбиту будет ещё более замысловатым, допускающим начальную эллиптическую орбиту. Но в любом случае окончательное «причаливание» электрона к первой орбите случится по «почти окружности», переходящей на последних витках приближения к окружности первой орбиты.

Здесь мы обратим особое внимание школьника на то, что такой переход (2–1) может случиться так называемым «без излучательным» (типа 2S1–1S1). Для того чтобы переход был «без излучательным», электрон орбиты 2 надо затормозить лишь «чуть-чуть», то есть тормозящий квант энергии должен быть очень малым, значительно меньшим величины одного электронвольта. То есть его энергии должно хватить лишь на то, чтобы выбить электрон с «орбитальной подставки», какая действует для каждой конкретной стационарной орбиты, причём для каждой – своя по величине. О механизме «подставки» мы где-то упоминали в одной из глав второго тома Философии.

Диаграмма перевода электрона замедляющим квантом энергии со 2-ой орбиты на первую

Рис. 21.7.1

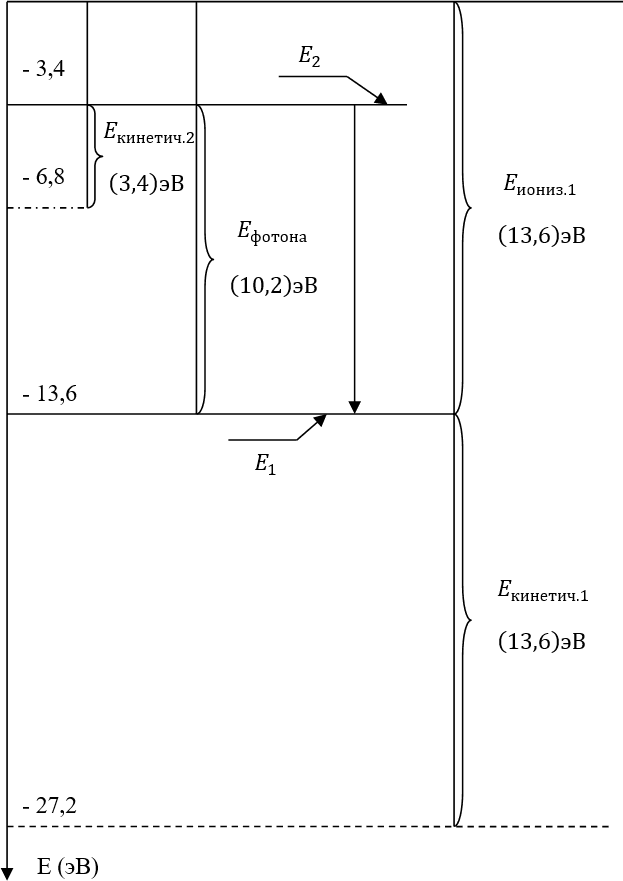
Рис. 21.7.2

Выбивание из «подставки» – это выбивание электрона из режима резонанса со всеми квантами-частицами поля протона, которые, делая свой полный оборот на радиус-луче между первой и второй орбитами, «причаливают» к очередной орбите (ко второй, в данном случае) точно «кольцо к кольцу» по пространственной фазе с конструкцией электрона, смотрящего в этот момент плоскостью своего кольца точно по радиус-лучу на протон. Нормальная расфазировка плоскостей электромагнитных колец конструкций электрона и кванта-частицы поля протона, характерная для механизма резонансной «подставки», должна находиться в пределах «плюс-минус

». При большей расфазировке взаимодействующие кольца-орбиты частиц разворачиваются настолько, что при пролёте «кольцо сквозь кольцо» конструкции не успевают обменяться той «резонансной» порцией энергии, которая в этом их резонансе «заметно» повернула бы в пространстве конструкцию каждой из взаимодействующих частиц. То есть за пределами одного градуса по расфазировке частицы перестают «видеть» друг друга, взаимодействуя слишком слабо для того, чтобы повернуть конструкцию электрона на очередную хорду его прямолинейных отрезков движения «по окружности» орбиты.

Мы утверждаем своей квантовой физикой о том, что на самом деле никаких «без излучательных» переходов в атоме не бывает. Даже в таком «плавном» переходе – с круговой орбиты 2S на круговую орбиту 1S (этот переход физики просто не видят), всё равно излучается соответствующий фотон. Но этот фотон наши физики не видят точно так же, как они же не видят мириады фотонов, излучаемых на самом деле каждым атомом даже в стационарном режиме его работы, с электроном стабильно вращающимся по любой стационарной орбите. Когда-нибудь физики научатся видеть такие фотоны. И начинать их видеть им легче всего будет сначала – именно с фотонов, излучаемых в «без излучательных» переходах.

В квантовой же механике физики называют «без излучательным» тот переход, когда атом сталкивается с другой частицей и теряет энергию на столкновение с ней или наоборот – приобретает энергию. В частности, к такого типа переходам они относят возбуждение атома электронным ударом. Правда, при этом физики умалчивают о том, почему в этих случаях переход получается без излучательным. Для них, если в результате перехода отсутствует фотон излучения, то значит переход – без излучательный. Но в любом таком случае орбитальный электрон всё равно переходит на другой уровень. И если он туда переходит, то фотон атомом обязан излучаться. Но физики просто не видят этот фотон. Более того, теория квантовой механики разрешает физикам не думать по поводу того, почему в этих случаях переход получается без излучательным.

Мы не будем и далее углубляться в физику «без излучательных» переходов. Школьник же, поняв истинную квантовую природу атома (классическую природу), сможет помочь профессионалам разобраться в гигантском разнообразии «без излучательных» переходов и в гигантском разнообразии тех фотонов, которые на самом деле излучаются атомом в этих переходах.

В атомной решётке какого-нибудь кристалла или металла «наблюдаются» многочисленные «незатухающие» эллиптические орбиты электронов многоэлектронных там атомов решётки. Но они не затухают лишь потому, что постоянно возбуждаются одними и теми же фотонами одних и тех же энергий, следующих для данной орбиты данного атома – с одних и тех же направлений от других (соседних и «далёких» атомов), возбуждаемых, в свою очередь, другими фотонами, излучёнными соседними или «далёкими» атомами. «Одни и те же фотоны» излучаются другими атомами и подлетают к данному с высокой степенью периодичности – лишь по причине жёсткой согласованности всех орбит всех атомов кристалла. Согласованность же приводит не только к высокой направленности излучаемых фотонов, но к высокой степени суммируемости этих фотонов, следующих в каком-то данном направлении сразу от суммы следующих друг за другом атомов решётки.

Разбираться в механике и энергетике всех этих согласованностей для каждого типа вещества – интереснейшая работа не столько для физиков и химиков, сколько для самих школьников, которые смогут запросто заменить профессионалов в этой «рутинной» для профессионалов работе. Надо только в школьных кабинетах развернуть соответствующий лабораторный стенд, оборудованный сравнительно недорогими приборами. В результате мы получим множество школьников, увлечённых физикой и химией ещё не выходя из школы. А некоторые из них будут влюблены в науку, даже самостоятельно программируя новые материалы, доселе невиданные человеком.

* * *

Теперь мы специально обратим внимание школьника на тот рубеж, на котором Нильс Бор отошёл от классического пути исследования атома в сторону чисто энергетического пути, где уже отсутствовали силы, орбиты и скорости электронов. Бор начинает свои выводы сначала с классики, а именно, – со сравнения сил, действующих на электрон на стационарной орбите. Он приравнивает центростремительную силу, действующую на орбитальный электрон (с точки зрения классической механики движения тела массой m по окружности), с силой Кулона, действующей на этот же электрон (с точки зрения электростатики):

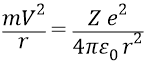
Полной энергией электрона (E) на круговой орбите является сумма его кинетической и потенциальной энергии (для «единичного» заряда Z=1):

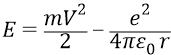
Но далее Бор уходит в своём выводе от кинетической энергии движения электрона, заменяя произведение содержащее кинетические параметры m и V (из первого выражения) на энергетические, то есть начинает работать только с энергиями:

И тогда

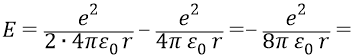
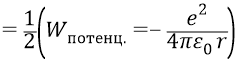
То есть полная энергия атомной системы у Бора оказывается равной половине отрицательного значения потенциальной энергии электрона (системы). Об этом же мы уже много говорили ранее, выше по тексту.

И далее Бор уже не говорит больше ни о каких «кинетических энергиях», а орбиты превращаются у него просто в «уровни энергии», то есть в «энергетические полочки», по которым электрон не движется – в соответствии с реальными в атоме законами механики и электродинамики, но скачет с орбиты на орбиту по новеньким законам только что родившейся механики – как чисто математически-энергетической теории, получившей название «квантовой механики».

Эта новая механика согласуется с опытом спектроскопических исследований физиков – «в первом приближении» (как мы выражаемся), хотя на первый взгляд это «приближение» выглядело тогда, в первой четверти 20-го века, довольно впечатляющим. Но только классика, которой мы здесь пытаемся заниматься, способна исследовать атом не «в первом приближении», но досконально точно, с точностями цифр, теряющимися во многих знаках после запятой.

Итак, классическая сфера поля положительного заряда в атоме на самом деле «стягивается» в тонкую окружность атомной орбиты. А это значит, что поле заряда (Е) распределяется теперь на любом радиусе удаления от заряда не по площади

, но по дуге-линии-орбите

. Поэтому формула для кулоновской силы должна бы в атоме трансформироваться, в соответствии с действительной физикой процесса, из её вида

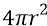
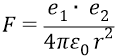
в вид

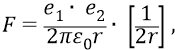
где напряжённость поля, действующего на заряд

(электрон) представляется в виде:

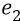
Но на самом деле, если мы возьмём пробный заряд

(электрон), поместим его на окружность орбиты, принадлежащую сфере, и измерим силу, с которой заряд притягивается к источнику поля

, то эта сила для данного атома будет какой-то конкретной (независимо от разных формул, пытающихся её интерпретировать по-своему). То есть левые части разных формул (с символом в них Е) безусловно совпадают по своему единственному (опытному) значению. Но вот с правыми частями формул предположения у нас с физиками – разные.

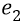
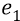
Ещё раз о напряжённости поля. Если в поле заряда

(протона) поместить заряд

(электрон), то напряжённость поля в точке заряда

определяется силой F, действующей на этот заряд

(на электрон). Эта напряжённость равна отношению силы к этому заряду

:

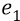
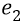
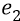
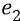
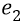
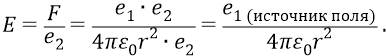
Далее, поскольку мы будем переходить к вычислениям, то, говоря о поле Е, будем иметь в виду единичный заряд протона и поэтому будем опускать значёк-наименование заряда (

) и использовать его обобщённое обозначение – е.

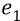
Итак, физики говорят, что закон изменения напряжённости при удалении от заряда-источника поля должен быть обратно пропорционален квадрату удалённости от заряда-источника:

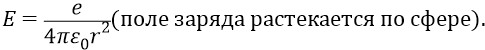
Но мы утверждаем, что закон изменения напряжённости обязан быть обратно пропорционален первой степени удалённости от заряда:

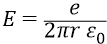
(поле заряда растекается по тонкой окружности орбиты).

Как примирить обе эти формулы при том, что они обязаны давать одинаковый результат в базовой «точке» – на окружности первой боровской орбиты? Ведь для этого базового режима работы атома разными физиками определены физические постоянные, подтверждённые опытом спектроскопистов.

Кроме того, если у физиков формула для Е даёт классическую размерность напряжённости – В/м, то в нашей желаемой формуле размерность явно искажена. Поэтому, для того чтобы всё же отстоять верный закон изменения напряжённости, соответствующий природе атомного резонанса, нам ничего не остаётся, как по форме оставить нашу формулу верного закона, но ввести в неё корректирующий коэффициент, уравнивающий эту формулу с формулой физиков:

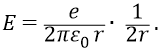
Здесь теперь соблюдена и размерность Е, и её величина. Однако мы не имеем права оставлять далее в формуле коэффициент

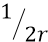
, но должны его: с одной стороны – учесть, с другой – убрать с глаз долой. И поэтому нам не остаётся ничего другого, как ввести в физику новую постоянную, которая будет называться не

– «электрическая постоянная»,

но

– «электрическая атомная постоянная».

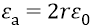
И тогда формула для закона напряжённости внутриатомного поля будет следующей:

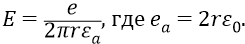
Проверим размерность напряжённости Е:

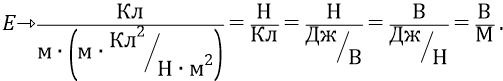
Здесь использовано фундаментальное определение потенциала

:

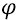
потенциал

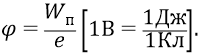
Вычислим теперь значение новой «атомной электрической постоянной» для фундаментальной «точки» поля – как для значения поля на уровне первой боровской орбиты:

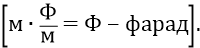
«Фарад» – это единица электрической ёмкости. Получается, что напряжённость поля Е, создаваемая зарядом

(протоном – ядром атома):

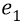
прямо пропорциональна этому заряду (что естественно и очевидно);

обратно пропорциональна первой степени (линейной) удалённости точки положения электрона от ядра (к чему мы стремились);

обратно пропорциональна электрической ёмкости между точкой (заряда-ядра) и окружностью той орбиты, на которой находится электрон на удалении

от ядра.

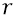
То есть чем больше ёмкость того местоположения, по которому может «растекаться» заряд (электрон на линии – дуге окружности), тем меньше напряжённость поля Е на этой дуге окружности. Всё соответствует физике электрических величин и электрических процессов внутри атома.

Ещё раз. Конструкцию атома можно представить в виде электрического конденсатора, состоящего из двух «обкладок». Первая обкладка – точечная; там на ней находится положительный заряд ядра атома (протон – как единичный положительный заряд

). Вторая обкладка «конденсатора» – это дуга-окружность атомной орбиты, куда «притёк» на эту обкладку заряд электрона

, равный по величине, но противоположный по знаку заряду ядра. Можно даже сказать, что поскольку на первой обкладке оказался положительный заряд, то на второй обкладке (на дуге окружности) «навёлся» такой же по величине, но отрицательный заряд в виде заряда единичного электрона.

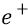
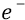
Электроёмкость в электростатике характеризует способность проводника (у нас – дуги окружности) накапливать заряд. Если бы на «проводник»-орбиту можно было бы поместить заряд 1 Кл, и этот заряд на дуге-окружности орбиты создал бы потенциал 1 В, то электроёмкость проводника («конденсатора»-орбиты) была бы равна 1 Ф (один фарад):

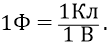
Вспомним ещё раз – что такое потенциал. Потенциалом точки (орбиты) электростатического поля называется отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду:

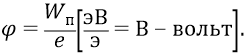
То есть потенциал равен той энергии

, которая была затрачена на перетаскивание (перемещение) заряда

 из бесконечности в данную точку (на орбиту). Деление этой энергии на заряд

– это просто нормировка затраченной энергии к величине «перетащенного» заряда (у нас заряд – единичный

).

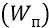
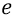
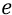
То есть когда мы перетаскиваем на орбиту заряд

, то этот заряд создаёт вокруг себя (вокруг «проводника»-орбиты) электрическое поле. И это поле обладает потенциалом, который можно измерить. Если мы на перетаскивание затратили энергию в «один электронвольт» (эВ), то поле будет обладать потенциалом в «один вольт»:

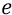
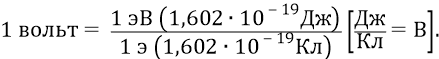
Так в электростатике определяется классически величина «один вольт». Если бы на эту же орбиту можно было бы поместить ещё один такой же заряд

, то поле этой орбиты обладало бы потенциалом

2 вольта.

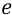
Ёмкость же «обкладки»-орбиты не зависит от величины заряда, размещаемого на обкладке:

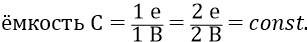
Ёмкость определяется только конструкцией «конденсатора» (атома) и размерами его обкладок (размерами орбиты). Так, первая боровская орбита обладает ёмкостью, которую мы уже вычисляли:

Ещё раз заметим, что если мы захотим на каком-то конденсаторе (на какой-то, допустим, проводящей сфере) разместить заряд 1 Кл, который может равномерно растекаться по этой сфере, и потребуем, чтобы потенциал поля этого конденсатора (этой сферы) составлял бы всего 1 вольт, то нам потребовалась бы сфера ёмкостью 1 фарад. Это – гигантская сфера, потому что, к примеру, сфера поверхности планеты Земля обладает ёмкостью всего лишь 708 мкФ (меньше одного миллифарада).

Когда же мы внутри атома изучаем механическое движение электрона в электростатическом поле, то источником этого поля является единичный положительный заряд протона. Под каким потенциалом находится электрон на первой боровской орбите? Отвечать на такой вопрос надо предельно аккуратно. Физики и химики измерили величину энергии ионизации атома водорода из состояния основной атомной орбиты (при комнатной температуре атома):

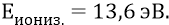
При этом над орбитальным электроном была совершена работа А («работа выхода»). Можно считать, что тот потенциал поля, под которым на этой орбите находился электрон, превратился теперь для свободного электрона в почти нулевой потенциал – как в потенциал заряда, очень далеко удалённого (через много-много орбит) от заряда ядра. Но полная энергия электрона (атома) на орбите имела величину:

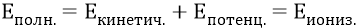
Кинетическая энергия электрона первой орбиты является базовой величиной и равна «плюс 13,6 эВ». Следовательно, потенциальной энергией электрона на орбите (энергией атома) была следующая:

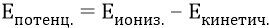
Энергия ионизации равна работе внешних сил против силы поля ядра (отрицательный заряд не приближается к ядру с помощью «положительной», в таком случае, работы поля ядра, но он удаляется от плюса ядра сторонними силами, совершающими «отрицательную» работу). Поэтому: