Полная версия
Полная версияГравитация и эфир
Следовательно, по причине большей инерционности, не столько квант-частица подстраивает под себя путь кварка, сколько «тяжёлый – инерционный» кварк подстраивает под себя путь и поляризацию значительно более лёгкой частицы эфира. Но именно из этих частиц эфира и состоит поле любой «заряженной» электромагнитной частицы – как согласованный в пространстве поток – череда поляризованных (усиленных) тяжёлой частицей квантов эфира. Мы говорим при этом в квантовой физике, что частица излучает «из себя» во все после себя стороны «струйки-потоки» («силовые линии») своего жёстко поляризованного в «тонкой» плоскости пространства поля этой частицы – как поля «излучателя».
Все события в электромагнитном мире вещества происходят в плотном супе – газе элементарных электромагнитных частиц («квантов» эфира). Эти частицы движутся в нём сумбурно – во всех возможных направлениях, с единой для каждой из них скоростью света, прошивая конструкции друг друга и вступая при этом каждый раз в очередной преонный резонанс. Но если бы мы имели возможность избирательно видеть мгновенную структуру этого газа (а будущие физики обязаны когда-нибудь научиться такому «зрению»), то мы обнаружили бы вокруг себя удивительной красоты струйки-переливы интерферирующих между собой квантовых потоков, которые были бы своими – особыми для каждой частицы «вещества» (типа электронов, нуклонов и тем более – атомов), как вещества, излучающего из себя, после себя эти переливы, «разукрашивая» таким образом сумбурное монотонное «полотно» эфира и рисуя на нём великолепные картины электромагнитного вещества природы.
Возвращаясь к атому, скажем, что если бы мы имели возможность вытащить одиночный атом в ту область эфира, где нет больше ни одной частицы «вещества» (которая умеет излучать направленные потоки квантов), а также если бы при этом нам удалось сбить-размыть «в прах-сумбур» все потоки «далёких» фотонов, прилетающих к нам от далёких скоплений вещества (звёзд, облаков газа и подобных образований), то мы бы увидели действительно чёткую-идеальную картину «холодного-прехолодного» атома, когда бы в нём, при температуре, в таком случае, абсолютного нуля, электрон-частица чётко вращался бы по тонкой-претонкой орбите, самой нижней для атома («нулевой»), радиус которой был бы в 3 раза меньшим радиуса «первой-боровской», то есть равнялся бы:
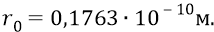
И этот электрон, кружа по этой чёткой орбите, не отклонялся бы никуда «вверх» от неё, как и «вниз» от неё. Но даже здесь мы не вполне правы. Потому что имеем в виду только возбуждения электрона под действием внешних фотонов (направленных на наш электрон струек-потоков квантов эфира). Но электрон будут держать на орбите струйки-потоки (кванты) единственного оставшегося здесь «вещества-протона». Он состоит из разно полярных кварков, включая и нейтральные (нейтрино). И поэтому этот орбитальный всё равно будет дёргаться вверх или вниз от средней орбиты, так как на него будут налетать – то «положительные» кванты (фотоны) от положительных кварков протона, то «отрицательные» кванты (фотоны) – от отрицательных кварков. Но от этих «дёрганий» нам уже не удастся избавить орбитальный электрон, да и ни к чему это делать. Потому что такая орбита будет для него всё равно наиболее гладкой из всех других возможных, возбуждаемых внешними для атома фотонами.
А теперь обратим особое внимание школьника на то важное, о чём физики ему недосказывают. Если электрон вращается, например, на первой стационарной орбите, имея там свою кинетическую энергию 13,6 эВ, и при этом, для того чтобы вырвать его из атома с этой орбиты, требуется совершить работу, сообщая электрону энергию в точности равную его кинетической энергии, то о чём это говорит? Это говорит о том, что атом держит электрон на стационарной орбите (связывает электрон с ядром) точно с той энергией, какую имеет электрон на орбите. То есть «энергия связи» электрона с атомом всегда равна кинетической энергии самого электрона:
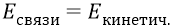
То есть атом добавляет в полную энергию системы «энергию связи»:
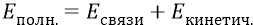
Но поскольку
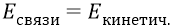
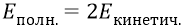
Бор прекрасно об этом знает, но он так «мудрит» со своей «сдвинутой» шкалой да с отрицательными в ней энергиями, что от школьника ускользает та простая мысль об энергии связи, которую мы только что подчеркнули.
В атоме всё предельно просто: если электрон имеет энергию, а следовательно, имеет скорость, которая его постоянно стремится вытолкнуть из атома по касательной к орбите, то для того чтобы он не улетел с орбиты, атом должен его держать (своим полем) точно с такой энергией, с какой электрон стремится покинуть этот атом. То есть физическая природа (в лице атома) сохраняет энергию «стационарного» электрона. Это и есть закон сохранения энергии в его самом прямом и красноречивом действии. Но кто непосредственно совершает саму работу по удержанию электрона? Протон ядра? Нет, не протон. Протон находится «далеко» от электрона. Работает здесь всё тот же электромагнитный эфир «в лице» поля протона. Это кванты – частицы эфира, излучаемые протоном, летят к электрону, пронизывают его конструкцию, вступая таким образом в непосредственный контакт с ним, и притягивают каждый раз каждым очередным таким квантом этот электрон ближе к протону, закругляя путь электрона в стационарную или какую другую орбиту.
Ещё раз. Какая энергия здесь сохраняется: кинетическая энергия электрона? Да, но не только она. Здесь сохраняется энергия стационарного атома с помощью энергии внешнего эфира. Кинетическая же энергия электрона (как энергия его равномерного и прямолинейного движения по инерции на каждой следующей хорде, вписанной в орбитальную окружность) непосредственно сохраняется преонным вакуумом, в котором разворачиваются вообще все атомные события, включающие в себя и все электромагнитные там поля.
И ещё раз. Атом – это очередной космический резонанс. В нём резонируют три электромагнитных тела: электрон, протон и эфир. Причём работающим телом для системы атома является эфир. Именно он поставляет энергию атому – как энергию связи электрона с протоном. У эфира этой энергии – видимо-невидимо, и он может, поэтому, сохранять один и тот же атом миллиарды лет подряд. Поскольку в атоме не изменяются (в его стационарном состоянии) ни энергия электрона, ни энергия протона, то, следовательно, вся энергия эфира (энергия связи) расходуется исключительно на повороты электрона ближе к ядру в каждой точке его перехода с хорды на хорду. Причиной этой «точки перехода» является очередной квант поля протона – как согласованный и направленный поток в сторону электрона квантов-частиц эфира.
Протон тоже является космическим резонансом. Там тоже всегда резонируют три электромагнитных тела: каждые два противоположных кварка в конструкции протона и всё тот же эфир. Правда, там работает другой слой эфира-вакуума, более высокочастотный. Этот «высокочастотный» эфир собран гравитацией в область космоса, которая называется Метагалактикой.
Электрон – это тоже космический резонанс. Там, в нём, резонируют тоже три тела: ядро электрона, сделанное из преонов, орбитальные преоны, создающие каждое электромагнитное кольцо электрона, и преонный вакуум, работающий там в виде поля ядра электрона. И этого работающего там преонного тела в природе космоса – ещё более «видимо-невидимо», чем видимо-невидимо электромагнитного эфира во Вселенной.
Сама Вселенная – это тоже космический резонанс. Там рабочим телом является гравитация, в лице квантов-частиц гравитационного вакуума. Гравитация во Вселенной удерживает в её пульсирующем объёме весь электромагнетизм, который зародился там в начале самой первой пульсации Вселенной.
Везде в космосе, где есть какая-то оформленная Им Система, нужно поискать соответствующий резонанс, который там обязательно должен быть.
* * *Теперь рассмотрим два конкретных примера в механике атома, которые продолжают классический путь исследования атомных процессов. Физики – квантовомеханики таких примеров не только не рассматривают, но не хотят, причём категорически не хотят рассматривать. И даже только этим своим нежеланием они фактически обманывают школьника, не позволяя ему, следовательно, разобраться с физикой атома. А не разобравшись с физикой, бесполезно потом городить многоэтажную математику теории «квантовой механики».
В первом примере (рис. 21.5) мы рассмотрим кинематику перехода электрона с первой орбиты (базовой – стационарной) на вторую (возбуждённую). Причём надо понимать, что вторая орбита является «возбуждённой» лишь по отношению к той первой «невозбуждённой», которая является таковой для данной, относительно низкой температуры. Но при какой-то повышенной температуре основной орбитой может быть не первая, но как раз вторая, которая при этой более высокой температуре превратится в «базовую-стационарную».
Похоже на то, что для всех самостоятельно светящихся тел базовой стационарной орбитой является не первая «боровская», но вторая «бальмеровская», с которой, поскольку она всё же «возбуждённая» какими-то процессами, электрон постоянно норовит перескочить-опуститься на первую, излучая при этом фотон видимой нашим глазом частоты (из серии Бальмера таких фотонов). Это не значит, что при этой температуре будут отсутствовать кванты (фотоны) серии Лаймана – как серии перехода электрона с возбуждённых орбит на первую боровскую, но таких переходов при такой температуре просто будет меньше в подавляющем большинстве там бальмеровских, когда возбуждённые электроны возвращаются с высоких уровней на вторую бальмеровскую орбиту.
Диаграмма перевода электрона с первой орбиты на вторую ускоряющим квантом энергии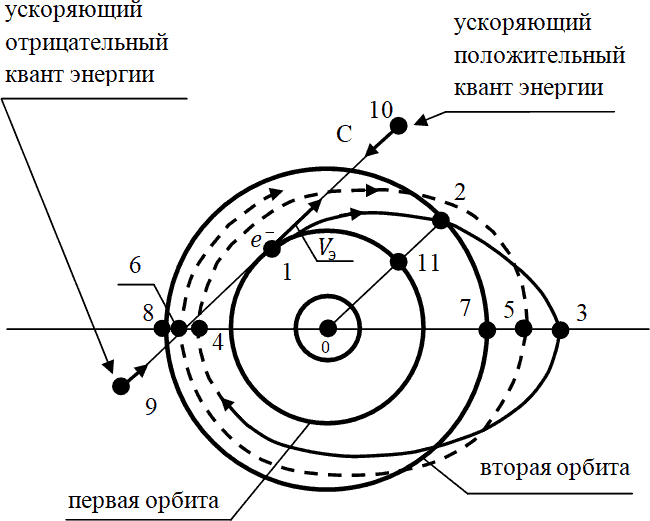
Рис. 21.5.1
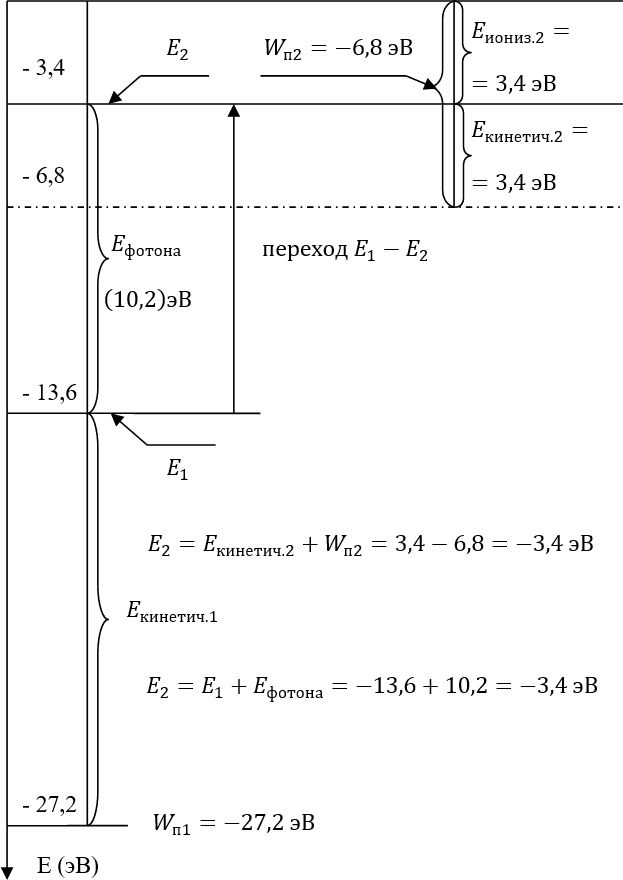
Рис. 21.5.2
Полная энергия атома для уровня второй орбиты, по расчётам квантовомехаников, составляет величину «минус 3,4 эВ», хотя у нас к этой цифре могут быть вопросы. Это значит, что энергия «минус 3,4 эВ» является тем математическим ожиданием для уровня энергии, который характерен для второй стационарной атомной орбиты. Но поскольку при такой данной температуре атом постоянно «дышит», возбуждаемый внешними «тёплыми» и видимыми фотонами, включая и редкие ультрафиолетовые и ещё более редкие в отношении каких-то наших «нормальных» условий – рентгеновские фотоны (очень энергичные), то полная энергия атома постоянно колеблется то вверх, то вниз, но колеблется около её «математического ожидания» – «минус 3,4 эВ». На нижней диаграмме рисунка 21.5 она колеблется от средней
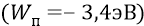
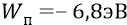
При этом мы отлично видим, что уровень этих плюс-минус колебаний в среднем равен уровню кинетической энергии электрона, которой этот электрон обладает на второй орбите.
Такие отклонения от среднего в плюс-минус сторону в математике называются «дисперсией». То есть для второй (бальмеровской) орбиты мы имеем:
математическое ожидание –
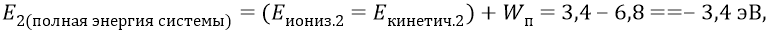
дисперсия –
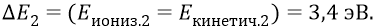
При этом дисперсия имеет знак отклонения от математического ожидания (от среднего) в обе стороны, приводя к колебаниям полной энергии в пределах от
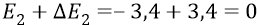
до

Исследуя таким образом любую атомную систему, мы приходим к удивительно простому по своей физике результату:
математическим ожиданием значения энергии системы, как её средним значением, является полная энергия атома –
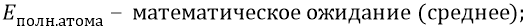
дисперсией системы является кинетическая энергия орбитального движения электрона.
Действительно, если мы остановим движение «заряда» – электрона на уровне его орбиты, обнулив таким образом его кинетическую энергию, то у системы останется лишь потенциальная энергия с «зависшим» в поле протона зарядом
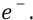
Ещё раз. Когда электрон вращался на уровне второй орбиты – как в стационарном состоянии атома, то у него была какая-то полная энергия (а на самом деле – не «у него», а у атома) – как средняя энергия этого состояния атома. Но если мы из этой средней энергии убираем (всегда положительную) кинетическую энергию движения электрона по этой орбите, то значение оставшейся энергии атома должно «провалиться» (отклониться от среднего в «минус» сторону) на значение кинетической энергии. Значит истинной потенциальной энергией атома с «зависшим» неподвижным электроном (при этом остаётся «голая» электростатика без электродинамики) является следующая:
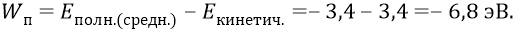
То есть имеем (по теореме вириала):
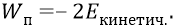
Действительно, потенциальной энергией системы тел (у нас – системы из двух «зарядов») является (по определению) работа по перемещению одного из зарядов в бесконечность, на уровень нулевого потенциала поля оставшегося (не перемещаемого) заряда. Мы говорим о перемещении отрицательного электрона. Он (в определении потенциальной энергии) перемещается с уровня второй орбиты в бесконечность. Причём работа в этом случае будет отрицательной. Почему? Потому что мы перемещаем отрицательный заряд в поле положительного (в поле протона), перемещаем его – дальше от положительного. То есть перемещаем явно – сторонними силами против действия сил самого поля. Силы в поле положительного протона будут положительными тогда, когда притягивают отрицательный заряд ближе к положительному. Тогда работа этих сил будет естественной для поля, то есть положительной, то есть такой, которую выполняет само поле. Но у нас работа отрицательна (неестественна для поля), а поэтому выполняется сторонними силами. Но по определению работы (в консервативной системе), она равна изменению потенциальной энергии, взятому с противоположным знаком:
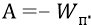
У нас потенциальная энергия (при перемещении заряда из точки орбиты в бесконечность) изменяется в положительную сторону (от значения отрицательной
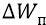
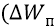
Итак, когда из самого нижнего отклонения энергии системы от её среднего (как из состояния «зависшего» без движения там «заряда» – электрона) мы приводим электрон в движение по орбите, возвращая системе её кинетическую энергию, то из максимально отрицательного значения отклоняем систему в положительную сторону до нормального среднего её полной энергии (то есть убираем отрицательную дисперсию и возвращаем в математическое ожидание – как в «нулевое среднее» по дисперсиям, сходящееся к значению математического ожидания).
Если же теперь из этого нулевого среднего мы направим на электрон стороннюю силу (в виде ускоряющего для электрона в «плюс» сторону какого-нибудь внешнего фотона – «кванта энергии»), то возбудим систему в сторону её отклонения в «плюс» энергии. Так, если энергия фотона будет равна кинетической энергии электрона (пусть мы продолжаем говорить о второй орбите), то система отклонится на «плюс дисперсию» от среднего, то есть достигнет нулевого уровня энергии системы. Если же энергия фотона в этом случае будет больше кинетической (аналогично правой диаграмме рисунка 21.4), то электрон обязан вылететь из атома с приобретённой (уже собственной) энергией электрона, равной его кинетической энергии свободного от атома электрона. Например:
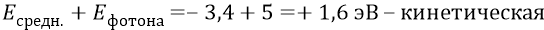
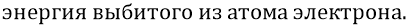
То есть такой электрон должен, по пути вылета из атома, преодолеть все положения возможных самых высоких орбит (включая какие-нибудь «тысячные» орбиты), то есть выбрать – преодолеть всю отрицательную энергию атома, достигнуть нулевой – как энергии полного разрыва с атомом, то есть должен израсходовать на это часть энергии фотона, но остаться при этом с неизрасходованной частью энергии фотона – как с «остатком» – кинетической энергией свободного электрона.
Вернёмся теперь к рисунку 21.5 в части его первой диаграммы – как к траектории классического движения электрона в кинематике его перехода с первой орбиты на вторую. Здесь электрон стартует из точки 1 орбиты под действием двух разных ускоряющих внешних фотонов («квантов энергии»).
В первом случае он ускоряется отрицательным квантом энергии, следующим из точки 9 в направление на электрон точки 1. Отрицательный квант энергии, достигнув электрона в точке 1, отталкивает электрон этим отрицательным квантом в сторону, противоположную той, откуда был испущен отрицательный квант, то есть в сторону (по касательной в точке 1) точки 10. Во втором случае электрон из точки 1 ускоряется положительным квантом энергии, следующим из точки 10 в точку 1, где он (положительный) притягивает электрон в ту точку, из которой был направлен, то есть притягивает из точки 1 (по касательной к этой точке) в сторону точки 10.
Но поскольку электрон из точки 1, с его мгновенной там скоростью
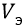
Поскольку в результате положительного ускорения электрон приобрёл дополнительную кинетическую энергию, то его начальная после этого скорость будет явно больше скорости его поступательного движения по орбите. Это значит, что вместо дуги 1–11 он пройдёт за то же «угловое» время явно больший путь какой-нибудь дуги 1–2, пересекая там уровень орбиты 2 и двигаясь далее ещё выше этой орбиты по пути 2–3, на котором радиальная составляющая его скорости будет уменьшаться под действием тормозящей силы притяжения к протону. В точке 3 он будет уже двигаться по касательной к радиус-вектору его движения в этой точке. И затем начнёт из точки 3 падать в поле протона, одновременно двигаясь поступательно по дуге 3–4. При этом падении в поле протона, его отрицательное отклонение 4–8 от орбиты 2 обязано быть меньше по амплитуде положительного отклонения 7–3 в точке апогея (максимального отклонения) эллипса от окружности 2 в точке 3. Затем, двигаясь из точки 4 по дуге 4–5 в точку 5, электрон (на первом витке эллипса) обязан пройти пока ещё выше точки 2 первого пересечения им орбиты 2 (мы имеем в виду, что переход электрона с орбиты 1 на орбиту 2 будет многовитковым – как путь постепенного уменьшения – успокоения колебательного движения возмущённого фотонным ударом электрона). Количество полных колебательных периодов будет зависеть от энергии возмущающего фотона. Если бы таковая энергия была бы значительно выше нескольких электрон-вольт (характерных для перехода с орбиты 1 на орбиту 2), то есть была бы, например, выше энергии ионизации из состояния орбиты 1, равной 13,6 эВ), то в масштабе приведённого рисунка наш электрон улетел бы из точки 1 вверх – почти по касательной 1–10 – куда-нибудь к самым верхним («тысячным») орбитам, достигнув которых, он оторвался бы от атома, продолжая и там (в масштабах рисунка) ещё пока двигаться почти по продолжению направления касательной 1–10.
Но в нашем случае «небольшого» возбуждения «небольшим» фотоном, он далее, двигаясь по дуге 4–5, пройдёт точку апогея эллипса 5 ещё ближе к орбите 2, чем на прежнем начальном витке с отклонением там 7–3. Затем, двигаясь по дуге 5–6, он достигнет точки перигея эллипса (точки 6) при отклонении от второй орбиты 6–8, меньшем, чем отклонение 5–7. И так далее – всё больше приближаясь с каждым новым витком к круговой орбите 2. Таким образом, мы рассмотрели кинематику многовиткового перехода возбуждённого электрона с первой орбиты на вторую.
Мы видим, что ни о каком «квантовом скачке» тут не может быть никакой речи. Но мы отлично помним, что эти «квантовые скачки» мгновенных переходов электрона с орбиты на орбиту приводили в глубокое отчаяние пионеров квантовой механики, таких, например, как Эрвин Шрёдингер. Но это отчаяние было тем наказанием, которое квантовомеханики получили за их отступление от классики в деле исследования ими атома. Перефразируя известную поговорку, можно сказать: «За что не боролись (за классическую механику), на то и напоролись (на неумение применить эту механику в деле исследования атома).
Анализируя философию кинематики движения электрона по стационарным орбитам, мы можем сказать, что такое движение в стабильном состоянии стационарной орбиты может продолжаться в атоме, освобождённом от внешнего на него влияния внешних фотонов, хоть миллионы лет кряду. Потому что в этом состоянии атом никак не теряет и никак не приобретает своей энергии. Вся же его потенциальная энергия – как энергия притяжения электрона к протону и имеющая отрицательное значение по отношению к средней, полностью уравновешивается кинетической энергией, возвращающей полную энергию к её средней-орбитальной для данной орбиты. То есть если электрон стабильно кружит по стационарной орбите, то это говорит только о том, что система никак не тратит энергию, а вся энергия отклонения электрона «вниз» к протону полем протона целиком компенсируется энергией его отклонения «вверх» – кинетической (инерционной).
Итак, система «электрон-протон» не имеет электромагнитных затрат на поддержание её стационарного состояния. Почему? Во-первых, потому что здесь работает третье тело – внешний эфир, который в состоянии атомного резонанса системы производит непосредственную работу по повороту электрона на каждую новую хорду квантами эфира, собранными протоном в «кванты энергии» поля протона. Во-вторых, потому что кинетическая энергия движения любого тела – это «уже приобретённая» энергия. Это энергия движения тела по инерции. Но инерция не принадлежит электромагнетизму. А это именно то положение, которое не понимают буквально все современные физики и на котором все они сломались в 20-ом веке их развития.
Ещё и ещё раз. Инерция электромагнитного тела принадлежит преонному вакууму. Именно он толкает любое тело далее, если тело «уже движется». Почему электрон на орбите «уже движется»? Потому что он сюда попал откуда-то «из бесконечности» по отношению к атому. То есть по мере его падения на ядро откуда-то издалека, он приобретал (система приобретала) не только отрицательную потенциальную энергию (теряя положительную – как энергию «поднятия» тела под полем ядра), но одновременно с этим этот электрон приобретал кинетическую энергию ускоряемого тела