
Полная версия:
Все науки. №2, 2024. Международный научный журнал
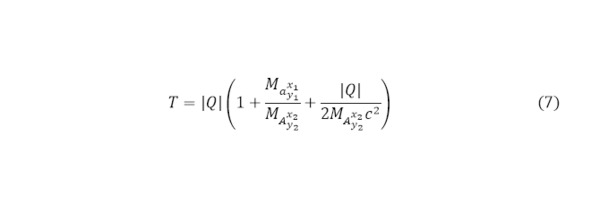
В данном случае все необходимые показатели известны и дают общее состояние реакции. Далее, желательно представлять общее энергетическое уравнение такой ядерной реакции (8), после чего можно переходить к определению кинетической энергии результатов ядерной реакции.
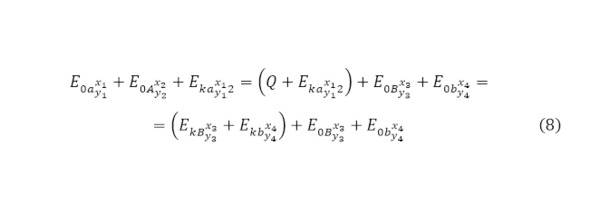
Для того же, чтобы определить кинетическую энергию продуктов ядерной реакции необходимо отметить, что каждая из частиц получает изначальный энергетический дополнительный баланс, равный сумме выхода реакции и второй кинетической энергии направленной частицы после кулоновского барьера, в обратно-пропорциональном собственной массе соотношении (9—10).
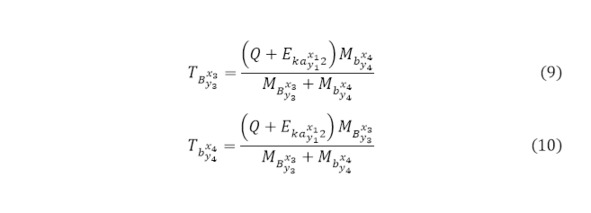
Более выраженным становиться представление этих выражений уже для трёх продуктов реакции. Чаще всего в таком случае получается момент, когда частицы разделяются на две группы – лёгкие и тяжелые группы. Лёгкая группа получает по вышеуказанным причинам большую часть от общей энергии и такой алгоритм сохраняется в соответствующим образом.
Так, если количество выходящий частиц будет стремиться к определённому большому числу (11), то их энергии будут распределяется соответствующим обратно-пропорциональным, их массе, образом (12), учитывая выход реакции (13) для такого (11).
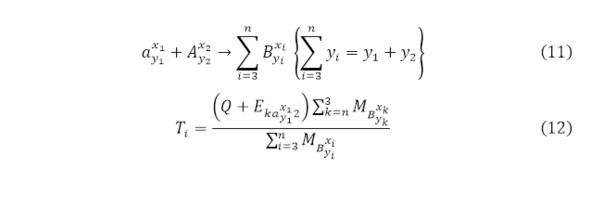
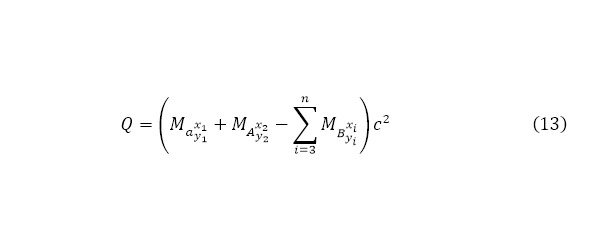
После того как определяется кинетическая энергия каждой из результатов реакции, становиться необходимым определить такое понятие как ядерное эффективное сечение ядерной реакции (14).
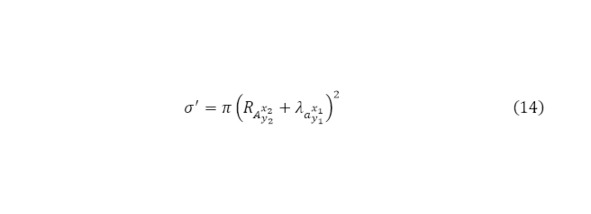
Это понятие находит своё начало в квантовой физике, согласно законам которого даже если частица не попала в физическую корпускулярную площадь ядра, то оно может быть им захвачено в следствие своей малой скорости, за счёт чего растёт волна де Бройля направленного пучка (15).
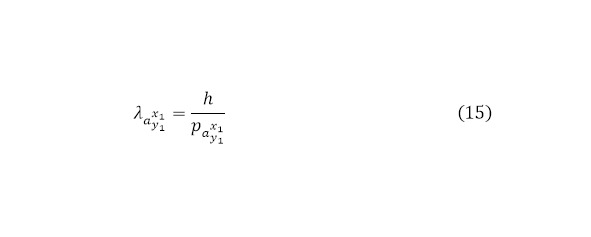
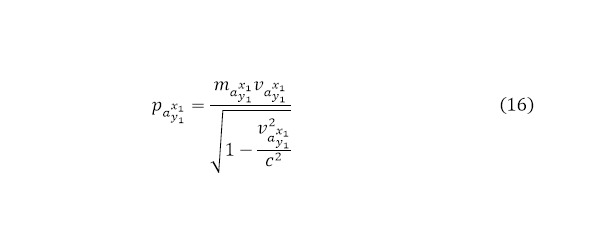
Для вычисления импульса направленной частицы при этом, согласно теории относительности используется (16), учитывая тот факт, что ядерное эффективное сечение, как и все следующие за ней функции определяются во временном масштабе после преодоления пучком кулоновского барьера, откуда и импульс, и скорости берутся непосредственно вторые, учитывая тот фактор, что за счёт увеличения ядерного эффективного сечения, кратковременно ядерные силы вместе кулоновским барьером увеличиваются в размерах.
Где скорость направленной частицы из кинетической энергии вычисляется благодаря выводу через (17).
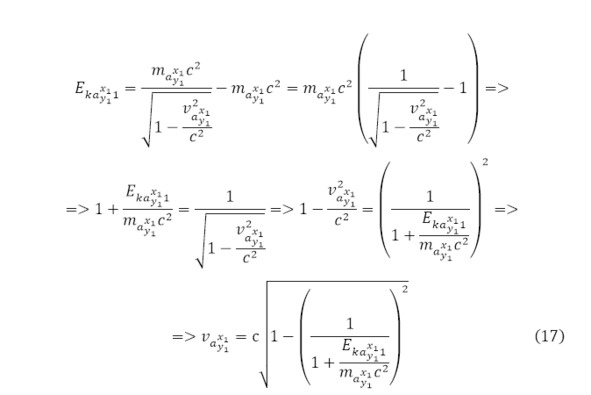
В результате проведённых вычислений удалось определить ядерное эффективное сечение, которое изменяется в квадратных метрах, однако для него введена специальная единица – барн, равная 10—28 м2 []. Но стоит указать некоторую особенность в том определении, что значение (14) является приведённым ядерным эффективным сечением, которое для практического значения переводиться через (19), где применяется константа (18), являющаяся безразмерной величиной, которая выражается через отношение практического экспериментально определённого значения ядерного эффективного сечения чаще всего используемой ядерной реакции – реакции распада урана равная 584 барна к теоретической основе, равная 3 396 747,21529 барн.

Далее, когда определено это значение, оно нужно для того, чтобы определить какая часть из всех направленных частиц действительно пройдёт через ядерную реакцию и сможет дать результат, для этого используется следующий алгоритм. Пусть на мишень налетает N (x) частиц, а после преодоления мишени, количество частиц составляет N (x) -dN, откуда dN – число всех произошедших в мишени взаимодействий. Теперь, определим, что координата на начале мишени – x, а на моменте выхода – x+dx, следовательно dx – толщина мишени. Затем вводиться определение понятия плотности ядер мишени, для того чтобы его вычислить необходимо воспользоваться (20).
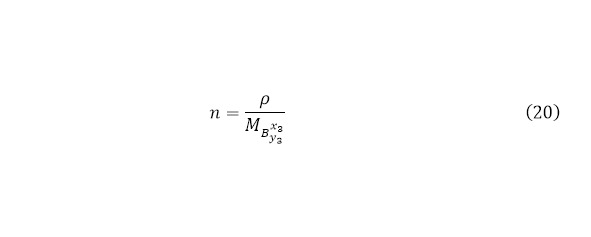
Это количество ядер, присутствующие в одном кубометре используемого вещества, следовательно, исходя из введённых определить и обозначений, можно прийти к выводу, что во всей мишени имеется (21) ядер, а если учитывать, что площадь куда попадая частицы входят во взаимодействие, считая как площадь единичного случая, куда достаточно попасть одной направленной частице, чтобы реакция произошла, принять (14), то для всей мишени это значения может быть определено согласно (22).
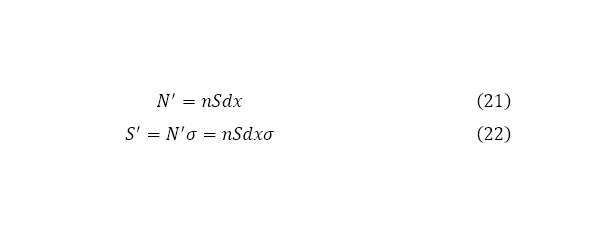
Теперь можно определить отношение всей площади, попадая на которое можно вызвать начало реакции ко всей площади мишени, которое будет равняться отношению частиц, которые вошли в реакцию ко всем частицам – функции, выражающая в начальный момент времени это значение, направленные в пучке изначально (23).
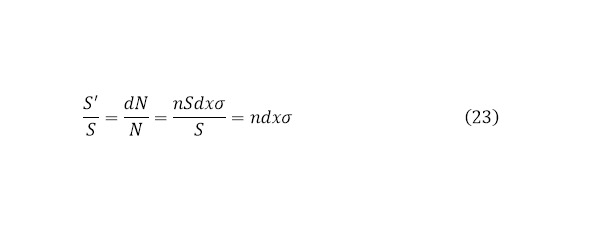
Получая такое выражение, можно проинтегрировать обе части, указав, что количество частиц, как известно – функция, которая по определённому интегралу будет брать в себе границы от изначального количества направленных частиц к количеству взаимодействий в мишени для первого интеграла. Для второй же стороны этот определённый интеграл имеет границы от нуля до значения крайней толщины мишени (24—25) [].
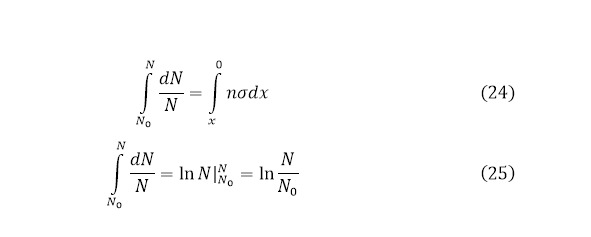
Для второго интеграла границы меняются, как и знак выражения (26) с дальнейшим преобразованием (27).
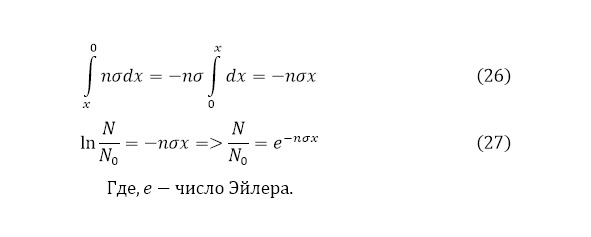
Из этого соотношения можно получить уравнение, которое бы описывало количество частиц входящих во взаимодействие (28) и откуда можно было бы вычислить процентную эффективность ядерной реакции (29).

Таким образом, можно говорить о том, что ядерная реакция прошла в количестве (28) с общей процентной эффективностью (29) с кинетической энергией для вылетающих лёгких частиц (10) и общим зарядом вылетающих частиц (30) и получаемым в результате током (31), соответствующей площадью вылетающей мишени (32), наряду со всеми учитываемыми скоростями вылетающих частиц (33).
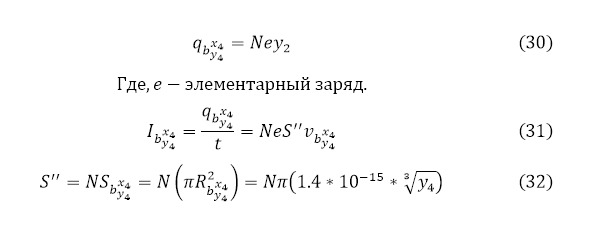
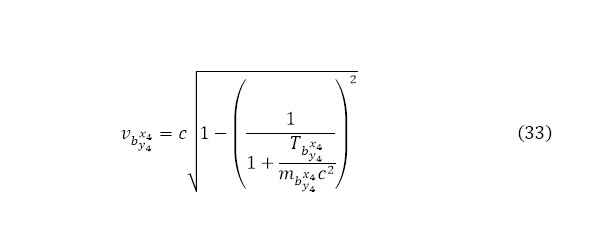
Кроме того, из (29) можно вывести и время ядерной реакции (34).
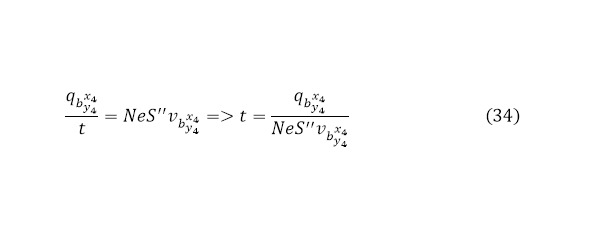
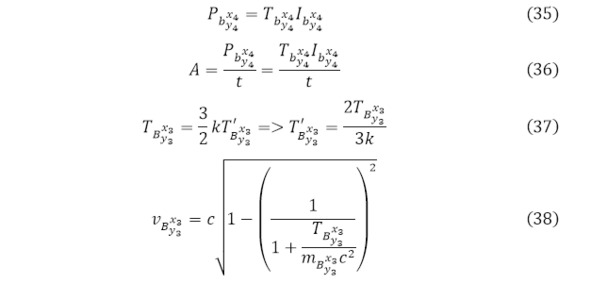
Но здесь были рассмотрены только лёгкие продукты реакции, которые в общей сумме дают мощность, определяемая через (35), как и выполняемая работа (36), а относительно тяжёлых ядер – их энергии не будет достаточной для ускорения, из-за чего она преобразуется в тепловую энергию (37) за счёт малых образуемых скоростей тяжёлых ядер (38).
Однако эта кинетическая энергия быстро распределяется по всему материалу, поэтому определённая в (37) температура относиться только к части образованных новых ядер, а для вычисления температуры мишени после реакции (39) достаточно распределить общую энергию полученных ядер на весь материал.
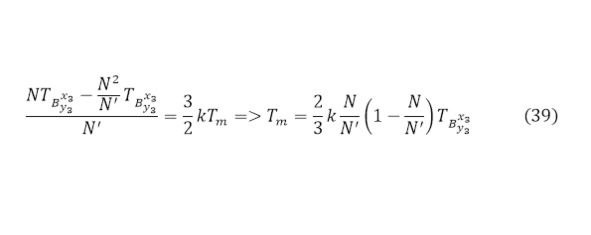
Таким образом были получены вылетающие частицы с определёнными параметрами и ядра с определёнными температурами. Однако есть такое понятие как выходящий кулоновский барьер. Величина, определённая в (3) является именно входящим кулоновским барьером, а для выходящего кулоновского барьера это выражение преобразуется как (40) с радиусом образуемого тяжёлого ядра, вычисляемый через (41).
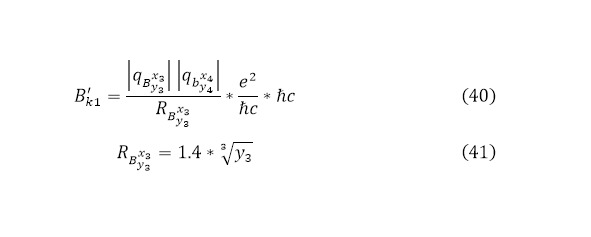
К тому же интересным является случай, когда количество частиц больше двух (11), тогда необходимо обратиться к сумме, где кулоновский выходящий барьер начинает суммироваться для одной частицы, получающая энергию от всех остальных частиц и одноимённым с ней зарядом (42—47) и здесь не учитываются соотношения с прочими частицами в пучке, поскольку это явление действует на рассеяние пучка, когда же здесь учитываются масштабы именно после ядерной реакции с близкими расстояниями.
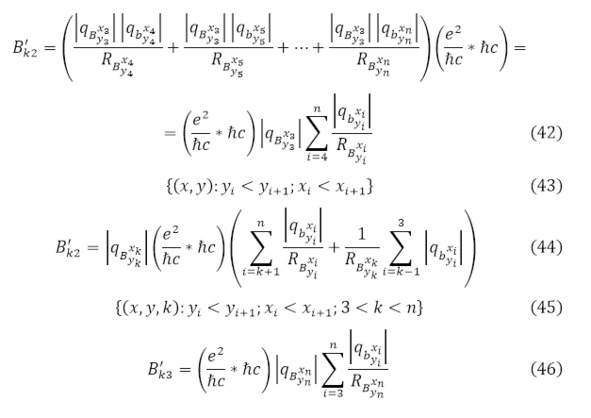
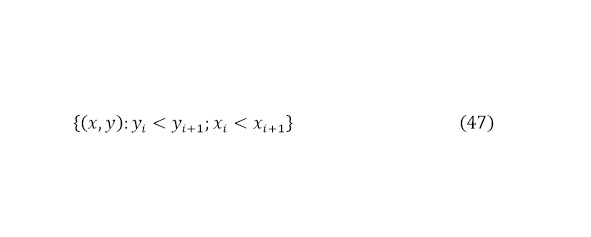
Где (42) используется для самой лёгкой частицы из всех полученных продуктов реакции в множестве (43); для всех промежуточных продуктов реакции (44) на множестве (45) с его условиями; для самой тяжёлой частицы (3.46) в масштабах множества (47).
По определению величина выходящего кулоновского барьера, как можно увидеть, описывается как энергия, которую приобретают вылетающие частицы, отталкиваясь друг от друга, сразу после преодоления ядерных сил и до убывания с ростом расстояния между ними и поэтому каждая из частиц получают эту энергию, за счёт чего, если формулы кинетических энергий лёгких продуктов реакции практически не меняются, то для тяжёлых частиц формулы (37—39) приобретают новую форму в (48—50).

Но прежде, чем продолжить анализ, стоит рассмотреть случай, когда образованное ядро может быть радиоактивным.
В таком случае стоит проанализировать реакцию вида (51).
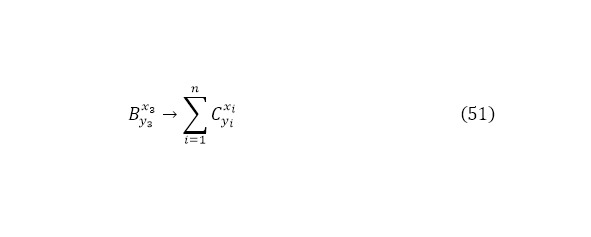
Ровно как проводился анализ для реакции (1), для реакции (51) проводиться подобный алгоритм, но, разумеется, не определяется кулоновский барьер, поскольку нет для этой реакции направленной частицы, поэтому определяется выход этой реакции (52), а затем и кинетическая энергия для всех продуктов реакции (53).
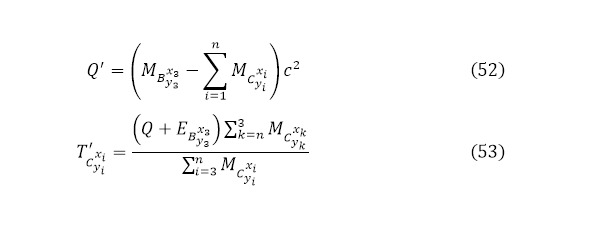
И одним из заключительных моментов анализа реакции распада является указание закона ядерного распада (54).

В данном случае, получается определённое стабильное ядро и лёгкие частицы, с определённой кинетической энергией и известной скоростью (55).
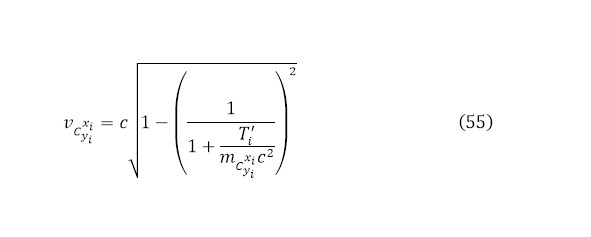
Если же настоящее ядро будет вновь радиоактивным, хотя подобные случае довольно редки, но для них действует тот же алгоритм анализа реакций распада. В данном случае также каждая из частиц будет отталкиваться, получая дополнительный выходящий кулоновский барьер, что и учитывается.
В данном случае для ядра кинетическая энергия и образуемая с его стороны температура объясняется посредством уже выведенных закономерностей для образованной части (56) и для всей мишени (57), а для лёгких частиц известна кинетическая энергия, а также заряд через (58) и ток (59).
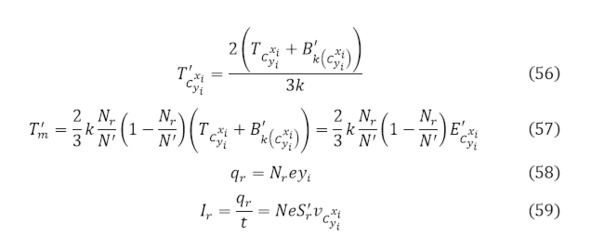
Однако, на этом не завершается анализ реакции, поскольку ныне проанализирован только один канал ядерной реакции, откуда следует, что стоит обратить отдельное внимание на все возможные различные комбинации (60).
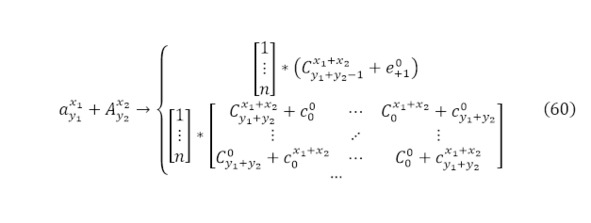
В данном случае в качестве матричного произведения выражаются все возможные вариации каналов ядерных реакций, однако, разумеется, большинство среди них, особенно те, что связанны с тяжёлыми ядрами являются маловероятными, но даже это не полный перечень, поскольку существуют также реакции, когда кинетической энергии направленных частиц становиться достаточно для создания новых частиц. Кроме того, не стоит забывать случаи, когда выходящих частиц увеличивается, то есть уже образуется 3, 4 и т. д. продуктов ядерных реакций, но только для их записи уже потребовалось использовать сложные n-мерные матрицы.
Поэтому на практике оставляются только самые вероятностные (61).
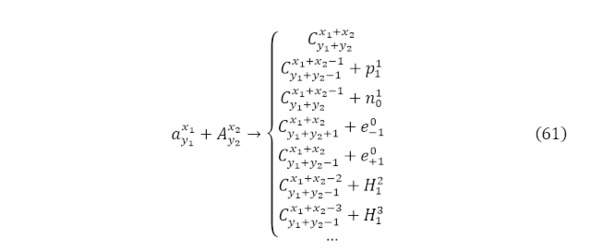
Так, если момент с образованием новых частиц не учитывается, чаще всего берутся случаи образования целостного ядра, образования протона, нейтрона, электрона, позитрона, дейтрона, тритона или прочих подобных частиц (61). Для каждой из этих реакций вычисляется выход канала ядерной реакции для всевозможных перечисляемых комбинаций, в отличие от многомерных случаев и образованием частиц (62) и для более вероятностных каналов ядерной реакции (63), вместе с порогом канала ядерной реакции также для абсолютно всех случаев, кроме вышеуказанных (64) и более вероятностных представленных каналов (65).
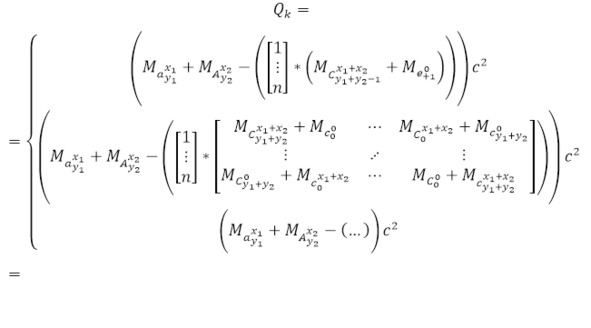
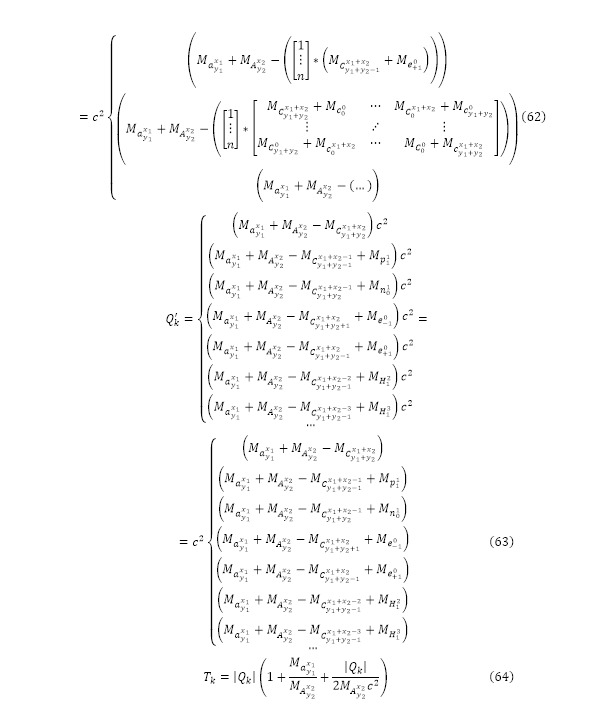
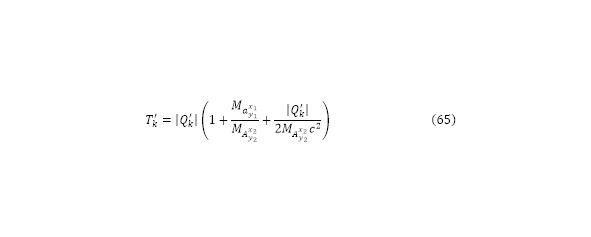
Так были определены соответствующие выражения для всех представленных каналов ядерной реакции, стоит принять истинной формулу (66), которая представляет сумму произведений всех выходов каналов на некоторое определённое число.
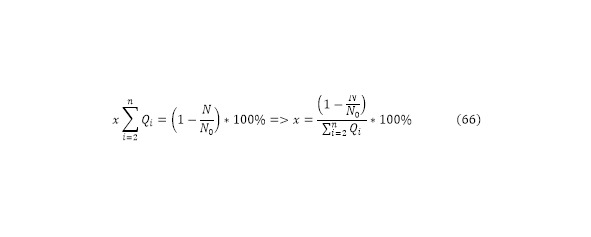
Более того, ранее был проанализирован один из каналов реакции полномасштабно, откуда было получено значение процентной эффективности этого канала (29) от разности коего вычисляется необходимый показатель. Настоящее выражение показывается, что у каждого канала есть свой процент эффективности, который в сумме составляет 100% эффективности всей реакции.
С практической точки зрения подобное можно расценивать как разделение в процентном соотношении всех направленных частиц, и каждая из них в определённой пропорции выполняет тот или иной канал реакции, разумеется, есть ещё некоторый процент приходящийся на рассеивание пучка на мишени, но это самое малое значение, после чего идут все маловероятные реакции. К тому же логично предположить, что для случаев, когда выход реакции становиться отрицательным, то есть сам канал, для коего определялся выход – эндо-энергетически, то вероятность его прохождения по сравнению с положительными экзо-энергетическими каналами становиться практически нулевой, поэтому она попросту не учитывается в уравнении.
Если же при описании каналов практически все, даже более вероятные каналы являются эндо-энергетическими, то более вероятным станет тот канал, который более близок к нулевому значению, то для есть для проведения коего нужно затратить меньшое по сравнению с прочими количество энергии. Исходя из (66) можно определить вероятность для всех каналов реакции также относительно приведённых в (62—63) выходов ядерной реакции (67—68).

Наконец, кинетическую энергию продуктов каждого из каналов реакции вполне можно определить согласно тому же алгоритму, что применялось изначально и представленные в (9—10) и (12), ровно, как и для всех ядер, по также уже представленному алгоритму. Таким образом, наконец можно говорить о том, что ядерная реакция (1), доведённая до состояния резонанса с энергиями налетающих частиц, приближенные к величине кулоновского входящего барьера была полностью проанализирована.
Выводы
Результаты анализа представляются следующим образом:
1. Условие поставленной задачи: была исследована ядерная реакция вида (1) с изначально заданными показателями в виде кинетической энергии направленного пучка и массы всех участвующих частиц в ядерной реакции в а. е. м.;
2. Направленные пучки расходуют определённое значение энергии на преодоление кулоновского барьера, обладая остаточной энергией – указывается его найденная величина;
3. Производиться перечисление выходящих частиц из основного канала ядерной реакции, в том числе различных групп гамма-квантов, если таковые имеются с указанием кинетической энергии (где при необходимости также составляется их классификация по энергиям), заряда и тока каждого из них;
4. Если образованные частицы вероятностно могут войти во взаимодействие (подобно аннигиляции позитронов и электронов), то это указывается и приводиться дополнительный список со всеми соответствующими учётами;
5. В соответствии с каждой из реакций приводиться список со всей совершаемой работой в Дж и мощностях в Вт для каждого из типов излучения со всеми составляющими. При этом указывая общие выводы по целям настоящего исследования – общее изучение / генерация электрической энергии / установление выводов по некоторому точному аспекту и т.д., а также выводы по соответствующему направлению: величина генерируемой энергии, выводы по необходимому аспекту, общие научные данные, выводы и т. д.
Заключение
На основе теоретического анализа, рассчитаны энергии образованных частиц и их характер происхождения. Исследованы ядерные реакции с бомбардирующими заряженными частицами с высокими и низкими кинетическими энергиями ядер-мишеней, а также новое введённое резонансное состояние этих ядерных реакций. Таким образом, была представлена новейшая модель исследования и анализа ядерной реакции с возможностью доведения её до состояния резонанса.
Использованная литература
1. Romanenko I.M., Holiuk M.I., Nosovsky A.V., Vlasenko T.S., Gulik V.I. Investigations of neutron radiation shielding properties for a new composite material based on heavy concrete and basalt fiber. Nuclear and Radiation Safety. 2023. Volume 3, Number 79, 42pp. – No. 472018.
2. Haubold Hans J., Kabeer Ashik A., Kumar Dilip. Analytic forms of thermonuclear functions. Physica A: Statistical Mechanics and its Applications. Volume 63015. November 2023. No. 129249.
3. Zavestovskaya I.N., Rusetskii A.S., Rusetskii A.S., Oginov A.V., Kocherov V.V., Shpakov K.V., Shemyakov A.E., Ryabov V.A. Investigation of the Yield of the Nuclear Reaction B + p – 3α Near Resonant Energy Using CR-39 Track Detectors. Bulletin of the Lebedev Physics Institute. 2023. Volume 50, Chapter 7, 279 – 284 pp.
4. Zhang H., Su J., Li Z.H., Li Y.J., Li E.T., Chen C., He J.J., Shen Y.P., Lian G., Guo B., Li X.Y., Zhang L.Y. Updated reaction rate of Mg25 (p,γ) Al26 and its astrophysical implication. Physical Review C. 2023. Volume 107, Chapter 6. No. 065801.
5. Dong G.X., Wang X.B., Michel N., Płoszajczak M., Płoszajczak M. Gamow shell model description of the radiative capture reaction B8 (p,γ) C9. Physical Review C. 2023. Volume 107, Chapter 4. No. 044613.
6. Turakulov S.A., Artemov S.V., Yarmukhamedov R. Analysis of the 12C (3He, d) 13N Proton Stripping Reaction to the Resonant State. Russian Physics Journal. 2023. Volume 65, Chapter 12, 2086 – 2093 pp.
7. Aliyev I. X. The collision energy of oncoming beams. A young scientist. International Scientific Journal. Part No.16 (306) /2020. ISSN 2071—0297. Publishing house «Young scientist». 2020. 7—10 pp.
8. Aliyev I. X., Karimov B. X. Linear electron accelerator in power engineering. An exact science. Issue No. 85. Pluto Publishing House. ISSN 2500—1132. 2020. 23—29 pp.
9. Aliyev I. X. On a heuristic idea about the emergence of a new energy technology for generating energy from resonant nuclear reactions. The international scientific journal «All Sciences». Electron Scientific School, Ridero. No. 1, 2022. 13—18 pp.
10. Aliyev I. X., Karimov B. X. Algorithm for the development of accelerator technology. The international scientific journal «All Sciences». Electron Scientific School, Ridero. No. 2, 2022. 9—16 pp.
11. Aliyev I. X. Aluminum resonant nuclear reaction. The international scientific journal «All Sciences». Electron Scientific School, Ridero. No. 3, 2022. 24—44 pp.
12. Aliyev I. X., Jalolov B. R., Karimov B. X. The role of resonant nuclear reactions in modern energy. The role of resonant nuclear reactions in modern energy. The international scientific journal «All Sciences». Electron Scientific School, Ridero. No.6, 2022. 50—113 pp.
13. Aliyev I. X. On the possibilities of mathematical apparatus on the way to creating an intuitive understanding device regarding the phenomena of electromagnetism during the simulation of plasma retention systems in systems of resonant nuclear reactions. The international scientific journal «All Sciences». Electron Scientific School, Ridero. No.6, 2023. 6—31 pp.
14. Aliyev I. X. The relevance and necessity of modern design of technologies based on neutron nuclear reactions with increased accuracy of monochromaticity when carried out on special accelerator technology. The international scientific journal «All Sciences». Electron Scientific School, Ridero. No. 7, 2023. 5—18 pp.
15. Montoya-Castillo Andresa, Markland Thomas E. A derivation of the conditions under which bosonic operators exactly capture fermionic structure and dynamics. Journal of Chemical Physics. 2023. Volume 158, Chapter 97. No. 094112.
16. Di Nitto A., Vardaci E., Davide F., La Rana G., Ashaduzzaman M., Mercogliano D., Setaro P.A., Banerjee T., Vanzanella A., Bianco D., Cinausero M., Gelli N. Clustering effects in Ar36 nuclei produced via the Mg24 + C12 reaction. Physical Review C. 2023. Volume 107, Chapter 2. No. 024615.
17. Wan, Kangnia, Li, Ming, Huang Tinga, Zhang Weia, Zhang Tianjia, Li Xiuqina, Wang Haifengd, Lv Juane. Accurate Determination of Trace Water in Organic Solution by Quantitative Nuclear Magnetic Resonance. Analytical Chemistry. 2023.
18. Kononchuk R., Feinberg J., Knee J., Kottos T. Enhanced avionic sensing based on Wigner’s cusp anomalies. International Conference on Metamaterials, Photonic Crystals and Plasmonics. No. 9482023. 13th International Conference on Metamaterials, Photonic Crystals and Plasmonics, META. 2023. No-1. 300609.
19. Mao Weia, Gong Weia, Gu Zhijieb, Wilde Markus, Chen Jikun, Fukutani Katsuyuki, Matsuzaki Hiroyuki, Fugetsu Bunshi, Sakata Ichiro, Terai Takayukig. Hydrogen diffusion in cerium oxide thin films fabricated by pulsed laser deposition. International Journal of Hydrogen Energy. 2023.
20. Godes Aleksandr I., Shablov Vladimir L. Lawson Criterion for Different Scenarios of Using D-3He Fuel in Fusion Reactors. Izvestiya Wysshikh Uchebnykh Zawedeniy, Yadernaya Energetika. 2023. Chapter 2, 134 – 147 pp.
21. Dorfman Amandaa, Wanhala Annab, Eng Peterb, Stubbs Joanneb, Colon Omara, Donetian Malika, Bracco Jacquelyn N. Inhibition of Strontium Adsorption and Desorption by Ethylenediaminetetraacetic Acid at the Barite (001) -Water Interface. Journal of Physical Chemistry C. 2023
22. Zhang Shizhenga, Xu Haoa, Xu Xing, Wei Wenqinga, Ren Jieru, Chen Benzheng, Ma Bubo, Hu Zhongmin, Li Fangfang, Liu Lirong, Yang Mingzhe, Lai Zeyu. Cross-Section Measurements of the 11B (p, α) 2α Reaction near the First Resonant Energy. Laser and Particle Beams. Volume 2023. 2023. No. 9697329.

