Геометрическая волновая инженерия: наука о новых волновых процессах

Представим на мгновение: у нас есть не просто линза, которая фокусирует свет в одну точку, а волшебное зеркало, способное собирать энергию сразу в нескольких совершенно разных местах! Именно такую картину открывают псевдоповерхности с отрицательной кривизной, обладающие несколькими зонами концентрации энергии. И самое интригующее здесь – это не просто наличие этих зон, а их глубокая взаимосвязь, словно они общаются друг с другом через саму геометрию поверхности.

Рассмотрим псевдоэллипсоид с его широкой кольцевой зоной и двумя точечными фокусами в горловинах. Если мы направим на эту структуру поток энергии (будь, то электромагнитные волны или звук), часть энергии соберется в кольце, а другая – в этих двух “бутылочных горлышках”. Но вот что удивительно: изменение интенсивности энергии в кольцевой зоне может тут же отразиться на интенсивности в точечных фокусах, и наоборот! Это, как если бы вы сжимали воздушный шарик в одном месте, и тут же чувствовали, как давление меняется в другом.

Почему так происходит? Дело в самой геометрии псевдоповерхности. Отрицательная кривизна создает хитрые “коридоры” и “перешейки”, по которым энергия может перетекать между различными областями. Волна, попавшая в одну зону концентрации, начинает многократно отражаться от искривленных стенок. Некоторые из этих отраженных волн, словно хитрые разведчики, проникают в другие области фокусировки, усиливая или ослабляя там энергию.

Взаимосвязь зон концентрации энергии открывает целый спектр новых возможностей для управления волновыми процессами. Мы можем создавать устройства, которые не просто фокусируют энергию, а динамически перераспределяют ее в пространстве, создавая сложные картины полей и взаимодействий. Это, как если бы мы получили не просто статический световой луч, а могли жонглировать несколькими лучами одновременно, управляя их яркостью и положением.

Изучение этой взаимосвязи – это своего рода “геометрическая алхимия” для волн. Понимая, как форма поверхности влияет на перераспределение энергии между различными фокусами, мы можем научиться создавать совершенно новые типы волновых устройств с беспрецедентными возможностями.

Псевдоповерхности третьего порядка открывают новое измерение в ГВИ: возможность описывать и проектировать устройства в которых траектория, фаза, спектр и локализация волны управляются не материалами, а пространственным уравнением формы. Это превращает инженерию волн в инженерную геометрию. Их изучение требует синтеза дифференциальной геометрии, спектральной теории, численного моделирования и новых методов топологического анализа конструкций.

Таким образом, псевдоповерхности третьего порядка представляют собой следующий шаг в развитии ГВИ – переход от статических и единичных фокусных устройств ко множественным, адаптивным, нелинейным волновым системам, способным выполнять многозадачные, мультиспектральные и энергосберегающие функции в самых разных приложениях – от фундаментальной физики до телекоммуникаций и медицины.

4.1 Псевдосфера 3-го порядка

Псевдосфера 3-го порядка представляет собой расширение классической псевдосферы Бельтрами, широко известной как модель поверхности с постоянной отрицательной Гауссовой кривизной (K = const <0). В рамках геометрической волновой инженерии (ГВИ), псевдосфера является ключевым референсным элементом – "эталоном" гиперболической геометрии. Однако в чистом виде её применение ограничено из-за математической идеализации и трудности физической реализации. Поэтому возникает необходимость в более реалистичной и инженерно полезной модификации этой геометрии – Псевдосфере 3-го порядка.

Псевдосфера 3-го порядка – это геометрическая структура, имеющая ту же гиперболическую основу, что и стандартная псевдосфера, но с добавленными параметрами и элементами, характеризующими более высокую степень геометрической сложности: переменной кривизной, асимметрией, фокусными деформациями и нелокальными топологическими эффектами.

1. Геометрическое определение

Псевдосфера классически получается вращением цепной линии (цепной кривой) вокруг своей горизонтальной оси. При этом образуется поверхность постоянной отрицательной Гауссовой кривизны.

Базовый элемент псевдосферы 3-го порядка – это сечение псевдосферы 2-го порядка.

Псевдосфера 3-го порядка строится вращением базового элемента вокруг новой оси симметрии, параллельной оси фокусов и сдвинутой на расстояние R.

Псевдосфера 3-го порядка имеет переменную отрицательную Гауссову кривизну.

Энергия собирается в центральном кольце и не зависит от оси симметрии.

Псевдосфера 3-го порядка отличается следующим:

– Гауссова кривизна K = κ1·κ2 больше не является постоянной, она меняется по координатам z и r:

K (z, r) = −K0 + DK (z, r),

где DK (z, r) – локальные вариации кривизны, формирующие особые зоны локализации и дефокусировки.

– Ось вращения может быть смещена или наклонена, что разрушает строгое осевое изотропное поведение и создаёт условия для анизотропной фокусировки.

– Поверхность может быть искусственно "обрезана" вертикально или горизонтально (отрезки, полу поверхности), чтобы придать конструкции определённые габариты или реализуемые формы.

2. Общие характеристики геометрии

– Наличие центральной области с почти постоянной кривизной (ядро гиперболизма);

– По мере удаления от центра – плавные переходы к участкам с меньшей или переменной K < 0;

– Геометрия допускает наличие перегибов, асимптотических краёв, геометрических «капель», образующихся в результате z3-слагаемого;

– Границы могут вызывать зеркалообразные отражения или "утечку" волн при особом импедансном проектировании.

3. Волновые особенности и поведение

Псевдосфера 3-го порядка обладает всеми классическими волновыми преимуществами гиперболических поверхностей, но развивает их за счёт следующих уникальных свойств:

Модифицированное гиперболическое расхождение

Из-за переменной кривизны, геодезические линии, хотя и сохраняют свойство расходимости (экспоненциальное удаление), могут формировать зоны равномерного покрытия, эргодических траекторий, участков повторной встречи и «кратеров локализации».

Стоячие волновые модуляции

В отличие от классической псевдосферы, где волна быстро уходит, здесь могут формироваться устойчивые стоячие моды – как радиальные, так и кольцевые – за счёт несоответствия между кривизной и геометрической длиной волновой петли.

Эффекты кольцевой циркуляции

Благодаря гладкому изменению формы и скорости отклонения геодезик, возможна само поддерживаемая волновая циркуляция, напоминающая азимутальные моды в тороидальных резонаторах, но реализуемая без замкнутого тора.

Нелинейная локализация

При наличии волны с сильно выраженной амплитудой и L, сравнимой с геометрическими особенностями (область перегиба, перегруженности), происходит эффект дифракционно-индуцированной «ловушки» – волна концентрируется в области отклонения метрики.

Топологическая сегментация модуляцийРазные частоты или моды, входящие с разных зон, могут быть разнесены геометрией по разным траекториям распространения – по сути, это пространственно-селективный фильтр на базе формы.

4. Применения

– Геометрически селективные резонаторы с регулируемым добротным контуром, чувствительным к амплитуде;

– Фокусирующие безлинзовые элементы в ТГц- и инфракрасном диапазоне;

– Обратные рассеиватели и ловушки для энергии: волна входит, многократно отражается, поглощается в центре (аналог «оптической чёрной дыры»);

– Устройства короткоживущей памяти: стоячая волна удерживается только определённое время, затем рассеивается (для кодирования информации);

– Интерферометрические элементы с пространственной модуляцией фазы и траектории.

5. Реализация

В отличие от идеальной псевдосферы Бельтрами, псевдосфера 3-го порядка может быть реализована физически:

– В печатных структурах (3D-формы);

– В метаповерхностях: за счёт пространственно изменяемой толщины, перфораций, мета атомов;

– В полупрозрачных мембранах или гибких материалах с контролем кривизны на микро- и нано уровне;

– На фотонных чипах – за счёт гравировки диффузных криволинейных волноводов.

6. Символическое и практическое значение в ГВИ

Псевдосфера 3-го порядка – это не просто геометрический объект высокой степени, это концептуальный переход ГВИ от идеализированных моделей к адаптивным, инженерно-реализуемым структурами, в которых:

– управление волнами осуществляется не только через форму, но и через нелинейность этой формы;

– геометрия становится одновременно средой, функцией и алгоритмом;

– устанавливаются мульти фокусные, многомодовые и согласованные флуктуационные режимы.

Такой объект можно рассматривать как «волновую оболочку интеллекта», способную адаптироваться и перераспределять энергию между зонами в зависимости от внешних условий, начальной фазы и частоты сигнала.

Таким образом псевдосфера 3-го порядка – ключевой элемент в арсенале геометрической волновой инженерии следующего поколения. Её глубокая геометрическая структура создаёт условия для устойчивого управления волнами за счёт пространственной организации. Это – многофункциональное, многозонное, интеллектуальное тело, где каждый элемент отражает связанное взаимодействие между формой и полем. Её использование открывает путь к новым классам встраиваемых волновых устройств – волновых процессоров, резонаторных триггеров, геометрических фильтров и адаптивных линз с распределённой «геометрической логикой»

4.2 Псевдогиперболоид 3-го порядка

Псевдогиперболоид 3-го порядка представляет собой логическое и функциональное развитие псевдогиперболоида 2-го порядка – одного из базовых элементов в геометрической волновой инженерии (ГВИ). В отличие от второго порядка, где геометрия задаётся вращением профиля с гладким изменением кривизны, поверхность третьего порядка строится на основе более сложной, нелинейной образующей кривой, содержащей члены высших порядков (например, z3, r3, z2r), а также может включать локальные перегибы, седловые узлы, само перекрывающиеся участки и топологические особенности.

Псевдогиперболоид 3-го порядка – это высоко комплексная псевдоповерхность, предназначенная для реализации продвинутых сценариев управления волнами: удержание и замедление, пространственное кодирование, фильтрация по длине волны, трассировка по частотным каналам, многократная фокусировка и динамическая реакция на возмущения. Благодаря своей геометрической сложности, он способен к самоорганизации волновых траекторий и формированию многозонных резонансных состояний, не свойственных более простым структурам.

1. Геометрическая структура

Псевдогиперболоид 3-го порядка характеризуется высоко ориентированной гиперболической формой с геометрически вложенными структурами и переменной (нелинейной) Гауссовой кривизной K(z,r).

Базовый элемент псевдогиперболоида 3-го порядка это сечение псевдогиперболоида 2-го порядка.

Псевдогиперболоид 3-го порядка строится вращением базового элемента вокруг новой оси симметрии, параллельной оси фокусов и сдвинутой на расстояние R.

Псевдогиперболоид 3-го порядка имеет переменную отрицательную Гауссову кривизну.

Концентрация энергии зависит от оси симметрии и может располагаться в следующих местах:

a) ось симметрии параллельна оси фокусов гиперболы – зона концентрации энергии представляет собой две коаксиально размещённые цилиндрические области.

b) ось симметрии перпендикулярна оси фокусов гиперболы – две кольцевые области сверху и снизу

Такой профиль допускает более одного экстремума, что приводит к сложной форме с несколькими узкими горловинами (перешейками) и промежуточными «камерами» или расширениями.

– Структура может включать симметричные и асимметричные боковые воронки, седловидные перегибы, изогнутые и скрученные поверхности, направленные волноводы.

– Гауссова кривизна становится непрерывной функцией координат и может менять знак локально, сохраняя в среднем K < 0. Это создает "острова" геометрической изоляции или усиления, топологически встроенные в основную оболочку.

– Инженерная реализация может быть открытой (двусторонней), полузамкнутой (например, горлышко с отражающей шапочкой) или объемно-резонаторной с множественными слоями кривизны внутри.

2. Волновые свойства

По сравнению с псевдогиперболоидом 2-го порядка, структура третьего порядка демонстрирует качественно новые режимы взаимодействия с волнами:

Многозонная фокусировка

– Волна не просто фокусируется в минимуме радиуса, как в классическом гиперболоиде, а испытывает серию последовательных пере фокусировок при движении вдоль поверхности.

– Формируются несколько взаимосвязанных «фокусных узлов» или фокус-областей, каждая из которых имеет собственные спектральные характеристики.

Эргодические и квазихаотические режимы

– Геодезические траектории, распространяющиеся вдоль поверхности, не замыкаются коррелировано, а покрывают структуру квазиравномерно, формируя спиралевидные, квадратичные или обратные циклы.

– Это делает поверхность полезной для статической и динамической декогерентной фильтрации (режим «хаотического подавления резонансов»).

Волновые ловушки двойного уровня

– Перешейки (узкие участки) могут работать как барьеры, затрудняющие выход волны, создавая области временного накопления поля – аналог фотонного или акустического "капкана".

– Воздействие волны меньшей частоты может быть локализовано в первом перешейке, тогда как высокая частота проходит дальше и фокусируется во внутренних каналах.

Эффекты волновой памяти и обратной связи

– Благодаря сложной обратной геометрической связи между зонами, возбуждение в одной области влияет на модовые картины в других зонах.

– Такие поверхности могут "запоминать" форму волны – например, сохранять стационарную моду до момента вмешательства, что полезно для волновых схем памяти и считывания.

3. Сравнительные особенности

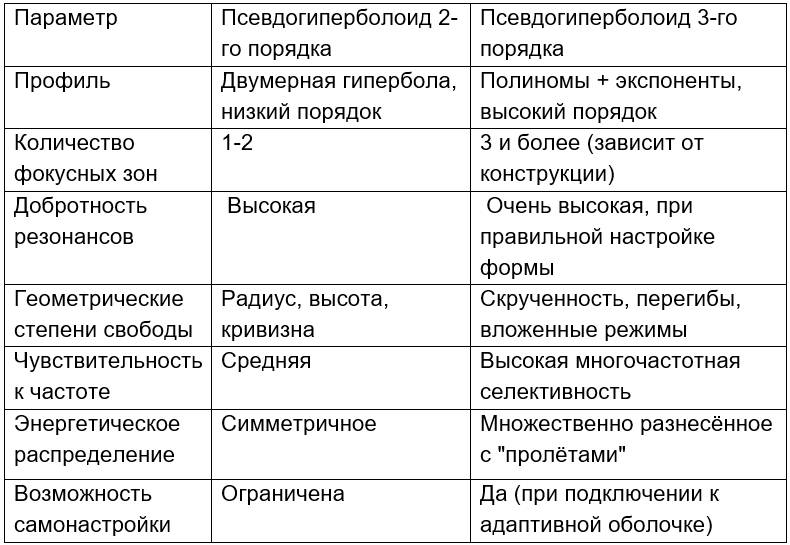
4. Инженерные применения

Псевдогиперболоид третьего порядка является универсальной волновой платформой, включающей свойства многократных отражений, направленного распространения, осевого резонанса и перенастраиваемости. Применения включают:

– Многомодовые резонаторы для квантово-фотонных приложений (оптические кристаллы, фотонные ловушки);

– Реализуемые мета поверхности для ТГц волн с возможностью пространственного частотного фильтра;

– Акустические и ультразвуковые ловушки для удержания частиц или создания низкопотерьных стоячих волн;

– Сенсорные системы с несколькими зонами чувствительности (многоточечное откликание);

– Пассивно-активные архитектуры для распределённой обработки сигналов, включая аналоговые волновые вычисления;

– Волновые переключатели и селекторы частот, управляемые формой; следует отнести сюда также спектрально-пространственные маршрутизаторы.

5. Методы реализации

Современные материалы и технологические процессы позволяют реализовать такие геометрии уже сегодня:

– 3D-печать диэлектрических и композитных основ с нано метровой точностью;

– Гибридные нано мембраны с эффектом управляемой деформации;

– Создание "воксельных оболочек" со встроенной программируемой кривизной;

– Метаповерхности с переменным фазовым откликом, имитирующие геометрию на волновом уровне.

Таким образом псевдогиперболоид 3-го порядка – это квинтэссенция идей ГВИ: пространство становится вычислительным и управляющим элементом. Эта структура выступает как многослойная, саморегулируемая, многофункциональная платформа для волнового взаимодействия различных типов и частот, создавая условия резонанса, адаптации и автоматической перенастройки без использования электроники.

В условиях растущего интереса к неэлектронным, волновым и топологическим вычислениям, созданию энергоэффективных сенсоров, когерентных накопителей и распределённых коммуникационных структур, псевдогиперболоид третьего порядка становится основой для архитектур "интеллектуального пространства" – среды, в которой форма определяет функцию, а геометрия диктует логику.

4.3 Псевдопараболоид 3-го порядка

Псевдопараболоид 3-го порядка – это усовершенствованная геометрическая структура в классе аксиально-симметричных псевдоповерхностей с переменной отрицательной кривизной (K < 0), представляющая собой развитие идей, заложенных в конструкции псевдопараболоида 2-го порядка. В отличие от последнего, где профиль задаётся кривой второго порядка и ограничен одной максимум-фокусной зоной распределения энергии, псевдопараболоид третьего порядка использует образующие более высокой математической сложности (например, полиномы третьей степени, синусоиды с модуляцией, экспоненциальные изгибы), что позволяет формировать гораздо более сложную фокусно-резонансную структуру. Это обеспечивает целый спектр новых режимов управления волновыми процессами, включая глубокую фокусировку, волновые ловушки, пространственное зонирование энергии и многочастотные резонансные состояния.

Такой объект демонстрирует переосмысленную парадигму направления и локализации волн через нелинейную пространственную метрику, трансформируя традиционный подход к фокусировке в комплексное управление фазой, плотностью энергии, резонансом и взаимодействием между зонами.

1. Геометрическая структура

Базовый элемент псевдопараболоида 3-го порядка – это сечение псевдопопараболоида 2-го порядка.

Псевдопараболоид 3-го порядка строится вращением базового элемента вокруг новой оси симметрии, параллельной оси фокусов и сдвинутой на расстояние R.

Псевдопараболоид 3-го порядка имеет переменную отрицательную Гауссову кривизну.

Концентрация энергии зависит от оси симметрии и может располагаться в следующих местах:

a) ось симметрии параллельна оси фокусов ветвей парабол – область концентрации энергии формируется в центральной цилиндрической зоне.

b) ось симметрии перпендикулярна оси фокусов ветвей парабол – область концентрации энергии формируется в двух кольцевых зонах сверху и снизу

Архитектурно псевдопараболоид 3-го порядка включает:

– Одну центральную продолговатую фокусную зону, поддерживаемую протяжённым каналом с управляемой отрицательной кривизной;

– Несколько локальных мини-фокусов вдоль высоты, обеспечивающих каскадное распределение энергии;

– Плавные или ступенчатые изменения кривизны от вершины к основанию;

– Возможность формирования "резонансной камеры" – области, в которой вся волна может временно стабилизироваться.

Гауссова кривизна K (r z) изменяется неравномерно и многозонно, порождая внутренние перегибы (κ1 и κ2 переходят в точки минимума или даже нуля). В отличие от псевдогиперболоида, здесь аберрации вынесены за пределы фокусной зоны – что делает усиление более узконаправленным и "программируемым".

2. Волновые эффекты

–Глубокая фокусировка с регулируемой протяжённостью

Псевдопараболоид 3-го порядка создаёт объёмную фокусную зону, вытянутую вдоль оси. За счёт смены кривизны происходит не только продольная концентрация волн, но и поперечная модуляция плотности поля.

–Множественная фокусировка (каскадная)

Наличие в профиле z3-компоненты создаёт условия для появления временных или пространственно распределённых подфокусов – участков временного усиления, используемых для задержки, демодуляции, селективной фильтрации.

–Геометрические резонансные ловушки

При определённой частоте и соотношениях между размерами поверхности и длиной волны (L), внутри тела образуются области стоячих волн – «волновые зоны памяти», сохраняющие амплитуду дольше, чем в обычных резонаторах.

–Селективная пространственная фильтрация

Разные траектории для разных частот позволяют пространственно разделять сигналы. Низкие частоты создают широкие фокусные зоны, в то время как высокие уносятся ближе к основанию.

–Фазовая стабилизация

При попадании в зону переменной кривизны волна «замедляется» и перестаёт флуктуировать – это создаёт эффекты временной привязки фазы, полезные в квантовой и когерентной оптике.

3. Применения

Благодаря своей геометрической ответственной архитектуре, псевдопараболоид 3-го порядка находит применение в системах, где требуется:

– Пространственная концентрация энергии без точечного перегрева или искажений (фокус без фокуса);

– Многозонный сенсинг – датчики давления, температуры, колебаний, распределённые по длине структуры;

– Терагерцовые резонаторы с селекцией частоты за счёт формы, а не фильтров;

– Ультразвуковые линзы высокой разрешающей способности (например, в медицине);

– Элементы направленной акустики и фазового звукового ландшафта;

– Спектрально-пространственные маршрутизаторы – устройства, где входной фронт разбирается на фрагменты по геометрическим диапазонам.

4. Сравнение с Псевдопараболоидом 2-го порядка

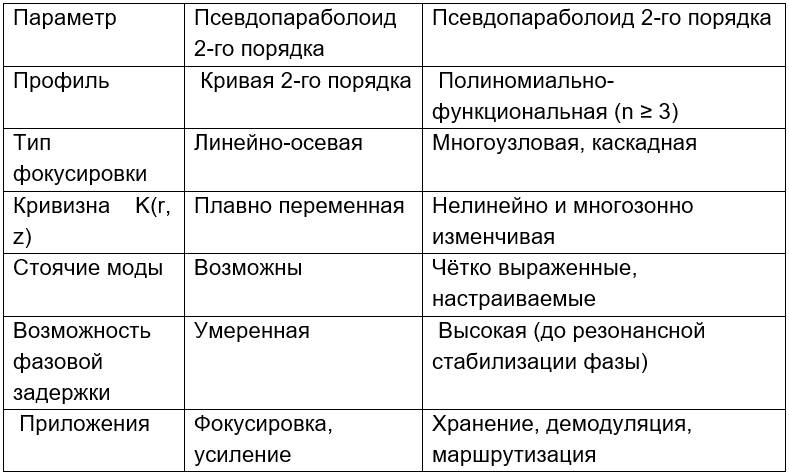
5. Инженерно-конструктивные аспекты

Реализация псевдопараболоида 3-го порядка возможна в различных масштабах:

– Макроуровень: 3D-печать, формовка из композиционных материалов с диэлектрическими или акустическими свойствами;

– Микроуровень: структурирование многослойных подложек, органических пленок и фото активных слоёв;

– Нано уровень: ионно-лучевая литография, нано маскирование и осаждение в мета поверхностных технологических цепочках;

– Интеграция: применение в гибридных фотонных чипах, акустических микросхемах, гибких волноводных структурах.

Таким образом псевдопараболоид 3-го порядка – это интеллектуальная геометрическая конструкция в ГВИ, где форма перестаёт быть вспомогательным элементом, а становится самостоятельным управляющим инструментом. Он позволяет организовать не просто фокусировку волновой энергии, а целую цепочку адаптивных волновых реакций, скрытую в закодированной кривизне.

Такая поверхность – прямой путь к созданию геометрически программируемых волновых устройств: от когерентных накопителей и резонаторов до распределённых сенсоров, фильтров, антенн и логических структур. Псевдопараболоид 3-го порядка – это уже не просто поверхность. Это топологически активный элемент будущих волновых технологий.

4.4 Псевдоэллипсоид 3-го порядка

Псевдоэллипсоид 3-го порядка представляет собой усовершенствованную топологическую структуру в рамках геометрической волновой инженерии (ГВИ), которая формирует новую категорию многофокусных, адаптивных и энергоаккумулирующих псевдоповерхностей с переменной отрицательной Гауссовой кривизной K (z, r) < 0 и сложной пространственной связностью.

В отличие от псевдоэллипсоида 2-го порядка, где основной акцент делается на симметричное кольцевое распределение фокусной энергии и линейную трансляцию волн вдоль оси, псевдоэллипсоид 3-го порядка использует более сложную образующую кривую третьего или смешанного порядка (в том числе нелинейные тригонометрические и экспоненциальные компоненты), благодаря чему достигается усиление пространственной кооперации волн, создание многоуровневой резонансной структуры и распределённой тепловолновой/акустоэлектромагнитной памяти в объёме.

Это устройство – не только геометрическая форма, но виртуальный «волновой организм», в котором энергия циркулирует между зонами, обмениваясь фазовой и частотной информацией через геометрически запрограммированные траектории.

1. Геометрическая структура

Базовый элемент псевдоэллипсоида 3-го порядка – это сечение псевдоэллипсоида 2-го порядка.

Псевдоэллипсоид 3-го порядка имеет переменную отрицательную Гауссову кривизну.

Концентрация энергии зависит от оси симметрии и может располагаться в следующих местах:

a) ось симметрии параллельна оси фокусов эллипсов – зона концентрации энергии представляет собой две коаксиально размещённые кольцевые области.

b) ось симметрии перпендикулярна оси фокусов гиперболы – две кольцевые области сверху и снизу.

Ключевые особенности геометрии:

– Многозонная распределённая форма: как минимум одна зона расширения (экваториальная), две «горловины» (верхняя и нижняя части), возможны дополнительные внутренние камеры;

– Постоянная или переменная осевая асимметрия, вызванная нелинейными членами образующей;

– Топологическая многоосность: существуют изолированные волновые «ниши», в которые волна может попасть только по определённой траектории;

– Переменная кривизна K (r, z), включая зоны перегибов, кривизны близкой к нулю, и резкую смену геометрического градиента.

Поверхность может иметь как замкнутую, торообразную форму с частично перекрывающимися стенками, так и полуоткрытые каналы на концах/экваторе для лазерных, акустических или ТГц-волновых входов/выходов.