Lippincott's Magazine of Popular Literature and Science, Vol. 22, August, 1878

A score of music in the new style of notation has no signature—that is, no flats or sharps at the beginning. Above the line of numerals is written simply "Key of G," "Key of A flat," etc. The pitch, of course, must be taken from the tuning-fork or a musical instrument, as it is in all cases.

Second. The same idea should always be presented by the same sign: the same sign should always represent the same idea.

It has already been shown how this principle is disregarded; but take, for further illustration, the symbols indicating silence. There are seven different kinds of rests, and there is no need of more than one. These signs are:

Again: these rests may be followed by one or two dots, which increase their duration. For example: an eighth-note rest dotted equals an eighth note and a sixteenth; and followed by two dots it equals an eighth, a sixteenth and a thirty-second note in time. That is, the first dot prolongs the rest one-half or a sixteenth, and the second dot prolongs the value of the first dot one-half or a thirty-second.

To a disciple of Galin it is really amazing that such a bungling, unscientific way of expressing silence should have been tolerated so long. Compare these "pot-hooks and trammels," dotted and double-dotted, with Galin's symbol of silence, the cipher (0)! This is all, and yet it expresses every length of rest, as will be shown presently.

Let us now examine the symbols representing the prolongation of a sound. There are three ways by the common notation, where there should be but one. First, by the form of the note itself, as—

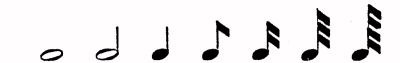
Second, by one or more dots after a note, the first dot prolonging the note one-half, and the second dot prolonging the first in the same ratio. Third, by the repetition of the note with a vinculum or tie, the second note not being sung or played. Galin uses simply a dot. It may be repeated, as a rest or a note may, but then its value is not changed, any more than in the case of notes or rests repeated. For example:

Here are the first measures of a well-known hymn in common time, four beats to the measure. As all isolated signs, whether notes, prolongations or rests, fill a unit of time, or beat, it follows that the dots following sol and mi prolong these through an entire beat, for the dots are isolated signs. Whatever the time, each unit of it appears separate and distinct to the eye at a glance; and all the notes, rests or prolongations that fill a beat are always united in a special way. This will be more fully shown hereafter.

Third. Elementary textbooks or methods should never present two difficulties to the mind at the same time; and such textbooks or methods should be an assemblage of means adapted to aid ordinary intelligences to gain the object proposed.

The first thing that the student of music encounters is a staff of five lines, armed with flats or sharps, the signature of the key, or with no signature, which shows that the music upon it is in the key of C. On this staff he sees notes which are of different pitch, and probably of different length. In any case, there are at least three difficulties presented in a breath—to find the name of the note, give it its proper sound, and then its proper length; and these difficulties are still greater because the ideas, as we have seen, are hidden under defective symbols.

Take all the teachers of vocal music, says M. Chevé, place them upon their honor, and let them answer the following question: "How many readers of music can you guarantee by your method, out of a hundred pupils taken at random and entirely ignorant of music, by one hour of study a day during one year?" The reply, he thinks, will be: "Not many." And if you tell them that by another method you will agree in the same time to teach eighty in a hundred to read music currently, and also to write music, new to them, dictated by an instrument placed out of sight or from the voice "vocalizing," they will all declare that the thing is impossible.

The great composers and renowned performers are cited as examples of what the ordinary methods have accomplished. No, replies Chevé: they are exceptional organizations. The methods have not produced them. They have, on the contrary, arrived at their proficiency despite the methods, while thousands fail who might reach a high degree of excellence but for the obstacles presented by a false system to a clear understanding of the theory of music, which in itself is so simple and precise. In the study of harmony especially, says the same authority, does the want of a clear presentation of the theory produce the most deplorable results. It has made the science of harmony wellnigh unintelligible even to those called musicians. Ask them why flats and sharps are introduced into the scales; why there is one sharp in the key of G major and five in B major; why you spoil the minor scale by making it one thing in ascending and another in descending—that is, by robbing it of its modal superior in ascending and of its sensible in descending. They will in most cases be unable to answer, for neither teachers nor textbooks explain. The catechisms found in most of the elementary works upon music are replete with stumbling-blocks to the young musician. Mr. R. H. Palmer, author of Elements of Musical Composition, Rudimental Class-Teaching and several other works, says in one of his catechisms that "there are two ways of representing each intermediate tone. If its tendency is upward, it is represented upon the lower of two degrees, and is called sharp; if its tendency is downward, it is represented upon the higher of two degrees, and is called flat. There are exceptions to this, as to all rules." This is deplorable. Music is a mathematical science, and in mathematics there is no such thing as an exception to a rule. But to quote further from the same catechism: "A natural is used to cancel the effect of a previous sharp or flat. If the tendency from the restored tone is upward, the natural has the capacity of a sharp; if downward, the capacity of a flat. A tone is said to resolve when it is followed by a tone to which it naturally tends." How long would novices in the science of music rack their brains before they would comprehend what the teacher meant by a tone tending somewhere "naturally," or by the tendency of a restored tone being destroyed by the "capacity of a flat"? The same writer, speaking of the scale of G flat, says it is a "remarkable feature of this scale that it is produced upon the organ and piano by pressing the same keys which are required to produce the scale of F sharp." This is precisely equivalent to saying that it is a remarkable feature that the notes C, D, E, F are produced by pressing the same keys which are required to produce do, ré, mi, fa.

One more citation from the same author. Speaking of the formation of scales, he says: "Thus we have another perfectly natural scale by making use of two sharps." This vicious use of the term "natural" is deplorable, because it is apt to give the pupil the notion that some scales are more natural than others. A certain note is called "C natural," and it is not uncommon for learners to suppose that it is easier or more natural to sing in that key, as it is easier on the piano to play anything in it because only the white keys are used, while in any other at least one black key is required. Indeed, a pupil may study music a long time before he finds out that there is no difference between flats and sharps, as such, and other notes—that all notes are flats and sharps of the notes a semitone above and below. Seeing the staff of a piece of music armed with half a dozen sharps or flats, the first thought of the pupil is that it will be rather hard to sing. And many really suppose that flats and sharps in themselves are different from other notes—a little "flatter" or "sharper" in sound perhaps—and secretly wonder why their ear cannot detect it. Of course it may be said that there is no necessity for pupils to have such absurd notions, but it is inevitable where the theory of music is made so difficult for the beginner. No doubt the ambitious and naturally studious will delve and dig among the rubbish of imperfect textbooks, analyzing and comparing the explanations of different teachers, until order takes the place of chaos; but textbooks should be adapted to ordinary capacities, and thereby they will better serve the needs of the most brilliant.

Fourth. The memory should never be drawn upon except where reasoning is impossible.

In science you have general laws, and from these deduce particular facts depending upon them, but collections of facts and phenomena without connection you must learn by heart. The extensive and involved nomenclature of music, added to the complicated and inconsistent system of notation, is a continual and exhausting strain upon the memory. Teachers commence their drill in vocalization, as a rule, with the scale of the key of C, and the pupils, fired with a noble ambition to become musicians, make a strenuous effort to remember where do, ré, mi and the other notes are placed on the lines and spaces of the staff. Presently the "key is changed," and with that change comes chaos. All the notes are now on a different series of lines and spaces. The confusion continues until the series of seven notes is exhausted. Then come scales with new names, commencing upon different notes (flats and sharps), but with places on the staff identically the same as others having different names!

Long before this point is reached by the pupil his courage flags, his ambition cools, and in the greater number of cases dies out altogether. To be sure, if he has the rare courage to persist he will come to recognize the notes of any key, not by the number of lines or spaces intervening between them and some landmark, but by their relative distances from each other measured by the eye. But this requires long practice. At first he must remember if he can, and when he cannot he must count up to his unknown note from some remembered one. It is, at best, a labor of Sisyphus. With many people—bright and intelligent people, too—it requires years of practice to read new music at sight even tolerably readily; for it is not simply a question of learning the notes, difficult as that may be: there is a further difficulty, and to many even a greater difficulty—that of the measure. Not the number of beats in a measure or bar and their proper accentuation—this is but the alphabet of time—but to group correctly and rapidly the fractional notes, rests and prolongations in their proper place in time. In very rapid music this becomes an herculean task, requiring long-continued and arduous practice. It is not simply a question of nice appreciation of rhythm, but of mathematical calculation, to know instantly and unhesitatingly, for example, that one-sixteenth, one half of one-sixteenth and one thirty-second added together equal one-eighth—that is, one-third of the unit of time or beat in six-eighths time.

Any one can see that such mental feats, ever varying as they are in music, and demanding instant solution at the same time the attention is given to the intonation, style, etc., must require an exceptional temperament and natural capacity. The fact is, it is beyond the power of most musicians. They must practise their instrumental and vocal music, and learn it nearly "by heart," before they attempt to perform it for others.

The writer of this has attended a class taught by one of Chevé's pupils, and can testify to the efficiency of the method, though the lessons were a very modest attempt to exemplify the perfection of the system. The lessons of M. and Mme. Chevé were divided into three parts: first, a drill in the principles of the theory of music; second, singing scales and exercises; third, drills in "reading time," beating time, analyzing time, etc., ending with some diverting "round" or "catch" or some exercise in vocal harmonies. On their method of teaching time, more than on any other part of their system perhaps, did the grand success of the Chevés depend. Rhythm was always taught separately from intonation, it being contrary to their principle to present two difficulties together before each had been mastered alone.

The first grand law of Galin's system is that every isolated symbol represents a unit of time or beat, whatever the measure. For example:

The second law is that the various divisions of the unit of time are always united in a group under a principal bar, and such a bar always contains the unit of time—never more, never less. To illustrate:

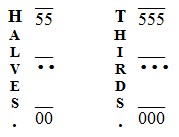
Here the units of time—the numeral, the dot and the cipher—are divided first into two equal parts, and then into three. In both cases the groups represent units of time—one beat of a measure—according to the rule. It will be noticed that the form of the notes is the same whether whole or divided into fractions; that is, there are no different forms for "crotchets," "quavers," "semiquavers," etc., the expression of time being better provided for. Thus, halves or thirds are indicated to the eye by a single bar surmounting two signs for halves, three for thirds. If the halves or thirds have in their turn been divided by two, then the principal bar covers two little groups of two signs each; if the halves or thirds have been divided by three, then each principal bar covers two or three little groups of three signs each.

Nothing could be more simple than this. The eye has always before it, separate and distinct, the unit of time or beat; and the mind apprehends instantly the number of articulated sounds, prolongations or silences (rests) that must be sung or played during that beat. The eye has no hesitation, the mind no calculation, as to what note commences or ends a beat. Even the most modest student of music will see the immense advantage of this. Nor is there any need for the multiplicity of fractions to express different kinds of time. The moment the eye rests upon the score the student knows the measure as definitely and certainly as he knows the letters of the alphabet.

"And is this all there is in this system of notation?" some one will ask. Practically, Yes. There are the symbols of intonation, the numerals and the dot—the dot below or above the notes showing the octave (

); the two diagonal lines indicating flats or sharps (

); the horizontal bar indicating the time (

); and the vertical line or bar dividing the measures ( 1 2 3  | 4 3 2  | ).

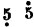
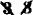
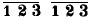
The following is the air "God Save the Queen!" or, as we call it, "America," written in this method. The lower line, of course, is the alto:

KEY OF G.

It will be noticed that the dot in the second measure which prolongs the note si ( 7 ) is not placed against it, as we are accustomed to see it. It is carried forward into the second beat, where it belongs. There it is grouped with the note do ( 1 ), and occupies one half of that unit of time; for all the signs grouped under a line or under the same number of lines are equal in time to each other, the same as all isolated signs are. In the sixth measure the dot is isolated; therefore it fills the whole beat, while the following beat is represented by a rest ( 0 ). In two of the measures there are groups of two notes. Each of the notes in these groups of course equals in time half of an isolated note, for each occupies half the time of one beat.

The French say déchiffrer la musique—to puzzle it out, to decipher it, as one would say of hieroglyphs on an Egyptian sarcophagus. The term is well chosen. The causes of the obscurity of musical notation are numerous, but the most prolific is undoubtedly expressing time by the form of the symbols of sound. In slow movements, and where only few modulations occur, this does not seem to be a serious objection; but in the rapid movements of compound time it becomes insupportable—at least after one has learned that there is a better way. An example in 6⁄8 time—six eighth-notes to the measure—will illustrate this:

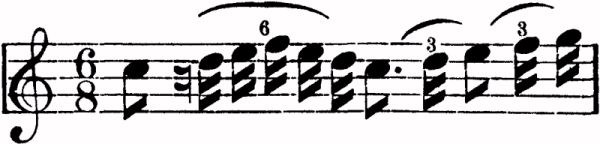
Here each triplet fills the time of one-third of a beat; that is, three-sixteenths equal one-eighth, according to the sublime precision of the old notation! But then no such thing as a twenty-fourth note is in use: three twenty-fourths would just do it! This is a part of a vocal exercise. The learner would have to divide each beat into three parts each, unless very familiar with such exercises; and one of these divisions would fall on a rest, another in a prolongation, another in the middle of an eighth note. In the new method see how the crooked places are straightened:

It "sings itself" the moment you look at it, after a little study of this rational notation. Note also that there is no mathematical absurdity here: the division is logical, and yet the air is perfectly expressed in every particular.

The mastery of time in music is at best an arduous task, yet teachers of music, as a rule, expect their pupils to learn it incidentally while studying intonation. They give no special drill in pure time at every lesson; and the result is that army of mediocre singers and players who never become able to execute any but the very simplest music at sight. They may know the theory of time, may be able to explain to you clearly the divisions of every measure, but this is not sufficient for the musician: he must decipher his measures with great readiness, precision and rapidity, or he never rises above the mediocre. The ambition to excel without hard labor is the bane of students of the piano especially. It leads them to muddle over music too difficult for them; finally, to learn it after a fashion, so that they may be able to "rattle and bang" through it to the delight of fond relatives and the amazement and pity of severe culture. Not that we should have consideration for all that passes for severe culture and exquisite sensitiveness among musical dilettanti. In no field of art is there so much affectation, assumption and charlatanry as in music. Some years ago a musician in New York of considerable reputation refused to play on a friend's piano because, as he said, it was a little out of tune and his ear was excruciated by the slightest discord. The lady wondered that the instrument should be out of tune, as it was new and of a celebrated manufacturer. She sent to the establishment where it was made, however, and a tuner promptly appeared. He tried the A string with his tuning-fork, ran his fingers over the keyboard, declared the piano in perfect tune, and left. That evening the musician called, and was informed that a tuner had "been exercising his skill" upon the instrument. Thereupon he graciously condescended to play for his hostess, and the sensitiveness of his ear was no longer shocked. She never dared to undeceive him, but mentioned the fact to another musician, a violinist, who exclaimed, greatly amused, "The idea of a pianist pretending to be fastidious about concord in music! Why, the instrument at its best is a bundle of discords." Both of these musicians were guilty of affectation; for, although the piano's chords are slightly dissonant, the intervals of the chromatic scale are made the same by the violin-player as by the pianist. What right, then, has the former to complain? To be sure, the violinist can make his intervals absolutely correct: he can play the enharmonic scale, which one using any of the instruments with fixed notes cannot do. But does he, practically? Does he not also make the same note for C sharp and D flat? The violinist mentioned of course alluded to the process called equal temperament, by which piano-makers, to avoid an impracticable extent of keyboard, divide the scale into eleven notes at equal intervals, each one being the twelfth root of 2, or 1.05946. This destroys the distinction between the semitones, and C sharp and D flat become the same note. Scientists show us that they are different notes, easily distinguished by the ear. Representing the vibrations for C as 1, we shall have—

each note being increased by one twenty-fourth of itself, or in absolute vibrations—

[* 'Opus Chords' font was used for the sharps and flats. If this is not available, click a sharp or flat note to see an image (transcriber).]

This is the enharmonic scale, having twenty-one notes. The chromatic has eleven, and the name—it may be remarked in passing—is from the Greek word for "color" χρωμα because the old composers wrote these notes in colors, and had them so printed. Not a bad idea, surely: many a learner on the piano would be overjoyed to see all the ugly flats and sharps on the staff in brilliant holiday dress.

There is no reason at this day, when science in all fields is making such progress, why the ordinary music-teacher should have so limited a knowledge of his subject. He should be able to explain the fundamental principles of the different scales upon the theory of vibration, and to so educate the apprehension of his pupils that they will not be content with the imperfect catechisms of the music-books in vogue. And with the adoption of a rational system of writing music, which will reduce the time and labor of learning it to one half, there will be time for the niceties of a science of such vast importance to the culture—and, indirectly, to the moral progress—of the world.

MARIE HOWLAND.

SAMBO: A MAN AND A BROTHER

"But," I said eagerly, "you do not deny that slavery was a curse to the country—to Southerners most of all?"

"My dear fellow," said Captain S–, knocking off the ashes from his cigar, "don't go into that! We were talking about negroes, not about slavery. I suppose," he added meditatively, "there are not many men in the country who have faced more of the negro race than those of us who spent some part of our term of service in the Freedmen's Bureau. Imagine settling disputes from morning till night between negroes and between negroes and whites! If you abolitionists—as you called yourselves before the emancipation—want to have some of the romance and sentiment of negroism dissolved, live amongst them for a time."

"You were in Virginia?" I said.

"Yes, but the negroes there are a better class than in the States farther South and more remote from cities."