Полная версия:
Слова и числа
[?-4]
Попробуйте разделить все буквы русского алфавита, цифры и буквы английского алфавита на топологические классы эквивалентности (кроме, состоящих из нескольких не соединяющихся элементов, букв Ё, Й, Ы). Для упрощения работы, показаны характеристические фигуры каждого класса для букв русского языка.
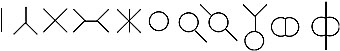
Не буквой единой…
Если посмотреть на стандартную клавиатуру компьютера, то главное место на ней занимают буквы русского и английского алфавитов с возможностью переключения с одного алфавита на другой и со строчных букв на прописные. Но это не всё. Для записи речи используются в языке знаки препинания или пунктуации.
Знаки препинания – это элементы письменности, выполняющие вспомогательные функции разделения (выделения) смысловых отрезков текста, предложений, словосочетаний, слов, частей слова, указания на грамматические и логические отношения между словами, указания на коммуникативный тип предложения, его эмоциональную окраску, законченность, а также некоторые иные функции. Знаки препинания, синтаксически оформляющие текст, облегчают его зрительное восприятие и понимание, а при воспроизведении текста вслух помогают осуществить его интонационное оформление (интонация, смысловые паузы, логические ударения).
Какие же знаки мы найдем на клавиатуре, следовательно, и в печатных текстах? Точка, запятая, точка с запятой, двоеточие, многоточие, восклицательный знак, вопросительный знак. Это наиболее распространенные знаки препинания, которые не имеют каких-то модификаций и не требуют особых пояснений. Другие же используемые знаки бывают весьма неоднозначны и требуют некоторых пояснений.
Дефис – короткая черточка для разделения каких-либо слов и переносов, ничем не отбивается от соседних букв. Обратите внимание на разницу в знаке тире и дефиса в данном тексте. Тире стоит между первыми двумя словами текущего абзаца. Оно отбивается пробелами от слов с обеих сторон. Как только мы сделали отбивку пробелами, черточка сразу становится длиннее, хотя набиралась с помощью той же клавиши, что и дефис. Между двумя датами ставится тоже тире, но оно не отбивается пробелами и поэтому зрительно выглядит как дефис (1945-2020), но называется короткое тире.
Богаты в своем разнообразии знаки скобок. Скобки – это чаще всего парные знаки. Обычно первая в паре скобка называется открывающей, а вторая – закрывающей. Самые распространенные виды скобок круглые ( ), квадратные [ ], фигурные { }. Далее существуют скобки угловые. На компьютерной клавиатуре для них нет специальных клавиш, но их можно поставить с помощью имеющихся математических знаков меньше и больше < >. В «вордовском» редакторе формул угловые скобки есть. Можно поставить скобки косые, используя знак косую черту – «слеш», причем есть косая черта с наклоном в ту или иную сторону / /, \ \. Можно поставить скобки прямые, у математиков это будет означать модуль числа | |, или даже двойные прямые скобки || ||.
Скобки широко используются в математике, гораздо шире, нежели в русском языке. Возьмем, например, круглые скобки. В русском языке они употребляются для выделения пояснительного слова или вставного предложения. Непарная закрывающая скобка может использоваться при нумерации пунктов перечисления. Ниже, перечисляя случаи применения круглых скобок в математике, мы одновременно показываем два случая применения их в русском языке.
В математике круглые скобки показывают приоритет математических и логических операций. Кроме того используются для:
1) выделения аргументов функции;
2) записи координат векторов;
3) записи биномиальных коэффициентов;
4) обозначения матриц;
5) обозначения открытого геометрического или числового промежутка;
6) обозначения скалярного произведения векторов и смешанного (тройного) скалярного произведения;
7) обозначения периода в позиционной записи дробной части рационального числа.
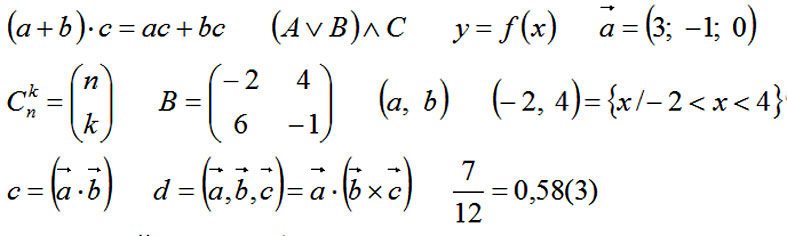
Перейдем к скобкам квадратным. В лингвистике их употребляют для обозначения транскрипции (ёж [jош]). Квадратными скобками в цитатах задают авторский текст, который проясняет контекст цитаты. «Еще они [скобки] используются в библиографических записях и сносках».
Квадратными скобками в математике обозначается операция взятия целой части числа. Они применяются для задания приоритета операций (аналогично круглым) в качестве скобок «второго уровня», для обозначения векторного произведения векторов, для обозначения закрытых промежутков. Квадратные скобки могут использоваться как альтернатива круглым скобкам при записи матриц и векторов. Одинарная квадратная скобка объединяет совокупность уравнений или неравенств.
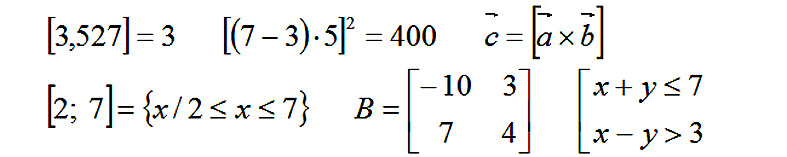
На компьютерной клавиатуре нет еще двух видов квадратных скобок, которые используются в математике, но знакомы далеко не всем учителям. Это модификации квадратных скобок под названием «пол» и «потолок» для обозначения ближайшего целого, не превосходящего х, и ближайшего целого, не меньшего х, соответственно:
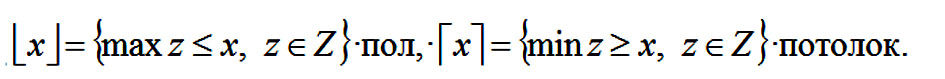
Таких скобок нет на клавиатуре компьютера, но они есть во встроенном в офисный Word редакторе формул, который математики используют для записи формул, содержащихся внутри обычного текста.
Фигурные скобки вообще вотчина математиков. Я даже не знаю, где их используют в русском языке. Фигурными скобками в одних математических текстах обозначается операция взятия дробной части числа, в других – они применяются для обозначения приоритета операций, как третий уровень вложенности (после круглых и квадратных скобок). Фигурные скобки применяют для обозначения множеств. С этим мы уже сталкивались в соответствующем разделе и в текущем изложении примеров применения скобок. Одинарная фигурная скобка объединяет системы уравнений или неравенств, служит для обозначения кусочно-заданной функции.
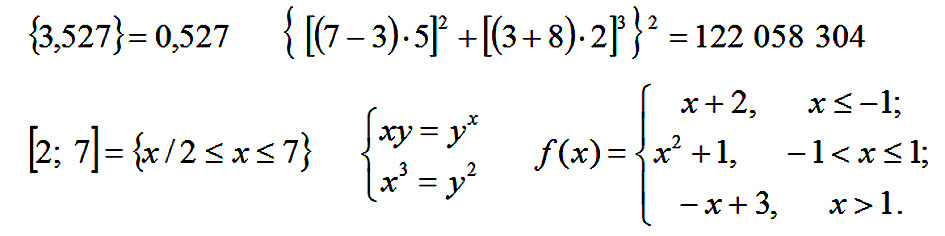
Прямые скобки используются в математике для обозначения модуля числа или модуля вектора, определителя матрицы:
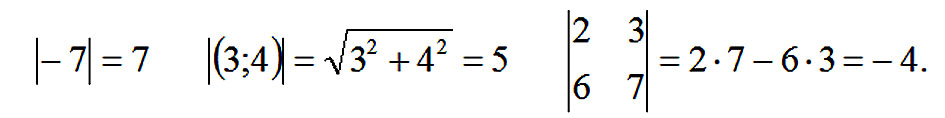
У остальных скобок более редкое и специфическое использование, поэтому не будем загромождать текст. Скобки могут применяться в паре со скобкой другого вида или удваиваться каждая. Вариантов множество.
Перейдем к следующим знакам препинания – кавычкам. Слово «кавычка» имеет русское происхождение и означает «крючковатый знак». Так как это всегда парный знак, термин употребляется во множественном числе. Они тоже весьма разнообразны. Кавычки парный знак препинания, который употребляется для выделения прямой речи, цитат, отсылок, названий предприятий, литературных произведений, газет, журналов, а также отдельных слов, если они включаются в текст не в своём обычном значении, используются в ироническом смысле, предлагаются впервые или, наоборот, как устаревшие и тому подобное. В отличие от скобок – это не математический знак, а чисто литературный.
В русском языке традиционно применяются французские «ёлочки», а для кавычек внутри кавычек и при письме от руки – немецкие „лапки“. Кавычки-елочки есть с русской раскладке клавиатуры. При нажатии после пробела двух клавиш Shift+2 появятся открывающие кавычки, а при нажатии этих же клавиш после слова или цитаты, автоматически появятся закрывающие кавычки. При английской раскладке клавиатуры набираются английские “кавычки”, причем они могут быть как двойные, так и ‘одинарные’. Употребление их вместо «ёлочек» в русском тексте, для выше перечисленных целей, – неправильно. В текстах на русском языке в английские одиночные кавычки, согласно принятым правилам, берётся текст, указывающий значение некоторого слова или словосочетания (обычно иноязычного). Лингвистика, от лат. lingua – ‘язык’.
В британском английском языке пользуются ‘английскими одиночными’ для кавычек первого уровня и “английскими двойными” для ‘кавычек “внутри” кавычек’. В американском английском – наоборот. Также в английском языке (особенно в его американском варианте) точка и запятая зачастую ставятся перед закрывающей кавычкой, а не после, как в русском.
Интересный вопрос, как поставить немецкие кавычки „лапки“ на клавиатуре компьютера, ведь они отличаются от английских “кавычек” и на клавишах их нет?
Для этого используем правую цифровую часть клавиатуры. Нажмите клавишу NumLock, чтобы загорелся соответствующий индикатор справа. Включите русскую раскладку. Зажмите Alt и наберите код открывающей или закрывающей кавычки:
0132 для левой кавычки-лапки „
0147 для правой кавычки “
Цифры набираются на правой части клавиатуры. После набора четырёхзначного числа отпустите Alt и появится требуемый знак.
Другой путь – это воспользоваться меню Вставка-Символ и в открывшемся окне вы найдете любые кавычки, которые вам потребуются.
Как-то так получилось, что форма и вид кавычек зависят от национальности: у разных стран разные кавычки, хотя правила их применения в принципе одинаковые. Не будем рассматривать все национальные кавычки, так как они вряд ли нам встретятся.
Существуют еще так называемые "компьютерные кавычки" – кавычки особого типа, в которых рисунок открывающих и закрывающих кавычек совершенно не различается. Такие кавычки встречаются в текстах, набранных с помощью компьютерной клавиатуры. Изменяя в меню Параметры Word, мы можем менять раскладку клавиатуры и кавычки «ёлочки» будут заменены кавычками "компьютерными".
Как видите, знаки пунктуации весьма многообразны, поэтому мы рассмотрели только основные. К ним можно отнести словоразделитель – пробел.
Человек обладает богатой фантазией, так как умеет мыслить. Кто-то обратил внимание, что из всех знаков препинания только два (! и ?) придают предложению эмоциональную окраску. Еще в 1969 году Владимир Набоков в одном из интервью высказал мысль, что следовало бы придумать специальный знак пунктуации для выражения эмоций. Время властно переводило записи от авторучек к клавиатуре. Сначала к клавиатуре пишущих машинок, затем к клавиатуре компьютера. Зафиксировано, что в 1982 году Скотт Фалман, ученый из университета Карнеги-Меллон, первым в мире придумал сочетание скобок, тире и двоеточия для выражения положительных эмоций в переписке и предложил использовать вот такую последовательность символов для обозначения шутливых сообщений: :-) и символы для обозначения не шутливых сообщений :-( Изображения расположены горизонтально, читать их следует наклонив голову налево. Первоначально подобные изображения получили названия эмотиконы, то есть иконки с эмоциями, но в дальнейшем за ними утвердилось название смайлики, так как первое изображение соответствовало улыбке. Поняв идею смайлика люди стали творить с помощью знаков препинания.
Вместо фраз, которые призваны передавать эмоции автора, дабы не тратить время на тщательный подбор соответствующих слов, используются специальные значки, которые составляются из обычных печатных знаков, имеющихся на клавиатуре компьютера: букв, цифр, знаков препинания и т. д. Использование «смайликов» ускоряет составление письма при неформальном общении и придает ему оригинальный вид. Думается, начало свое они берут от восклицательного и вопросительного знаков, которые в отличие от других знаков препинания (точки, запятой, двоеточия, тире, точки с запятой) уже содержат в себе некоторую эмоциональную окраску. Подобным образом используются восклицательный и вопросительный знаки в шахматной нотации, чтобы отметить в записи партии сильный (!) или слабый ход игрока (?). Дальнейшее развитие идеи шло в соответствии с детской присказкой: «точка, точка, запятая – вышла рожица кривая». С помощью печатных знаков рисовались условные изображения повернутого на 900 человеческого лица, с определенным эмоциональным выражением. Поэтому подобное явление получило название типографика, то есть изображение, сделанное типографскими знаками. Допустимое в частной переписке, оно совершенно неуместно в деловом общении. Особенность классических смайликов – в горизонтальном расположении вертикальных зон лица.
Вот, в качестве примера, несколько популярных смайликов, сделанных типографскими знаками.
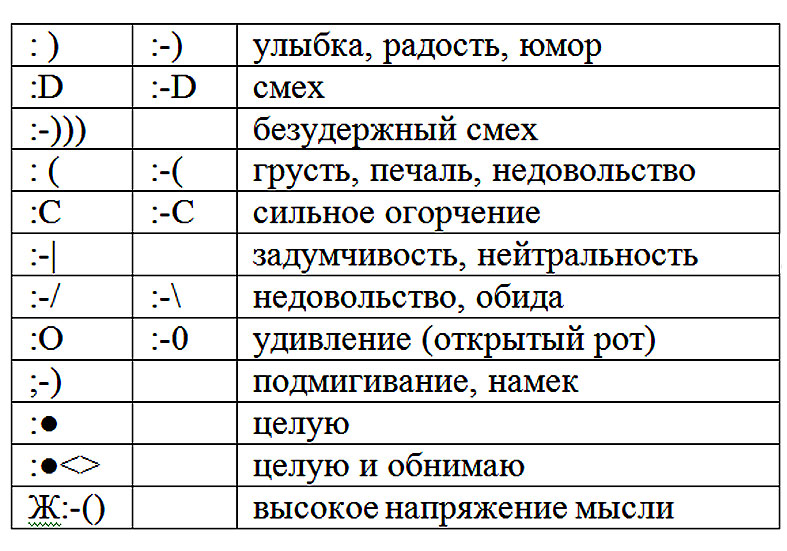
С развитием компьютерной графики получили распространение смайлики, не связанные с типографскими знаками, знаками препинания и клавиатурой.
Американский художник Харви Болл в декабре 1963 года первым создал графическое изображение улыбки в виде двух точек и дуги в жёлтом круге. Представители страховой компании State Mutual Life Assurance Cos. of America обратились к художнику, и тот нарисовал им первую фирменную «улыбку». Первая серия смайликов вышла в качестве жёлтых значков, которые были подарены служащим и клиентам компании. Логотип имел успех, значков наштамповали более 10 тысяч.

(Сайт freeimg.ru/kartinka/863628)
Дальше пошло, поехало. Сегодня в разных соцсетях можно увидеть множество смайликов. Разновидностей этих значков очень много. Некоторые из них обозначают не только эмоции, но и состояния человека и его внешности. Очень симпатичны смеющиеся, улыбающиеся смайлы. Бывают задумчивые, нейтральные, удивленные значки. Чего только не увидишь в разросшемся мире смайликов, а начиналось все очень просто и незатейливо.

(Сайт freeimg.ru/kartinka/22084)
Развиваясь по спирали, мир вернулся к пиктограммам на новом высоком уровне. Что такое дорожные знаки – это своеобразные пиктограммы, облегчающие ориентацию участникам движения. Готовясь сдавать на водительские права, люди изучают значительное количество таких дорожных знаков.

К пиктограммам люди вернулись не только в переписке в соцсетях, но и в межнациональных связях. С развитием международного общения на транспортных узлах: вокзалах, аэропортах, морских портах в ход пошли пиктограммы, помогающие разноязычным пассажирам ориентироваться в окружающем пространстве.
Вне зависимости от родного языка, грамотный человек не почувствует затруднений в понимании соответствующих пиктограмм, которые все шире возвращаются в нашу жизнь.
Рассмотрим еще одну специфическую область письменности – символы, используемые математиками. Возможно, вы удивитесь, если я скажу, что все мы до сих пор постоянно пользуемся иероглифами, но это действительно так. Причем эта удивительная система иероглифов является международной и одинаково понятна людям множества стран. Символ 1 русский прочитает как один, немец – eins, англичанин – one, эстонец – üks, казах – бiр, но поймут они одно и то же. На разных языках один символ означает целое слово, выражаемое несколькими буквами. Символ, с помощью которого передается целое слово или понятие – это и есть иероглиф, поэтому 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – это международная система иероглифов. Если вас попросят прочитать написанные знаки, они превратятся в слова: ноль, один, два, три, четыре, пять, шесть, семь, восемь, девять или null, eins, zwei, drei, vier, fünf, sechs, sieben, acht, neun и так далее, в зависимости от вашего родного языка. Математики в дополнение к обычным словам письменной речи создали свой иероглифический алфавит, в котором каждый знак означает целое слово, читаемое по-разному на разных языках, но понимаемое одинаково всеми людьми. Кроме уже перечисленных десяти цифр это, например, такие знаки:

читаемые по-русски: равно, меньше, больше, не равно, корень квадратный, корень третьей степени, неопределенный интеграл, определенный интеграл, минус, плюс, умножить, разделить, объединение, пересечение, включение, пустое множество, треугольник, угол, перпендикулярно, бесконечность, модуль вектора, производная, дифференциал, сумма и многие другие.
Задача, поставленная в этой книге – рассказывать о русском языке, проводя аналогии с разделами математики, но, сохраняя приоритет языка, поэтому не будем подробно останавливаться на развитии систем нумерации и возникновении отдельных математических символов-иероглифов. Главное отличие в том, что любой языковый алфавит создавался весь как целостная система знаков, а каждый математический символ вводился по отдельности и не одновременно, а по мере расширения математических знаний и возникновение потребностей в обозначении каких-то объектов, и большинство символов имеют своих авторов. Сама же система математических символов является своего рода международным языком узкого круга специалистов. В связи с этим могу рассказать интересную историю. Мне приходится иногда помогать студентам решать контрольные работы по высшей математике. У преподавателей математического анализа популярен сборник задач под редакцией Б. П. Демидовича, и они часто дают задания из этого сборника. Иногда не получается быстро решить какое-то задание. На помощь пришли вездесущие китайцы. Они издали решебник задач из сборника Демидовича. Сам решебник написан на китайском языке, но математические символы интернациональны. Вот пример одного из таких решений.
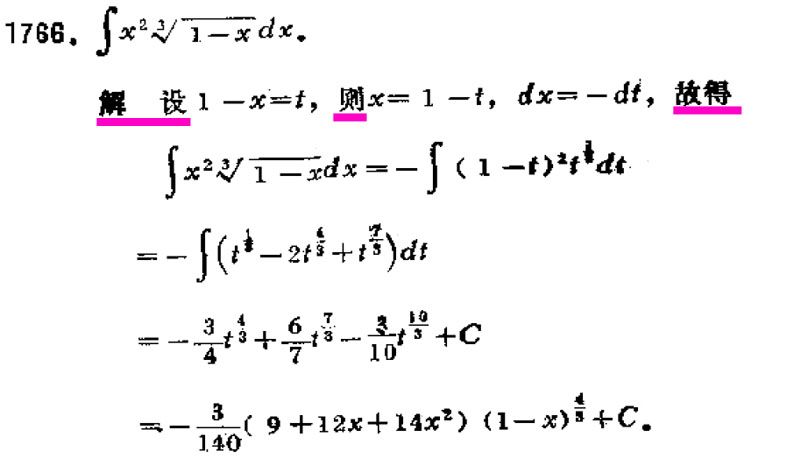
Этот решебник кустарно перепечатывался, поэтому качество печати отвратительное, но разобраться можно. В задании требуется вычислить неопределенный интеграл. Решение содержит всего пять китайских иероглифов, а всё остальное математические знаки и символы. По аналогии с решением других подобных примеров, могу предположить, что первый иероглиф означает «решение», второй – «введем подстановку», третий, «тогда», четвертый и пятый переведу как «получаем выражение». Все остальное переводить не нужно, остается переписать и сказать спасибо китайцам!
Развитие цивилизации не является прямолинейным процессом. Нельзя сказать, что в развитии письменности человечество шло от пиктограмм, иероглифов, к слоговому письму и, наконец, к алфавитам, остановившись на них. Китайцы пока не отказываются от своих иероглифов. Математики для своей специфической области оставили значительное количество иероглифов. В науке вообще оказалось удобно для сокращения количества знаков, использовать некоторые символы. Для химика О – это не только буква о, но это сокращенное обозначение кислорода – химического элемента Oxygenium. Для физика F – это сила, А – работа. Аналогичные процессы происходят и в других науках. Свой иероглифический язык придумали шахматисты для записи шахматных партий – шахматную нотацию.
Шахматная нотация – это система записи течения шахматной партии или определенной позиции на шахматной доске. Без подобной записи трудно было бы накапливать и передавать полезный опыт, учиться шахматному мастерству, совершенствоваться в этой древней интеллектуальной игре. Сейчас принята так называемая алгебраическая нотация. Ее изобрел в XVIII веке сирийский мастер Ф. Стамма и усовершенствовал немецкий шахматист-любитель М. Гиршель. С тех пор она применяется почти без изменений.
Поля шахматной доски обозначаются по горизонтали буквами латинского алфавита – a, b, c, d, e, f, g, h (горизонтальная ось координат), а по вертикали арабскими цифрами – 1, 2, 3, 4, 5, 6, 7, 8 (вертикальная ось координат). Тем самым вводится двумерная или плоская система координат, в которой каждая клетка доски обозначается двумя знаками: латинской буквой, соответствующей вертикальному столбцу и цифрой – соответствующей горизонтальному ряду, на пересечении которых находится данная клетка доски.
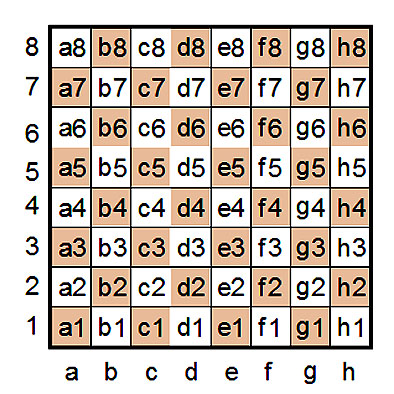
Фигуры обозначаются на русском языке так:
Кр – король, Ф – ферзь, Л – ладья, С – слон,
К – конь, пп – пешки.
Специальные обозначения вводятся для определенных положений на доске:

При записи шахматной партии вначале указывается порядковый номер хода, который отделяется от записи самого хода точкой. После порядкового номера хода и точки указывается обозначение фигуры, делающей ход (кроме пешек), поле, с которого она пошла, и после тире или знака взятия – поле, на которое она пошла. При ходе белых и ответе черных номер хода указывается только для белых, а ход черных записывается в этой же строчке через пробел после хода белых.
Пример записи кратчайшей шахматной партии, которая заканчивается так называемым детским матом:
1. e2 – e4 e7 – e5
2. Cf1 – c4 Кb8 – c6
3. Фd1 – h5 Кg8 – f6??
4. Фh5:f7х.
Шахматная запись интересна тем, что она интернациональна. На других языках изменятся только обозначения фигур? Например, на немецком языке будет следующее обозначение фигур:
K – (König) король, D – (Dame) ферзь,
T – (Turm) ладья, L – (Läufer) слон,
S – (Springer) конь, B – (Bauer) пешки.
Еще более интересную и своеобразную письменность создали музыканты. Запись музыки, как и шахматная нотация интернациональна. Музыкант берет в руки нотную тетрадь и читает её, так же как простые люди читают книгу. Знаки нот у него в голове превращаются в звуки и мелодию, которые он слышит. Обучаясь в детстве играть на фортепиано, я так и не усвоил эту премудрость. То ли слух музыкальный недостаточно развит, то ли мало занимался, но с нотного листа музыку не слышу. Мне нужно проиграть на инструменте, чтобы понять мелодию.
В мире так много интересного, что меня постоянно уводит в сторону от русского языка и математики. Оправданием служит только то, что мы все-таки остаемся в русле развития письменности, ведь и математически символы и шахматная нотация и музыкальная грамота – всё это её величество письменность в разных своих проявлениях. Кроме того широта кругозора никому не повредит. Чем больше человек знает, тем более он интересен окружающим людям в общении.
Симметрия
Поставьте перед собой на столе зеркало, положите перед ним лист бумаги и напишите большими печатными буквами слова КОФЕ и ЧАЙ. Взглянув в зеркало, вы увидите, что отражение слова КОФЕ сохранило свое начертание, а буквы слова ЧАЙ перевернулись. Почему так получилось? Дело в том, что слово КОФЕ тоже перевернулось, но его буквы симметричны относительно горизонтальной оси, и их начертание в зеркале не изменяется. Эксперимент наводит на мысль о необходимости рассмотреть подробно понятие симметрии применительно к буквам и словам русского языка, на этом пути открывается много интересного.
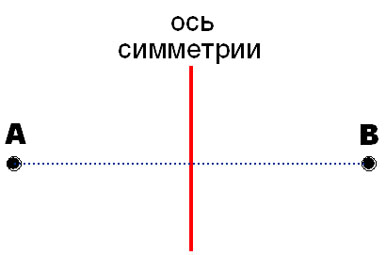
Две точки, лежащие на одном перпендикуляре к данной прямой по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно этой прямой.
Точки А и В называются симметричными относительно оси. Плоская фигура симметрична относительно прямой (оси симметрии), если ее точки попарно обладают указанным свойством.
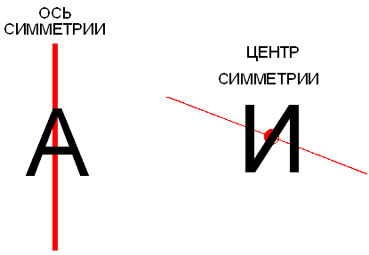
Фигура симметрична относительно точки (центра симметрии), если её точки попарно лежат на прямых проходящих через центр, по разные стороны и на равных расстояниях от него.
Симметрия не только математическое понятие. Она присутствует во множестве предметов и явлений окружающего мира. Противоположным понятием является асимметрия (отсутствие симметрии). Их взаимодействие проявляется, в частности, в строении человеческого тела: при внешней его симметрии (ноги, руки, уши, глаза) основные внутренние органы (сердце, печень, желудок) не симметричны. Надо же было так придумать!
Применительно к буквам и словам, как графическим изображениям будем рассматривать три вида симметрии: симметрия относительно горизонтальной оси, симметрия относительно вертикальной оси и центральная симметрия. Для изображения букв существуют различные шрифты, отличающиеся друг от друга декоративными элементами. Условимся не брать это во внимание и рассматривать самый простейший вариант написания букв. В некоторых буквах верхние элементы изображаются несколько меньше нижних (В, Е, З, Н, Х, Э) или графически немного изменены (Ж, К) – это различие мы тоже будем игнорировать. В результате за основу можно взять шрифт Arial, отредактировав в сторону упрощения буквы Д и Л.

