Illustrations of Universal Progress: A Series of Discussions

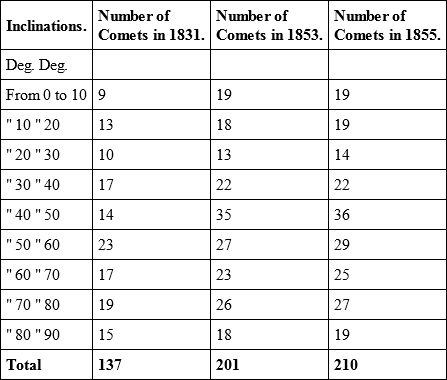
At first sight this table seems not to warrant our statement. Assuming the alleged general relation between the inclinations of cometary orbits, and the directions in space from which the comets come, the table may be thought to show that the frequency of comets increases as we progress from the plane of the ecliptic up to 45°, and then decreases up to 90°. But this apparent diminution arises from the fact that the successive zones of space rapidly diminish in their areas on approaching the poles. If we allow for this, we shall find that the excess of comets continues to increase up to the highest angles of inclination. In the table below, which, for convenience, is arranged in inverted order, we have taken as standards of comparison the area of the zone round the pole, and the number of comets it contains; and having ascertained the areas of the other zones, and the numbers of comets they should contain were comets equally distributed, we have shown how great becomes the deficiency in descending from the poles of the ecliptic to its plane.

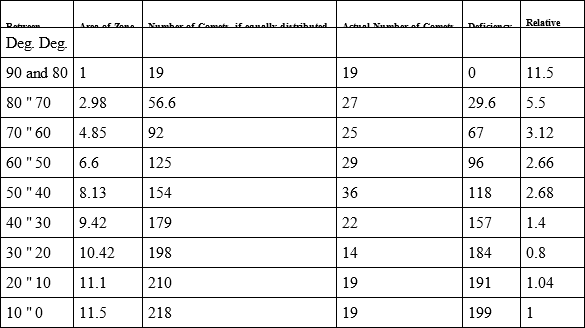
In strictness, the calculation should be made with reference, not to the plane of the ecliptic, but to the plane of the sun's equator; and this might or might not render the progression more regular. Probably, too, the progression would be made somewhat different were the calculation based, as it should be, not on the inclinations of orbit-planes, but on the inclinations of major axes. But even as it is, the result is sufficiently significant: since, though the conclusion that comets are 11·5 times more abundant about the poles of the ecliptic than about its plane, can be but a rough approximation to the truth, yet no correction of it is likely very much to change this strong contrast.

What, then, is the meaning of this fact? It has several meanings. It negatives the supposition, favoured by Laplace among others, that comets are bodies that were wandering in space, or have come from other systems; for the probabilities are infinity to one against the orbits of such wandering bodies showing any definite relation to the plane of the Solar System. For the like reason, it negatives the hypothesis of Lagrange, otherwise objectionable, that comets have resulted from planetary catastrophes analogous to that which is supposed to have produced the asteroids. It clearly shows that, instead of comets being accidental members of the Solar System, they are necessary members of it – have as distinct a structural relation to it as the planets themselves. That comets are abundant round the axis of the Solar System, and grow rarer as we approach its plane, implies that the genesis of comets has followed some law– a law in some way concerned with the genesis of the Solar System.

If we ask for any so-called final cause of this arrangement, none can be assigned: until a probable use for comets has been shown, no reason can be given why they should be thus distributed. But when we consider the question as one of physical science, we see that comets are antithetical to planets, not only in their great rarity, in their motions as indifferently direct or retrograde, in their eccentric orbits, and in the varied directions of those orbits; but we see the antithesis further marked in this, that while planets have some relation to the plane of nebular rotation, comets have some relation to the axis of nebular rotation.11 And without attempting to explain the nature of this relation, the mere fact that such a relation exists, indicates that comets have resulted from a process of evolution – points to a past time when the matter now forming the Solar System extended to those distant regions of space which comets visit.

See, then, how differently this class of phenomena bears on the antagonistic hypotheses. To the hypothesis commonly received, comets are stumbling-blocks: why there should be hundreds (or probably thousands) of extremely rare aeriform masses rushing to and fro round the sun, it cannot say; any more than it can explain their physical constitutions, their various and eccentric movements, or their distribution. The hypothesis of evolution, on the other hand, not only allows of the general answer, that they are minor results of the genetic process; but also furnishes us with something like explanations of their several peculiarities.

And now, leaving these erratic bodies, let us turn to the more familiar and important members of the Solar System. It was the remarkable harmony subsisting among their movements, which first made Laplace conceive that the sun, planets, and satellites had resulted from a common genetic process. As Sir William Herschel, by his observations on the nebulæ, was led to the conclusion that stars resulted from the aggregation of diffused matter; so Laplace, by his observations on the structure of the Solar System, was led to the conclusion that only by the rotation of aggregating matter were its peculiarities to be explained. In his "Exposition du Système du Monde," he enumerates as the leading evidences of evolution: – 1. The movements of the planets in the same direction and almost in the same plane; 2. The movements of the satellites in the same direction as those of the planets; 3. The movement of rotation of these various bodies and of the sun in the same direction as the orbitual motions, and in planes little different; 4. The small eccentricity of the orbits of the planets and satellites, as contrasted with the great eccentricity of the cometary orbits. And the probability that these harmonious movements had a common cause, he calculates as two hundred thousand billions to one.

Observe that this immense preponderance of probability does not point to a common cause under the form ordinarily conceived – an Invisible Power working after the method of "a Great Artificer;" but to an Invisible Power working after the method of evolution. For though the supporters of the common hypothesis may argue that it was necessary for the sake of stability that the planets should go round the sun in the same direction and nearly in one plane, they cannot thus account for the direction of the axial motions. The mechanical equilibrium would not have been at all interfered with, had the sun been without any rotatory movement; or had he revolved on his axis in a direction opposite to that in which the planets go round him; or in a direction at right angles to the plane of their orbits. With equal safety the motion of the Moon round the Earth might have been the reverse of the Earth's motion round its axis; or the motion of Jupiter's satellites might similarly have been at variance with his axial motion; or that of Saturn's satellites with his. As, however, none of these alternatives have been followed, the uniformity must be considered, in this case as in all others, evidence of subordination to some general law – implies what we call natural causation, as distinguished from arbitrary arrangement.

Hence the hypothesis of evolution would be the only probable one, even in the absence of any clue to the particular mode of evolution. But when we have, propounded by a mathematician whose authority is second to none, a definite theory of this evolution based on established mechanical laws, which accounts for these various peculiarities, as well as for many minor ones, the conclusion that the Solar System was evolved becomes almost irresistible.

The general nature of Laplace's theory scarcely needs stating. Books of popular astronomy have familiarized most readers with his conceptions; – namely, that the matter now condensed into the Solar System, once formed a vast rotating spheroid of extreme rarity extending beyond the orbit of Neptune; that as this spheroid contracted, its rate of rotation necessarily increased; that by augmenting centrifugal force its equatorial zone was from time to time prevented from following any further the concentrating mass, and so remained behind as a revolving ring; that each of the revolving rings thus periodically detached, eventually became ruptured at its weakest point, and contracting on itself, gradually aggregated into a rotating mass; that this, like the parent mass, increased in rapidity of rotation as it decreased in size, and, where the centrifugal force was sufficient, similarly threw off rings, which finally collapsed into rotating spheroids; and that thus out of these primary and secondary rings there arose planets and their satellites, while from the central mass there resulted the sun. Moreover, it is tolerably well known that this à priori reasoning harmonizes with the results of experiment. Dr. Plateau has shown that when a mass of fluid is, as far may be, protected from the action of external forces, it will, if made to rotate with adequate velocity, form detached rings; and that these rings will break up into spheroids which turn on their axes in the same direction with the central mass. Thus, given the original nebula, which, acquiring a vortical motion in the way we have explained, has at length concentrated into a vast spheroid of aeriform matter moving round its axis – given this, and mechanical principles explain the rest. The genesis of a solar system displaying movements like those observed, may be predicted; and the reasoning on which the prediction is based is countenanced by experiment.12

But now let us inquire whether, besides these most conspicuous peculiarities of the Solar System, sundry minor ones are not similarly explicable. Take first the relation between the planes of the planetary orbits and the plane of the sun's equator. If, when the nebulous spheroid extended beyond the orbit of Neptune, all parts of it had been revolving exactly in the same plane or rather in parallel planes – if all its parts had had one axis; then the planes of the successive rings would have been coincident with each other and with that of the sun's rotation. But it needs only to go back to the earlier stages of concentration, to see that there could exist no such complete uniformity of motion. The flocculi, already described as precipitated from an irregular and widely-diffused nebula, and as starting from all points to their common centre of gravity, must move not in one plane but in innumerable planes, cutting each other at all angles.

The gradual establishment of a vortical motion such as we saw must eventually arise, and such as we at present see indicated in the spiral nebulæ, is the gradual approach toward motion in one plane – the plane of greatest momentum. But this plane can only slowly become decided. Flocculi not moving in this plane, but entering into the aggregation at various inclinations, will tend to perform their revolutions round its centre in their own planes; and only in course of time will their motions be partly destroyed by conflicting ones, and partly resolved into the general motion. Especially will the outermost portions of the rotating mass retain for long time their more or less independent directions; seeing that neither by friction nor by the central forces will they be so much restrained. Hence the probabilities are, that the planes of the rings first detached will differ considerably from the average plane of the mass; while the planes of those detached latest will differ from it less. Here, again, inference to a considerable extent agrees with observation. Though the progression is irregular, yet on the average the inclinations decrease on approaching the sun.

Consider next the movements of the planets on their axes. Laplace alleged as one among other evidences of a common genetic cause, that the planets rotate in a direction the same as that in which they go round the sun, and on axes approximately perpendicular to their orbits. Since he wrote, an exception to this general rule has been discovered in the case of Uranus, and another still more recently in the case of Neptune – judging, at least, from the motions of their respective satellites. This anomaly has been thought to throw considerable doubt on his speculation; and at first sight it does so. But a little reflection will, we believe, show that the anomaly is by no means an insoluble one; and that Laplace simply went too far in putting down as a certain result of nebular genesis, what is, in some instances, only a probable result. The cause he pointed out as determining the direction of rotation, is the greater absolute velocity of the outer part of the detached ring. But there are conditions under which this difference of velocity may be relatively insignificant, even if it exists: and others in which, though existing to a considerable extent, it will not suffice to determine the direction of rotation.

Note, in the first place, that in virtue of their origin, the different strata of a concentrating nebulous spheroid, will be very unlikely to move with equal angular velocities: only by friction continued for an indefinite time will their angular velocities be made uniform; and especially will the outermost strata, for reasons just now assigned, maintain for the longest time their differences of movement. Hence, it is possible that in the rings first detached the outer rims may not have greater absolute velocities; and thus the resulting planets may have retrograde rotations. Again, the sectional form of the ring is a circumstance of moment; and this form must have differed more or less in every case. To make this clear, some illustration will be necessary. Suppose we take an orange, and assuming the marks of the stalk and the calyx to represent the poles, cut off round the line of the equator a strip of peel. This strip of peel, if placed on the table with its ends meeting, will make a ring shaped like the hoop of a barrel – a ring whose thickness in the line of its diameter is very small, but whose width in a direction perpendicular to its diameter is considerable. Suppose, now, that in place of an orange, which is a spheroid of very slight oblateness, we take a spheroid of very great oblateness, shaped somewhat like a lens of small convexity. If from the edge or equator of this lens-shaped spheroid, a ring of moderate size were cut off, it would be unlike the previous ring in this respect, that its greatest thickness would be in the line of its diameter, and not in a line at right angles to its diameter: it would be a ring shaped somewhat like a quoit, only far more slender. That is to say, according to the oblateness of a rotating spheroid, the detached ring may be either a hoop-shaped ring or a quoit-shaped ring.

One further fact must be noted. In a much-flattened or lens-shaped spheroid, the form of the ring will vary with its bulk. A very slender ring, taking off just the equatorial surface, will be hoop-shaped; while a tolerably massive ring, trenching appreciably on the diameter of the spheroid, will be quoit-shaped. Thus, then, according to the oblateness of the spheroid and the bulkiness of the detached ring, will the greatest thickness of that ring be in the direction of its plane, or in a direction perpendicular to its plane. But this circumstance must greatly affect the rotation of the resulting planet. In a decidedly hoop-shaped nebulous ring, the differences of velocity between the inner and outer surfaces will be very small; and such a ring, aggregating into a mass whose greatest diameter is at right angles to the plane of the orbit, will almost certainly give to this mass a predominant tendency to rotate in a direction at right angles to the plane of the orbit. Where the ring is but little hoop-shaped, and the difference of the inner and outer velocities also greater, as it must be, the opposing tendencies – one to produce rotation in the plane of the orbit, and the other rotation perpendicular to it – will both be influential; and an intermediate plane of rotation will be taken up. While, if the nebulous ring is decidedly quoit-shaped, and therefore aggregates into a mass whose greatest dimension lies in the plane of the orbit, both tendencies will conspire to produce rotation in that plane.

On referring to the facts, we find them, as far as can be judged, in harmony with this view. Considering the enormous circumference of Uranus's orbit, and his comparatively small mass, we may conclude that the ring from which he resulted was a comparatively slender, and therefore a hoop-shaped one: especially if the nebulous mass was at that time less oblate than afterwards, which it must have been. Hence, a plane of rotation nearly perpendicular to his orbit, and a direction of rotation having no reference to his orbitual movement. Saturn has a mass seven times as great, and an orbit of less than half the diameter; whence it follows that his genetic ring, having less than half the circumference, and less than half the vertical thickness (the spheroid being then certainly as oblate, and indeed more oblate), must have had considerably greater width – must have been less hoop-shaped, and more approaching to the quoit-shaped: notwithstanding difference of density, it must have been at least two or three times as broad in the line of its plane. Consequently, Saturn has a rotatory movement in the same direction as the movement of translation, and in a plane differing from it by thirty degrees only.

In the case of Jupiter, again, whose mass is three and a half times that of Saturn, and whose orbit is little more than half the size, the genetic ring must, for the like reasons, have been still broader – decidedly quoit-shaped, we may say; and there hence resulted a planet whose plane of rotation differs from that of his orbit by scarcely more than three degrees. Once more, considering the comparative insignificance of Mars, Earth, Venus, and Mercury, it follows that the diminishing circumferences of the rings not sufficing to account for the smallness of the resulting masses, the rings must have been slender ones – must have again approximated to the hoop-shaped; and thus it happens that the planes of rotation again diverge more or less widely from those of the orbits. Taking into account the increasing oblateness of the original spheroid in the successive stages of its concentration, and the different proportions of the detached rings, it seems to us that the respective rotatory motions are not at variance with the hypothesis.

Not only the directions, but also the velocities of rotation are thus explicable. It might naturally be supposed that the large planets would revolve on their axes more slowly than the small ones: our terrestrial experiences incline us to expect this. It is a corollary from the Nebular Hypothesis, however, more especially when interpreted as above, that while large planets will rotate rapidly, small ones will rotate slowly; and we find that in fact they do so. Other things equal, a concentrating nebulous mass that is diffused through a wide space, and whose outer parts have, therefore, to travel from great distances to the common centre of gravity, will acquire a high axial velocity in course of its aggregation: and conversely with a small mass. Still more marked will be the difference where the form of the genetic ring conspires to increase the rate of rotation. Other things equal, a genetic ring that is broadest in the direction of its plane will produce a mass rotating faster than one that is broadest at right angles to its plane; and if the ring is absolutely as well as relatively broad, the rotation will be very rapid. These conditions were, as we saw, fulfilled in the case of Jupiter; and Jupiter goes round his axis in less than ten hours. Saturn, in whose case, as above explained, the conditions were less favourable to rapid rotation, takes ten hours and a half. While Mars, Earth, Venus, and Mercury, whose rings must have been slender, take more than double the time: the smallest taking the longest.

From the planets, let us now pass to the satellites. Here, beyond the conspicuous facts commonly adverted to, that they go round their primaries in the same directions that these turn on their axes, in planes diverging but little from their equators, and in orbits nearly circular, there are several significant traits which must not be passed over.

One of them is, that each set of satellites repeats in miniature the relations of the planets to the sun, both in the respects just named, and in the order of the sizes. On progressing from the outside of the Solar System to its centre, we see that there are four large external planets, and four internal ones which are comparatively small. A like contrast holds between the outer and inner satellites in every case. Among the four satellites of Jupiter, the parallel is maintained as well as the comparative smallness of the number allows: the two outer ones are the largest, and the two inner ones the smallest. According to the most recent observations made by Mr. Lassell, the like is true of the four satellites of Uranus. In the case of Saturn, who has eight secondary planets revolving round him, the likeness is still more close in arrangement as in number: the three outer satellites are large, the inner ones small; and the contrasts of size are here much greater between the largest, which is nearly as big as Mars, and the smallest, which is with difficulty discovered even by the best telescopes.

Moreover, the analogy does not end here. Just as with the planets, there is at first a general increase of size on travelling inwards from Neptune and Uranus, which do not differ very widely, to Saturn, which is much larger, and to Jupiter, which is the largest; so of the eight satellites of Saturn, the largest is not the outermost, but the outermost save two; so of Jupiter's four secondaries, the largest is the most remote but one. Now these analogies are inexplicable by the theory of final causes. For purposes of lighting, if this be the presumed object of these attendant bodies, it would have been far better had the larger been the nearer: at present, their remoteness renders them of less service than the smallest. To the Nebular Hypothesis, however, these analogies give further support. They show the action of a common physical cause. They imply a law of genesis, holding in the secondary systems as in the primary system.

Still more instructive shall we find the distribution of the satellites – their absence in some instances, and their presence in other instances, in smaller or greater numbers. The argument from design fails to account for this distribution. Supposing it be granted that planets nearer the Sun than ourselves, have no need of moons (though, considering that their nights are as dark, and, relatively to their brilliant days, even darker than ours, the need seems quite as great) – supposing this to be granted; what is to be said of Mars, which, placed half as far again from the Sun as we are, has yet no moon? Or again, how are we to explain the fact that Uranus has but half as many moons as Saturn, though he is at double the distance? While, however, the current presumption is untenable, the Nebular Hypothesis furnishes us with an explanation. It actually enables us to predict, by a not very complex calculation, where satellites will be abundant and where they will be absent. The reasoning is as follows.

In a rotating nebulous spheroid that is concentrating into a planet, there are at work two antagonist mechanical tendencies – the centripetal and the centrifugal. While the force of gravitation draws all the atoms of the spheroid together, their tangential momentum is resolvable into two parts, of which one resists gravitation. The ratio which this centrifugal force bears to gravitation, varies, other things equal, as the square of the velocity. Hence, the aggregation of a rotating nebulous spheroid will be more or less strongly opposed by this outward impetus of its particles, according as its rate of rotation is high or low: the opposition, in equal spheroids, being four times as great when the rotation is twice as rapid; nine times as great when it is three times as rapid; and so on. Now, the detachment of a ring from a planet-forming body of nebulous matter, implies that at its equatorial zone the centrifugal force produced by concentration has become so great as to balance gravity. Whence it is tolerably obvious that the detachment of rings will be most frequent from those masses in which the centrifugal tendency bears the greatest ratio to the gravitative tendency. Though it is not possible to calculate what proportions these two tendencies had to each other in the genetic spheroid which produced each planet; it is possible to calculate where each was the greatest and where the least. While it is true that the ratio which centrifugal force now bears to gravity at the equator of each planet, differs widely from that which it bore during the earlier stages of concentration; and while it is true that this change in the ratio, depending on the degree of contraction each planet has undergone, has in no two cases been the same; yet we may fairly conclude that where the ratio is still the greatest, it has been the greatest from the beginning. The satellite-forming tendency which each planet had, will be approximately indicated by the proportion now existing in it between the aggregating power, and the power that has opposed aggregation. On making the requisite calculations, a remarkable harmony with this inference comes out. The following table shows what fraction the centrifugal force is of the centripetal force in every case; and the relation which that fraction bears to the number of satellites.