
Полная версия:
Математические модели в естественнонаучном образовании. Том I
% Выход: mat = бифукационная матрица размера N на L
% которая хранит последовательность длины L
% для каждой пары (x0, параметр a)
% –
% установки по умолчанию
if ~exist('p_siz','var')
p_siz = 1;
end
% инициализация
mat = zeros(N,L);
a = linspace(a0,a1,N);
% основной цикл
format long
for i = 1:N
ca = a(i); % выбрать одно значение параметра в каждый момент времени
for j = 1:L % сгенерировать последовательность длиной L
if j == 1
pre = x0; % инициализируем стартовое значение
for k = 1:preL % пропускаем значения переходного процесса
nxt = fun(pre,ca);
pre = nxt;
end
end
nxt = fun(pre,ca); % вычисляем следующее значение последовательности
mat(i,j) = nxt; % сохраняем в результирующей матрице mat
pre = nxt; % последнее значение будет начальным для следующей итерации
end
end
% построение графика
dcolor = [0,0,1]; % настройка цвета маркера: синий
[r,c] = meshgrid(1:L,a); % наполяем сетку данных координат
surf(r,c,mat,'Marker','*','MarkerSize',p_siz,'FaceColor','None','MarkerEdgeColor', dcolor,'EdgeColor','None')
view([90,0,0]) % фиксируем направление камеры
ylim([a0,a1]) % размещаем данные на диаграмме
end
2. Для популяции со временем регенерации значительно меньшей единицы времени может быть неуместно думать о пропускной способности как о константе. Исследуйте, что произойдет, если пропускная способность изменяется синусоидально. Для начала попробуйте понять следующие команды MATLAB:
t=[0:50]
K=5+sin((2*pi/12)*t)
p=.1; pops=p
for i=1:50
p=p+.2*p*(1-p/K(i));
pops=[pops p];
end
plot(t,K,t,pops)
Рекомендации
Объясните, почему синусоидально изменяющаяся пропускная способность может иметь физический или социально-экономический смысл при некоторых обстоятельствах.
Исследуйте поведение модели для различных вариантов
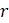
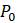
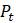
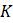
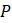
Что происходит, если изменяется частота колебаний пропускной способности? Попробуйте заменить
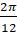
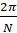
По мере увеличения
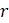
3. Изучите, что произойдет, если пропускная способность изменяется случайным образом в логистической модели, и, в частности, влияние такой пропускная способность на небольшие популяции. Нужно будет знать, что команда rand(1) в MATLAB выдает случайное число в диапазоне от 0 до 1 с равномерным распределением, и что randn(1) генерирует случайное число из нормального распределения с матожиданием 0 и стандартным отклонением 1. Можете начать с использования программы onepop.m с выражением типа 10 + rand(1) в качестве пропускной способности в логистической модели.
Рекомендации
Возможно, 10*rand(1) или 10+2*randn(1) были бы лучшей формулой для значений
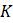
Для выбранного выражения изучите поведение модели для различных вариантов
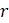
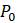
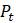
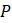
По мере увеличения
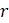
Исследуйте, что происходит, если численность популяции небольшая и принимает целые значения. В MATLAB команда floor(p) возвращает ближайшее целое число меньше или равное
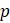
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Вы ознакомились с фрагментом книги.
Для бесплатного чтения открыта только часть текста.
Приобретайте полный текст книги у нашего партнера:
Полная версия книги
Всего 10 форматов



