
Полная версия:
Математические модели в естественнонаучном образовании. Том I

Денис Соломатин
Математические модели в естественнонаучном образовании. Том I
Доброй памяти Л.М.Мартынова, величайшего алгебраиста и криптографа современности, посвящается.
Предисловие
Связь между техническими и гуманитарными науками становится всё теснее. Классические задачи, такие как моделирование популяций и заболеваний, сменяются новыми проблемами моделирования машинного обучения, усложняющимися по мере накопления эмпирических данных, и вновь делают математику перспективной сферой человеческой деятельности. Не секрет, что естественный интеллект на сегодняшний день превосходит искусственного лишь эмоциональной составляющей и математической интуицией. Именно поэтому предполагается, что данная сфера будет по-прежнему одной из самых быстрорастущих.
Мы считаем, что межпредметные связи должны проявляться на всех уровнях математического образования. Студенты-математики получают определённый опыт и несомненную пользу, наблюдая приложения математики из неожиданных областей, открытых для них, извлекают выгоду из изучения того, как математические инструменты могут помочь им реализовать свои собственные проекты. Образ дидактики как нематематической науки, который сохраняется среди многих студентов педагогических колледжей, оказывает медвежью услугу тем, кто придерживается такой точки зрения. Настоящая монография является попыткой представить некоторые существенные темы математического моделирования на принципиально новом языке, адаптированном к математическому образованию. Надеемся, что это может мотивировать некоторых студентов-математиков педагогических специальностей продолжать свои математические исследования за пределами традиционного уровня. Такие студенты, как правило, имеют сильный интерес к математике и базовую математическую подготовку, достаточную для самостоятельного изучения её приложений. Таким образом, мы не предполагаем никакой дополнительной подготовки в области высшей математики за пределами классического курса; моделирование с помощью разностных уравнений позволяет свести к минимуму предварительную подготовку. Математические темы, обычно изучаемые на факультативных курсах, вводятся по мере необходимости для моделирования и последующего анализа полученных моделей. Несмотря на такой план изложения, мы знаем, что многие студенты изучают курс высшей математики и, возможно, другие специализированные курсы. Поэтому без колебаний включим вопросы для самопроверки и задачи для самостоятельного решения (они выделены курсивом отдельно), которые могут пригодиться тем, у кого есть дополнительная математическая подготовка. По нашему опыту работы в группах физико-математического профиля, студенты с фундаментальным образованием нашли для себя здесь много нового. Большая часть материала также апеллирует к знаниям студентов и по другим дисциплинам, которые просто интересны и занимательны сами по себе. Следовательно, монография может быть продуктивно использована как для проведения аудиторных занятий, так и для самостоятельного изучения на разных уровнях.
Нет уверенности в том, что к моменту издания будут охвачены все передовые направления столь бурно развивающейся отрасли, но стоит предположить, как поверхностное освещение какой-либо случайной темы вдохновит студентов на самостоятельное погружение в заинтересовавшую их область. В частности, когда вводятся некоторые модели, оставляем их анализ в качестве упражнений. Хотя подобное нельзя считать эффективным способом энциклопедичного изложения материала, мы надеемся, что это приведет к более глубокому пониманию изучаемого.
Поскольку компьютерные эксперименты с моделями бывают достаточно информативными, текст насыщен сериями программ. Простой интерфейс MATLAB, его широкая доступность как в профессиональной, так и в студенческой версиях, поддержка числовых и символьных вычислений, позволяет минимизировать усилия, затрачиваемые на решение типовых задач математического моделирования. Хотя компьютер и является инструментом, которым студенты должны уметь пользоваться, его использование ни в коем случае не является панацеей.
В дополнение к многочисленным упражнениям в монографии представлены различные проектные работы. Предлагается тема исследования и некоторые способы ее изучения, но все они, по крайней мере на данный момент, являются частично открытыми математическими проблемами. Кроме того, что это позволяет студентам работать на разных уровнях сложности, это прививает навыки реальной математической и научной работы.
По всему тексту разбросаны контрольные вопросы, помеченные знаком «?». Они предназначены для дополнительного стимулирования сознания и предотвращения пассивного чтения. Ответы окажутся вполне очевидными после небольшого самостоятельного размышления, либо соответствующий вопрос будет обсуждаться в тексте позднее. Если находите такие вопросы раздражающими, пожалуйста, не стесняйтесь игнорировать их.
В тексте больше фактического материала, чем можно было бы охватить за полноценный семестр, предлагая преподавателям множество вариантов изучения тем. Например, темы глав 1, 2, 3 и 7, пожалуй, являются наиболее привычными для академического курса математического моделирования и уравнения математической физики, охватывающие классические модели, как линейные, так и нелинейные. Главы 4 и 5 предлагают студентам введение в новые темы эволюционного моделирования и построения дерева решений, которые являются перспективными и полезными при построениях различных классификаторов. Глава 6, посвященная генетическим алгоритмам, дает представление о другой области, в которой математика и биология оказались тесно переплетены, вдохновляясь идеями друг от друга. Глава 8 и Приложение содержат краткое введение в основные инструменты подгонки кривых и статистики.
В главе 1 вводится понятия динамического моделирования с помощью разностных уравнений от одной переменной, включая ключевые понятия равновесия, линеаризации и стабильности. В главе 2 эксплуатируем матричную алгебру, вычисление собственных чисел и векторов, с помощью линейных моделей от двух переменных. Эти главы являются основой для изложения всего последующего материала.
Экскурс в теорию вероятностей появляется в двух разделах главы 4, чтобы смоделировать эволюционное развитие математического образования, а затем расширяется в главе 6 на применение генетических алгоритмов. Глава 5, которая имеет алгоритмический привкус, отличный от остальной части текста, частично зависит от формул расстояния, полученных в главе 4. Трактовка моделей в главе 8, естественным образом зависит от введённой в главе 3 модели взаимодействующих факторов.
Разработка этой монографии началась давно, в течение нескольких лет появлялись краткие версии нескольких глав. После многих дополнительных пересмотров конспекты курса достигли критической массы, и публикация их для использования другими преподавателями оказалась лишь вопросом времени.
Многие студенты помогали, как в качестве критиков, так и в качестве экспериментаторов, пытаясь решать предлагаемые задачи, вычитывая текст, задавая много вопросов. Несмотря на все старания, некоторые ошибки наверняка просочились, пожалуйста, сообщите автору обо всем, что сочтёте неверным.
Многие из упражнений и проектов относятся к компьютерному математическому пакету MATLAB. Изучение базовых команд этого пакета для использования его в качестве мощного калькулятора является простым и полезным делом. Когда потребуются более сложные команды для решения упражнений, примеры обычно будут приводиться в постановках задач. Таким образом модели будут постепенно усложняется с применением специализированного программного обеспечения.
MATLAB по сути является полноценным языком программирования с отличными графическими возможностями. Мы воспользовались этими функциями, чтобы предоставить несколько программ, упрощая изучение математических моделей для начинающих. В упражнениях и проектах используются некоторые программы и файлы данных, приводимые ниже.
Готовые тексты программ приводятся в целях минимизации необходимого багажа знаний синтаксиса MATLAB. Чтобы запустить большинство программ ниже, просто скопируйте их из электронного варианта книги или введите в окне редактора скриптов MATLAB.
Можно просто сохранить текст программы в файл с расширением m. Для запуска такого скрипта в окне водится имя запускаемого файла. После запуска будет задан ряд вопросов о конструируемых моделях и их параметрах. Команда help имя_файла также предоставляет краткое описание функций программы, получаемое из комментариев в первых строках программы. Поскольку m-файлы являются текстовыми файлами, они могут быть прочитаны и изменены любым заинтересованным пользователем.
Некоторые m-файлы определяют функции, которые принимают аргументы. Например, такая команда, как compseq(seq1,seq2), запускает программу compseq.m для сравнения двух последовательностей ДНК seq1 и seq2. Набрав help compseq, можно увидеть объяснение синтаксиса такой функции. A mat-файл содержит данные, доступ к которым возможен только из MATLAB. Чтобы загрузить такой файл, скажем, seqdata.mat, введите load seqdata. Имена всех новых переменных, которые будут созданы, можно увидеть вводя команду who, в то время как значения, хранящиеся в этих переменных, можно увидеть просто вводя имя переменной.
Некоторые файлы данных могут быть предоставлены в виде m-файлов, тогда вспомогательные комментарии и пояснения сохраняются вместе с данными. Для них запуск m-файла создает переменные, так же, как и загрузка mat-файла. Комментарии можно прочитать с помощью любого текстового редактора.
В ходе выполнения задач для самостоятельного решения предлагается использовать следующие файлы скриптов MATLAB, доступных из открытых источников:
aidsdata.m – содержит данные числа случаев синдрома приобретенного иммунодефицита;
cobweb.m и cobweb2.m – рисуют графики с паутинной диаграммой для итераций модели с одной популяцией; первая программа оставляет все рисуемые линии, а вторая программа постепенно стирает их;
compseq.m – функция сравнивает две последовательности ДНК, получая частотную таблицу количества фрагментов с каждой из возможных базовых комбинаций;
distances.m – функция вычисляет расстояния Джукса-Кантора, 2-параметрическое расстояние Кимуры и логарифмическое расстояния между всеми парами в коллекции последовательностей ДНК;
distJC.m, distK2.m и distLD.m – функции вычисляют расстояние Джукса-Кантора, 2-параметрическое расстояние Кимуры и логарифмическое расстояние для одной пары последовательностей, описываемых частотным массивом сайтов ДНК с каждой комбинацией оснований;
flhivdata.m – содержит последовательности ДНК гена оболочки вируса иммунодефицита человека из «случая стоматолога во Флориде»;
genemap.m – моделирует данные тестового скрещивания для проекта генетического картирования, используя гены мухи или мыши;
genesim.m – производит временной график частоты аллелей гена в популяции фиксированного размера; относительные значения приспособленности для генотипов могут быть установлены для моделирования естественного отбора;
informative.m – функция находит участки в выровненных последовательностях ДНК, которые информативны для метода максимальной экономии;
longterm.m – рисует диаграмму бифуркации для модели с одной популяцией, показывая долгосрочное поведение по мере изменения значения одного параметра;
markovJC.m и markovK2.m – эти функции осуществляют получение марковской матрицы Джукса-Кантора или 2-параметрической модели Кимуры с заданными значениями параметров;
mutate.m и mutatef.m – моделирует мутации последовательности ДНК по марковской модели замещения оснований; вторая программа является функциональной версией первой;
nj.m – функция реализует алгоритм присоединения соседей для построения дерева из массива расстояний;
onepop.m – отображает графики итераций модели с одной популяцией;
primatedata.m – содержит последовательности митохондриальной ДНК из 12 приматов, а также вычисленные расстояния между ними;
seqdata.mat – содержит смоделированные данные последовательности ДНК;
seqgen.m – функция генерирует последовательности ДНК с заданной длиной и распределением оснований;
sir.m – отображает итерации эпидемиологической модели SIR, включая графики временной и фазовой плоскости;
twopop.m – отображает итерации 2-популяционной модели, включая графики временной и фазовой плоскости.
Глава 1. Динамическое моделирование разностными уравнениями
Независимо от того, исследуем ли мы рост числа выпускников математических специальностей, взаимодействие с работодателями, эволюцию рабочих программ классических курсов, передачу фундаментальных идей или распространение фейков, дидактические системы характеризуются изменениями и адаптацией. Даже когда они кажутся постоянными и стабильными, это часто является результатом баланса тенденций, толкающих системы в разных направлениях. Большое количество взаимодействий и конкурирующих тенденций может затруднить просмотр полной картины сразу.
Как мы можем понять такие сложные системы, как те, которые возникают в социальных науках? Как мы можем проверить, достаточно ли нашего предполагаемого понимания ключевых процессов, чтобы описать, как ведет себя система? Математический язык предназначен для точного описания, и поэтому описание сложных систем часто требует математической модели.
В этой главе мы рассмотрим некоторые способы, которыми математика используется для моделирования динамических процессов в обучении математике. Простые формулы связывают, например, количество абитуриентов в определенном году с выпускниками последующих лет. Мы учимся понимать последствия, которые можно прогнозировать, составляя уравнение, средствами математического анализа, при этом наша формализация может быть проверена эмпирическими наблюдениями. Хотя многие из моделей, которые мы рассматриваем, могут на первый взгляд показаться грубыми упрощениями, их сила в простоте. Чем проще модель, тем яснее становятся предсказываемые её последствия исходя из самых базовых предположений.
Начнем с того, что сосредоточимся на моделировании того, как количество выпускников физико-математических классов растёт или сокращается с течением времени. Поскольку математические модели должны основываться на вопросах, вот несколько вопросов, которые следует учитывать: почему число выпускников иногда растёт, а иногда сокращается? Должны ли объемы выпусков вырасти до такой степени, что они станут неустойчиво большими, а затем сойдут до нуля? Если нет, то должно ли количество выпускников достичь некоторого равновесия? Если равновесие существует, какие факторы ответственны за него? Является ли такое равновесие настолько тонким, что любое нарушение может положить ему конец? Что определяет, следует ли данная тенденция одному из этих курсов или другому?
Начнём разбирать перечисленные вопросы с помощью самой простой математической модели изменяющейся численности населения.
1.1. Мальтузианская модель
Предположим, мы выращиваем не будущих математиков, а популяцию какого-то организма, скажем, мух, в лаборатории. Представляется разумным, что в любой данный день численность населения будет меняться из-за новых рождений, так что оно увеличивается за счет добавления определенной доли f от имеющегося населения. При этом часть d от имеющегося населения погибнет, условно, как бы цинично это не звучало, но многие профессиональные математики после выпуска вынуждены работать не по специальности, что смерти подобно.
Рассмотрим простейшую прикладную модель, которую предложил Томас Мальтус в своём очерке 1798 года о принципе народонаселения, неоднократно подвергавшемся всесторонней критике. Если люди живут в течение 70 лет, то мы ожидаем, что из большой популяции примерно 1/70 населения будет умирать каждый год; таким образом,
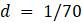
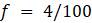
Вопросы для самопроверки:
– Объясните, почему для любой популяции
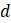
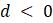
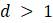
– Объясните, почему
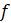
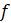
– Используя годы в качестве единицы времени, какие значения f и d будут уместны для моделирования числа выпускников естественно-научного профиля? Гуманитарного? Социально-экономического? Технологического и универсального?
Чтобы смоделировать значения P сфокусируемся на следующем за P изменении численности. Формально
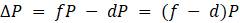
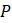
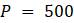
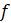
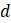
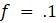
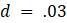
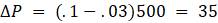
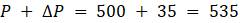
Введём несколько вспомогательных обозначений для упрощения восприятия математической модели. Пусть
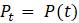
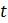
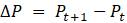
Ясно, что
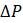
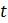
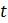
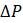
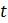
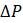
Теперь то, что нас в конечном итоге волнует, это понимание динамики популяции
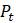
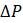
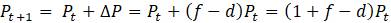
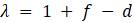

Популяризаторы науки часто называют константу
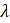
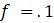
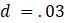
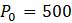
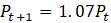
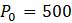
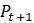
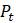
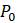
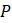
Таблица 1.1. Рост популяции по простой модели
Момент времени Численность
0 500
1 (1. 07)500 = 535
2 (1. 07)2500 = 572.45
3 (1. 07)3500 ≈ 612.52
… …
По закономерностям в таблице 1.1 легко перейти от рекуррентного соотношения для
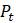
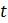
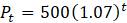
Может показаться странным называть
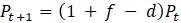
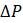
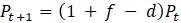
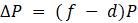
Пример. Предположим, что система математического образования имеет очень жесткие ограничения на целевые цифры приёма в ВУЗы (что вполне реалистично на просторах СНГ), по которым каждый год выпускается 200 молодых специалистов и все сотрудники пенсионного возраста уходят на заслуженный отдых. После того, как состоялся очередной выпуск, только 3% остаются работать по специальности, чтобы связать свою профессиональную деятельность с математикой, остальные либо эмигрируют, либо находят выше оплачиваемую работу. Чтобы написать разностное уравнение в этой системе, где будем измерять
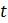
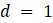
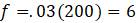
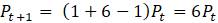
Вопросы для самопроверки:
– Будет ли общая численность математиков расти, а не уменьшаться при таких условиях?
– Предположим, вы не знаете эффективной «плодовитости», но знаете, что численность
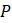
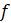
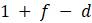
Обратите внимание, что в этой последней модели мы игнорировали тех математиков, кто не участвует в обучении математиков следующего поколения. Это на самом деле довольно распространенный подход и упрощает модель. Однако это означает, что делаются дополнительные предположения. Для конкретного направления точное количество учителей может мало влиять на то, как растет численность специалистов. Возможно, учителя всегда встречаются примерно в равном количестве с узкими специалистами, так что мы знаем, что общая численность людей, посвятивших жизнь математике, просто вдвое превышает число учителей математики. С другой стороны, численность профессиональных математиков может вести себя иначе, чем численность учителей математики, но независимо от того, мало ли учителей или их много, всегда достаточно, чтобы появление учителей происходило непрестанно. Таким образом, именно численность учителей математики является важным параметром для отслеживания, чтобы понять долгосрочный рост или сокращение числа профессиональных математиков в стране.



