Евразийское мышление. Вопросы науки и техники. Сборник 1

Из рисунка 4—3 видно, что

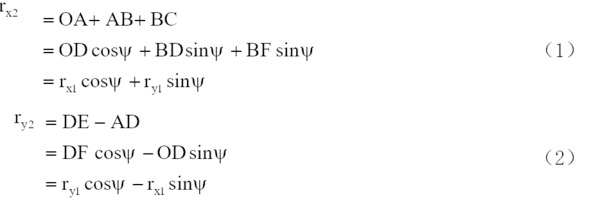
Видно, что соотношение координат в матричной форме, полученное вращением угла вокруг оси z, имеет вид:

2. Угол поворота объекта вокруг оси Y. Поскольку ось Y не перемещается, соотношение трансформаций x и z показано на рисунке 4—4.

Рисунок 4—4 Координатное соотношение вокруг осей Z, X и Y

Из рисунка 4—4 видно, что

3. Объект вращается вокруг оси X. Поскольку ось X не перемещается, соотношения преобразования Y и Z показаны на рисунке 4—5.

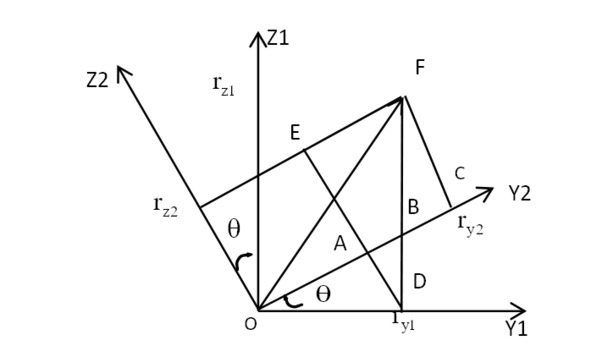
Рисунок 4—5 Координатное соотношение вокруг осей Z, X и Y

Из рисунка 4—5 видно, что

Угол ориентации объекта можно рассматривать как совокупность трех углов поворота, где угол поворота вокруг оси z записывается как угол курса, угол поворота вокруг оси y записывается как угол тангажа y, и угол поворота вокруг оси x называется углом крена 0.

После выпуска матрицы преобразования ориентации параметры матрицы формул (15) и (16) могут быть сопоставлены один к одному после последующего процесса фильтрации для определения трехосного угла ориентации. Конкретный процесс заключается в следующем.

Сопоставьте параметры уравнений (15) и (16) один за другим, возьмем три элемента в третьей строке уравнения (16), приравняем их g1, g2 и g3 соответственно и возьмем первый элемент уравнения ( 16). Первые два элемента столбца – это g5 и g4 соответственно.

Его значения следующие:

Затем я подставил кватернион в последний момент в формулу угла ориентации (19), чтобы найти эти три угла ориентации. Формула для окончательного получения угла ориентации выглядит следующим образом:

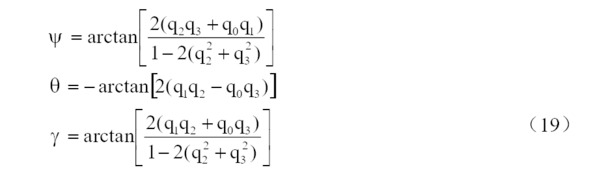
4.2. Решение параметров кватернионов.

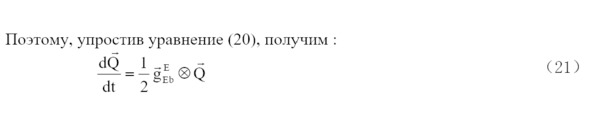
Затем преобразуйте его в матричную форму и получим уравнение (24).

4.3. Процесс фильтрации EKF. Расширенный фильтр Калмана (EKF) – это прикладное расширение фильтра Калмана, которое использует данные наблюдений системы для оптимальной оценки состояния нелинейной системы и фильтрации помех, таких как шум и дрейф. Этот алгоритм использует локальную линеаризацию для решения нелинейных задач путем вывода нелинейных уравнений.

Затем мы инициализируем фильтр и устанавливаем матрицу шума процесса Q, матрицу ошибок измерения R, матрицу состояний X и ковариационную матрицу P.

Поскольку параметры кватернионов в матрице преобразования отношения являются каноническими кватернионами и должны рассчитываться как нормализованные значения, полученные значения необходимо рассчитывать как нормализованные значения.

Берем значение акселерометра и нормализуем его.

Затем нормируем данные ускорения и магнитометра и вычисляем опорный магнитный вектор, векторная матрица которого обозначается как B.

Итак, возьмем частную производную матрицы H по матрице X. Среди них значения четырех вышеуказанных параметров могут быть получены по формуле решения теоретического ускорения (36) и формуле решения теоретического вектора магнитного поля (37), а значения акселерометра и магнитометра можно подставить в матрица переноса. Матрица H выражается так:

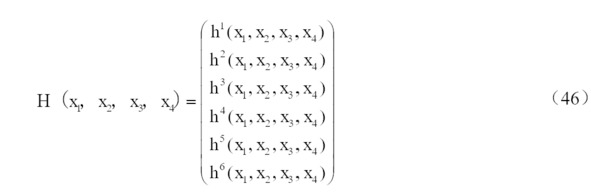
Среди них первые три функциональных выражения представляют собой теоретическое ускорение, а последние три функциональных выражения представляют собой теоретический магнитный вектор.

В процессе фильтрации на предыдущий момент k-1 происходит:

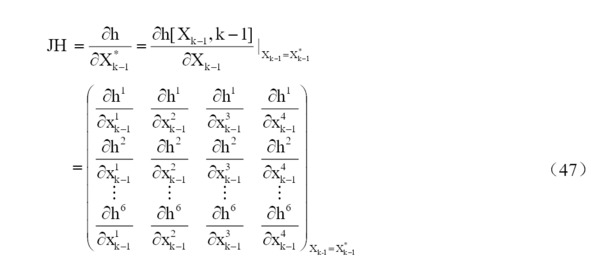
Тогда матрица Якоби матрицы H представлена в формуле (48).

Наконец, мы используем принцип рекурсии для непрерывной итеративной обработки формулы фильтрации, одновременно с этим обновляются данные и выводится значение матрицы состояния X:

Наконец, на основе предыдущей формулы расчета угла поворота (19) получается окончательный расчетный угол поворота.

Во всем этом процессе фильтрации кватернион эквивалентен промежуточному параметру, преобразующему нелинейное отношение в линейную форму для расчета. Путем постоянного обновления значения корректирующего гироскопа получается оценка кватерниона в следующий момент, а затем. Оценка кватерниона получается по формуле. Расчетный расчет кватерниона дает окончательный угол ориентации.

5. Программирование

5.1. Модуль программирования. Общий дизайн этого исследовательского проекта можно резюмировать в виде следующих трех пунктов: Во-первых, чтение данных MATLAB. Этот исследовательский проект представляет собой инерциальную навигационную систему, основанную на блоке инерциальных измерений 3DM-E10A, которая требует считывания данных инерциального блока через Matlab. Во-вторых, необходимо разработать функцию фильтра расчета ориентации и отфильтровать данные инерционного блока с помощью алгоритма фильтра. Третий – отображение формы сигнала в реальном времени, написание программы рисования в прерывании таймера для реализации процесса динамического рисования. Основная цель данного исследования – разработать программу MATLAB фильтрации ориентации для инерциальной навигационной системы на основе блока инерциальных измерений 3DM-E10A для отображения ориентации в реальном времени. Общий модуль программирования показан на рисунке 5—1.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «Литрес».

Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.