Уравнения движения в расширяющейся Вселенной

Для описываемой гипотезы ускоренное расширение Вселенной проблемой не является, однако замедленное является более удобным, поскольку предполагает более естественный процесс: исходная субстанция, исходный материал для вещества в некоторой области – в "возбуждённой" Материи – заканчивается. Гипотеза также приемлемо объясняет, почему пространство расширяется только вне гравитационно связанных областей: можно сказать, что повышенная напряжённость гравитационного поля препятствует переходу Материи в вещество, в элементы физического вакуума. Обилие вещества в них, видимо, препятствуют образованию новых «атомов пространства». Так сказать, трудно пробиться через толпу. Понятно, что эта гипотеза не нуждается в антигравитации тёмной энергии.

Также гипотезе не противоречит и сверхсветовое разбегание галактик. Они не движутся под действием сил, они не движутся по инерции – таких скоростей не допускает теория относительности. Увеличение, рост расстояний между ними за счет появления новых «атомов пространства» просто выглядит как их взаимное удаление, разбегание.

Тем не менее, инерционная трактовка расширения пространства после Большого Взрыва в литературе встречается:

"Гравитационные силы отталкивания в инфляционный период разгоняют частицы, а дальше они движутся по инерции. Так формируется хаббловский закон расширения" [3].

Но это, как мы уже отметили, неверно. Объекты во Вселенной не движутся (в смысле её расширения). Движутся, если можно так выразиться, интервалы между ними, расстояния, которые растут, вытягиваются. Эти "увеличивающиеся расстояния" наиболее правильно назвать расширяющимся пространством. Увеличивается именно пространство, растёт, расширяется, разбухает. Считается, что космологическое красное смещение является подтверждением расширения пространства, а не физического, механического движения галактик:

"… Какие факты указывают на то, что разбегание галактик не является движением собственно галактик, а именно движением вследствие расширения пространства …?"

"Собственно, космологическое красное смещение. … если волновой пакет распространяется в расширяющейся Вселенной, то расширение пространства обусловливает расширение волнового пакета, а значит, и изменение длины волны, соответствующей этому пакету" [4].

Точно так же, как завершился основной этап формирования вещественной реальности, точно так же должен рано или поздно завершиться и этап формирования дополнительных атомов пространства. Иначе говоря, скорость появления этих атомов должна снижаться. Следовательно, должна уменьшаться и скорость наблюдаемого расширения пространства, Вселенной. Это логически более естественный процесс, нежели ускоренное и даже постоянное до бесконечности расширение пространства.

Заметим, что механизм расширения пространства за счёт действия тёмной энергии выглядит несколько странно, как и само её называние. Утверждается, что плотность этой энергии неизменна, но тогда из каждой фиксированной области пространства вещество и тёмная материя со временем должны как бы "вытолкнуться". То есть, удельная плотность Вселенной должна стремиться к 75% от нынешней.

4. Логика расширения пространства

Давайте попробуем логически и аналитически разобраться, как вообще происходит расширение Вселенной с изложенной философской точки зрения. Для определенности механизм расширения представим, например, как монотонное удвоение атомов пространства, их умножение наподобие клеточного деления. Очевидно, что добавление новых "атомов пространства" выглядит как увеличение всех расстояний, причем реальное движение материальных объектов при этом не возникает.

Такой механизм позволяет объяснить также и причину расширение пространства между гравитационно связанными областями и его отсутствие внутри этих областей. Внутри гравитационно связанных областей, по всей видимости, "фоновой" области Материи труднее сформировать дополнительные атомы пространства. Здесь Материя, с одной стороны, исчерпала свой исходный материал, а, с другой стороны, сильное гравитационное поле просто противодействует появлению новых атомов.

Для большей наглядности проведем анализ формально с использованием аллегории железнодорожных путей со шпалами. Пусть расстояние между двумя объектами измеряется количеством шпал между ними. Примем, что исходное расстояние при t = 0 составляет одну шпалу r0 = 1.

Пусть удлинение, расширение пространства происходит монотонно таким образом, что его длина увеличивается за счет удвоения каждой шпалы в единицу времени. Здесь мы введем величину, которую назовём коэффициентом пространственного расширения (чтобы не путать его с масштабным фактором), равную в данном случае 2. Поэтому в следующий момент времени шпал будет уже две:

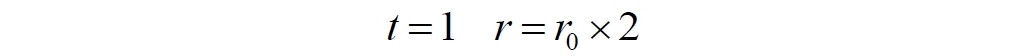
В следующий и дальнейшие моменты времени число шпал каждый раз удваивается:

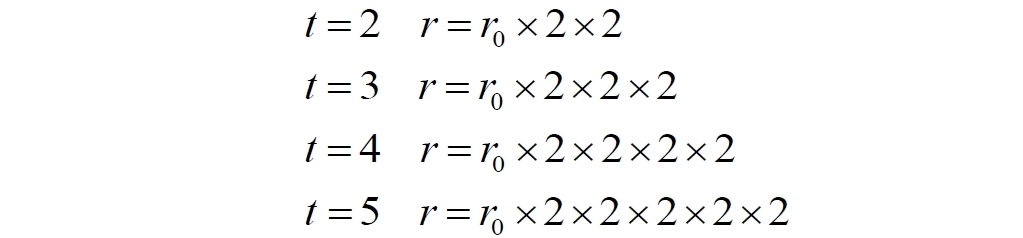
И так далее. Здесь уже можно обнаружить некоторое сходство с законом Хаббла, но для зависимости не скорости от расстояния, а расстояния от времени, поскольку очень хорошо видна закономерность:

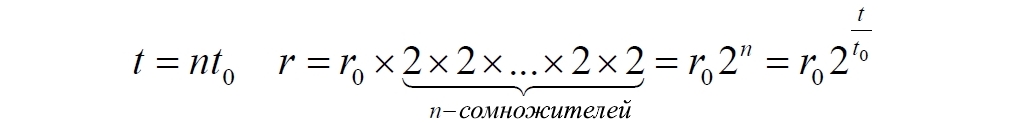
Однако мы использовали довольно радикальное значение параметра расширения пространства – удвоение.

Удвоение атомов пространства является, видимо, чрезмерно завышенной величиной. Поэтому выберем некоторую константу, значение которой пока не устанавливаем. Поскольку конечный результат, надо признаться, нам вообще-то известен, в качестве константы возьмем величину eH, которую также назовём коэффициентом пространственного расширения. Пусть в начальный момент времени расстояние между двумя объектами (галактиками) равно r0. Согласно выбранной модели за каждую единицу времени количество атомов пространства будет возрастать в eH раз. Поэтому в каждый следующий момент времени расстояние будет увеличиваться. Продолжив вниз левый столбец в следующей таблице, обнаруживаем закономерность (средний столбец), которую переписываем в короткое уравнение (справа):

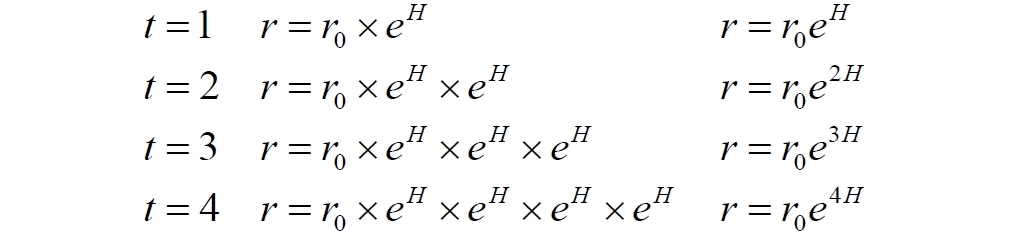
И так далее. Закономерность очевидна:

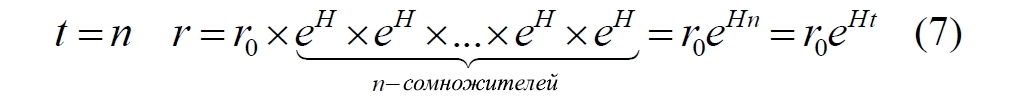
Или кратко:

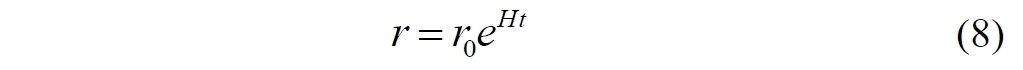
Уравнение описывает, как со временем увеличивается расстояние между двумя областями, находящимися в исходном состоянии на некотором расстоянии r0. Выше мы умышленно использовали константу в виде eH, чтобы получить именно такую запись (8), причем величина H окажется в точности равной постоянной Хаббла.

Легко заметить сходство уравнения (8) с законом Хаббла, но для зависимости не скорости от расстояния, а расстояния от времени. Если продифференцировать его по времени, то мы сразу же и получаем развёрнутый закон Хаббла:

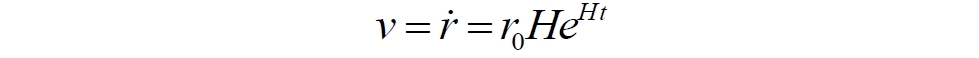
Замечаем, что последний сомножитель – это значение r, подставляем и получаем обычную запись закона Хаббла:

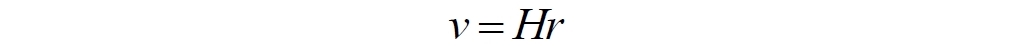
5. Интегральный закон Хаббла

Несложно показать, что при использовании изменяющегося во времени параметра eH(t) мы получим интегральное уравнение движения а(t) или r(t).

Для этого все одинаковые интервалы времени записываем количественно, а не в порядковом виде. Каждое следующее состояние пространства является расширением предыдущего интервала, уже испытавшего соответствующее расширение.

Отмечаем, что все интервалы времени Δti равны друг другу, а Hi – это значение параметра Хаббла, соответствующее текущему моменту времени этого i-го интервала. Для визуализации будем в уравнениях предыдущий интервал отделять от следующего закрывающей скобкой. Чтобы избежать "размножения" сопутствующих им открывающих скобок, мы их просто опустим, помня, что их может быть столько же, сколько и закрывающих:

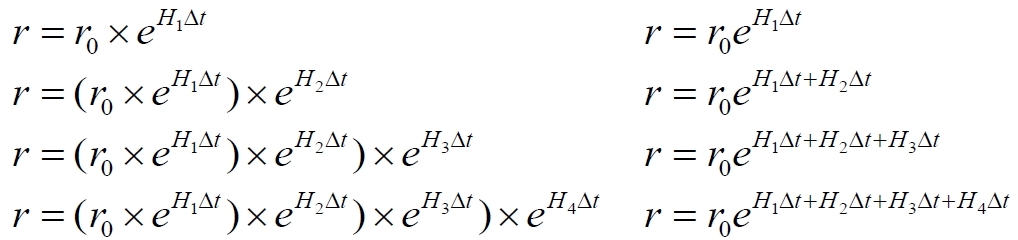
В первой строке показано, что расширение eHt испытал исходный интервал r0. Во второй строке расширение происходит теперь уже у этого уже расширившегося интервала в скобках. В третьей строке новым интервалом для расширения является итоговый интервал из второй строки. И так далее. Закономерность очевидна, она имеет вид:

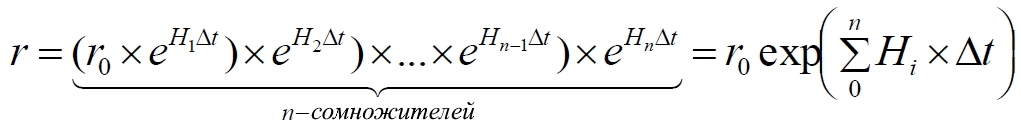
Обнаруживаем, что сумма произведений мгновенного значения параметра Хаббла, соответствующего каждому краткому интервалу времени, выглядит как интеграл. Если длины интервалов устремить к нулю, то получим интеграл:

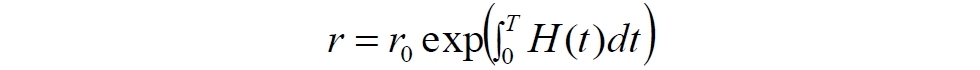
Верхним пределом интеграла является время T – сумма всех бесконечно малых интервалов времени dt просто потому, что количество слагаемых n как раз и равно количеству этих интервалов dt в общем времени: T = n×dt.

Выше такое же решение мы нашли для закона Хаббла с масштабным фактором (5) и (6). Уравнение описывает, как со временем увеличивается расстояние между двумя областями, находящимися в исходном состоянии на некотором расстоянии r0. Выше мы умышленно использовали константу в виде eH, чтобы получить именно такую запись (8), причем величина H окажется в точности равной постоянной Хаббла.

В заключение покажем, как с помощью этих уравнений производится построение диаграмм движения на примере условной галактики, сверхновой, находившейся в начале расширения пространства на удалении от Земли в 3 млрд. световых лет. Для наглядности рассмотрим условную Вселенную, расширяющуюся с параметром Хаббла H(t), имеющим множество изломов: участков убывания и возрастания.

На рис.1 этот переменный параметр Хаббла представлен графиком 105xH(t), где масштабный множитель 105 использован, чтобы график был хорошо различим, а его некруглое значение – чтобы он имел меньше пересечений с другими графиками. Интервал времени диаграмм равен 14 млрд. лет.

Используя уравнение (7), производим построение графика дистанций R(t). Построение производим по табличным данным, в которых текущее удаление рассчитывается как предыдущее, испытавшее шаговое расширение, расширение с текущим значением параметра Хаббла за единичный интервал времени.

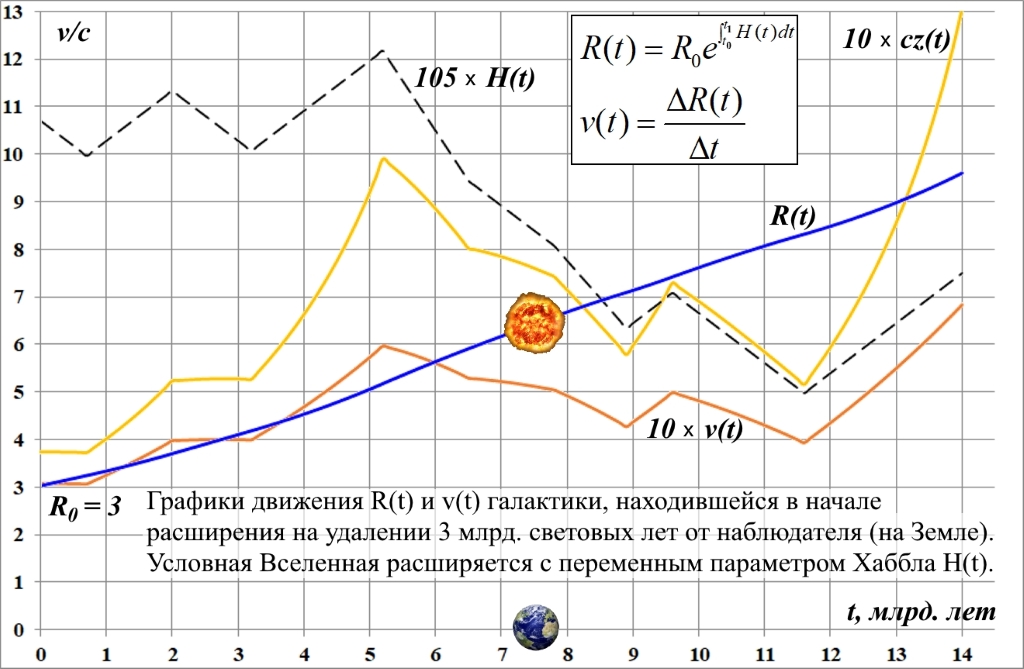
Рис.1. Пример диаграмм движения для переменного H(t)

График скорости v(t) строим c 10-кратным масштабом простым вычислением прироста дистанции за интервал времени этого прироста. Шаг времени step выбран равным 0,1 млрд. лет. Для сравнения приведён также график скорости с 10-кратным масштабом, определяемой для больших значений красного смещения точным обратным уравнением, переводящим скорость в красное смещение:

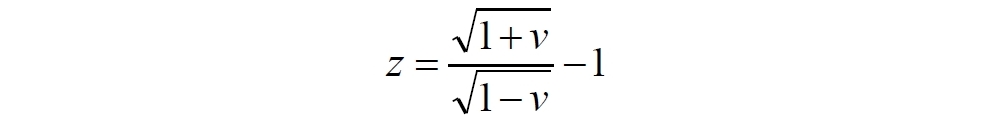
Как видим, расхождение скоростей на рисунке существенное. Скорость, определяемая простым умножением красного смещения на скорость света получается почти в 2 раза больше реальной скорости объекта. Известно, что приблизительное равенство cz ≈ v выполняется только при малых значениях красного смещения, z < 0,1.

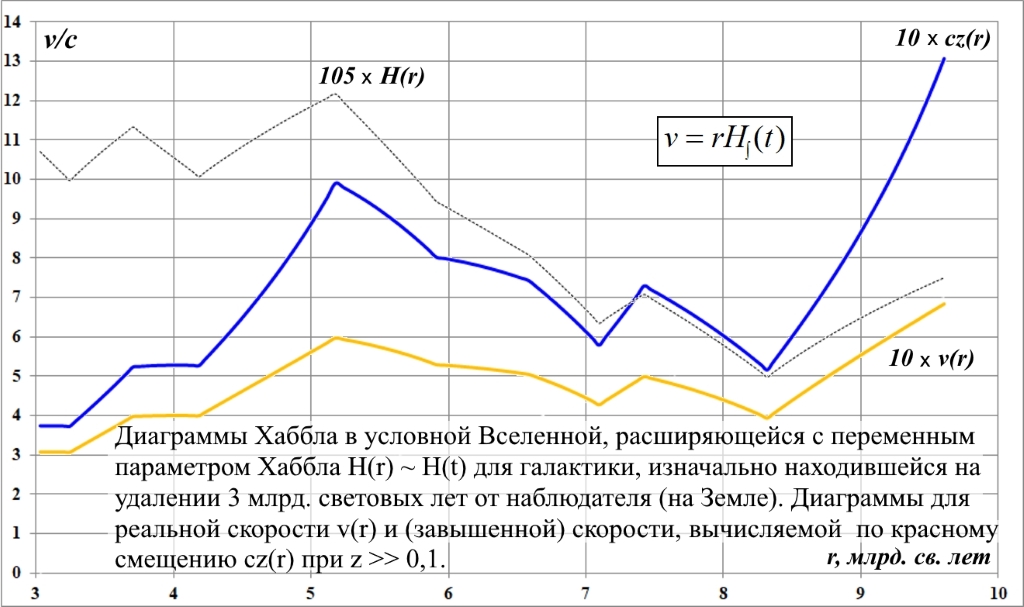
Рис.2. Диаграммы Хаббла для v(r) и cz(r) во Вселенной с параметром Хаббла H(r)

На рис.2 приведены традиционные диаграммы Хаббла для этого условного параметра Хаббла H(t). В вычислениях использовано интегральное значение параметра Хаббла (5).

Литература

1. Боджовальд М., В погоне за скачущей Вселенной, журнал "В мире науки", Космология, 2001, № 1, URL: http://www.chronos.msu.ru/old/RREPORTS/bodzhovald_pogonya.html

2. Инфляционная стадия расширения Вселенной, Элементы, URL: http://elementy.ru/trefil/21082

3. Космология ранней Вселенной, Соросовская Энциклопедия, 2005, URL:

http://www.astronet.ru/db/msg/1210276

4. Расширение пространства со сверхсветовой скоростью?, URL: https://otvet.mail.ru/question/62024653

5. Смолин Л., Атомы пространства и времени //ВМН, № 4, 2004

6. Теория стационарной Вселенной, Элементы, URL:

http://elementy.ru/trefil/21183?context=25284