Диаграммы Пенроуза – что это такое?

Пометим на рис.5a точками abcde несколько смежных диагоналей квадратов координатной сетки. Под квадратом понимается прямоугольник со сторонами x = y = 1, хотя действительно квадратами выглядят только диагональные.

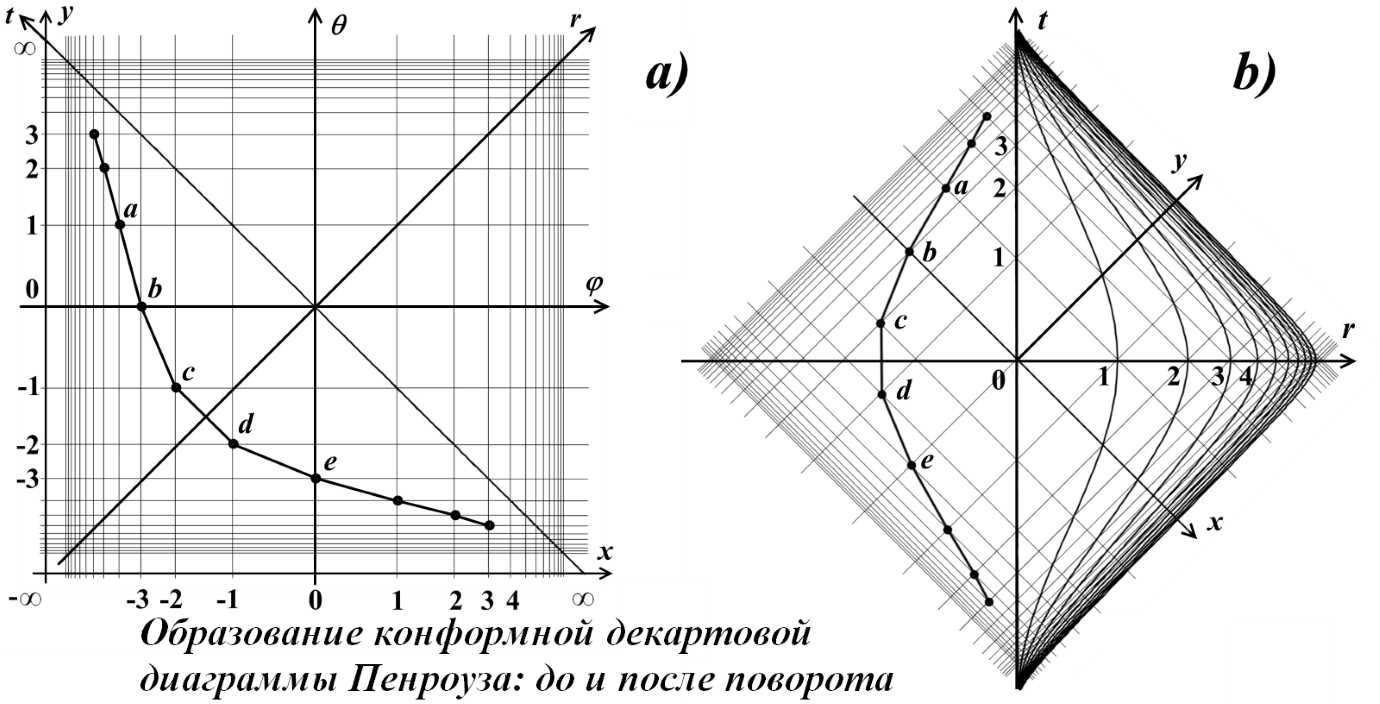
Рис.5. Конформная декартова диаграмма Пенроуза до и после поворота

Тем не менее, аналитически в системе координат x-y рисунка рис.5a любая из таких дуг описывается уравнением y = ±x + C, то есть, является линией с наклоном в 45о к осям этих координат. Это можно отчетливо увидеть по значениям координат точек abcde. Метрически вдоль осей φ и θ откладываются значения углов, но обозначаются эти точки соответствующими величинами арктангенсов.

Такие же последовательности координат (x, y) можно составить и для всех других возможных точек, в нашем случае с целочисленными координатами, для любой подобной же кривой-дуги на диаграмме. Обратив внимание на явную закономерность, запишем уравнения этих линий в более компактном общем виде:

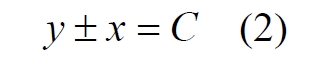
Смысл этого уравнения кажется достаточно очевидным: это обобщённое уравнение всех возможных кривых линий на рис.5a в системе конформных сжатых осей x и y. Значения φ и θ откладываются вдоль тех же осей x и y (оси коллинеарны), но по их собственной шкале от ‑π/2 до +π/2, в чем, собственно, и состоит конформное сжатие, то есть, диаграмма Пенроуза – это квадрат со сторонами, равными π.

Из уравнения (2) следует, что каждая дуговая линия имеет некий номер C и соответствующее ему уравнение при любых значениях x и y на всей числовой оси. Иначе говоря, константа C является обобщённым обозначение номеров кривых линий. Теперь вспомним, что все эти кривые линии мы построили, соединяя диагонали смежных четырёхугольников. Можно назвать эти линии удлинёнными диагоналями. Но на этом же рисунке видно, что и прямые линии исходной, тангенциальной сетки являются в свою очередь точно такими же удлинёнными диагоналями, если координатной сеткой считать кривые линии, дуги. То есть, наборы прямых и кривых линий являются по отношению друг к другу координатными сетками. Иначе говоря, имея указанную сетку из кривых линий, мы таким же образом можем построить и прямые линии, просто соединяя диагонали смежных криволинейных четырёхугольников.

Если теперь уже дуги рассматривать как координатную сетку, то обнаружится, что номера дуг остались теми же самыми. То есть, дуга, проходящая через координату xy(3,0) и имеющая, соответственно, номер C = 3, точно также проходит через такую же координату rt(3,0) и имеет точно такой же номер C = 3. Вот здесь мы и обнаруживаем конформную взаимосвязь между координатами x-y и координатами r-t, описываемую уравнениями арктангенсов.

В декартовой системе координат на рисунке рис.5 массивы прямых ортогональных линий и криволинейных условно ортогональных линий образуют каждая своеобразную координатную сетку. То есть, на рис.5a в качестве координатной сетки мы использовали прямые линии и построили в этих координатах массивы криволинейных линий. Но и, наоборот, эти кривые линии мы можем рассматривать также как линии координат, сетку. На рисунке рис.5a оси координат r-t и их дуга abcde имеют наклон в 45 градусов.

Хорошо видно, что эта диаграмма Декарта на рис.5a оказалась похожей на квадрат диаграммы Пенроуза рис.2, только без поворота (и с единственной дугой). Если теперь эту диаграмму Декарта повернуть на 45 градусов и добавить остальные дуги, мы получим классическую диаграмму Пенроуза. При этом окажется, что бывшие прямые координатные линии превратились в изотропные нулевые геодезические, линии света, а декартовы линии света – в координатные линии диаграммы Пенроуза рис.5b. Линейные размеры, координаты новой оси r изменяются в некоторых ограниченных пределах (точнее, от –π/√2 до +π/√2), в то же время как каждой из них присваивается значение C:

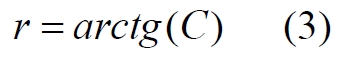
Обратив внимание на то, что знак в выражении (2) соответствует ортогональным дугам, раскрыв его и подставив в выражение (3), мы получаем два уравнения конформного преобразования между координатами r-t и x-y:

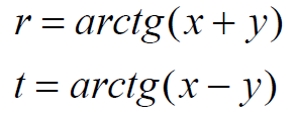
Особо отметим обнаруженную интересную особенность рассмотренного метода конформных преобразований координат: поворот сетки позволяет поменять ролями сетку и нулевые геодезические. Нанесение желаемых светоподобных геодезических позволяет по ним построить, получить затем соответствующую координатную сетку. Если теперь нанести на полученную диаграмму все обозначения, соответствующие традиционной ромбовидной диаграмме Пенроуза с бесконечными границами и все дуги, мы получим диаграмму рис.2.

Здесь мы наглядно видим сущность конформного преобразования на диаграммах Пенроуза. На рис.5a вертикальные и горизонтальные прямые линии образуют нелинейную координатную сетку. Мы принимаем скорость света равной единице c = 1. Производная уравнения движения какого-либо объекта – это его скорость. Для света можно записать

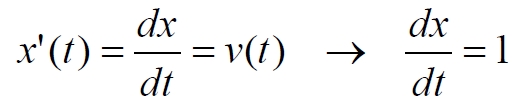
Здесь производная – это тангенс угла наклона графика к вертикальной оси на диаграмме, к оси времени. Условно говоря, график движения света проходит диагонально через "квадратики" координатной сетки. Это демонстрирует линия abcde на рис.5a. Понятно, что при нелинейной градации координатной сетки "квадратики" условны, визуально все они являются прямоугольниками. Тем не менее, график света всё равно проходит диагонально через эти прямоугольники. То есть, линия abcde является линией света. В таком виде она, во-первых, не выглядит конформной, наклонённой под 45 градусов, а, во-вторых, сильно искривлена. Однако между этой линией и координатной сеткой есть однозначная связь: в каждом "квадратике" конформность и прямолинейность линии просматривается отчётливо.

Для нас, в сущности, не имеет значение, как выглядит координатная сетка, для нас важно, чтобы линии света были конформными, изотропными. И здесь следует отметить гениальную догадку Картера-Пенроуза. Они заметили, что координатная сетка выглядит как изотропные линии света, если за оси координат взять диагональные линии. Для этого нужно просто повернуть квадрат на 45 градусов – рис.5b. Теперь бывшие ранее координатной сеткой линии все стали выглядеть как изотропные линии света. Все они наклонены под 45 градусов и строго прямолинейны.

Бывшие ранее линиями света криволинейные линии, в частности, линия abcde сохранили строго однозначную связь с теперь уже прямолинейными линиями, которые теперь можно считать линиями света. То есть, эту криволинейную сетку мы можем, соответственно, рассматривать как координатную. Поставленный на диагональ квадрат теперь отвечает главному требованию: диагональные линии на нём стали изотропными линиями света. Они прямолинейны и имеют угол наклона в 45 градусов.

2

M

-диаграмма Пенроуза

Из полученной диаграммы мы так же можем сформировать и так называемое максимально расширенное решение Шварцшильда для вечной Чёрной дыры – рис.14 и рис.6f, содержащее сингулярности и параллельную Вселенную. Для этого необходимо заменить обозначения r = ‑∞ на r = 2m. Понятно, что на оси i0i0 значения r = const также следует заменить на соответствующие. Диаграммы с левым значением 2m назовём 2M-диаграммами Пенроуза.

На диаграммах этого вида сразу же обнаруживается противоречие: на такой диаграмме невозможно корректно произвести разметку координатных линий времени. Иначе говоря, на диаграммах с левым горизонтом событий r = 2m равномерная шкала времени t = const становится невозможна. В первую очередь это связано с тем, что разметка линий r = const потребовала специфического подхода: шаг, расстояние между двумя линиями r = const на всём протяжении диаграммы неизменным сделать невозможно.

Действительно, чтобы обеспечить традиционный вид координатной сетки, мы должны слева и справа диаграммы нанести одинаковое количество дуг r = const. Но слева диапазон расстояний конечен и равен некоторому количеству координатных дуг, а справа – он бесконечен. Какое бы определённое значение для центральной оси r0 = const мы ни выбрали, кроме r0 = ∞, интервал слева также будет конечным. Но главная проблема не в этом. Поскольку левая часть диаграммы – это горизонт событий Чёрной дыры r = 2m, дискретность координатной сетки должна экспоненциально уменьшаться. Чем ближе к горизонту, тем мельче деления шкалы, интервалы между линиями. Это исключает любую возможность установить их конечное количество, которое стремится к бесконечности. Справа от центра диаграммы число координатных линий также стремится к бесконечности, но дискретность этой сетки может быть как постоянной, так и экспоненциально изменяющейся – возрастающей или убывающей. В любом случае пределом этой шкалы должна быть бесконечность.

Можно воспользоваться следующим очевидным способом преобразования на квадратной диаграмме левого бесконечного горизонта в конечный. Это простое вытягивание, смещение линии координатной сетки r = 2m до положения левого горизонта событий. Остальные линии сетки левее этой просто "выталкиваются" за пределы диаграммы рис.6. Однако анализ показал безуспешность этого способа.

Как показано на рисунке стрелкой, координатная времениподобная линия r = 2m скачкообразно, пошагово перемещается сначала в нулевую позицию в центре диаграммы, затем в точки ‑1m (рис.6b), ‑2m (рис.6с), ‑4m (рис.6d), ‑7m (рис.6e), ‑10m (рис.6f). При этом в центре диаграммы поочерёдно оказываются координатные линии, соответственно, r = 3m, r = 4m, r = 6m, r = 9m, r = 12m. Разметка сетки при этом сохраняет свой исходный изотропный и конформный вид. Все нулевые геодезические и световые конусы, как ожидается, также сохраняют свои свойства.

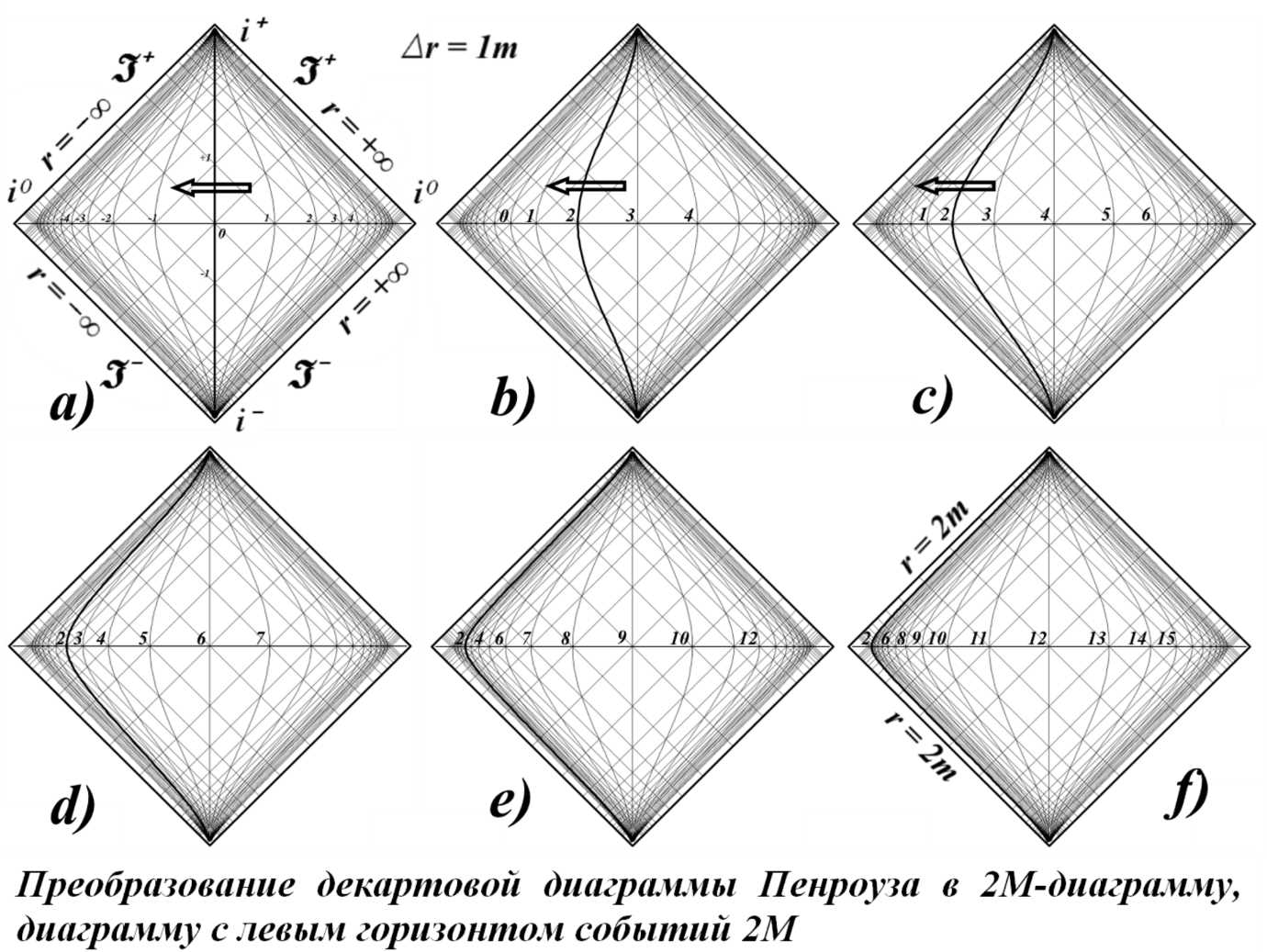
Рис.6. Преобразование диаграммы в 2M-диаграмму

Очевидно, что после завершающего перехода координатной линии r = 2m на позицию левого горизонта событий, в центре диаграммы окажется координатная линия со значением +∞. Также очевидно, что никакие геодезические на конечном удалении от горизонта событий в этом случае изобразить на такой диаграмме будет уже невозможно: все они сожмутся в бесконечно тонкую линию вблизи левого горизонта событий. С другой стороны, сдвигаемая влево времениподобная координатная линия r = 2m никогда не превратится в светоподобную линию горизонта событий, в пределе оставаясь от неё на планковском удалении. В этом случае очевидно, что любое изображённое на диаграмме событие или движение не будет иметь никакого отношения к горизонту событий Чёрной дыры. Движение даже к его отдалённой окрестности, например, до r = 1000m будет длиться вечно, только внешне напоминая падение на горизонт r = 2m. Визуально, ввиду мелкой детализации, будет казаться, что эта линия является корректным горизонтом событий (рис.6f), но при увеличении масштаба (как под микроскопом) фактически не будет никакого различия для значений этих промежуточных "горизонтов". В равной степени мы можем поставить возле них вместо r = 2m как r = 2000m, так и r = –∞, характер диаграммы будет в точности таким же. В целом эта диаграмма становится тождественной обычной диаграмме с двумя пространственноподобными бесконечностями i0.

Ещё одной серьёзной проблемой является то, что из-за различной дискретности сетки слева и справа диаграммы, использовать постоянные значения интервалов на всей шкале невозможно. Конечность интервала слева исключает такую возможность. То есть, мы в принципе можем установить шаг делений справа Δr = 1 = const, либо иной другой постоянный шаг. Но на левой стороне диаграммы никакой постоянный шаг невозможен. Получается, что сетка диаграммы должна быть размечена двумя разными шкалами, что, очевидно, весьма неудобно.

Однако есть вариант компромиссной шкалы, единой на всём диапазоне расстояний. Это шкала r, размеченная степенным рядом. Каждому делению шкалы присваивается значение 2+2n, где n – номер линии r имеет значения от ‑∞ до +∞. На такой диаграмме для наглядности центру может быть приведена в соответствие, например, координата r = 4m, соответствующая номеру n = 1.

В литературе на такие 2M-диаграммы координатная сетка наносится крайне редко, а если и наносится, то условно, без каких-либо обозначений, шкал. При этом светоподобные геодезические и световые конусы используются широко. Поэтому попытка аналитически построить соответствующую координатную сетку вполне оправданна. Выбор уравнения степенного ряда для сетки r = const позволил вполне приемлемо такую сетку построить.

Однако компромиссная шкала имеет собственную проблему. На диаграммах с такой шкалой оказалось невозможным корректно изобразить световые конусы, поскольку на них светоподобные геодезические оказались кривыми линиями. Проблема вызвана тем, что на такой диаграмме невозможна равномерная шкала времени – возникает так называемая анизотропия времени.

Алгоритм построения диаграммы Пенроуза

Исходя из возможных видов координатных параметров в трёхмерном пространстве, можно выделить четыре различные системы координат. Параметрами, задающими однозначное положение объекта в трёхмерном пространстве должно быть три. При использовании в качестве таких параметров линейных отрезков – ρ или углов – φ, можно сформировать четыре группы, четыре набора координатных параметров:

3ρ+0φ (три линейных параметра и ни одного углового). Это обычная декартова система ортогональных координат;

1ρ+2φ – это классическая полярная система координат;

0ρ+3φ – это широко применяемая в астрономии, космологии система координат, которая в такой формулировке явно, детально нигде не описана;

2ρ+1φ – система координат, об использовании которой ничего не известно.

Декартова и полярная системы координат широко известны, и в пояснениях, видимо, не нуждаются. Третья система, космологическая использует, в частности, три опорные, реперные точки, образующие треугольник с известными сторонами. Из этих точек определяются три координатных угла до исследуемого объекта в космосе, в результате чего образуется треугольная пирамида, в которой можно вычислить длины её граней. Может возникнуть ощущение, что на самом деле используется 6 параметров. Но стороны реперного треугольника на самом деле не влияют на величину удалённости объекта в космосе и на расстояния между ними.

Декартова, ортогональная система координат имеет разновидности по используемой градации, разметке осей. Чаще всего это линейные, равномерные градации. Также часто используются оси с логарифмической градацией. Эти системы позволяют отобразить объекты и процессы конечной протяжённости. Рассматриваемые диаграммы Пенроуза являются вариантом декартовой системы координат в обычном смысле этого понятия, шкалы осей которой "скомпрессированы", то есть, сжаты по определенному алгоритму. По аналогии с понятием "логарифмическая" шкала, такой алгоритм можно назвать алгоритмом "тангенсического" сжатия. Понятно, что в данном случае для сжатия шкалы вместо функции логарифм используется функция тангенс, вернее, его обратная функция – арктангенс.

Процесс такого сжатия шкал или процесс конформного преобразования представляет собой, по сути, построения новой шкалы для координат расстояния r и времени t как функции от этих переменных в некоторой исходной системе координат u-v (1).

Иначе говоря, мы строим в системе координат u-v семейство линий, которые образуют новую координатную сетку. При этом из уравнений видно, что новая сетка оказывается заключенной в квадрат со стороной π, поскольку при изменении величин r и t в диапазоне от минус до плюс бесконечности, функции u и v изменяются в диапазоне от минус π/2 до плюс π/2.

Для нанесения координатной сетки сначала для каждого значения t = ‑n, …, ‑2, ‑1, 0, 1, 2, …, n строится сплошная линия r = ‑m…m. При этом на диаграмму наносятся дуговые линии, вытянутые от i- к i+. Затем для каждого значения r = ‑m, …, ‑2, ‑1, 0, 1, 2, …, m строится сплошная линия t = ‑n…n. При этом на диаграмму наносятся дуговые линии, вытянутые между точками i0.

При таком построении сетка одной из осей будет иметь вид рис.7a. Как видно на рисунке, сетка получилась с наклоном. Для наглядности на сетке показаны действительные оси координат u-v, в которых она построена, и конформные оси t-r, которые и предполагается использовать в дальнейшем. Для приведения масштабной сетки к обычному виду, когда её нулевая ось расположена либо вертикально, либо горизонтально, полученную сетку нужно просто повернуть на 45 градусов против часовой стрелки. В этом случае мы получим сетку оси времени t, как показано на рис.7b. После этого мы можем нарисовать по указанным уравнениям конформного преобразования вторую масштабную сетку и повернуть её теперь на 45 градусов по часовой стрелке. В результате мы получим сетку оси r, как показано на рис.7с. Объединив эти обе сетки, мы получим полную сетку диаграммы, как показано на рис.7d. Теперь мы можем нанести на рисунок все необходимые обозначения, в результате чего будет получена полная "пустая" диаграмма Пенроуза, как показано на рис.7e. Слово "пустая" означает, что на диаграмме нет никаких событий, мировых линий.

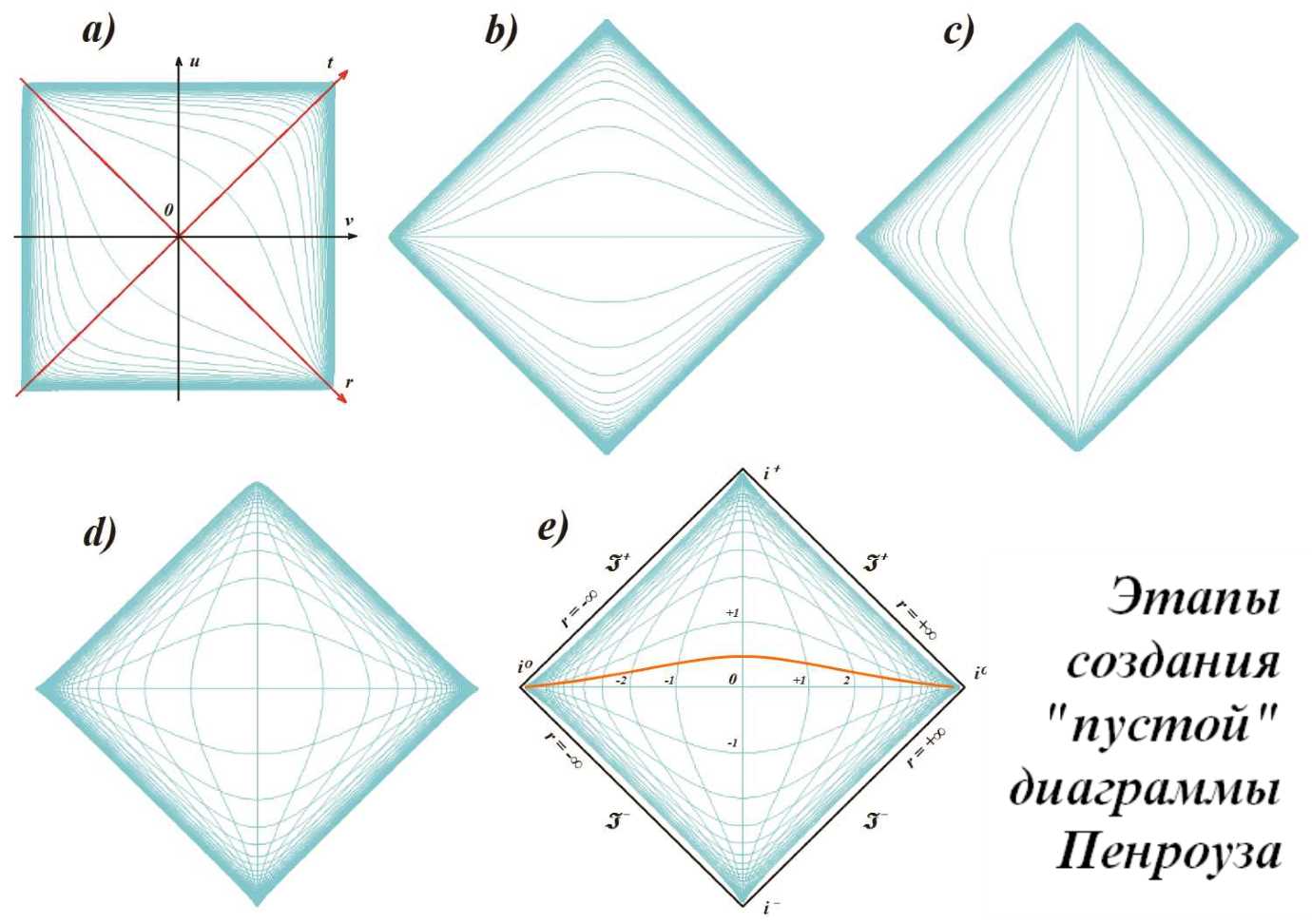
Рис.7. Последовательность создания "пустой" диаграммы Пенроуза

Собственно алгоритм построения сеток достаточно прост. Для удобства поворот сеток производится сразу же, в момент их построения. Поскольку алгоритм прост, приведем его в неформальном виде, в виде словесного описания:

Цикл 1: Для каждого –М < t < +M c шагом T

Цикл 2: Для каждого –М < r < +M c шагом R

Вычислить u = arctg(t + r) и v = arctg(t – r)

Повернуть полученную точку a(u, v) на 45 градусов по или против часовой стрелки (зависит от назначения линий сетки – время или расстояния)

Вывести полученную точку а(u, v) на координатную плоскость

Конец Цикла 2

Конец Цикла 1

Буквой М названа условная бесконечность, то есть, число большое, но не превышающее возможностей вычислительной системы (компьютера). Шаг T подбирается из соображений частоты линий на диаграмме. Слишком много линий просто затемнят картину. Из этих же соображений цвет линий сетки выбран ярко-бирюзовым. На его фоне линии другого цвета (мировые линии) просматриваются вполне отчетливо.

Теперь на диаграмму можно вывести любые события и мировые линии. Для этого используется точно такой же алгоритм, но только его "внутренняя часть", без циклов. По требуемой функциональной зависимости мы выводим последовательность точек a(u, v) (с поворотом!) и при необходимости соединяем их отрезками линий. Частота вывода линий – это темп реального хода времени, если мы создаем анимацию. Интервалы, очевидно, должны быть достаточно малыми, чтобы была незаметна ломаная структура линий. На рис.7 дискретность каждой дуговой линий составляет R=800, поэтому они выглядят как гладкие кривые. Для наглядности на анимации добавлена ещё одна линия – линия настоящего t = tнаст. У нас она обычно окрашена в оранжевый (горчичный) цвет. Мировые линии событий могут иметь произвольные цвета. Мировые линии света и тахионов имеют предпочтительные цвета – красный, малиновый.

Динамические диаграммы Пенроуза

Теперь, имея уравнения преобразования координат, мы можем изобразить на диаграмме Пенроуза любую мировую линию. Для этого нам нужно знать только уравнение её движения r(t). Более того, мы можем нарисовать последовательность диаграмм для каждого момента времени по этим уравнениям и соединить их в анимацию, динамическую последовательность кадров. Пример кадра такой анимации для четырех разных мировых линий изображен на рисунке:

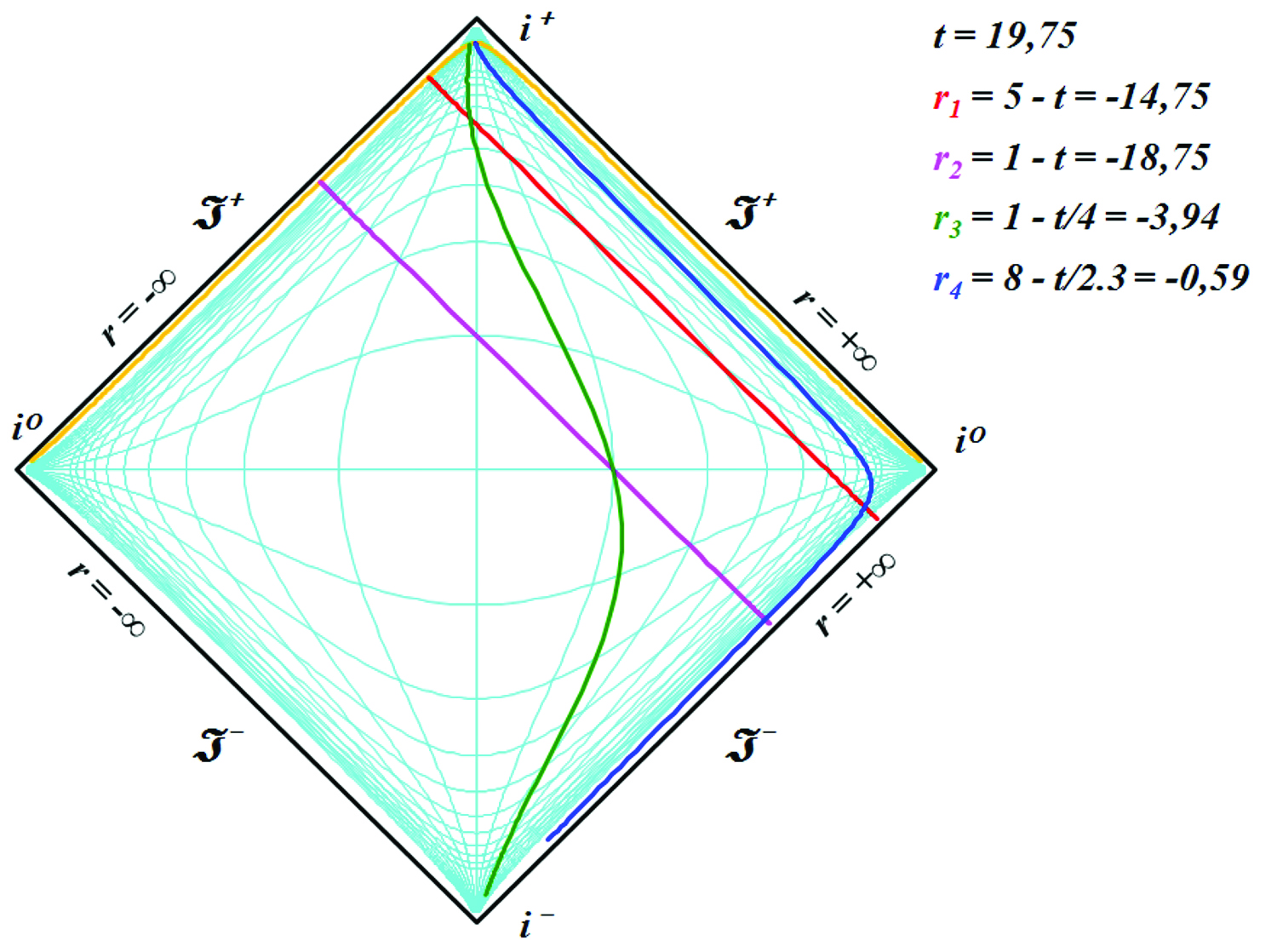
Рис.8. Мировые линии на динамической диаграмме. Анимация: http://samlib.ru/img/p/putenihin_p_w/diapen242/fig08.gif

На кадре из динамической диаграммы изображены четыре произвольные мировые линии, имеющие начало в момент времени t = ‑20, где размерность времени может быть произвольной, как указано выше. Две из линий – светоподобные и соответствуют лучам света, испущенным в точках r = 1 и r = 5, причем размерность расстояния соответствует размерности времени. Другими словами, если расстояние измеряется в световых годах, то время – в годах; если время в минутах, то расстояние – в световых минутах и тому подобное. Для каждой мировой линии на рисунке приведены их уравнения, а на диаграмме цвет линии соответствует цвету названия функции.

Понятно, что в динамике мировые линии могут начинаться в любой точке диаграммы ниже линии настоящего, а заканчиваться должны на ней. Никаких событий выше линии настоящего не может быть, только ожидаемые, предполагаемые, которые могут произойти в будущем.

Как видно на динамической диаграмме, мировые линии пересекаются. Это означает, что испущенные световые лучи или времениподобные объекты (тела) встречаются в одной точке одномерного пространства-времени, двигаясь вдоль одной линии. Столкновение тел или поглощение лучей определяется тем, в каком направлении они движутся, что можно явно вычислить по уравнениям их мировых линий.

В качестве примера попробуем задать уравнение мировой линии такое, чтобы она проходила вблизи центра диаграммы. Как и в полярных координатах, на этой диаграмме изображено всё существующее пространство-время: и видимая Вселенная, и вся Вселенная за видимым горизонтом, от Большого Взрыва и до конца нашей реальности, ничто не может быть изображено вне диаграммы.

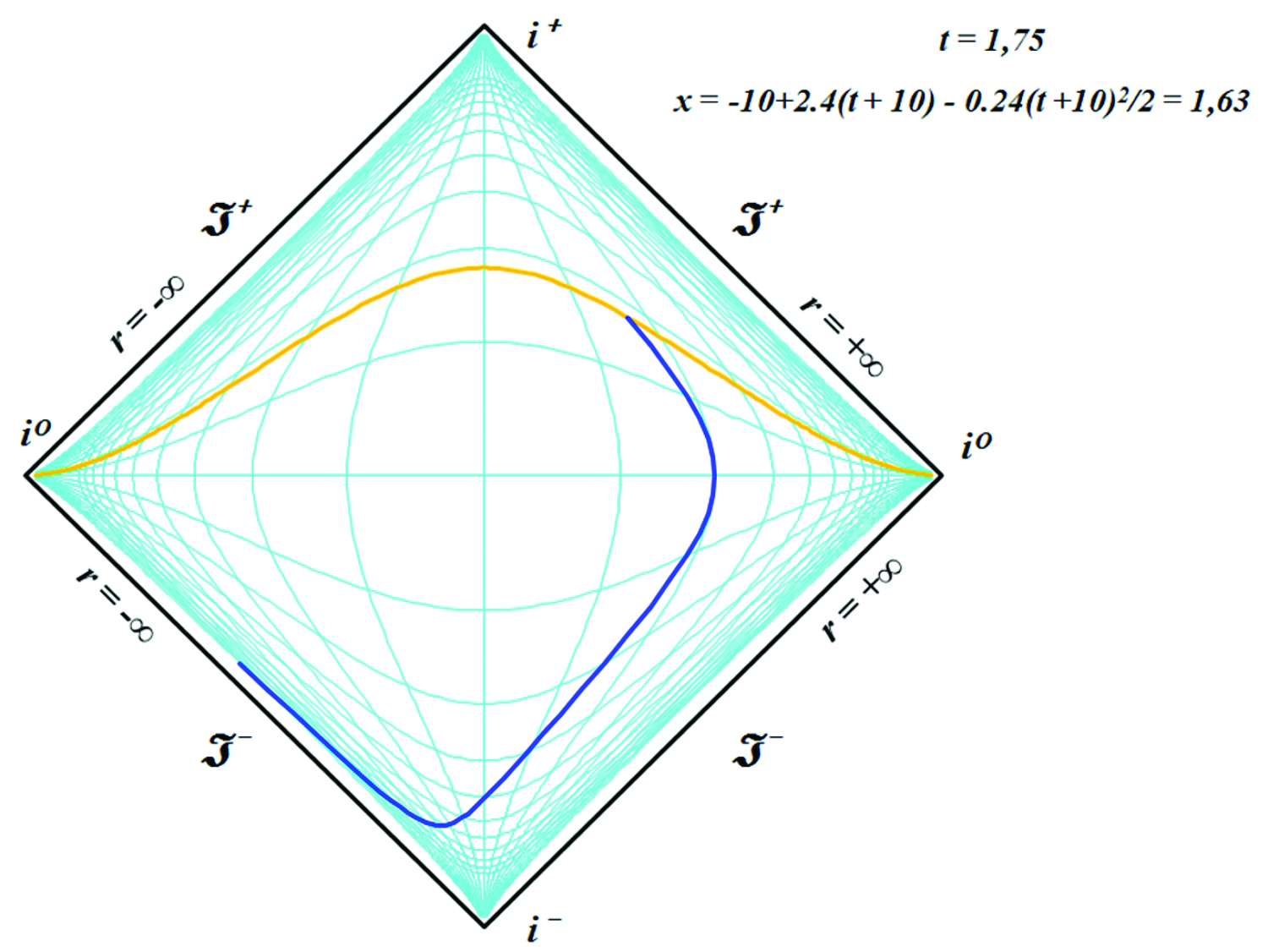
Рис.9. Пример мировой линии на динамической диаграмме Пенроуза по уравнению, рассчитанному из заданных условий. Анимация: http://samlib.ru/img/p/putenihin_p_w/diapen242/fig09.gif

Синим цветом изображена мировая линия события по выведенному уравнению, которое приведено в правом верхнем углу диаграммы. Значение уравнения на рисунке вычислено для момента времени t = 1,75. Можно заметить, что на нижнем отрезке траектории тело движется по пространственноподобной траектории, то есть, со сверхсветовой скоростью, как тахион. Проверку на корректность уравнения движения для построения диаграммы должен производить его автор, отслеживая скорость тела. Разумеется, "отсекать" недопустимые значения траекторий может и алгоритм автоматизированного, компьютерного построения диаграмм.

Динамическая диаграмма обмена световыми сигналами

Как правило, чаще всего диаграммы Пенроуза используются в общей теории относительности при рассмотрении неинерциального (с ускорением) движения или движения с учетом гравитационных сил, например, действия космологических Черных дыр. Однако нет никаких препятствий для использования их и для исследования инерциальных систем отсчета – ИСО.

В этом случае следует формировать столько диаграмм, сколько на ней имеется инерциальных участников движения. Рассмотрим случай обмена световыми сигналами теперь уже для двух таких ИСО – А и В. Диаграммы в виде анимаций представлены на рис.10.

На рисунке представлены диаграммы, полностью соответствующие диаграммам Минковского. Слева – ситуация с точки зрения неподвижного наблюдателя ИСО В, справа – ИСО А.

В некоторый момент времени из ИСО B испускается световой сигнал r3, который достигает ИСО A. В этот же момент времени оттуда отправляется ответный световой сигнал r4. Через какое-то время этот сигнал достигает ИСО В.

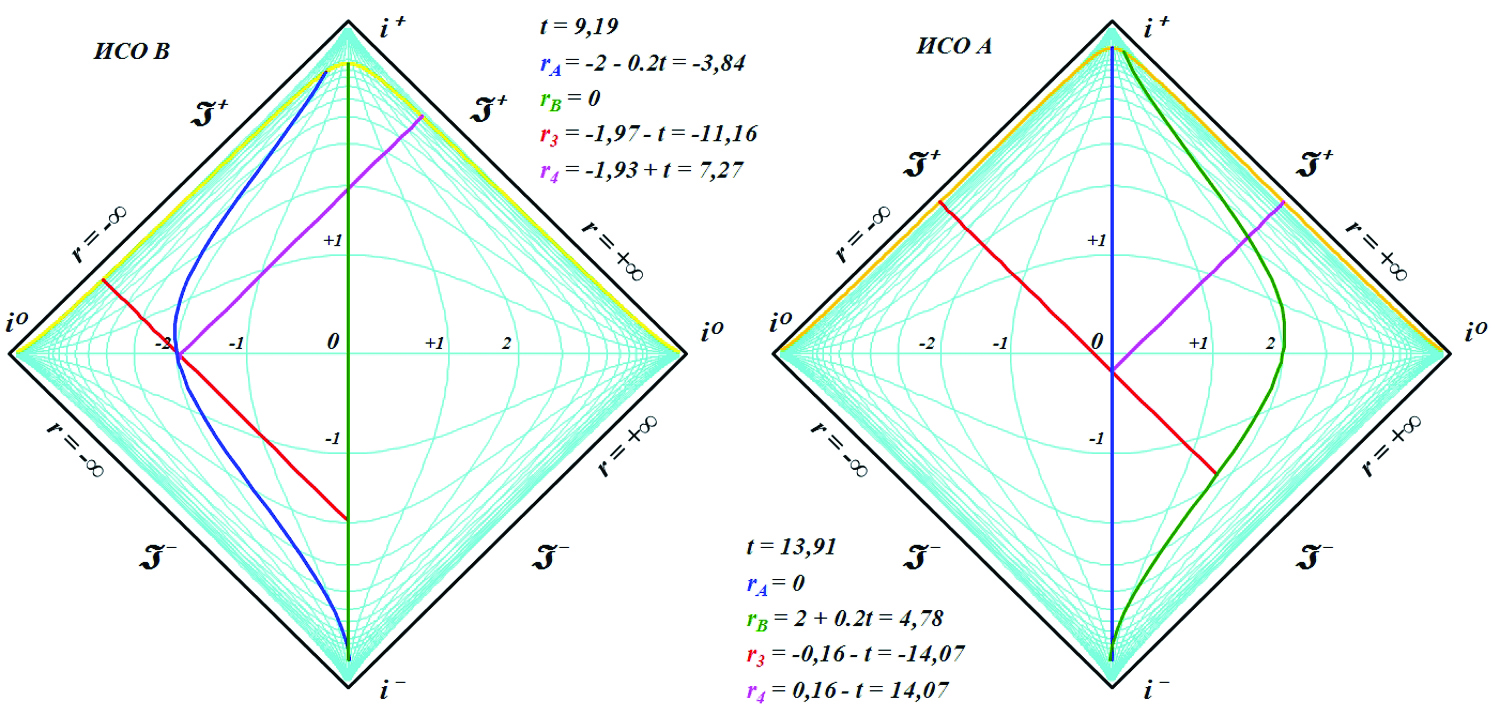
Рис.10. Диаграммы Пенроуза для двух ИСО, обменивающихся световыми сигналами. Анимация: http://samlib.ru/img/p/putenihin_p_w/diapen242/fig10.gif

Для проверки принципа относительности мы находим явным образом координаты всех известных нам точек излучения и получения сигналов. При этом мы знаем, что отрезки времени в ИСО В сократились по сравнению с отрезками в ИСО А. Мы можем вычислить и точку начала отсчета, когда две ИСО находились рядом, и коэффициент лоренцева сокращения.

После внесения в алгоритм программы этих точек и запуска программы мы видим, что всё в точности соответствует описанной картине в ИСО А. Сначала из ИСО В излучается луч r3, после получения которого в ИСО А излучается ответный сигнал r4. Все точки находятся на мировых линиях участников, никаких разрывов нет.