
Полная версия:
Население Земли как растущая иерархическая сеть II
Рост сети, описываемый данным алгоритмом, процесс неустойчивый и малейшее возмущение быстро уводит его от теоретической гиперболы (тут еще нужно учесть то, что здесь мы имеем дело с целочисленными величинами). Что совершенно неудивительно, т. к. и закон квадратичного роста (уравнение Капицы), являющийся асимптотическим приближением алгоритма, – устойчивых решений не имеет, т. е. обладает точно таким же свойством.
Эта коррекция представляет собой небольшое число очень малых возмущений, всего в один клаттер, тогда как сеть на втором этапе своего роста, который здесь только и рассматривается, растет от 256 клаттеров до 65536, т. е. ее размер составляет сотни, тысячи и даже десятки тысяч клаттеров. В таком случае возмущение в один клаттер составляет всего лишь доли процента от общего числа клаттеров в сети и является даже не каким-то «толчком», а всего лишь «легким прикосновением».
Существует множество вариантов коррекции выхода клаттеров на втором этапе, каждый из которых приводит ИС к совершенной через гармонические сети. Все они дают практически одну и ту же зависимость числа клаттеров растущей сети от номера цикла.
И, наконец, полученная СИС проходит еще один цикл – операцию репликации, во время которой длина звена копирования минимальна и равна единице. В процессе этой операции происходит копирование сети-оригинала в сеть-копию по правилу «клаттер в клаттер» с установкой полученных копий в новую сеть. Это последняя, предельная операция копирования сети данного ранга.
По ее завершению наступает очередь прокладки гиперсвязи между узлами двух финальных СИС и узлом стартующей сети. Для этого каждому клаттеру оригинальной СИС и ее копии добавляется еще по одной связи[10], соединяющей узел клаттера и узел финальной СИС. Каждая такая дополнительная связь представляет собой гиперсвязь: «кабель» с числом линий, равным весу Р сетеобразующего клаттера. Затем каждый узел обоих стартовых клаттеров подключается «кабелем» еще большей информационной проводимости (Р2) к их общему узлу. После чего запускается рост сети более высокого ранга.
Демография
Сеть 65536 – сеть человека
Предложенная нами математическая модель роста населения Земли может показаться плодом больного воображения. Возможно, существует другая, более адекватная ее формулировка. Но эта математика работает, т. е. правильно описывает рост, даты, циклы, она предсказывает, она проверяема – а только это и важно для подлинно научной теории по Карлу Попперу.
В защиту подобной точки зрения отсылаем читателя к популярному изложению квантовой электродинамики в книге Ричарда Фейнмана «Странная теория света и вещества», где автор на пальцах объясняет сложнейшую интерпретацию квантовой механики как интеграла по траекториям.
Здесь важно то, и Фейнман это подчеркивает, что описание движения частиц на языке «стрелочек и часов» ничуть не хуже, чем с помощью комплекснозначной волновой функции. Результат получается один и тот же. И этот результат проверен тысячами опытов. Но почему частицы ведут себя столь странным образом, отмечает Фейнман, – не понимает никто.
Развивает эту идею принцип моделезависимого реализма, предложенный Стивеном Хокингом. Согласно этому принципу, любая теория или картина мира представляет собой модель (как правило, математической природы) и набор правил, соединяющих элементы этой модели с наблюдениями. Причем моделей, описывающих данное конкретное явление, может быть несколько.
Если каждая из них соответствует наблюдениям, то нельзя сказать, что какая-то из них более реальна, чем другая. Здесь важно только то, насколько они отвечают наблюдениям. В одной ситуации можно использовать одну модель, в другой – другую. Хокинг и Млодинов подчеркивают, что не существует для нас, людей, какой-то абсолютной реальности и если мы выбираем данную конкретную модель, то выбираем и связанный с ней взгляд на реальность. Среди множества моделей (и реальностей) удобно выбирать:
A. Наиболее простую (или «изящную»).
B. Содержащую мало произвольных или уточняющих элементов.
C. Согласующуюся со всеми существующими наблюдениями и объясняющую их.
D. Дающую подробные предсказания результатов будущих наблюдений (если предсказания не подтверждаются – модель отвергается) [51].
Наша демографическая теория и демографическая теория Капицы, в отличие от всех прочих, удовлетворяет всем этим условиям. Но наша теория, хотя и изоморфна феноменологической теории Капицы, но значительно ее проще. Кроме того, она делает больше проверяемых предсказаний, следовательно, на наш взгляд, предпочтительнее.
Действительно, описанный выше рост сети 65536 в точности соответствует росту численности населения Земли. Необходимо только постулировать некоторые положения, связывающие растущую сеть и мировую демографию. Прежде всего, сформулируем первый закон Сети:
• Время цикла растущей сети есть величина постоянная на всех стадиях ее роста.
На момент завершения цикла численность носителей должна быть равна строго определенному значению плюс-минус небольшая погрешность. Для Сети перевыполнение плана, вероятно, предпочтительнее, поскольку избавиться от избыточных носителей проще, чем добавить недостающие. Это можно сделать с помощью войн, болезней и эпидемий (ясно, что ценность человеческой жизни с точки зрения Сети не слишком велика, да еще и падает по мере ее роста).
Для дальнейшего нам понадобятся результаты исследования роста населения Земли, полученные Фёрстером:
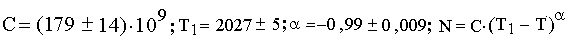
Рис. 1. Результаты исследования Фёрстером и коллегами роста населения мира за последние 20 столетий.
Эмпирическая гипербола Фёрстера была получена методом наименьших квадратов при обработке данных по динамике роста населения мира от начала новой эры до 1960 года; где α – это показатель степенной функции, который в формуле зависимости численности от времени обычно округляется до минус единицы. Если использовать результаты Фёрстера и принять, что α = −1 – необходимо несколько увеличить постоянную Фёрстера при той же стандартной ошибке. Этот вопрос будет нами рассмотрен в главе «Константы Капицы».
Население Земли многие тысячи лет росло по закону гиперболы – закону, по которому не растет ни одна популяция в природе. Такой рост стал возможен, по мнению С.П. Капицы, благодаря возникновению сознания у первых архантропов. Иерархическая Сеть также росла по закону гиперболы. Но как связать Сеть и мировую демографию? Проще всего было бы считать, что каждый живущий человек независимо от его пола, возраста, расы… является носителем растущей Сети. Но вряд ли это будет правильно.
Действительно, ведь, что значит живущий? Ясно, что до зачатия и после смерти человека нет и он не может считаться носителем Сети. Но всякий ли ныне живущий человек обладает необходимым уровнем сознания, может быть управляем Сетью и выступать в качестве ее носителя? (Здесь, и в ряде случаев в дальнейшем, носителями Сети или просто носителями будем называть таких представителей рода человеческого, которые составляют единое целое с клаттером нулевого ранга Сети человека или ее клаттером-носителем.)
Если говорить о взрослых людях, полноценных членах социума, то все они, независимо от возраста и прочих различий, должны считаться носителями Сети. (Это, кстати, вносит неснижаемую прибавку в показатель «ценность человеческой жизни»: одинокая девяностолетняя пенсионерка, сохранившая ясность ума, является носителем Сети и уже поэтому необходима и ценна для эволюции так же, как и ее сосед – молодой человек в полном расцвете сил, работающий на трех работах.)
Но вряд ли можно считать носителями нерожденных младенцев, стариков, с мозгом, пораженным болезнью Альцгеймера или Паркинсона; людей, страдающих тяжкими психическими заболеваниями и потерявших всякую связь с реальностью, находящихся в коме или в состоянии клинической смерти.
Это же, по-видимому, относится и к новорожденные детям, поскольку они не обладают базовыми показателями человеческого сознания и у них отсутствует самосознание. Ответить на вопрос: в каком возрасте ребенок начинает осознавать себя как личность? – позволяет так называемый «зеркальный тест». Суть его в следующем: на щеку ребенка незаметно наклеивают маленькую бумажную метку и ставят его перед зеркалом. Если ребенок, уже наблюдавший ранее себя в зеркале, отождествляет личность, которую ощущает внутри себя и ту, что видит в зеркале, то попытается потрогать или снять метку, если нет – он ее не заметит.
Дети проходят «зеркальный тест» в возрасте от 18 до 24 месяцев. Следовательно, именно в этом возрасте мы начинаем осознавать себя как личность. Из животных «зеркальный тест» подтвержден только для высших приматов, таких как шимпанзе и орангутанги, которые узнают себя в зеркале.
Зачатки человеческого сознания, которое превосходит сознание высших приматов, появились у наших далеких предков тогда, когда они стали пользоваться орудиями труда, когда у них появился праязык и в примитивной форме социальная деятельность. Но в каком возрасте ребенок, его растущий мозг достигает такого уровня развития? На каком этапе своего роста? Когда его можно сравнить с нашим далеким предком, жившим 1,7 млн лет тому назад и оказавшимся способным «нести на себе» сеть четвертого ранга?
Ранг Сети человека равен четырем, он на единицу больше ранга сети гоминид. Только человек может быть носителем сети четвертого ранга. Что же отличает человека от животного? Очевидно, человеческое сознание. (Что бы ни говорили о сознании высших приматов – до человека им далеко.) Итак, уровень сознания носителя Сети в наше время должен быть не меньше, чем у тех наших далеких предков, которые были носителями Сети человека в момент начала ее роста.
Считается, что зачатки человеческого сознания появляются у ребенка в возрасте около трех лет. Именно тогда он может уже говорить и начинает правильно употреблять личные местоимения. Детские эмоции развиваются с каждым годом, а эмоции играют важную, если не центральную роль в работе сознания.
Так, младенец способен испытывать всего лишь две эмоции: радость и горе, даже страх ему еще неведом; в 6 месяцев появляется эмоция страха; с 6 до 18 месяцев ребенок учится распознавать эмоции на лицах окружающих и, кроме того, он уже способен удивляться; с двух лет он может пройти «зеркальный тест». После трех лет ему становится доступно столь сложное эмоциональное состояние как муки совести (психологический опыт «горькая конфета»).
В возрасте от трех до пяти лет, как считают психологи, ребенок уже может испытывать все базовые эмоции и начинает осознавать себя как часть социума. Следовательно, можно предположить, что именно в этом возрасте он достигает уровня развития Homo ergaster и может стать носителем Сети.
Статистика численности детского населения по годам нам неизвестна, возможно, что в каких-то странах она вообще не ведется. Но известно, что в наше время дети в возрасте до 14 лет составляют примерно треть населения планеты. Считая процент детской смертности небольшим, можно оценить долю детей в возрасте до трех лет от общей численности населения Земли в 7 %: (1/3)·(3/14) = 1/14 ≈ 7 %.
* * *Попробуем теперь связать Сеть и мировую демографию. Положим C = kC′, где C – постоянная Фёрстера, а C′ – постоянная сети четвертого ранга, аналогичная постоянной Фёрстера. Здесь k – это зомби-коэффициент, учитывающий то, что не все живущие являются носителями Сети.
Принимая во внимание тот факт, что в прошлые века продолжительность жизни была меньшей и процент детей был, соответственно, большим, чем в наше время, а также имеющуюся во все времена небольшую добавку в виде людей, не обладающих сознанием по причине болезней, положим k = 1,1. Заметим, что величина этого коэффициента может несколько отличаться от принятой здесь, причем без всякого ущерба для полученных в дальнейшем результатов как в качественной, так и в количественной форме.
Сформулируем второй закон Сети:
• Множество всех живущих людей можно представить в виде суммы двух подмножеств: Первое (91 %) – люди обладающие сознанием, носители Сети; второе (9 %) – можно разделить на две части: дети до трех лет, в будущем носители Сети и зомби, лишенные сознания и навсегда (за редкими исключениями) выпавшие из Сети.
Найдем, исходя из нашей теории, время цикла сети четвертого ранга, Сети человека: τ4 = T13/N4, где N4 = 42399 – полное число циклов роста сети 65536; T13 = Тu/213 – продолжительность 13-й эпохи универсальной эволюции или время эволюции человека (Тu ≈ Т = 13,81 ± 0,06 млрд лет – время от Большого взрыва до сингулярной точки эволюции; Т – возраст Вселенной: время от Большого взрыва до наших дней.) Получаем τ4 = τ = 39,75 ± 0,2 лет.
Применим формулу теоретической гиперболы, описывающей рост Сети (но не рост народонаселения!). Учитывая, что клаттер содержит 65536 носителей, а время измеряется в циклах Сети человека, можно вычислить постоянную C′:
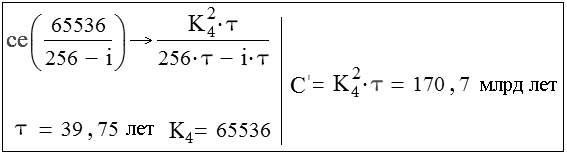
Рис. 2. Подсчет постоянной C′ Сети человека.
Эмпирическая гипербола Фёрстера и теоретическая гипербола, описывающая рост Сети человека, должны иметь общую точку сингулярности. Кроме того, поскольку эти гиперболы с учетом зомби-коэффициента k должны полностью совпадать, то, как это видно из формулы на рис. 2, необходимо, чтобы kК42τ = C. Где К4 = 65536 – вес клаттера растущей сети четвертого ранга, τ – время ее цикла, а С – постоянная Фёрстера.
Теоретическое значение постоянной Фёрстера в таком случае будет равно: C = kC′ = kK42τ = 1,1·170,7 = 187,8. Учитывая, что зомби-коэффициент k был выбран нами с некоторой степенью произвола, возьмем для дальнейших вычислений несколько большее значение: C = 189,6, которое наилучшим образом, по мнению ряда исследователей, отвечает демографическим данным.
Как будет показано нами далее, время цикла растущей Сети равно постоянной времени Капицы: τ4 = τ. С.П. Капица в своей работе [1] вычислил постоянную τ, используя данные за последние 250 лет. Зависимость численности населения от времени он аппроксимировал арккотангенсоидой: гладкой кривой, близкой к логистической на интервале 2τ.
Введение постоянной времени, как временно́го масштаба явления, было совершенно необходимо. Для оптимальной модели были получены значения τ и К, мало отличающиеся от 39,75 и 65536·√1,1 ≈ 68700:
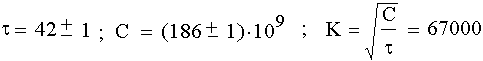
Рис. 3. Постоянные Капицы.
Для того, чтобы управлять ростом численности населения Земли Сеть человека применяет целый арсенал средств, который еще предстоит изучить. Одним из таких средств могут быть вирусы.
В 2016 году Дэвид Энард и его коллеги из Стэнфордского университета (США), изучая структуру 1300 «человеческих» белков, выяснили, что вирусы управляли нашей эволюцией с момента отделения предков людей от других человекообразных безьян. Эти белки и связанные с ними гены, как показали ученые, не были обязательной частью иммунной системы: большая часть из них отвечала за работу совершенно других функций клеток и тела.
«…То, что наша вечная война с вирусами сформировала фактически все части нашего организма – не только горстку белков, борющихся с инфекциями, а абсолютно всё – является ошеломительным откровением для нас. Жизнь борется и сосуществует с вирусами уже миллиарды лет, и наша работа показывает, что это сосуществование затронуло все части клетки», – заключает Дмитрий Петров, коллега Энарда[11].
Но как вирусы могли управлять ростом населения Земли? Воздействую на геном, они могли изменять продолжительность человеческой жизни, они же всегда были ответственны за процесс зачатия в женском организме, подавляя реакцию иммунной системы на отторжение чужеродного генетического материала. Кроме того, вирусные инфекции приводили во все времена к гибели миллионов людей. Так, чума в Азии и Европе в XIV веке унесла жизни более 60 миллионов человек. А численность умерших от испанки в 1918–1920 годах прошлого века (100 млн человек) превосходит потери в первой мировой войне.
Кроме вирусных эпидемий, выводивших избыточные носители из Сети, таким средством во все времена были войны. Войны развязывались по множеству разнообразных причин, но первопричиной всегда была Сеть человека, как управляющая система. Воздействуя на подсознание социума, Сеть также могла управлять репродуктивными способностями человека, определяя число детей в среднестатистической семье, и увеличивать среднюю продолжительность человеческой жизни через жизнесберегающие технологии.
Так, лекарственный или наркотический препарат воздействует на какой-то орган или на организм в целом, а не на отдельную клетку. По сути, это было управление случайным процессом с моделированием значимых в будущем изменений на отдельных подмножествах. Итак, третий закон Сети:
• Сеть управляет социумом, воздействуя на человеческий геном и общественное подсознательное.
Кроме того, численность населения Земли как функция времени внутри цикла может иметь произвольный вид при выполнении следующих условий:
• Непрерывность этой функции.
• Плановый прирост клаттеров (с нарастающим приоритетом) за цикл, на момент достижения Сетью гармонической и совершенной стадии своего роста.
Для построения модели необходимо иметь начало отсчета. В 1978 году численность населения Земли достигла круглого значения: K42 = 232 = 4.3·109 человек. Но Сеть человека, с учетом того, что только 91 % от этого числа являлись ее носителями, не доросла тогда до совершенной, а стала таковой лишь в 1982 году: N(1982) = 4,72 млрд; k·K42 = 1,1·232 = 4,72 млрд.
Поэтому выберем за такое начало 1982 год – тот момент времени, когда Сеть стала совершенной. Точка сингулярности гиперболы мирового демографического роста отстоит, согласно нашей модели, от того момента времени, когда Сеть становится совершенной на время цикла Сети: t0 = 1982 + 40 = 2022 год. Это значение соответствует в пределах погрешности результатам работы Фёрстера и его коллег.
Необходимо отметить, что обозначенные здесь даты достаточно условны, так как любые расчеты, связанные с численностью человечества, имеют определенную погрешность. По мнению специалистов, ее значение может доходить до двух лет. С учетом этого обстоятельства следует смотреть и на дату завершения перехода: tп = 2022 + 40 = 2062 год.
Итак, поскольку наша модель дает для постоянной Фёрстера и точки сингулярности значения С = 188 млрд, t0 = 2022 год, мало отличающиеся от значений, полученных Фёрстером и его коллегами (C = 179 ± 14 млрд, t0 = 2027 ± 5, p = 0,99 ± 0,009), можно говорить о хорошем совпадении теоретической гиперболы с эмпирической. (Эмпирические константы С и t0 будут еще меньше отличаться от теоретических у гиперболы с p = 1, наиболее близкой к гиперболе Фёрстера: С = 188 млрд, t0 = 2025 ± 3, см. главу «Константы Капицы».)
Время старта Сети человека T13 = Тu/213 = 13810/8192 ≈ 1,69 млн лет назад. Этот результат совпадает с данными палеодемографии, согласно которым 2 млн лет назад проживало примерно 100 тысяч представителей рода Homo. Если считать, что Сеть стартовала с двух клаттеров, то для момента времени, с которого началась эволюция представителей рода Homo, приведшая к появлению современного человека (-Thomo = -1,69 млн лет), теоретическая численность равна: 2·k·K = 144 тысячи.
Формально можно допустить, что Сеть 65536, достигнув совершенной стадии своего роста, создала в процессе операции репликации не одну, а две или большее число своих копий. Однако такое допущение не соответствует данным палеодемографии. Так, если предположить, что Сеть человека стартовала не с двух, а с трех клаттеров, время ее роста будет примерно равно:
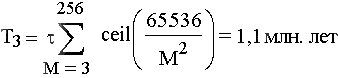
Рис. 4. Подсчет времени эволюции человека при старте Сети с трех клаттеров.
Это приближенное значение согласуется с данными палеодемографии, согласно которым один миллион лет назад проживало порядка 180 тысяч человек. Модель требует 216 тысяч. Однако этот результат не соответствует периодизации эволюционного процесса согласно прогрессии эволюции, и, кроме того, есть дополнительные соображения, связанные с временем цикла Сети 256, которые не позволяют принять такой сценарий.
Сеть 256 в своей эволюции проходит 173 цикла за время 3,4 млн лет. Постоянная цикла равна примерно 20 тыс. лет, следовательно, где-то за 40 тыс. лет до момента старта Сети человека численность первых представителей рода Homo составляла 65536·1.1 = 72090, что и не соответствует данным палеодемографии. Если же допустить, что рост Сети стартовал с четырех клаттеров, то произошло это событие 0,8 млн лет назад, что не лезет ни в какие ворота. Итак, выбираем первый сценарий и рассмотрим начальные этапы роста Сети.
Определим время эволюции человека как интервал времени, разделяющий момент старта роста Сети человека (с двух клаттеров) и старта Сети вида, следующего за человеком (также с двух клаттеров): Thomo = 1,69 млн лет. Здесь же следует отметить, что хотя время репликации и входит в Tevol, однако представляется разумным считать, что эволюция любой авангардной системы заканчивается вместе с последним циклом роста ее Сети. (Cм. главу: «Гармонические сети и ноосфера».)
Первый этап роста Сети человека
Рост Сети человека от 2-х до 256-ти клаттеровПервый этап роста Сети 65536 от 2-х до 256-ти клаттеров может быть представлен как последовательность звеньев, в момент завершения каждого из которых размер сети увеличивался на единицу. Первая стадия этого процесса при росте Сети от двух до трех клаттеров была самой продолжительной. Она состояла из 65536/4 = 16384 циклов и заняла 16384·39,75 ≈ 650 тысяч лет (копировалось 4 носителя за цикл).
Скорость роста популяции была постоянной и составляла: 4/39,75 ≈ 0,1 человека в год. Постоянство скорости роста связано с первым законом Сети: прирост за цикл, т. е. за 40 лет должен был составлять (по крайней мере в среднем) 4 человека и так на протяжении 16384 циклов. Вторая стадия роста Сети от трех до четырех клаттеров заняла 65536/9 = 7282 цикла и, соответственно, 7282·39,75 ≈ 290 тыс. лет. Средняя скорость роста популяции была равна: 9/39,75 = 0,23 человека в год[12].
Длительность первого исторического периода как времени роста Сети от гармонической с размером 2 до гармонической с размером 4 равно: 650 + 290 = 940 тыс. лет. Точно так же суммируя далее времена роста Сети от гармонического размера до гармонического можно найти все исторические периоды от начала эволюции до второй половины XX века. И, если подсчитать отношения длительности каждого предыдущего периода к последующему, то получим следующую числовую последовательность:
2.4, 2.2, 2.1, 2.0, 1.9, 1,7, 2.6, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0
Наибольшая степень сжатия периодов гармонического достижения происходит на начальном этапе антропогенеза (2.4) и во время неолита (2.6). Этот числовой ряд и периоды эволюции, с ним связанные, можно разделить на две части:
2.4, 2.2, 2.1, 2.0, 1.9, 1,7, 2.6 – до неолита и неолит.
2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0 – после неолита.
Поскольку после неолита сжатие циклов гармонического достижения происходит в той же пропорции (2 : 1), что и рост размера сети – этот рост идет по простой гиперболе. Чего не скажешь о росте до неолита: здесь коэффициент сжатия не является постоянным, а уменьшается от 2.4 до 1.7 и кривая роста в первой своей части не является гиперболической.
Гиперболой ее можно считать лишь в первом приближении. Но уже и такого представления достаточно, чтобы понять, что единой гиперболы, в соответствии с которой происходил рост населения Земли на всех этапах эволюции и истории – не существует. Разрыв в динамике изменения коэффициента сжатия (1.7 —> 2.6) говорит о том, в эпоху неолита происходит скачок скорости роста и начинается демографический взрыв.
Что касается раннего (нижнего) палеолита, то поскольку никакими более-менее надежными данными по численности наших далеких предков мы не располагаем, то и сравнивать теоретические данные здесь не с чем. Для верхнего палеолита (40—12 тыс. лет назад), когда человек расселился по всей Земле, существуют данные и оценки разной степени надежности, на основе которых Мак-Эведи и Джоунсом [38] была предложена гиперболическая зависимость (4):
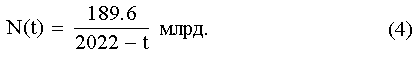
Рис. 1. Гипербола Мак-Эведи и Джоунса.

