
Полная версия:
Население Земли как растущая иерархическая сеть II
С.П. Капица ввел две константы τ и К вместо одной С, в результате чего была получена хорошая аппроксимация зависимости численности населения мира от времени на всех этапах роста, включая демографический переход. Были получены новые результаты, важнейший из которых − принцип демографического императива. Этот принцип, в отличие от ресурсного мальтузианского, утверждает, что рост численности населения Земли на протяжении всей истории человечества зависел только от самой этой численности и не зависел ни от каких ресурсов.
Феномен квадратичной зависимости скорости роста численности населения (ежегодного мирового естественного прироста) от численности С.П. Капица объясняет системностью человечества и информационной природой развития, присущей только человеку. Но человечество долгое время не представляло собой системы, и рост населения в Европе, Америке, Азии… происходил независимо.
Тогда в чем причина этой квадратичной зависимости? – Непонятно. Константы τ и К были введены С.П. Капицей при анализе динамики роста населения Земли за последние 250 лет, включая начало демографического перехода, и смысл их до сих пор остается непонятным. Сам он определил эти постоянные так:
1. Константа τ = 42 года − это время, определяемое внутренней, предельной способностью системы человечества и человека к развитию.
2. Константа К = 67000 – безразмерная величина, которая является центральной в его теории; она задает численность группы людей, которая определяет характер коллективного взаимодействия.
Но какой временной масштаб задает постоянная времени τ? Связана ли она со средней продолжительностью жизни? Почему длительность демографического перехода равна 2τ? А константа К, так близкая к круглому числу 216, в чем ее смысл? Таким образом, теория Капицы, с одной стороны, позволила ответить на ряд важных вопросов, а, с другой стороны, как это часто бывает в науке, породила новые.
Математика
Приведем элементарные определения, которые легко поймет и ученик старших классов, но без которых невозможно уяснить суть предлагаемой гипотезы.
Центральное место в теории занимает сеть. Под сетью будем понимать граф, в котором все узлы соединены между собой ненаправленными отрезками: «каждый с каждым». Например, сеть, состоящая из пяти узлов, содержит десять связей.
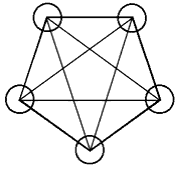
Рис. 1. Сеть, состоящая из пяти узлов, число связей равно 10.
Гармоническая сеть содержит число узлов, равное двойке в некоторой целой степени – 2n, например: 2,4,8,16… (n = 1,2,3,4…).

Рис. 2. Гармоническая сеть, содержащая 8 узлов; число связей равно 28.
Совершенная сеть содержит число узлов, равное двойке, в показателе которой стоит тоже двойка в степени R: 22^R. Где R – ранг сети. Например: 2,4,16,256,65536… (R = 0,1,2,3,4…).

Рис. 3. Совершенная сеть второго ранга, содержащая 16 узлов; число связей равно 120.
Совершенная иерархическая сеть (СИС) ранга R – это совершенная сеть, узлы которой (назовем их клаттерами) – это СИС ранга R − 1. Чтобы рекурсия заработала введем СИС наименьшего ранга: самый нижний уровень иерархии, атом сетестроения. Это сеть ранга нуль, состоящая из двух узлов, соединенных связью. В дальнейшем будем считать, что за каждым узлом сети ранга нуль закреплен ее носитель-человек.
Носитель сети обеспечивает ее эволюцию, рост и функционирование. В чем разница между узлом и носителем? Узел сети ранга нуль (или узел-носитель) в приложении этой модели к процессу роста населения Земли есть величина постоянная, тогда как носитель-человек – это живущий и обладающий сознанием человек, временно «прикрепленный» к узлу и постоянно сменяющийся в процессе ее роста. (Далее, для краткости изложения будем отождествлять узел сети ранга нуль и ее носителя-человека.) Каждый узел сети ранга нуль также представляет собой иерархическую сеть, истоки которой теряются в глубинах микромира, но в данной упрощенной модели считаем его бесструктурной, неопределяемой через нижние уровни и неделимой далее структурной единицей иерархической сети.
Пример: если ранг сети равен трем (R = 3), то СИС содержит 256 носителей или 16 клаттеров; каждый ее клаттер – это СИС ранга 2, содержащая 4 клаттера ранга 1, каждый из которых, в свою очередь, содержит два клаттера ранга 0, каждый из которых включает два носителя.
Гармоническая иерархическая сеть (ГИС) ранга R – это гармоническая сеть, узлами которой являются СИС ранга R. Несовершенная иерархическая сеть или просто иерархическая сеть ранга R − это сеть, сетеобразующий клаттер которой – это СИС ранга R, а общее число ее клаттеров не равно двойке в некоторой степени (т. е. она не является гармонической).
Число носителей в клаттере ИС назовем весом клаттера, а полное число клаттеров в сети – ее размером. Например, ИС ранга 4 (R = 4), состоящая из десяти клаттеров, включает десять клаттеров, каждый из которых имеет вес 65536, т. е. содержит 65536 носителей. Если число клаттеров иерархической сети четвертого ранга максимально и равно весу ее сетеобразующего клаттера, т. е. 65536, то она превращается в совершенную иерархическую сеть пятого ранга, число узлов (носителей) которой равно 655362 = 4 294 967 296. Это число равно весу клаттера пятого ранга.
Растущая ИС − это ИС, число клаттеров которой растет согласно некоторому алгоритму. Рост сети будем связывать с операцией копирования сетью самой себя, т. е. с ее самокопированием. Процесс самокопирования сети может быть представлен в виде последовательности циклов.
Цикл − это такой этап самокопирования сети, когда копируются все клаттеры, имеющиеся в сети на момент входа в него. (Время цикла в приложении этой модели к росту населения Земли считается постоянным.) Копирование происходит с помощью носителей. Носители служат также для поддержания узлов сети и связей между ее клаттерами (принимаем, что один носитель способен поддерживать только один узел или только одну связь). В нашей модели узел сети – это сеть, не имеющая ранга, связанная с человеком.
Алгоритм копирования выбираем такой:
1. Рост сети начинается с двух клаттеров.
2. Связи и узлы растущей сети копируются носителями: один носитель – на связь клаттера, один – на его узел.
3. Когда число откопированных носителей становится равным числу носителей в сетеобразующем клаттере, собирается новый клаттер. Затем он устанавливается в сеть, т. е. прокладываются связи между ним и другими клаттерами сети. В очередь на копирование в текущем цикле такой новоиспеченный клаттер уже не ставится.
Рост сети идет в ускоряющемся темпе, т. к. число связей каждого сетеобразующего клаттера увеличивается на единицу после установки в нее очередного дочернего клаттера. Такой рост условно можно разделить на три этапа:
1. Рост от двух клаттеров до корня квадратного из веса сетеобразующего клаттера.
2. Дальнейший рост ИС до совершенной.
3. Репликация − предельная операция самокопирования, когда собирается единичная копия полученной совершенной сети.
Затем между полученной СИС и ее копией прокладывается связь и стартует сеть более высокого ранга. Поясним это на примере. Пусть сеть с весом сетеобразующего клаттера, равным 65536, т. е. сеть четвертого ранга, начинает свой рост с двух клаттеров. Копируем носителями узел каждого клаттера и входящую в него связь. Связь одна, узел всегда один.
За цикл копируются 4 носителя. Всего потребуется 65536/4 = 16384 цикла, чтобы собрать первый клаттер. После установки его в сеть имеем три клаттера, за цикл копируются уже 9 носителей. Всего циклов будет 7282. Получаем четыре клаттера. И так далее. Процесс идет с нарастающей скоростью.
Когда размер сети дорастет до 256 клаттеров – это корень квадратный из 65536 – впервые за цикл с нуля будет собран клаттер. Дальнейший рост ИС носит взрывной характер. Если до этого момента сеть проходит 42142 цикла, то после него ее рост до совершенной, т. е. от 256-ти до 65536-ти клаттеров происходит всего за 255 циклов. Все это, конечно, строго доказывается.
И, наконец, растущая сеть достигает совершенства, предложенный алгоритм ее роста не может больше работать (дальнейшая прокладка связей между клаттерами становится невозможной), поскольку все 65536 носителей в сетеобразующем клаттере оказываются занятыми: 65535 − на связи, один − на узел клаттера.
Тогда и наступает очередь операции репликации, когда происходит копирование полученной совершенной сети по правилу «клаттер в клаттер», т. е. последовательное клонирование клаттеров итоговой сети с немедленной установкой клаттеров-клонов в новую сеть. В нашей модели, как и в модели Капицы, демографический переход, который соответствует операции репликации Сети человека, занимает два цикла характерного времени. В таком случае полное время роста сети 65536 в единицах характерного времени равно: 42142+255+2 = 42399. Сеть 4 294 967 296 (65536 в квадрате) стартует с двух клаттеров.
Демография
Описанный выше рост сети 65536 в точности соответствует росту численности населения Земли. Необходимо только постулировать следующие положения:
1. Время цикла растущей сети есть величина постоянная на всех стадиях ее роста.
2. Каждый обладающий сознанием человек, независимо от пола, возраста, расы… независимо от его месторасположения в пространстве является носителем сети. Прирост численности таких людей за цикл соответствует приросту числа клаттеров.
3. Сеть управляет социумом, воздействуя на общественное подсознательное.
4. Сама же сеть отождествляется с суперсознанием, которое управляет человеческим социумом с помощью целого арсенала средств, который еще предстоит изучить.
При этом человек предстает, с одной стороны, как «носитель» иерархической сети. А, с другой – как индивидуум, обладающий собственным сознанием, причем сознание узла-носителя не подвластно ему и не контролируемо.
Сколь бы чудовищным ни казалось подобное представление, судить об истинности гипотезы нужно по ее соответствию экспериментальным данным. Но здесь все в полном порядке. Время цикла сети легко вычисляется из постоянной Фёрстера, которая была получена при обработке большого массива данных за последние два тысячелетия.
Оно оказывается равным примерно 40 годам, что практически не отличается от постоянной времени Капицы. Она принимала у него значения в интервале 41–45 лет в процессе «эволюции» теории Капицы. Безразмерная константа К, смысл которой у С.П. Капицы остается непонятным, варьируется им в интервале 62000 – 67000. Здесь же − это вес клаттера сети человека равный 216 = 65536.
Предлагаемая нами гипотеза имеет только одну постоянную τ = 40 лет, а все значения важных для описания эволюции человека, мирового демографического и исторического процесса величин (дат и численности) вытекают из идеальной математической схемы.
Сеть человека стартовала с двух клаттеров, что соответствует числу носителей равному 2·65536 = 131072. Полное число циклов ее роста, согласно теории, равно 42399. Умножив эту величину на τ, получим 1,69 млн лет. Это время эволюции человека. Оба эти результата полностью соответствуют данным палеодемографии, согласно которым 2 млн лет назад численность популяции Homo sapiens составляла примерно 100 тысяч человек: подсчитано по числу стоянок первобытного человека на Африканском континенте.
К моменту начала неолита сеть прошла 42142 цикла и выросла до 256 клаттеров. Согласно теории в этот момент времени, 8 тысяч лет до н. э. (1982 − 255τ), численность населения Земли достигла значения 256·65536 = 16,8 млн человек, что также соответствуют историческим данным.
Взрывной гиперболический рост численности после неолита полностью объясняется теорией. Гипербола Хорнера сливается с теоретической гиперболой. В 1982 году сеть 65536 достигает совершенства, что соответствует числу носителей К2 = 655362 = 4,3 млрд человек – эволюция человека заканчивается. Последний цикл роста сети: 1942–1982 гг. приводит к удвоению населения мира, что соответствует и теории, и демографическим данным. Можно доказать, что сеть любого ранга на последнем цикле своего роста удваивает число носителей.
Демографический переход соответствует «операции репликации» Сети человека. В результате этой операции будет построена стартовая конфигурация сети 5-го ранга, состоящая из двух клаттеров. Каждый из них будет содержать 232 = 4,3 млрд человек. Согласно модели Капицы и нашей модели, демографический переход занимает два цикла характерного времени: 2·40 = 80 лет. По нашим подсчетам он закончится в 2062 году. Численность населения Земли в этот момент времени достигнет значения, равного примерно 9 млрд человек и многие тысячелетия меняться практически не будет. (Рост сети пятого ранга, сети post Homo, так же как и рост Сети человека на первых этапах ее роста, будет совершенно незаметен. См. «Эволюция после человека».)
Драматизм ситуации заключается в том, что все мы находимся «внутри» первого цикла демографического перехода. В 2000 году население мира достигло значения 6,1 млрд чел., а скорость роста – величины 87 млн чел. в год и начался ее спад.
При таких темпах роста население Земли к 2022 году, т. е. к концу первого цикла перехода, составило бы N = 6,1 + 0,087·21,5 = 7,97 млрд человек. Так как скорость роста численности продолжает уменьшаться, то для достижения численности значения, равного 9 млрд и ее стабилизации на этом уровне, учитывая, что время роста сети «квантовано» и измеряется целым числом циклов, – демографической системе потребуется еще один цикл.
Следовательно, при таком сценарии переход закончится в 2062 году, после чего мировая демографическая система войдет в состояние гомеостаза, при котором численность населения мира многие тысячи лет меняться практически не будет.
Уравнение Капицы, описывающее гиперболический рост населения Земли, может быть получено из алгоритма растущей сети в предположении, что за цикл собирается количество клаттеров, значительно меньшее размера сети.
История
Антропологические и исторические данные свидетельствуют о циклической природе развития человека. Причем длительность этих циклов с течением времени сокращается. Если время измерять в логарифмическом масштабе – шкала антропологических и исторических циклов становится равномерной. Как все это можно объяснить?
Об этом пишет в своей книге «Пути истории» историк И.М. Дьяконов, а С.П. Капица указывает на существование одиннадцати временны́х периодов в истории эволюции человека. Однако понимания причины цикличности достигнуто не было.
Предлагаемая нами модель такое объяснение дает. Действительно, Сеть человека растет от 2-х до 65536-ти клаттеров. Гармоническая сеть содержит 2K носителей. Следовательно, Сеть человека в процессе эволюции проходит 16 гармонических стадий своего роста с числом носителей 217,218,…224….232. С каждой такой стадией можно связать соответствующий этап эволюции и развития человечества как системы. Соответственно, имеется 15 периодов становления ноосферы. Эти этапы подробно рассмотрены в главе «Гармонические сети и ноосфера». Причем теория хорошо соответствует как антропологическим, так и историческим данным.
Зная постоянную цикла, легко подсчитать момент начала каждого периода и его длительность. Если выписать отношения длительности каждого последующего периода к предыдущему, получим следующий ряд:
0.42, 0.45, 0.48, 0.50, 0.52, 0.60, 0.39, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5
Скачок в этой последовательности приходится на неолит, когда степень сжатия периодов эволюции и истории была максимальной. В это переломное время происходит скачок скорости роста численности, т. е. первая производная от численности по времени претерпевает разрыв.
На кривой роста численности населения Земли есть только три такие точки. Кроме неолита – это момент начала эволюции (старт сети 65536) и момент ее конца: завершение второго цикла демографического перехода.
Неолит − посередине пятнадцати исторических периодов, т. е. он по счету восьмой. Причем, в отличие от неолита, скачок скорости роста в этих «граничных» точках отрицательный: она падает до нуля за ничтожное по историческим меркам время.
С момента начала эволюции до неолита сжатие периодов эволюции и истории хотя и замедлялось, но замедлялось незначительно, оставаясь близким к геометрической прогрессии; после неолита – это уже в точности геометрическая прогрессия со знаменателем ½.
Историки давно заметили, что мировой исторический процесс происходил с удивительной синхронностью на разных исторических этапах, в разных странах, регионах, частях света. Если исходить из предлагаемой здесь гипотезы, то и это явление не вызывает удивления.
Действительно, человечество в целом в разные времена все целиком находилось «в сети» и эволюционировало синхронно с ее ростом независимо от пространственного расположения носителей. Именно этим и объясняется синхронизм исторического процесса.
* * *Дополнительно хотелось бы отметить следующее. Возможно, что представленная здесь модель роста населения Земли покажется чистой выдумкой, не имеющей к реальному демографическому и историческому процессу никакого отношения. Но дело в том, что выбранный алгоритм настолько прост, что для его описания требуется всего несколько сотен байт на алгоритмическом или несколько строчек на естественном языке.
При этом он позволяет правильно описывать как количественно, так и качественно динамику роста: сам гиперболический рост, значение численности в момент его начала, а также положение этого начала на оси времени, времена начала неолита и перехода, значение численности в эти моменты времени.
Кроме того – и это стало неожиданным даже для самого автора – модель хронологически точно описывает временны́е границы пятнадцати циклов эволюционного и исторического развития. Восемь сокращающихся по закону прогрессии со знаменателем ½ глобальных исторических циклов от неолита до второй половины ХХ века настолько точно соответствуют историческим данным, что С.П. Капица в последней своей работе [21] отказался от прежней периодизации по закону прогрессии со знаменателем 1/3 и принял нашу.
С помощью этого же алгоритма можно определить время эволюции человека: 1,69 млн лет, а в применении его к процессу роста сети пятого ранга – и возраст Вселенной с точностью до пяти значащих цифр: 13,805 млрд лет (см. параграф «Цикл 160 минут и возраст Вселенной»).
В таком случае предложенную модель можно было бы рассматривать (независимо от ее истинности) как простую и эффективную схему, позволяющую систематизировать многочисленные данные по мировой демографии и (на заключительных ее этапах) Большой истории. Но вопроса о том, почему это стало возможным, почему такая простая модель столь точно соответствует действительности, почему она вмещает в себя такой большой объем информации, случайно ли? – все равно не избежать.
Эволюция
Время эволюции человека равно произведению постоянной времени Капицы (времени цикла сети человека) на полное число циклов сети 65536. Thomo = 39,76·42399 = 1,69 млн лет. Зафиксируем в будущем точку на оси времени, отстоящую от настоящего на 1,69 млн лет. Эта точка, как мы сейчас покажем, отмечает недостижимую сингулярную точку эволюции.
В момент Большого взрыва стартовал глобальный эволюционный процесс. С каждой эпохой эволюции была связана своя сетевая структура и соответствующая ей авангардная система эволюции. Всего таких эпох − шестнадцать.
Момент начала эволюции следующей по счету авангардной системы и старта роста соответствующей сети – это середина отрезка на оси времени, соединяющего начало эволюции текущего авангарда и точку сингулярности. Иначе говоря, эти времена определяются последовательностью шагов по оси времени, в которой каждый следующий шаг вдвое короче предыдущего.
Следовательно, прогрессия универсальной эволюции, так же как прогрессия мирового исторического процесса, – это геометрическая прогрессия со знаменателем ½. Далее мы покажем, что по такому же закону, в соответствии правилом Тициуса–Боде, размечена и планетарная зона Солнечной системы[4].
Время Большого взрыва согласно современным научным данным равно 13810 млн лет. Оно задает момент начала ядерной эволюции. Отсчет времени ведем от точки сингулярности, находящейся в будущем и отстоящей от настоящего на 1,69 млн лет, а затем пересчитываем на настоящее время (вычитаем 1,69 млн лет):
• начало химической эволюции 13810/2 = 6905 млн лет от точки сингулярности;
• начало эволюции прокариот 6905/2 = 3453 млн лет от точки сингулярности;
• начало эволюции эукариот 3453/2 = 1726 млн лет от точки сингулярности;
• начало эволюции многоклеточных 1726/2 = 863 млн лет = 861 млн лет назад;
• начало эволюции позвоночных 862/2 = 431 млн лет = 429 млн лет назад;
• начало эволюции ящеров 431/2 = 215,5 млн лет = 214 млн лет назад;
• появление плацентарных млекопитающих 215,5/2 = 107,7 млн лет = 106 млн лет назад;
• появление первых приматов 107,7/2 = 53,9 млн лет = 52,3 млн лет назад;
• появление предков человекообразных обезьян 53,9/2 = 27,0 млн лет = 25,3 млн лет назад;
• появление африканских гоминоидов 27,0/2 = 13,5 млн лет = 11,8 млн лет назад;
• появление первых гоминид 13,5/2 = 6,75 млн лет = 5,06 млн лет назад;
• появление линии представителей рода Homo, ведущей к современному человеку: 6,75/2 = 3,38 млн лет = 1,69 млн лет назад;
В итоге получим ряд (млн лет):
0, 1.69, 5.06, 11.8, 25.3, 52.3, 106, 214, 429, 861, 1724, 3451, 6903, 13810.
Эта последовательность задает времена начала эпох эволюции от старта эволюции вида, следующего за человеком, т. е. от настоящего времени, до Большого взрыва. Члены этого идеального ряда соответствуют в пределах небольшой погрешности фактической хронологии возникновения новых лидеров эволюции. (Откроем школьный учебник биологии и убедимся, что это так!)
Сравним времена, полученные по закону прогрессии и научные данные:
1.69, 5.06, 11.8, 25.3, 52.3, 106, 214, 429, 861, 1724, 3451, 6903, 13810.
1.80, 6.00, 12.0, 25.0, (55–58), 114, 235, 460, 840, 1850, 3500, (8000–10000), 13810.
И вычислим относительные погрешности:
6 %, 16 %, 1.7 %, 1.2 %, 6 %, 7 %, 11 %, 6.5 %, 2.6 %, 4.4 %, 9.2 %, 23 %, 0 %.
Какова вероятность случайного попадания ряда чисел, вычисленных по закону прогрессии, на действительные времена начала эпох с полученными погрешностями? Может быть, один шанс на миллион, а, может быть, и меньше. На самом деле прогрессия эволюции − это уже реальность, а не гипотеза, − странно, что ее до сих пор не заметили.
В статье А.Д. Панова «Эволюция и проблема SETI» отмечено, что продолжительность последовательных фаз эволюции планетарной системы устойчиво сокращается от прошлого к настоящему. Эта последовательность переходов образует геометрическую прогрессию, причем ее знаменатель близок к числу Эйлера е = 2,718.
Если исходить из предлагаемой нами гипотезы, здесь у Панова перемешались две последовательности времен: биосферной эволюции и исторического процесса. Продолжительность периодов биосферной эволюции уменьшается по закону прогрессии эволюции.
Длительность исторических циклов, как интервалов между соседними гармоническими стадиями роста сети человека, в целом также уменьшается по закону, близкому к геометрической прогрессии. Поэтому и выявился закон прогрессии для времен, отмеряющих продолжительность фаз эволюции.
Однако моменты биосферных переходов в работе Панова связываются с какими-то нелепыми фазовыми переходами и катастрофическими событиями в биосфере, которые им соответствуют. Этот катастрофический подход, а главное неспособность автора ввести в рассмотрение отдельную прогрессию для исторического процесса привели к тому, что знаменатель прогрессии оказался завышенным (1/2.7, а не 1/2), и была неверно вычислена «конечная точка эволюции 4х-миллиардолетнего цикла».

