Население Земли как растущая иерархическая сеть

По расчетам Константинова сингулярная точка эволюции приходится на T0 = 2011 ± 4 год, а коэффициент ускорения эволюции z = 2.82 ± 0.05, что, как отмечает Константинов, с учетом статистической погрешности не отличается от результатов, полученных ранее Пановым (T0 = 2015 ± 15–20 лет, z = 2.67 ± 0.15).

По нашим же расчетам, Константинов правильно определив точку сингулярности (2011 ± 4), ошибся в подсчете коэффициента ускорения: его значение для скорректированной последовательности следует взять равным z = 2.73 ± 0.05 (рис. 1), что практически совпадает с оценкой Панова (2.67 ± 0.15).

Рис.1.  Определение коэффициента ускорения z методом наименьших квадратов (Ti – таб. 1, T0 = 2011).

Сведем все данные в таблицу. Для коэффициента ускорения возьмем два значения: 2.82 по расчетам Константинова и 2.73 – по нашим расчетам; отсчет времени ведем от точки сингулярности 2011 год.

Таблица 1. Сравнение последовательности Панова с прогрессией эволюции.

В чем главные отличия последовательности Панова от прогрессии эволюции?

1. Первая – разношерстная: здесь в одном ряду стоят биосферные и геологические катаклизмы, появление новых видов, технологические, исторические, географические, экономические и политические  события. Тогда как вторая – это однородный ряд следующих друг за другом определяющих событий добиологической части универсальной эволюции и, как ее продолжения, биологической эволюции, в котором каждая следующая авангардная система эволюции появляется как прогрессивное усложнение, усовершенствование предыдущей и никак иначе.

2. Последовательность Панова ни в в функциональном, ни в стохастическом смысле не образует прогрессии и потому не может быть проанализирована на предмет неслучайного ее происхождения. Коэффициент ускорения эволюции z = 2.7 равен нецелому (по всей видимости случайному) числу, которое, по мнению Панова, возможно,  совпадает с числом Эйлера (такого же мнения придерживается Коротаев, партнер Панова по коротаевской корпорации). При том, что число это, в отличие от числа π,  как константа никогда не встречается ни в одном законе естествознания. Знаменатель прогрессии эволюции равен двум  с точностью до одного процента, т. е. простейшему целочисленному значению, что также свидетельствует в пользу ее  неслучайного происхождения.

3. Хронология появления новых лидеров эволюции гораздо лучше отвечает закону прогрессии, чем последовательность фазовых переходов биосферы Панова. Это прекрасно отражено в таблице 1, где прогрессия эволюция в логарифмическом масштабе представлена как ряд практически целых чисел от нуля до тринадцати. Чего никак нельзя сказать о последовательности Панова, которую нельзя никаким смещением точки сингулярности и вариацией коэффициента ускорения привести к подобному виду.

4. Последовательность фазовых переходов биосферы Панова сходится к 2015 (± 15–20) году. Что предвещает в начале XXI века для процесса, длившегося четыре миллиарда лет, катастрофу планетарного масштаба. Предел, к которому сжимаются циклы универсальной эволюции, находится в далеком будущем – 1.69 млн лет от настоящего – поэтому никакие глобальные катастрофы в текущем столетии человечеству не грозят.

Каков же итог? Последовательность Панова – не более, чем кривое отражение двух, несводимых к одной прогрессий: прогрессии универсальной эволюции и прогрессии эволюции человека. Отражение скверного качества, поскольку неверно определен коэффициент ускорения. Вертикаль Снукса-Панова-Модиса – конструкция с эвристической точки зрения совершенно никчемушняя, т. к. и до Панова, и до Снукса, и до Модиса было хорошо известно об ускорении эволюции (Поршнев, Дьяконов, Капица…), и эта кривая вертикаль, состоящая из случайно подобранных событий, ничего нового в это знание не привносит.

Но может исказить представление об ускоряющейся универсальной эволюции, которую Панов на языке неравновесной термодинамики описывает как последовательность сжимающихся в режиме с обострением фазовых переходов биосферы с точкой сингулярности в первой половине текущего столетия.

Правило Тициуса-Боде

 Проанализируем прогрессию Тициуса-Боде по той же схеме, что и прогрессию эволюции. Поместим начало отсчета расстояний до планет не в центр Солнца, а на орбиту Меркурия. Затем поделим все эти расстояния на радиус орбиты Меркурия и прологарифмируем результаты по основанию два. Подсчитаем минимальные отклонения логарифмических расстояний от ближайшего целого и построим график зависимости их средних от основания логарифма (рис. 1, 2 ).

 Рис. 1. Средние расстояния планет СС от центра Солнца, от орбиты Меркурия, в масштабе 0.33 а.е. и в логарифмическом масштабе по основанию два, обработанные в системе Mathcad.

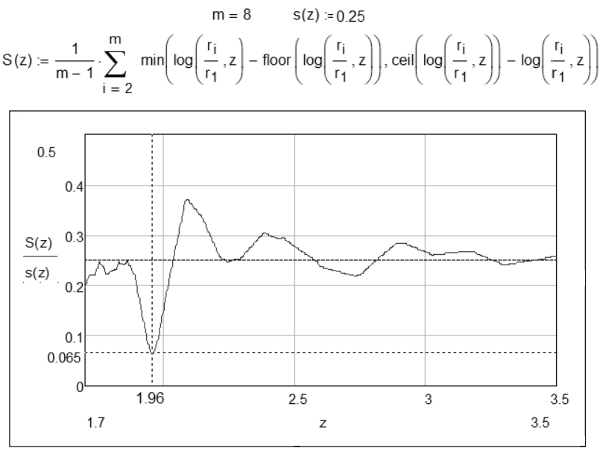
Рис. 2. График зависимости среднего отклонения от ближайших целых чисел логарифмических расстояний планет СС до Меркурия S(z) от основания логарифма z.

Отклонения логарифмических расстояний от последовательности целых чисел лежат в диапазоне [0.1, 0.22], что смотрится не так хорошо, как в случае с прогрессией эволюции. Но их стремление к целочисленности – факт, не подлежащий сомнению. Странным и удивительным кажется совпадение в пределах погрешности знаменателей прогрессии эволюции и прогрессии Тициуса-Боде (рис. 2). (На графике виден отчетливо выраженный минимум при основании 1.96, причем сами средние колеблются в районе 0.25 – средней средних их величины.)

Как образовалась СС и как она сохраняет устойчивость в нынешнем своем состоянии во многом и до сих пор остается тайной за семью печатями. Ясно только то, что влияние планет друг на друга в данный момент ее эволюции крайне мало или даже совсем ничтожно, следовательно, логично считать положение каждой планетной орбиты не зависящим от других. (В этом отличие данного анализа от анализа прогрессии эволюции, для которой такая зависимость существовала: время появление каждого следующего лидера эволюции зависело от времени появления предыдущего.)

События попадания радиусов планет в ε-окрестности целых чисел независимы, следовательно, P = (2×0.224)7 ≈ 4×10-3. Т. к. знаменатель прогрессии Тициуса-Боде, который мог бы быть равен любому действительному числу, оказывается равным двум (2 ± 0.04), то по правилу 2ε это еще на порядок снижает величину данной оценки.

Резонансы периодов массивных быстровращающихся тел Солнечной системы

Существует множество орбитальных и вращательных резонансов, которым подчиняются планеты и спутники СС. Эта тема достаточно подробно разобрана нами в главе «Финальность в устройстве СС». И среди всех этих резонансов выделяется резонанс периодов осевых вращений крупных быстровращающихся планет и астероидов СС, подмеченный астрофизиком Крымской астрофизической обсерватории Валерием Александровичем  Котовым. Выделяется он тем, что в отличие от всех прочих, для него не существует никакого правдоподобного объяснения.

Дело в том, что периоды вращений массивных ротаторов СС не просто соизмеримы  с малой степенью кратности друг по отношению к другу, что характерно для всех прочих резонансов, но имеют также и общую меру, которой все они могут быть измерены. И мера эта, не просто какой-то, ни с чем не связанный отрезок времени, а 160-ти минутный период когерентной космологической осцилляции (ККО). Той самой осцилляции, согласно которой происходят глобальные пульсации Солнечной фотосферы, которой подчиняются временные ряды Солнечных вспышек, по закону которой происходят колебания яркости ядер галактик, вращаются тесные двойные звездные системы.

Таблица 1. Быстровращающиеся планеты Солнечной системы. Отношения периодов обращения планет к периоду Солнца tcc = 160 минут близки к целым числам. Чем больше масса планеты и чем быстрее она вращается, тем ближе отношение к целому числу.

Могут ли подобные, почти целочисленные отношения возникнуть лишь по воле случая? Подсчитаем вероятность такого события по схеме P =  2ε, причем возьмем в расчет только газовые и ледяные гиганты, для которых этот резонанс выражен наиболее выпукло.

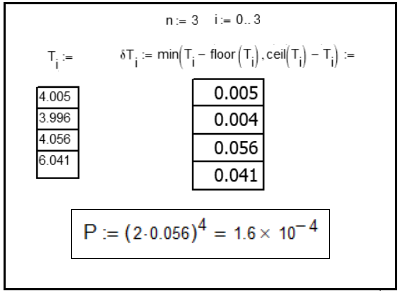
 Рис. 1. Периоды вращения четырех наиболее крупных ротаторов СС и их отклонения от целочисленных значений в единицах tcc = 160 минут.

Можно ли считать резонансность осевых вращений планет СС случайной, ведь все эти резонансы связаны с ККО? Причем связь эта представляется скорее мистической, чем имеющей какое-то рациональное объяснение. Действительно, как в процессе планетогенеза, миллиарды лет тому назад, планеты могли набирать, а затем в результате диссипативных сил сбавлять обороты, да так, чтобы к настоящему времени смогла проявиться столь необычная связь с явлениями, происходящими в недрах звезд и ядрах галактик?

Поскольку все существующие теории формирования СС никакого ответа на этот вопрос не дают, то единственное, что остается, при условии невыхода за рамки современных научных представлений, – считать эти совпадения  независимыми и чисто случайными. Считая периоды вращения планет вокруг своей оси друг от друга не зависящими, получаем: P = (2×0.056)4 = 1.6×10-4[290]. Т. к. в этом расчете не участвуют другие аналогичные резонансы, то очевидно, что P < 10-4.

Разное (от первого лица)

 При работе над сетевой моделью я неоднократно сталкивался с совпадениями, случайное происхождение которых кажется чрезвычайно маловероятным или даже попросту невозможным. О таких невозможных случайностях, вероятность появления которых трудно как-то подсчитать, но тем не менее странных и удивительных, здесь и пойдет речь.

Эта книга никогда не была бы написана, если бы не одно невероятное совпадение. Когда в 2006 году я познакомился с работой С.П. Капицы по гиперболическому росту населения Земли [3], то обратил внимание на следующее обстоятельство: главная константа его теории К = 67000 очень мало отличается от круглого числа 216 = 65536. Это навело меня на мысль попытаться сконструировать биниальную, циклически растущую в соответствии с простым алгоритмом иерархическую сеть, рост которой моделирует рост населения Земли.

После нескольких неудачных попыток мне это удалось, причем оказалось, что если считать время цикла сети постоянным – рост ее будет гиперболическим. Закон простой гиперболы – той самой, которую изучают в школе, и наиболее простой алгоритм самокопирования сети давали один и тот же результат! Возможно, кому-то подобное совпадение не покажется чем то из ряда вон выходящим, но для меня это было сигналом, говорящим о том, что я на правильном пути.

Еще одно совпадение произошло тогда, когда я подсчитал время эволюции человека через возраст Вселенной и прогрессию эволюции: THomo = TUnivers/213 ≈ 1.7 млн лет, и его же – через полное число циклов роста Сети человека и постоянную времени Капицы: THomo = 42399τ ≈ 1.8 млн лет. Поскольку точность, с которой С.П. Капица определил τ, если исходить из диапазона данных им в разное время оценок,  составляет как минимум десять процентов, можно было констатировать практически полное совпадение.

Представление о гармонических стадиях роста Сети человека позволило разбить эволюцию и историю человечества на сжимающиеся по закону прогрессии циклы. И хотя  они не могут быть проанализированы на предмет случайного происхождения по причине трудности достаточно точного определения времен характерных изменений в человеке и социуме, совпадения с данными палеодемографии и мировой истории оказались очень хорошими[291].

Особенно выделяются датировки двух первых после неолита (10000 лет тому назад) гармонических стадий роста Сети человека, которые в точности соответствуют времени появления первых цивилизаций (10000/2 = 5000) и началу осевого времени (10000/4 = 2500). Можно ли считать подобные совпадения всего лишь делом случая?

Главное отличие моей модели от модели Капицы в том, что она позволяет объяснить такие кризисные демографические и социальные явления, как неолитическая революция  и глобальный демографический переход.

В рамках феноменологической теории Капицы можно вычислить время начала неолита (такой же результат следует и из моей модели): Tneol = √Kτ. Но у С.П. Капицы этот поворотный момент эволюции человека и начала истории человеческого социума никак не выделен, тогда как в сетевой модели этот скачок объясняется переходом ко второй, взрывной стадии роста сети, когда впервые за цикл с нуля собирается клаттер.

И это еще одно очень странное совпадение, если считать сетевую модель досужей выдумкой. Действительно, и время начала неолита, и численность в этот момент, и качественные изменения в социуме, вытекающие из моей модели, – полностью соответствуют данным палеодемографии и гиперболе Хорнера.

Теперь о переходе. Теория Капицы объясняет явление мирового демографического перехода исходя из чисто физикалистских соображений, представляя его как системный фазовый переход. С.П. Капица описывает переход как момент «обострения» взаимодействий в демографической системе, за которым с неизбежностью следует качественное изменение законов развития, определяющее его завершение. Ясно, что подобное объяснение «на словах» толком, по сути, ничего не объясняет.

Сетевая же модель, напротив, полностью объясняет этот качественный скачок в эволюции человечества как системы, рассматривая его как операцию репликации сети четвертого ранга, вслед за которой стартует рост сети пятого ранга и эволюция вида, следующего за человеком. И здесь имеется полное совпадение по времени начала и завершения перехода, его продолжительности, численности населения мира в эти моменты времени[292].

К этим странным (если считать сетевую теорию плодом больного воображения) совпадениям следует также добавить феномен удвоения числа носителей сети четвертого ранга на последнем цикле своего роста  (1942 – 1982 гг.), что в точности соответствует данным мировой демографии.

Следующее совпадение связано с Кондратьевским циклом. Его длительность, согласно исследованиям Ю.В. Яковца, по мере подхода к демографической сингулярности приближается к сорока годам, а этот период  в сетевой модели – время цикла Сети человека (фазы роста сети и длинного цикла  мировой экономики тоже в первом приближении совпадают).

Но самое удивительное совпадение произошло тогда, когда я подсчитал время цикла сети пятого ранга и оно оказалось в точности равным периоду когерентной космологической осцилляции. И здесь на самом деле есть чему удивляться. Действительно, получилось t5 = 160,06 ± 0,24 минут; не 159 и не 161, а именно 160, с точностью до четверти минуты. Учитывая то, что времена  t4 (t4 = τКапицы = ТКондр = 40 годам = 40·365 = 14600 суток) и t5  (t5 = tККО = 160 мин = 1/9 суток) подсчитываются по одной и той же формуле, причем первое более чем в сто тысяч раз превосходит второе, такое попадание в яблочко не может рассматриваться как простая случайность.

Есть еще одна особенность моей модели, которая выражается в ряде удивительных совпадений, связанных с числом два. Так, рост населения Земли моделирует биниальная, а не тринитарная или какая-либо другая сеть, рост которой стартует с двух и финиширует в процессе двух циклов двумя же клаттерами. На последнем цикле роста перед переходом (1942 – 1982 гг.) численность населения мира удваивается, за время перехода она также удваивается. Число гармонических стадий роста  Сети человека от совершенной до совершенной равно 24, число периодов эволюции и истории: 24 − 1. Для вида, следующего за человеком, эти значения равны, соответственно, 28  и 28 − 1.

Циклы эволюции человека и исторические циклы, как циклы роста Сети человека, сокращаются по закону прогрессии со знаменателем два (численность населения Земли удваивается с каждым таким циклом). Неолит делит всю историю человечества на два равных в логарифмическом масштабе отрезка времени: эпоху эволюции человека до неолита и исторический период развития человеческого социума после неолита.

Циклы универсальной эволюции сокращаются по закону прогрессии со знаменателем два. Появление первых приматов (и сети ранга нуль) положило начало линии чистого разума (Тейяр де Шарден). Время первых приматов делит весь рабочий цикл универсальной эволюции от Большого взрыва до Большого сжатия на два равных как по времени (измеряемом в логарифмическом масштабе), так и по количеству циклов (8 = 23) эона: зон поиска лидера эволюции и зон его восхождения к Финалу.

И, наконец, есть еще пара, возможно, чисто случайных, но тем не менее странных совпадения, связанных с числом два. Отношение планковской массы к массе нуклона примерно равно круглому числу 264 (числу носителей совершенной сети шестого ранга и числу элементарных составляющих гипотетического существа – планкеона). Отношение числа Эддингтона к постоянной тонкой структуры равно числу носителей финальной совершенной сети универсальной эволюции 2256.

Заключение

Изоморфность модели Капицы и сетевой модели

Синергетическая модель гиперболического роста населения мира С.П. Капицы и наша телеологическая сетевая модель с постдетерминацией, как мы это здесь покажем, есть, по сути, две изоморфные модели сложного многофакторного процесса: гиперболического роста населения Земли. Но сначала разберемся с терминологией.

Термин модель, а не теория или гипотеза, возможно, лучше подходит при определении абстрактной умозрительной схемы, предложенной С.П. Капицей для объяснения феномена гиперболического роста населения Земли. То же самое можно сказать и о нашей работе. В обоих случаях мы имеем мысленно созданную структуру, которая воспроизводит часть действительности в схематизированной, идеализированной, упрощенной и наглядной форме.

Обе модели представляют собой элемент научной картины мира, который содержит компонент фантазии, творческого воображения. Обе они по отношению к реальному процессу роста населения Земли – процессу высшей степени сложности – являются гомоморфными, а по отношению друг к другу, как мы это сейчас покажем, – изоморфными.

Изоморфизм и гомоморфизм (греч. isos – одинаковый, homoios – подобный и morphe – форма) – понятия, характеризующие соответствие между структурами объектов. Две системы, рассматриваемые отвлеченно от природы составляющих их элементов, являются изоморфными друг другу, если каждому элементу первой системы соответствует один и только один элемент второй системы, а каждой связи в одной системе соответствует аналогичная связь в другой и наоборот.

Такое взаимно-однозначное соответствие называется изоморфизмом. Гомоморфизм отличается от изоморфизма тем, что соответствие объектов (систем) однозначно лишь в одну сторону, и тождество между объектом и моделью выполняется лишь в заданном интервале абстракции. Поэтому гомоморфный образ есть неполное, приближенное отображение структуры оригинала. (Таково, например, отношение между картой и местностью.)

Следует иметь в виду, что отношение гомоморфизма между природным явлением и натурфилософской теорией, которой оно описывается, определяет лишь логический образ этого явления, а это совсем не одно и то же, что само явление, в каком бы приближении его не рассматривать. Так, логика автора математической теории роста населения Земли, происходящая из его головы, не тождественна и не подобна последовательности причинно-связанных социально-демографических процессов, происходивших в пространстве и во времени и генерировавших гиперболический рост. Логика, присущая мышлению человека, – не есть зеркало каузальности природных явлений.

Если же говорить об изоморфизме двух мысленно созданных динамических моделей роста населения Земли, то, во-первых, они должны быть структурно подобны друг другу, и, во-вторых, должно быть выполнено взаимно-однозначное соответствие между качественными и количественными закономерностями процессов, являющихся в этих моделях логическими образами процессов объекта-оригинала. Изоморфный означает имеющий аналогичную форму. Поэтому, когда говорят, что одна модель изоморфна другой, то имеют в виду, что, по крайней мере, чисто формально они эквивалентны и взаимозаменяемы.

Рассмотрим элементы, связи, а также свойства и закономерности, описывающие динамический процесс роста населения мира в модели Капицы и в сетевой модели и установим между ними взаимно-однозначное соответствие. Начнем с целочисленной переменной – численности населения Земли, которая является главным показателем моделируемого динамического процесса. Эта переменная присутствует в обеих моделях. Разница в том, что во второй модели численности народонаселения в каждый момент времени сопоставляется сумма узлов или носителей растущей иерархической сети.

Совокупность элементов, будь то численность населения мира или число узлов сети, рассматривается в обоих случаях как единая, согласованно растущая во всех своих частях и синхронно развивающаяся система. И, если в первой модели согласованность и синхронистичность роста хотя и признается, но остается необъясненной, то во второй – эти свойства напрямую вытекают из алгоритма роста сети.

Обе модели описывают рост численности населения мира на последовательности циклов (периодов) эволюции и истории, сокращающихся по закону прогрессии к точке сингулярности эмпирической гиперболы демографического роста. Причем эта численность за каждый такой цикл возрастает во столько же раз, во сколько этот цикл сокращается по сравнению с предыдущим.

В модели Капицы таких циклов 11, в сетевой модели – 15. Феномен начала роста, неолитическая революция, константы Капицы, три самые важные даты в истории человечества, принцип демографического императива (принцип эквифинальности роста и развития), глобальный демографический переход, проблема устойчивости роста – все эти понятия, проблемы и явления обозначены в обеих моделях. Причем между элементами, связями и закономерностями в модели Капицы и в сетевой модели может быть установлено взаимно однозначное соответствие:

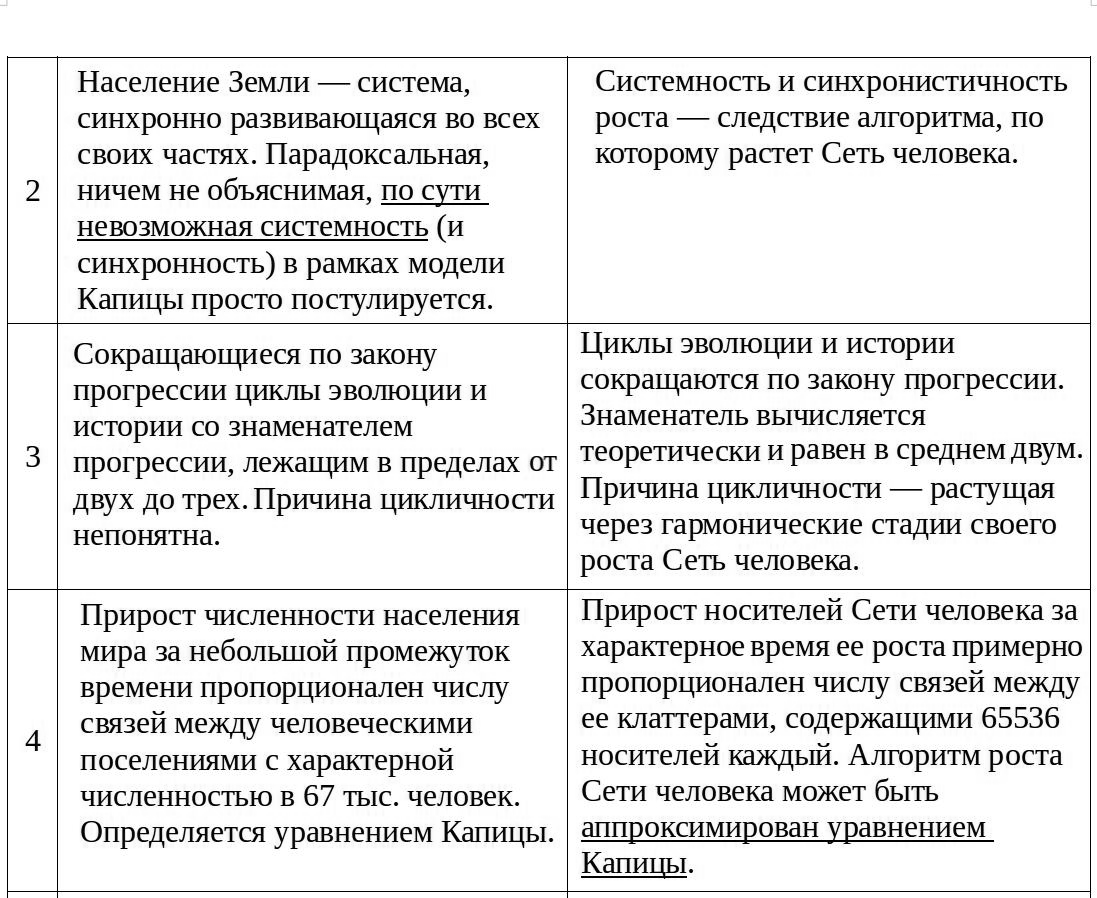
Таблица 1. Взаимно однозначное соответствие между элементами, связями и закономерностями в модели Капицы и в сетевой модели.

Т. к. между элементами, связями и закономерностями первой и второй модели установлено взаимно однозначное соответствие – можно считать их изоморфными. Следует отметить, что полный изоморфизм возможен лишь для чисто математических моделей и недостижим для феноменологических, описательных моделей.

* * *

В чем же отличие между моделью Капицы и сетевой моделью? Отличие в том, что первая выстроена так, чтобы при полном отсутствии необходимой математики, т. е. чисто на словах, полностью отвечать синергетическому, бессмысленному для данной проблемы клише с соответствующей терминологией, как то: автомодельный рост, масштабная инвариантность, самоподобное социальное развитие, нелинейные связи, динамический хаос, режим с обострением, фазовый переход…