Население Земли как растущая иерархическая сеть

Первый и второй эон – это время поиска лидера эволюции, способного начать процесс интеграции сетей. Старт эволюции идет от бариона; «материальные» носители первого эона эволюции это: ядра, атомы, молекулы, клетки. В его финале эволюция из микромира переходит в макромир. В течение второго эона разнообразие видов направленной биологической эволюции в последовательности «мутовка – веер – мутовка» уменьшается от Кембрийского взрыва до появления первых приматов.

И вот, наконец, найден лидер эволюции первых двух эонов. Им стали популяции первых приматов и сети нулевого ранга, их сопровождающие. Уровень носителя с клеточного поднимается на «организменный». Третий и четвертый эон – это время роста, конкуренции (проигравшие, как правило, выбывают) и экспансии этих сетей. Прогрессивные изменения сети и носителя происходят скачками при достижении сопровождающей сетью гармонической и (особенно) совершенной стадии. Число носителей совершенной сети каждого следующего этапа эволюции равно квадрату предыдущего.

* * *

Рассмотрим относительные погрешности, с которыми прогрессия эволюции определяет начало каждой эпохи:

6 %, 16 %, 1.7 %, 1.2 %, 6 %, 7 %, 11 %, 6.5 %, 2.6 %, 4.4 %, 9.2 %, 23 %, 0 %.

Какова вероятность случайного попадания ряда чисел, вычисленных по закону прогрессии, на действительные времена начала эпох с полученными погрешностями? Может быть, один шанс на миллион, а может быть, и меньше[92]. На самом деле прогрессия эволюции – это уже реальность, а не гипотеза.

В статье А.Д. Панова: «Эволюция и проблема SETI» отмечено, что продолжительность последовательных фаз эволюции планетарной системы устойчиво сокращается от прошлого к настоящему. [9] Эта последовательность, по его мнению, образует геометрическую прогрессию, знаменатель которой примерно равен основанию натуральных логарифмов.

Ошибка Панова в том, что он объединяет в одну прогрессию две разнородные последовательности времен: даты биосферных революций и вехи исторического прогресса. Действительно, продолжительность периодов биосферной эволюции уменьшается по закону прогрессии эволюции. Длительность периодов эволюции человека и исторических циклов, как интервалов между соседними гармоническими стадиями роста Сети человека, в целом также уменьшается по закону, близкому к геометрической прогрессии. (При этом у них в первом приближении один и тот же знаменатель.)

Но предположение о том, что эти две последовательности принадлежат одной прогрессии, которое Панов неявно постулирует, является ошибочным. Что приводит его к абсурдному выводу о биосферном кризисе с 4-х миллиардолетней (!) историей накопления противоречий в первой половине XXI века.

* * *

В связи с существованием прогрессии эволюции возможен иной, «сетевой» взгляд на эволюцию:

Каждая эпоха, отмеченная в таблице, связана со своей авангардной системой эволюции. Сети, её сопровождающие, выполняют план своего роста в соответствии с заложенным в них алгоритмом. Рост каждой сети и эволюция материального авангарда, с ней связанного, находятся в причинно-следственной зависимости: сеть – причина.

Совершенная стадия роста сети определяет конец эволюции текущего авангарда, а начало роста сети более высокого ранга соответствует началу эволюции следующего. Внутри эпохи наиболее значимые изменения авангардной системы эволюции приходятся на моменты прохождения сетью гармонических стадий своего роста.

* * *

Разбиение времени эволюции на тринадцать периодов от Большого взрыва до наших дней, разбиение исторического времени на восемь циклов исторического развития и разбиение планетарной зоны Солнечной системы по правилу Тициуса–Боде на восемь зон – выполнено по одному и тому же закону: по закону геометрической прогрессии со знаменателем ½.

Причем это никакая не нумерология, а факты, которые нужно как-то объяснять. Если здесь не поработали силы, природа и происхождение которых нам неизвестны, то остается единственная возможность: объяснить все это естественными причинами. Но кто возьмется найти такое объяснение?

Константы Капицы

Постоянная Фёрстера и возраст Вселенной

Первая из фундаментальных констант, характеризующих развитие человечества как системы – это постоянная Фёрстера. Как она была получена? Имея большой объем данных по численности населения Земли от Р.Х. до 1960 года, немецкий инженер австрийского происхождения Хейнц фон Фёрстер вместе с П. Moрa и Л. Амиот подыскивал простую аналитическую зависимость, которая могла бы послужить неплохим приближением для имеющихся у него демографических данных.

Прежде всего, он, вероятно, предположил, что численность популяции Homo sapiens, как и численность всякой другой популяции в условиях избытка ресурсов, росла экспоненциально. По этому простому закону, когда при удвоении численности удваивается и естественный прирост, растет все живое. Зависимость логарифма численности от времени должна быть в таком случае линейной.

Когда он нанес данные на координатную плоскость, его ожидал сюрприз: график аппроксимирующей зависимости не укладывался на прямую, рост логарифма численности от времени по непонятной причине оказался круче линейного, и гипотезу экспоненциального роста пришлось отбросить.

Это был довольно неожиданный результат, хотя, возможно, и не слишком, ведь если вдуматься рост численности человечества, как системы высшей степени сложности, подверженной кризисам, войнам и эпидемиям, вряд ли должен подчиняться экспоненциальному закону.

На самом деле предположение о том, что численность населения Земли могла расти экспоненциально не заслуживает никакого доверия. Действительно, рост мог бы быть экспоненциальным, если бы человечество можно было считать популяцией, т. е. если бы оно было однородной массой с единым для всех ее частей естественным приростом. Однако в действительности – это конгломерат, образованный различными как по численности, так и по естественному приросту популяциями. (Коэффициент естественного прироста в разные времена, для разных народов мог различаться в разы, поэтому никакое его усреднение по всей массе человечества не может считаться приемлемым.) Даже если допустить, что численность каждого народа, этноса может расти экспоненциально – из этого вовсе не следует, что численность человечества также будет расти экспоненциально.

Если руководствоваться здравым смыслом, то вообще трудно себе представить, что этот рост может быть описан с помощью какой-то простой формулы. Априори представляется, что здесь должна быть справедлива гипотеза близкая к нулевой.

Известно, что рост происходил без спадов (возможно, за редкими исключениями) и скорость роста тоже почти всегда росла – по крайней мере в среднем. Тогда зависимость численности от времени можно в первом приближении считать монотонно возрастающей функцией.

Но какой-то простой формулы, описывающей эту зависимость, – не существует. Такой рост может быть представлен как суммарный рост слабо связанных подсистем: этносов, стран или народов и нет никакого смысла искать глобальный закон роста справедливый для всего населения планеты, действовавший на протяжении двадцати веков.

Для каждого этапа такого, вообще говоря, случайного роста, для всех его взлетов и падений, – историки, социологи и демографы нашли бы, конечно, какое-нибудь естественное объяснение и всякая математика была бы здесь бесполезна.

Возможно, так же полагал и Фёрстер, потерпев неудачу с гипотезой экспоненциального роста. Каким должен быть следующий его шаг, что мог бы предпринять любой другой исследователь, попавший в подобное положение? Можно было бы попытаться подобрать полином, хорошо аппроксимирующий демографические данные, но такой полином, достаточно высокой степени, всегда можно найти и в этом нет никакого достижения… Можно попробовать в качестве кандидата степенную функцию N = C/(t0 – t)p, ведь проще нее, кажется, вообще ничего нет. Что, собственно, и было сделано.

К закону степенного роста Фёрстера и его коллег привело фантастическое предположение о том, что коэффициент мирового естественного прироста на всем протяжении исторического процесса не был постоянен, как при экспоненциальном росте, а слабо зависел от численности: a = a0N1/k. (Такая зависимость могла бы, по их мнению, существовать, если в соответствии с теорией игр рассматривать растущее население Земли как некую коалицию, ведущую глобальную игру против сил природы.)

Важно понимать, что это предположение, сделанное благодаря модной в то время теории игр (спасибо ей за это!), расходящееся со здравым смыслом и требующее большой вычислительной работы, – представляется совершенно фантастическим, если не безумным. Результат точно должен был получиться отрицательным, т. е. точность значений С, p и t0 должна была оказаться очень небольшой.

Но совершилось чудо – эта точность, с которой определились постоянные Фёрстера, совершенно неожиданно оказалась чрезвычайно высокой, можно даже сказать невозможно высокой, делающей гиперболу Фёрстера, по сути, предзаданной:

Результаты исследования Фёрстера и его коллег данных по численности населения Земли за последние две тысячи лет методом наименьших квадратов: N = C/(t0 – t)p; C = 179 ± 14 млрд; t0 = 2027 ± 5; p = 0,99 ± 0,009.

Здесь важно то, что показатель степенной функции, описывающей рост, оказался практически равным единице, т. е. простейшему целочисленному значению. (При вычислении p по методу наименьших квадратов могло быть получено любое действительное число, например, p = 0,78 или p = 1,16, но вышло, что p = 1 с точностью до одного процента.)

Вряд ли целочисленность p является всего лишь делом случая. Такое совпадение возможно, но, очевидно, весьма маловероятно. Скорее всего, за этим стоит нечто большее, позволяющее считать население мира единой системой. И по причине этой «невозможно» высокой точности для p и t0 только и можно говорить о новой фундаментальной константе С, Фёрстера, характеризующей растущее человечество как систему. Стоит отметить, что сам Фёрстер, хотя и шутил на эту тему, но так и не понял ни причины, ни значения открытого им аномального гиперболического роста.

Немецкий физик Себастьян фон Хорнер[93] расширил время действия закона Фёрстера до неолита, подключив дополнительные данные, что несколько увеличило постоянную Фёрстера С и оставило практически без изменения p и t0 [1]:

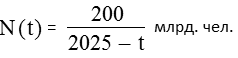
Рис. 1. Гипербола Хорнера.

Итак, в начале шестидесятых годов прошлого века была введена новая, видимо, фундаментальная постоянная, определяющая рост численности Homo sapiens и его эволюцию, смысл которой для ее первооткрывателя так и остался непонятым. Размерность этой эмпирической константы, как следует из формулы Фёрстера, – год в степени 0,99. Что позволяет предположить, что p = 1 и постоянная Фёрстера имеет размерность времени. Однако авторы статьи «Судный день. Пятница 13 ноября 2026 года» гипотезу о целочисленности p не рассматривали, что, кстати, не позволило им определить постоянную С с максимально возможной точностью.

Действительно, значение C = 179 ± 14 млрд лет было получено в предположении о том, что показатель p является неопределенным и должен вычисляться по методу наименьших квадратов так же, как C и t0. Что представляется вполне логичным. Но получив для него столь близкое к единице значение, Фёрстер и его коллеги должны были сделать перерасчет на основе тех же самых данных, полагая, что p = 1.

Этого сделано не было, и значение постоянной Фёрстера оказалось несколько заниженным. Далее мы приведем наши расчеты, которые позволяют уточнить значение постоянной С, приведенное в статье «Судный день. Пятница 13 ноября 2026 года». Эти расчеты хотя и не могут считаться вполне корректными, зато дают возможность определить постоянную С при p = 1 на основе результатов, полученных Фёрстером и его коллегами: C = 188 ± 14 млрд лет. (Данные, использованные ими, опубликованы не были.)

* * *

Теперь мы вплотную подошли к вопросу о смысле постоянной Фёрстера. Что означают эти 188 миллиардов лет? – Непонятно… но уж только не численность народонаселения за год до сингулярности, т. к. до этого значения она точно не дорастет. Есть один интервал времени, известный из космологии, который по порядку величины близок к данной константе: это возраст Вселенной TUniverse = 13,8 млрд лет. Если постоянная Фёрстера С имеет космологический смысл и как-то связана с универсальной эволюцией, то ее отношение к возрасту Вселенной F = C/TUniverse, не имеющее размерности, должно вытекать из некой финалистской теории эволюции.

Согласно нашей теории С = kK2τ, возраст Вселенной TUniverse ≈ TSingularity = 213N4τ = 213N4C/kK2 (K = 65536, k = 1,1 – зомби-коэффициент, N4 = 42399 – полное число циклов сети человека, TSingularity – интервал времени от Большого взрыва до недостижимой космологической сингулярности), следовательно F = C/TUniverse ≈ C/TSingularity = kK2/(213N4) = 13,6 (доверительный интервал обозначить затруднительно из-за неопределенности в значении зомби-коэффициента). Что полностью соответствует астрофизическим и демографическим данным: F = (188 ± 14)[94]/13,8 = 13,6 ± 1.

Таким образом, теория роста сети четвертого ранга позволяет вычислить возраст Вселенной с помощью постоянной Фёрстера: TUniverse = C/F =13,8 ± 1 млрд лет. Однако высокой точности ожидать здесь не следует: дело в том, что точность, с которой может быть определена постоянная C ограничена по принципиальным соображениям.

Если принять, что С = 191 ± 4 млрд, что представляется, по нашему мнению, наиболее правдоподобным (см. далее), то эта точность значительно возрастает: TUniverse = 14,0 ± 0,3 млрд лет. Теория роста сети пятого ранга, как мы это покажем в дальнейшем, позволяет вычислить возраст Вселенной с точностью до пяти значащих цифр: TUniverse = 13,8050 ± 0,0002 млрд лет.

* * *

С другой стороны, зная возраст Вселенной можно найти постоянную Фёрстера: C = FTUniverse = 188 млрд лет, и гипербола роста населения Земли может быть определена с точностью до «начального» условия. (Важным отличием нашей модели от всех прочих является то, что постоянную Фёрстера можно вывести из космологических данных.) В качестве «начального» условия выберем значение численности в тот момент времени tc, когда сеть становится совершенной: N(tc) = k·K2 = 1,1·232 = 4,72 млрд; в этот момент, согласно теории, до сингулярности остается всего лишь шаг исторического времени.

По демографическим данным, довольно точным для второй половины XX столетия, находим, что tc = 1982 г. Теперь можно найти точку сингулярности теоретической гиперболы: t0 = 1982 +188 /4,72 = 2022 г. Поскольку гиперболическое уравнение N = C/(t0 – t), постоянная Фёрстера C и точка сингулярности t0 были выведены на основе теории роста сети четвертого ранга – эмпирический закон гиперболического роста населения Земли, открытый Фёрстером, получен нами теоретически.

Отметим разницу между теориями, объясняющими гиперболический рост населения мира на основе нелинейного дифференциального закона (уравнения), связывающего мировой естественный прирост с текущей численностью (dN/dt = N2/C), и нашей финалистской теорией. Пропорциональность прироста численности ее квадрату в таких редукционистских теориях объясняется чисто умозрительно (на самом деле постулируется), а коэффициент пропорциональности 1/С – берется из работы Фёрстера. Гипербола мирового демографического роста получается здесь как решение этого дифференциального уравнения.

Наша модель построена иначе. Она не основана на законе квадратичного роста как на причинном дифференциальном законе, описывающем автокаталитический процесс. Постоянная C = 188 млрд лет, точка сингулярности t0 = 2022 г. и закон гиперболического роста N = C/(t0 – t) выводятся нами чисто теоретически из алгоритма роста сети четвертого ранга и космологических данных без всякой опоры на дифференциальный закон и результаты работы Фёрстера и его коллег[95].

Расщепление постоянной Фёрстера С на константы

Капицы К и τ

Сравним сначала законы экспоненциального и гиперболического роста численности популяции с точки зрения возможности введения в рамках этих законов характерных масштабов времени и численности.

Рис. 1. Экспоненциальный и гиперболический закон роста численности популяции.

Если математические уравнения, описывающие некий закон, не содержат масштаб, в котором могут быть измерены входящие в него переменные, то такой закон называется масштабно-инвариантным относительно этих переменных. В физике масштабная инвариантность означает неизменность уравнений, описывающих какой-либо процесс при изменении всех расстояний и промежутков времени в некоторое число раз. В теории фракталов под масштабной инвариантностью, самоподобием понимают неизменность структуры фрактала при изменении масштаба протяженности, в котором он наблюдается.

Насколько правомерно говорить о масштабной инвариантности закона роста населения Земли, как это делает С.П. Капица, основываясь лишь на том факте, что рост этот описывается степенным законом?

Возникает вопрос: масштабная инвариантность чего? Масштабная инвариантность – это неизменность уравнения или структуры. Речь здесь явно не может идти ни о какой структуре исторического или демографического процесса во времени. Никто же не станет всерьез утверждать, что каждый из исторических циклов в модели Капицы – это сжатая копия предыдущего!

Остается степенная зависимость численности от времени, которая, как и всякая другая степенная зависимость, является инвариантной к масштабам, в которых измеряются входящие в нее переменные. (Т. е. степенная зависимость N(t) сохраняется при изменении масштабов N и t.) Что позволяет в этом смысле говорить о законе роста населения мира, как о законе масштабно-инвариантном.

Но несет ли такая масштабная инвариантность этого закона какой-либо смысл, объясняется ли эта его чисто математическая инвариантность природой процесса роста численности населения Земли или не имеет к ней никакого отношения? Ведь даже в каузальном отношении суть его остается непонятной.

В случае экспоненциального роста показатель n = 1, дифференциальный закон роста является линейным и экспоненциальная зависимость численности от времени содержит встроенный в этот закон масштаб времени τ = 1/α. Что это означает?

Это означает то, что такой рост и такой закон роста нельзя считать масштабно-инвариантными по отношению к переменной t. Действительно, за время τ численность популяции всегда возрастает в 2,7 раза независимо от того, какого значения она достигла к этому моменту времени.

Это свойство закона экспоненциального роста популяции уникально по сравнению со всеми другими законами роста, вне зависимости от того является ли этот закон причинным или таковым не является, т. е. определяет ли положительную обратную связь между численностью и естественным приростом или не определяет, а выражает лишь связь чисто функциональную, непричинную (не ПОС), сопутствующую.

Причина уникальности – в линейности дифференциального уравнения, описывающего рост, и как следствие этой линейности, – независимости (в случае линейной ПОС между численностью и приростом) роста каждой части популяции от другой.

* * *

Следует отметить, что никакого встроенного масштаба численности закон экспоненциального роста популяции не содержит, т. к. численность за время τ возрастает, как мы уже отмечали ранее, в 2,7 раза независимо от того, с какого значения начался ее рост.

Закон гиперболического роста (n > 1), так же как и любой другой степенной закон, является в указанном нами смысле масштабно-инвариантным и не содержит никаких «встроенных» в этот закон масштабов времени и численности.

Например, если N(t) = Ctm и взять t1 = kt, а N1 = kmN, то закон роста останется неизменным: N1 = Ct1m, т. е. он оказывается инвариантным по отношению к согласованному изменению единиц измерения времени и численности (увеличению первой в k раз, второй – в km раз).

Чего не скажешь о законе экспоненциального роста; если N(t) = Noet/τ и взять, например, t1 = kt, то никаким изменением масштаба N1 = k1N закон роста к прежнему виду не привести: N1(t) = No(et/τ)k → N1(t) = No1-k(N(t))k ≠ k1N(t).

* * *

Если сравнивать законы экспоненциального и гиперболического роста популяции с точки зрения характерных масштабов времени и численности, то необходимо отметить, что независимо от их каузальной интерпретации, закон экспоненциального роста содержит «встроенный» в этот закон масштаб времени, но не содержит никакого «встроенного» в него масштаба численности.

Закон же гиперболического роста, как таковой, не содержит никаких «встроенных» в этот закон масштабов времени и численности. Но если для него существует некий «сторонний», не связанный с уравнением роста масштаб, например, масштаб времени τ, то масштаб численности определяется с полной однозначностью из условия N1 = C/τ (n = 2).

Действительно, если поделить числитель и знаменатель выражения N(t) = C/(t0 – t) на характерное время τ (в общем случае делим на τn-1), то время роста будет выражаться в единицах характерного времени τ, а численность в характерных единицах численности: N' = C/τ. Т. е. закон гиперболического роста популяции, в отличие от закона экспоненциального роста, либо вообще не имеет никаких характерных масштабов ни для N, ни для t, либо имеет их сразу оба.

Есть еще одно важное отличие экспоненциального роста популяции от гиперболического. Заключается оно в том, что эволюция популяции, численность которой растет по экспоненциальному закону, не может происходить циклически, тогда как в случае гиперболического роста с характерным временем и характерной численностью ее эволюция, по-видимому, должна быть циклической.

Что означает понятие цикличность в применении его к процессу роста популяции? Цикличность – это ритм, в котором происходит ее эволюция; ритм, связанный с процессом роста и с четко обозначенными на шкале абсолютного времени фазами этого процесса, отмечающими его подъем, стабилизацию и стагнацию.

Если считать численность растущей популяции мерой ее эволюции, то ее экспоненциальный рост (независимо от его каузальной интерпретации) не может быть связан (причинно или функционально) с каким-либо циклическим эволюционным процессом. Дело в том, что рост популяции будет здесь процессом однородным во времени и цикл ее эволюции может иметь любой период и любую фазу. Что не позволяет зародиться никакому циклу, связанному с растущей численностью.

Что же касается гиперболического роста, то, во-первых, этот рост в силу своей нелинейности, выражаемой простейшим аналитическим законом, подразумевает системность растущей популяции[96], т. е. связность всех ее частей, поэтому общая численность популяции может служить здесь мерой, характеризующей ее эволюцию. И, во-вторых, рост этот по определению имеет одну особенность: точку на оси времени, в которой эта численность устремляется к бесконечности.

Циклы роста и развития могут быть введены здесь обратным отсчетом времени от точки сингулярности в прошлое с периодом, равным характерному времени. (Такое определение цикличности эволюции и развития в процессе гиперболического роста является, разумеется, чисто формальным. Подробнее см. главу «Законы роста численности изолированных популяций».)

Если связь между скоростью роста и численностью населения мира не является причинно-следственной, а является всего лишь сопутствующей, то должен существовать некий причинный закон (возможно, с постдетерминацией), который обеспечивает такой не автокаталитический рост. Кроме того, этот же причинный закон будет определять характерное время и характерную численность, которые являются по отношении к закону гиперболического роста населения мира в таком случае сторонними.

И, что особенно важно, так это то, что эти сторонние масштабы времени и численности должны быть характерными масштабами на всех этапах такого роста: в том числе на начальном его этапе, а также во время перехода. Поэтому, в случае роста населения Земли, значения этих констант, полученные для начала демографического перехода, могут быть использованы и при описании гиперболического роста.

* * *

Постоянную Фёрстера С = 187 млрд лет, имеющую размерность времени, можно представить в виде произведения постоянных роста тремя различными способами:

1. Исходя из нашей модели.

2. Исходя из модели Капицы.

3. Чисто эмпирически: используя значение численности на момент завершения эпохи гиперболического роста и начала демографического перехода.