 Полная версия
Полная версияНаселение Земли как растущая иерархическая сеть
8. В 1982 году численность носителей сети, согласно нашей теории, достигла круглого значения 232 человек. Из этого следует, что эпохи перемен наступали не просто тогда, когда эта численность удваивалась по сравнению с предыдущим периодом, а когда становилась равной 2n – двойке в некоторой целой степени. И здесь нет никакой нумерологии – это просто факт, который нужно как-то объяснять.
9. Для полноты картины можно добавить также и «ненаучный» аргумент в подтверждение уникальности, неповторимости и значимости того краткого момента истории конца семидесятых начала восьмидесятых годов прошлого столетия, о котором идет речь. Ведь именно на это время приходится пик активности НЛО, активности невиданной за всю историю наблюдений этого явления. Нечто подобное было зафиксировано еще только один раз спустя десятилетие в 1990 году.
Ответа на вопрос, что же в действительности произошло в конце семидесятых, начале восьмидесятых годов двадцатого века, в чем причина цикличности развития и гиперболического роста населения Земли применяемая здесь феноменологическая схема не дает. Но можно считать, как было показано нами ранее, что именно в это время (в 1982-м, а не в 1965 году) закончился рост человечества по закону гиперболы и начался глобальный демографический переход. И тогда же завершился последний, восьмой исторический период, а вместе с ним и циклический ход мирового исторического процесса.
Существует ли теоретическая формула зависимости численности населения Земли от времени?
Казалось бы, не может быть никакой теоретической формулы, описывающей гиперболический рост численности населения мира. А постоянная Фёрстера и точка сингулярности гиперболы демографического роста – чисто эмпирические константы.
Тем не менее, если квант исторического времени существует, алгоритм восьми шагов отвечает действительности, а в момент окончания гиперболического роста численность носителей сети достигает значения 232 – такую формулу легко сконструировать:
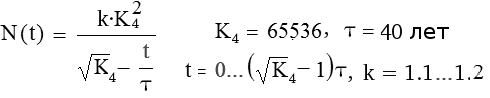
Рис. 1. Теоретическая зависимость численности населения Земли от времени N(t). Отсчет времени ведется от начала неолита; K4 ≈ K; K, τ – постоянные Капицы; k – зомби-коэффициент, учитывающий долю народонаселения, находящуюся вне Сети.
Длительность исторического цикла τ положим равной сорока годам, отсчет времени ведем от начала неолита. Гиперболический рост занимает 255 циклов; в момент его окончания в 1982 году численность носителей сети достигает значения 232, а численность населения Земли, соответственно, k·232 = 4.7 млрд и данная формула перестает правильно описывать рост.
Сингулярность теоретической гиперболы, сингулярность Дьяконова – Капицы, наступает в момент времени t = 256τ. Постоянная K4, определяющая рост, связана с безразмерной константой Капицы К и с постоянной Фёрстера С следующим образом: K = √k· K4 = 1.05·65536 = 68700, С = k·K42τ = 1.1·655362·40 = 1.89·1011 лет.
* * *Здесь нужно отметить следующее: если алгоритм восьми шагов отвечает действительности, то постоянная K4 в формуле на рис. 1 (приблизительно равная постоянной Капицы К) должна быть в точности равна 65536. Действительно, в соответствии с теорией Капицы, а также согласно нашей теории, произведение корня квадратного из K4 (K) на τ равно продолжительности всего исторического периода развития человека, как его обычно принято определять: от неолита до наших дней. Следовательно, корень из K4 (K) равен числу циклов до сингулярности Дьяконова – Капицы, т. е. 256, а K ≈ K4 = 2562 = 65536. Показатель сжатия исторических периодов в таком случае должен быть равен двум, а не 2.7, как в работах С.П. Капицы.
С.П. Капица в последней своей работе «Парадоксы роста…» 2010 года «пришел все таки к выводу», что показатель сжатия исторических периодов должен быть равен двум (стр. 182). Т. к. за момент начала неолита у него взята дата 9000 лет до н. э., т. е. мало отличается от той, что принята в нашей модели, то не только количество циклов, которых должно быть 15, а не 11, но и разметка исторического времени на эти циклы у него должна быть примерно такой же, как у нас[55].
Постоянная τ, единственная размерная постоянная, определяющая гиперболический рост, есть не что иное как: постоянная времени Капицы, время цикла растущей сети в нашей модели, длительность Кондратьевского цикла, продолжительность последнего, восьмого исторического периода 1942–1982 гг., половина длительности глобального демографического перехода 1982–2062 гг. Это фундаментальная постоянная времени, задающая масштаб, в котором должно измеряться историческое время от неолита до наших дней.
Зависимость численности населения Земли от времени в соответствии с предложенной формулой на рис. 1, так же как показатели продвижения цивилизации по пути исторического развития от начала неолита до 1982 года, зависели только от отношения времени t к постоянной τ, т. е. от количества циклов, пройденных Мир-системой к моменту времени t.
* * *Если отсчет времени вести в циклах от сингулярности Дьяконова – Капицы в прошлое, теоретическая гипербола приобретает наиболее простой вид:

Рис. 2. Зависимость численности населения Земли от числа циклов до исторической сингулярности N(T).
Например, чтобы подсчитать сколько людей проживало в 1700 году сначала находим число циклов до сингулярности Дьяконова – Капицы: (2022–1700)/40 = 8,05 цикла. Затем 1,14·4,3 миллиарда делим на 8,05 и получаем 610 миллионов человек.
* * *Средняя длительность инновационных циклов, так же как продолжительность глобальных исторических периодов Мир-системы, выражается через фундаментальную константу исторического времени τ по одной и той же формуле (обобщение гипотезы Й. Шумпетера):
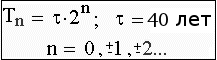
Рис. 3. Длительность экономических и глобальных исторических циклов, выраженная через квант исторического времени τ.
При этом продолжительность сокращающихся по закону прогрессии исторических циклов Дьяконова – Капицы может быть получена, если брать целые неотрицательные значения n в пределах от нуля до семи. Если же брать значения n > 7, то получаются периоды эволюции Homo sapiens, но расположение этих периодов на оси времени не отвечает данным палеоантропологии, т. е. применяемая феноменологическая схема перестает соответствовать действительности.
Отрицательные значения параметра n = -1, -2, -4 в формуле (7) задают среднюю длительность экономических циклов Кузнеца, Жугляра и Китчена. Любопытно, что при n = -9, -11, -14 получаем, причем с приличной точностью, для продолжительности коротких инновационных циклов: месяц, неделю и сутки соответственно. Все это говорит о финальности, предопределенной цикличности мирового исторического процесса.
В заключительной главе книги Виктора Феллера «Предположение о структуре истории» рассмотрена схема построения исторических циклов, «атомом» в которой являются» одни сутки исторического времени. Возможно, это случайное совпадение, но нельзя не отметить, что продолжительность инновационных циклов и циклов Дьяконова – Капицы может быть получена простым умножением времени обращения Земли вокруг своей оси в наше время (с момента своего возникновения 4.5 млрд лет назад из-за приливных сил Земля постепенно замедляла свое вращение) на двойку в некоторой целой степени.
* * *Теоретическая гипербола на рис. 1 наилучшим образом описывает рост численности населения мира от неолита до 1982 года, т. к. лучше всего соответствует работе Фёрстера, исследованиям С.П. Капицы, работе Мак-Эведи, Джоунса и Кремера, данным Остина и Брауэра. Это действительно так, поскольку, во-первых, постоянная Фёрстера, вычисленная по формуле С = k·K42τ = 1.89·1011 (k = 1.1) равна усредненному ее значению по всем этим работам (см. главу «Константы Капицы»). И, во-вторых, точки сингулярности (256·39.75 = 8154 +2022 = 10176) – также совпадают.
Почему формула на рис. 1 столь хорошо описывает рост населения Земли, какой циклический процесс с периодом τ = 40 лет задает главный исторический цикл и что определяет константа K – все это на данном уровне феноменологии так и остается неизвестным.
Что же такое сингулярность Дьяконова – Капицы?
В своей книге «Пути истории» И.М. Дьяконов рассматривает восемь фаз или ступеней исторического процесса: первобытную, первобытнообщинную, раннюю древность, имперскую древность, средневековье, абсолютистскую средневековую, капиталистическую и посткапиталистическую.
Фазы исторического развития периодизации Дьяконова хорошо соответствуют периодизации по алгоритму восьми шагов (таб. 2). Причем первобытную фазу, относящуюся к позднепалеолитическому периоду, можно считать фазой за номером нуль в теоретической периодизации; далее идут восемь исторических периодов по алгоритму и семь фаз Дьяконова.
Различие в том, что в теории имеется период 1386–1704 гг., отсутствующий в периодизации Дьяконова. И, кроме того, капиталистическая и посткапиталистическая фаза у И.М. Дьяконова ограничены 1840–1950, 1952–?? гг., тогда как по алгоритму – это 1863–1942, 1942–1982 и 1982–?? гг. Что выглядит привлекательнее, т. к. эти периоды неплохо соответствуют Кондратьевским циклам.
Важно отметить, что И.М. Дьяконов никогда не относился к результатам своих исследований как к догме. Это характерно для всех его работ. Можно ли в таком случае периодизацию по правилу восьми шагов считать совпадающей в пределах небольшой погрешности с периодизацией Дьяконова?
Понятно, что любой ответ на этот вопрос субъективен, мы же твердо убеждены в том, что это действительно так, столь велико совпадение независимых экспертных оценок с расчетными данными. В таком случае сингулярность Дьяконова – Капицы можно определить следующим образом:
Сингулярность Дьяконова – Капицы (историческая сингулярность), 2022 год, – это дата (точка) сингулярности эмпирической гиперболы мирового демографического роста необходимая наряду с датой начала неолита для расчета периодов мировой истории по правилу восьми шагов. К этой предельной точке на оси времени сходятся сокращающиеся по закону прогрессии исторические циклы. И это тот невидимый рубеж, за которым мировой исторический процесс переходит на совершенно новый, неизведанный путь развития.
Исторических циклов, задававших нарастающий темп развития человеческой цивилизации на протяжении последних десяти тысяч лет, за сингулярностью Дьяконова – Капицы – больше не будет. Что же нас ожидает за сингулярностью?
Что за сингулярностью?
Несомненно только то, что с глобальными историческими циклами будет полностью покончено. Очевидно, за сингулярностью Дьяконова – Капицы их продолжение – невозможно. Но что будет с инновационными циклами?
Ответить на этот вопрос, находясь в рамках феноменологической, чисто описательной теории нельзя, т. к. непонятна сама природа цикличности. Однако похоже, что Кондратьевский цикл каким-то непостижимым образом определяет как инновационные циклы, так и исторические. В таком случае за сингулярностью инновационных циклов также не будет. Более того, за сингулярностью Дьяконова – Капицы могут закончиться и одиннадцатилетние солнечные циклы!
Уж очень непохоже это явление на регулярный физический процесс. Достаточно вспомнить минимум Маундера, достоверность которого считается доказанной, когда в течение 70 лет с 1645-го по 1715 год – пятен на Солнце практически не было совсем! За сингулярностью Дьяконова – Капицы закончится рост численности населения Земли, а сама эта численность устремится к некоторой предельной, асимптотической величине.
Этот рост численности от неолита и до второй половины XX века, несомненно, был связан с цикличностью исторического процесса, о чем говорит эффективность алгоритма восьми шагов, но природа этой связи в рамках предложенной феноменологической схемы остается без объяснения.
* * *Ускорение развития цивилизации, связанное с ростом населения Земли (эта функциональная связь не является, очевидно, причинно-следственной), можно сравнить с ускорением состава на восьми последовательных участках железнодорожного пути.
Набор скорости продолжится и в ходе демографического перехода за сингулярностью Дьяконова – Капицы в течение еще одного цикла исторического времени. А затем, во второй половине XXI века, локомотив прогресса выйдет на магистраль (длина которой не определена) равномерного (не ускоренного) бескризисного развития.
Отсутствие ускорения в этой метафоре означает постоянство численности населения Земли, фиксированное энергопотребление, неизменность структуры сформировавшейся ноосферы; в последовательности: мифология, этика, эстетика, искусство, наука, техника, технология, сумма технологий – не будет новых членов. По сути, это будет КОНЕЦ ИСТОРИИ в привычном понимании смысла этого слова, т. е. как процесса циклического, ускоряющегося, качественно меняющегося, каким она, несомненно, во все времена и была: от неолита до наших дней.
Ускорения не будет, но темпы развития во всех областях человеческой деятельности будут максимальными, ранее невиданными – так что с концом роста численности населения Земли прогресс не закончится и творчество не исчезнет. Но грозит ли сингулярность какими-либо катастрофами? Никаких катаклизмов, связанных с завершением цикличности исторического процесса в 2022 году, ожидать не следует.
Ведь сингулярность Дьяконова – Капицы – сингулярность чисто математическая. Алгоритм восьми шагов закончил свою работу в 1982 году, но даже и тогда – в конце семидесятых, начале восьмидесятых годов прошлого века – в момент завершения последнего исторического цикла – никаких катастроф в масштабе биосферы не наблюдалось. А ведь это было время, не уступавшее по значимости времени начала неолита и представлявшее собой сжатую до предела эпоху перемен.
Есть и другие, не связанные с окончанием цикличности исторического процесса угрозы существованию цивилизации, по странному стечению обстоятельств приходящиеся по времени как раз на сингулярность Дьяконова – Капицы. Оптимистический взгляд в будущее на все времена обеспечивает позиция финализма.
Финализм и 25 сценариев конца света
Оптимистический взгляд на ближайшие перспективы развития цивилизации – редкость в наше время. А вот в катастрофических прогнозах недостатка нет. Прежде всего, отметим и исключим мнимый кризис планетарного цикла Панова, грозящий биосферной катастрофой в первой половине XXI века и описанный им в многочисленных публикациях. Кризис и катастрофа не состоятся по причине элементарных ошибок, допущенных А.Д. Пановым.
* * *Катастрофические потрясения в ближайшие десятилетия предсказывает выдающийся советский и российский ученый и популяризатор науки Л.М. Гиндилис в своей книге «SETI: Поиск Внеземного Разума», которая является продолжением бестселлера «Вселенная, жизнь, разум» И.С. Шкловского:
«Острота ситуации состоит в том, что коллапс должен наступить очень скоро, в первых десятилетиях XXI века. Поэтому, если бы даже человечество знало, как «повернуть» (или хотя бы приостановить) этот процесс, обладало бы средствами и волей для того, чтобы осуществить поворот уже сегодня, – у него просто не хватило бы времени, так как все негативные процессы обладают определенной инерцией, в силу которой их невозможно немедленно остановить…
Экономика Земли похожа на тяжело груженый транспорт, который на большой скорости мчится по бездорожью прямо к бездне. Видно, мы уже проскочили точку, где надо было свернуть, чтобы вписаться в «траекторию поворота».
И затормозить тоже не успеваем. Положение усугубляется тем, что никто не знает, где находятся руль и тормоз. Тем не менее и экипаж, и пассажиры настроены весьма благодушно, наивно полагая, что, «когда понадобится», они разберутся в устройстве транспорта и смогут совершить необходимый маневр.
Не думаю, что нарисованная картина означает непременную гибель человечества, хотя тяжкие испытания для нас, видимо, неизбежны. Если человечество сможет пройти через эти испытания, то характер развития должен коренным образом измениться».
Грядущий кризис, по мнению Л.М. Гиндилиса, – это кризис, прежде всего, нехватки ресурсов в момент перехода с гиперболического роста населения Земли на экспоненциальный. Этот переход, гипербола – экспонента, Гиндилис постулирует. Однако само представление о том, что гиперболический рост населения мира, природа которого, как отмечает и сам Л.М. Гиндилис, пока не ясна, сменится в первой половине XXI века экспоненциальным – не верно в принципе.
Дело в том, что при гиперболическом росте мировой естественный прирост пропорционален численности. По мере истощения ресурсов, с повышением плотности населения, или по каким-либо другим причинам, как считает Л.М. Гиндилис, он постепенно перестанет зависеть от численности и в определенный момент времени его можно уже будет считать постоянным. В этот момент и начнется, по мнению Л.М. Гиндилиса, краткая эпоха «коварного» экспоненциального роста и последующая за ней катастрофа.
Здесь Л.М. Гиндилис допускает серьезную ошибку, полагая, что человечество может рассматриваться как изолированная популяция, способная расти экспоненциально, т. е., считая его однородной массой с единым для всех ее частей естественным приростом. На самом деле – это конгломерат, образованный различными как по численности, так и по естественному приросту составляющими. Коэффициент естественного прироста в разные времена, для разных народов мог различаться в разы, поэтому никакое его усреднение по всей массе человечества не может считаться допустимым. Даже если считать, что численность каждого народа, этноса будет расти экспоненциально – из этого вовсе не следует, что численность человечества также будет расти экспоненциально.
При этом причина, по которой рост человечества многие тысячи лет происходил по закону гиперболы и которую нужно было бы понять до составления любых прогнозов – так и остается для него тайной за семью печатями. Кроме того, теорию демографического перехода, согласно которой численность населения мира в XXI веке стабилизируется и расти больше не будет, Л.М. Гиндилис вообще не рассматривает.
А ведь эта теория считается общепризнанной и подтверждена демографической историей стран, уже прошедших переход, и численность населения которых больше не растет. Ну, а раз нет и не будет «коварного» экспоненциального роста, а есть «выход на полку» (асимптотическая стабилизация за счет ООС) – то и катастроф никаких не будет. При стабилизации на уровне 8—10 млрд человек у человечества останутся в запасе многие сотни лет, чтобы разобраться с энергетическими, экологическими, экономическими, технологическими и прочими проблемами.
* * *Близкий конец света предрекают трансгуманисты в связи с приближающейся, по их мнению, технологической сингулярностью, а также популярные писатели от науки: Алексей Турчин в книге «Война и еще 25 сценариев конца света» и Александр Никонов в книге «Верхом на бомбе». Катастрофизм Турчина носит ярко выраженный физикалистский характер:
«В основе большинства сценариев глобальной катастрофы лежит „цепная реакция“ – иначе говоря, самоусиливающиеся процессы с нерегулируемой положительной обратной связью. Цепная реакция позволяет с помощью малых воздействий прийти к мощным изменениям: достаточно создать условия для возникновения самоусиливающегося процесса. Точно такой же принцип положительной обратной связи лежит и в основе механизма роста населения и роста потребления ресурсов. Чем больше население, тем быстрее оно растет, и тем больше оно потребляет ресурсов».
Катастрофы по Турчину и демографический рост по Коротаеву обусловлены одной и той же причиной: глобальными (общецивилизационными) положительными обратными связями. Но возможно ли такое в реальности? Турчин пишет:
«Однако чем больше население, тем более развитые технологии необходимы, чтобы поддерживать его жизнедеятельность, и тем более высокие технологии оно способно порождать, грубо говоря, за счет роста числа людей изобретателей. Таким образом, как показал А. Коротаев, скорость роста населения оказывается пропорциональна квадрату числа людей (dN/dt = N·N) [Коротаев, 2007]
Первое N в правой части этой формулы связано с ростом числа матерей, а второе – рост числа изобретателей. Решением этого дифференциального уравнения является гиперболическая кривая (достигающая бесконечности за конечное время, – а именно согласно вычислениям Форестера, в 2026 г. [Forester, 1960]). Гиперболически растущее население должно потреблять гиперболически увеличивающееся количество ресурсов, что несовместимо с принципиальной конечностью ресурсов материального мира».
Модель демографического роста, разработанная Коротаевым, основана на мифе о Мир-системе по Коротаеву, т. е. на предположении о существовании главного региона, в котором всегда проживала подавляющая часть населения мира и который представлял собой единую информационную систему. И мифе об изобретателях, благодаря усердию которых и обеспечивался этот взрывной гиперболический рост, причем во все времена, для всех этносов и на всех уровнях общественного и экономического развития. В такое трудно поверить, впрочем, как и во все другие положения демографической теории Коротаева.
Обрисовав безрадостное будущее нашей загибающейся, погрязшей в кризисах цивилизации, Турчин – и здесь нужно отдать ему должное – задается, наконец, вопросом:
«Интересно понять, какие силы препятствуют возникновению цепных реакций (положительных обратных связей, А.М.) – ведь в большинстве случаев в реальности глобальные катастрофы не происходят или ограничены по масштабам».
Если говорить о планетарном масштабе, то за всю историю цивилизации не было ни одного катастрофического, самоусиливающегося, с нерегулируемой положительной обратной связью процесса. Это реальность, так сказать, опытный факт. Катастрофы, конечно, случаются, но только локальные: как исключение, сбой в нормальном ходе процесса. Но если бы мир был устроен по Турчину – наша цивилизация давно прекратила бы свое существование.
Так, что же все-таки удерживает ее на плаву? Чтобы понять причину – нужно отказаться от физикалистского взгляда на прогресс и эволюцию. Ответом может быть финализм, финалистическое видение проблемы. И как проявление финализма на каждом этапе становления биосферы и ноосферы – эквифинальность циклических природных и социальных процессов, последовательно продвигающих развивающуюся систему на пути к финалу.
Эквифинальность выступает здесь как особая парадоксальная системность, встроенная система интеллектуального регулирования (управления), присущая биосфере и ноосфере. Эквифинальность – это способность биологической, социальной системы достигать целевых, финальных состояний различными путями независимо от начальных и/или текущих условий процесса. Термин эквифинальность впервые появился в биологии, а сейчас используется в медицине, экономике, менеджменте, экологии…
Чем же эквифинальность биологических и социально-экономических систем отличается от гомеорезиса кибернетических систем, моделирующих первые и состоящих из подсистем, охваченных контурами отрицательных и положительных обратных связей? Гомеорезис – это динамический гомеостазис, т. е. поддержка устойчивости, надежности динамического процесса. Это свойство относительно простых систем, которые могут быть описаны и представлены графически в виде подсистем с обратными связями.
Причины же эквифинальности зачастую непонятны и загадочны и могут проявляться в виде парадоксальной системности чрезвычайно сложных объектов таких, например, как биосфера Земли, когда существующие обратные связи столь многочисленны и сложны, что учесть их все чрезвычайно трудно или даже в принципе невозможно.
Ярким примером эквифинальности на социальном уровне является экономический цикл (любой из существующих), все фазы которого реализуются в обязательном порядке, причем причины его порождающие, а, точнее комплекс причин, могут находиться на совершенно разных уровнях организации общества:
«Весьма вероятно, что экономический цикл не был бы вызван к жизни если бы эти «активные» силы (изменения урожайности, изобретения, изменения в спросе и т. д.) отсутствовали, или если бы изменилась одна или несколько важных черт в экономической институциональной структуре, или если, например, заработная плата и условия заключения сделок были бы вполне эластичными.
Если бы предприниматели вели себя каким-либо иным образом, если бы они обладали способностью безошибочного предвидения конъюнктуры, или если бы организация денежной системы была другой и финансовые органы предприняли бы шаги для предотвращения последствий воздействия этих „активных“ сил; словом, если бы все эти факторы действовали не так, как они действовали на самом деле» [52].



