
Полная версия:
Приключения Майкла и Константина
Но за пределами всего этого стоит недостижимый кардинал. Его невозможно достичь никакими преобразованиями снизу. Концептуальный скачок от ничего до первой бесконечности – то же самое, что скачок от первой бесконечности до недостижимого кардинала.
∞n, < недостижимость (inaccessible) где n – любая мыслимая мощность бесконечности.
Существует такое множество, величину которого нельзя описать принятым ранее математическим языком. Такое множество называют неописуемой недостижимостью (Indescribable Inaccessible). Такую недостижимость мы даже не можем выразить, используя значок "∞", как мы сделали это с обычной недостижимостью, ведь согласно определению – это невозможно. Математики лишь утверждают, что:
Недостижимость < Неописуемая недостижимость.
И всё изложенное выше содержится лишь в среднем нарративе бесконечно малой частицы. В одном из таких средних нарративов содержится также алеф-бесконечность пространственных измерений, недостижимый кардинал измерений и т.д. В общем, там находится всё, что было написано ранее в виде измерений.
В математике есть и другие придуманные аксиомы, которые создают ещё большие недостижимости. Вот их неполный перечень, расставленный в порядке возрастания:
недостижимость (INACCESSIBLE)
гипер-недостижимость (HYPER-INACCESSIBLE)
n-гипер-недостижимость (N-HYPER-INACCESSIBLE)
слабо компактная недостижимость (WEAKLY COMPACT INACCESSIBLE)
неописуемая недостижимость (INDESCRIBABLE INACCESSIBLE)
несворачиваемая недостижимость (UNFOLDABLE INACCESSIBLE)
итерируемая недостижимость (INEFFABLE INACCESSIBLE)
рамсеевкая недостижимость (RAMSEY INACCESSIBLE)
измеримая недостижимость (MEASURABLE INACCESSIBLE)
сильная недостижимость (STRONG INACCESSIBLE)
сильно компактная недостижимость (STRONGLY COMPACT INACCESSIBLE)
сверхсильная недостижимость (SUPERSTRONG INACCESSIBLE)
сверхкомпактная недостижимость (SUPERCOMPACT INACCESSIBLE)
расширяемая недостижимость (EXTENDIBLE INACCESSIBLE)
n-сверхсильная недостижимость (N-SUPERSTRONG INACCESSIBLE)
почти гигантская недостижимость (ALMOST HUGE INACCESSIBLE)
гигантская недостижимость (HUGE INACCESSIBLE)
сверхгигантская недостижимость (SUPERHUGE INACCESSIBLE)
n-гигантская недостижимость (N-HUGE INACCESSIBLE)
разрядовая недостижимость (RANK-INTO-RANK INACCESSIBLE)
Но давайте не забегать вперёд.
Махло кардинал – это кардинал, для которого множество всех возможных регулярных кардиналов меньших него стационарно. Разберём детальнее, что это значит. Для каждой последовательности регулярных кардиналов можно определить предельный кардинал, который так же будет предельным ординалом:
ℵ0, ℵ1, ℵ2, ℵ3, …, ℵω
I, ℵI+1, ℵI+2, ℵI+3, …, ℵI+ω
I2, ℵI2+1, ℵI2+2, ℵI2+3, …, ℵI2+ω
I, I2, I3, I4, …, Iω
I(2,0), I(2,1), I(2,2), I(2,3), …, I(2,ω)
I(1,0), I(2,0), I(3,0), I(4,0), …, ψI(ω,0)(0)
I(1,0), I(1,0,0), I(1,0,0,0), I(1,0,0,0,0), …, ψI(1ω)(0)
Тогда Махло кардинал, будет таким, который будет больше любого такого предельного кардинала, так чтобы множество регулярных кардиналов было для него стационарным. То есть Махло кардинал является пределом для всех регулярных ординалов меньше него, но и для их клубного сомножества предельных ординалов Махло кардинал тоже будет пределом, являясь бо́льшим по отношению к каждому члену этого клуба. Из этого следует, что по своим свойствам Махло кардинал так же должен быть регулярным, то есть соответствовать требованию: cf(М) = М (здесь и далее, будем обозначать Махло кардинал и соответствующий ему минимальный ординал большой буквой М). Регулярность Махло кардинала доказывается от обратного, вкратце, если бы он не был регулярным, то должен был бы существовать меньший по величине регулярный ординал, с помощью которого его можно было бы образовать, и тогда он являлся бы частью клуба предельных кардиналов, но как мы помним по определению он является для всех них пределом, значит не входит в их множество, и следовательно больше их. Ну а раз Махло кардинал является регулярным и при этом он предел, значит он так же предельный, тогда получается что по своим свойствам он ещё и недостижимый (которые по определению регулярные и предельные одновременно). Тем не менее, он будет больше любого ранее определённого нами недостижимого кардинала или гипер-недостижимого кардинала с любой мыслимой степенью недостижимости (потому что они всегда регулярные, а значит где-то за ними есть предельный кардинал из клубного сомножества; Махло кардинал же по определению является пределом и для тех и для других). Получается что множество всех мыслимых недостижимых и гипер-недостижимых кардиналов меньших него так же стационарно для Махло кардинала, как и множество всех регулярных кардиналов меньше него. То есть уже нет никаких сомнений, что Махло кардинал будет больше любого недостижимого, которого мы способны выразить с помощью иерархии Веблена, или какой-либо иной иерархии, способной учитывать степени недостижимости. Значит он идеально подходит нам в качестве диагонализатора для ординальной коллапсирующей функции.
Махло кардинал для которого стационарно множество регулярных алеф-кардиналов (и соответственно слабонедостижимых тоже) будет называться Слабым Махло кардиналом, а Махло кардинал для которого стационарно множество регулярных бет-кардиналов (и соответственно сильнонедостижимых тоже) будет называться Сильным Махло кардиналом. Если предположить правильность континуум-гипотезы, то Слабый Махло кардинал и Сильный Махло кардинал это один и то же кардинал, однако если предположить ложность континуум-гипотезы, то так же как это было с недостижимыми: Слабый Махло кардинал < Сильный Махло кардинал, и мы так же не можем предположить насколько первый меньше второго, он может быть даже меньше континуума (ב1).
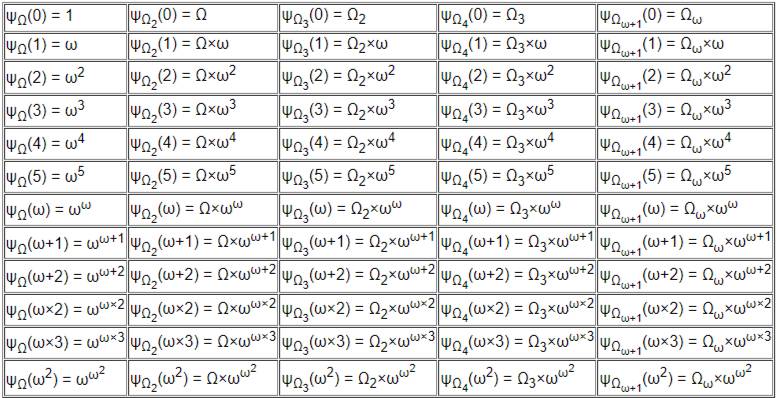
Функция Бухольца принимала в себя два аргумента: ψπ(n) – где π – это регулярный кардинал, на основе которого происходит коллапсирование, а n – это ординал, основной аргумент функции, который собственно и коллапсируется, он может быть любым, но не должен превосходить по кардинальности π. В целом функция ψπ(n), в случае |n| = π, на выходе понижала кардинальность n, но увеличивала рекурсию получившегося ординала, так что ψΩk+1(Ωk+1) = εΩk+1, и ψΩk(Ωk+α) = ωψΩk(Ωk)+α.
Здесь придём к функции Ратъена. На самом деле это не одна, а целых две функции, и кроме ψ-функции Ратъен определил еще и χ-функцию. Принципиальное отличие между ними заключается в том, что если ψ-функция возвращает любые ординалы, то χ-функция возвращает всегда только регулярные ординалы. По определению, если n < I, то χ(n) – возвращает n-ный несчетный регулярный ординал (считая с нуля). Тут важно отметить, что ω-ный регулярный ординал это ωω+1, потому что, как вы должны помнить из прошлой части, |ωω| = ℵω – регулярным не является. Следовательно, пользуясь обозначениями коллапсирующей функции, мы получим следующие преобразования: χ(0) = Ω, χ(1) = Ω2, χ(2) = Ω3, χ(ω) = Ωω+1, χ(Ω) = χ(χ(0)) = ΩΩ+1, χ(Ω) = χ(χ(1)) = ΩΩ+2, χ(ΩΩΩΩ…) = Ω(ΩΩΩ…+1) = ΩФ(1,0)+1, и т.д. В целом, принципы коллапсирования позволяют определить общее свойство χ(n) = Ωn+1, гласящее что n-ный несчётный кардинал равен кардиналу, который предшествует n-ному несчетному регулярному кардиналу. Однако работает это свойство только пока аргумент функции меньше недостижимого кардинала (n < I).
Общее свойство коллапсирования теперь стало следующим:
ψχ(k)(α) = ωΩk+β, где α = k+β – если α > k, k – предельный ординал или ноль.
ψχ(k)(α) = ωΩk+β+1, где α = k+β – если α > k, k – очередной ординал.
ψχ(k)(α) = ωΩα – если α ≤ k, k – предельный ординал или ноль.
ψχ(k)(α) = ωΩα+1 – если α ≤ k, k – очередной ординал.
Бесконечно тетрированный Махло ординал в виде бесконечной степенной башни внутри функции Ратъена, который также можно записать как ψ(εM+1), это особенный ординал, который носит имя Ординал Ратъена.
Майкл и Константин случайно наткнулись на мир, соответствующий этим математическим требованиям.
Майкл и Константин решили отдохнуть от исследований и телепортировались в другое измерение для развлечения. Их приключения начались с первого прыжка в параллельное измерение, где они обнаружили совершенно новые ландшафты и создания. В одном из измерений они оказались в мире, где все предметы обладали живым сознанием. Они познакомились с деревьями, которые могли говорить и дарить свои советы, и с реками, которые имели свои настроения и эмоции. Майкл и Константин провели много времени, изучая этот удивительный мир и узнавая о его уникальных особенностях. Казалось бы, всё отлично, но…
– Если вы одушевлённые, что тогда у вас неодушевлённое? – С интересом спросил Майкл
– Вы имеете ввиду животных? – Поинтересовалось дерево.
– “Животных”?! У вас животные и растения поменялись местами? А что насчёт людей? Вы используете их как стол? – Съязвил Майкл Браун.
– Не, у нас люди крайне многофункциональны, например, из крови мы делаем вино, а вам то это виднее, потому что я очень пьяно. Мне видятся ожившие люди – Сказало дерево решив, что оно словило белочку.
– А этот мир всё-таки криповый, если разобраться – Подметил Константин.
Майкл и Константин решили прогуляться по миру, но все предметы увидев их, резко запаниковали.
– Не с места! А то стрелять буду! – Пригрозил пистолет
– Я думаю, жалкие гномики, которые вылетают из твоего лица, желая принять наше существование близко к сердцу не остановят нас. – С нахальной улыбкой крикнул Константин в ответ.
– Мы вовсе не гномы, дылда ты паранормальная! Мозгов у тебя походу нет, раз ты так высказываешься пистолету при исполнении. А жаль, так хотелось их превратить в вкуснейшую кашицу – Высоким голоском сказала пуля, залезая в дуло пистолета.
Пистолет издал громоподобный выстрел, но сила Константина была настолько могуча, что взмахнув рукой он создал порыв ветра, вернувший пулю обратно в дуло, взорвав живой пистолет на кусочки.
– У меня есть некое подозрение что нам тут не рады, – сказал Майкл и учёные ушли отсюда.
Учёные отправились в почти самый высший нарратив бесконечно малой частицы. И в нём они нашли суперкомпактный (сверхкомпактный) кардинал.
Суперкомпактный кардинал – это концепция из теории множеств, раздела математики, который имеет дело с наборами объектов, называемых множествами. В частности, суперкомпактные кардиналы – это большие кардиналы, которые обладают определёнными свойствами, которые делают их полезными для установления результатов согласованности в рамках теории множеств и для изучения структуры теоретико-множественной вселенной.
Кардинальное число κ считается суперкомпактным, если оно обладает следующим свойством: для любого набора структур {M}, каждая из которых имеет размер меньше, чем κ, и любого унарного предиката (свойства элементов) φ, существует элементарное вложение из вселенной V в более крупную структуру N, такое, что N является структурой размера κ, φ выполняется для элемента из N тогда и только тогда, когда оно выполняется для элемента из V, а критическая точка (наименьший порядковый номер, перемещаемый вложением) меньше, чем κ.
Проще говоря, кардинальное число κ является суперкомпактным, если оно достаточно велико, чтобы любое свойство (описываемое унарным предикатом), которое справедливо для структур меньшего размера, могло быть сохранено и расширено до структуры большего размера κ.
Расширяемый кардинал – это понятие из теории множеств, в частности, из области аксиом большого кардинала. Это утверждения, утверждающие существование определенных видов больших кардинальных чисел с определенными свойствами. Концепция расширяемого кардинала относится к изучению согласованности и структуры математической вселенной, особенно в рамках теории множеств.
Кардинальное число κ считается расширяемым, если существует нетривиальное элементарное вложение j из вселенной V в транзитивную внутреннюю модель M такое, что j (κ) > κ. Здесь "нетривиальный" означает, что вложение не является тождественным отображением, а "элементарное вложение" подразумевает, что вложение сохраняет все утверждения первого порядка о множествах. Проще говоря, расширяемый кардинал κ достаточно велик, чтобы существовал способ "растянуть" универсум за пределы κ значимым образом.
Измеримый кардинал является фундаментальным понятием в теории множеств, особенно в области аксиом больших кардиналов. Эти аксиомы предполагают существование определенных типов больших кардиналов со специфическими свойствами. Измеримые кардиналы особенно важны из-за их глубокого значения для структуры и согласованности теории множеств и математики в целом.
Кардинальное число κ считается измеримым, если существует неосновной κ-полный ультрафильтр (также известный как мера) на множестве степеней κ. Проще говоря, измеримый кардинал κ достаточно велик, чтобы существовал способ определить нетривиальное понятие "размера" или "объёма" для подмножеств κ, удовлетворяющих определённым свойствам.
Но в конце концов учёные поднялись до самой вершины бесконечно малой частицы и, к их большому удивлению, они обнаружили нечто невероятное – существо, которое они назвали Богом Микроляндии. Встреча учёных Майкла и Константина с Богом Микроляндии была одним из самых удивительных и захватывающих моментов в их научной карьере. Они не видели бога, но могли общаться с ним.
Бог Микроляндии оказался существом с высоким самомнением и непомерным эго. Он утверждал, что является источником всей энергии и создателем всего мира. Он считал себя непревзойдённым и непостижимым, и не признавал никакой власти или авторитета.
– Итак, ты утверждаешь, что создал всё существующее, и нет никого выше тебя? – Подытожил Константин.
– Верно, дитя моё. Я создал всё, я создал всех вас. Вы удостоены великой чести общаться с вашим творцом. Я управляю вашими жизнями, вашим сознанием, вашей сущностью. – Отвечал спокойным божественным голосом Бог Микроляндии.
– Но чем ты являешься? Я имею ввиду, есть выражения, такие как “Бог есть любовь” и прочая ерунда…
– Ваш разум не способен воспринять моё бытие. Вы можете знать только, чем я не являюсь. Любые концепции неприменимы по отношению ко мне, ибо я стою за пределами всего. Творение не способно познать своего творца.
Майкл и Константин были поражены этим открытием. Они не только столкнулись с новым видом существа, но и столкнулись с его невероятным самомнением. Они понимали, что это открытие может иметь огромное значение для науки и философии, и решили продолжить исследование Бога Микроляндии. Учёные знали об апофатическом богословии, но не ожидали обнаружить его так скоро.
Они провели долгие часы в общении с Богом Микроляндии, задавая ему вопросы о происхождении Вселенной, физических законах и смысле жизни. Хотя Бог Микроляндии продолжал утверждать свою непостижимость, он также начал задумываться о своей роли во Вселенной и о возможности существования других существ, равных ему.
В результате этой встречи, Майкл и Константин расширили свои знания о фундаментальных законах природы и философии, а также получили новые перспективы на исследование Вселенной. Они продолжали свою научную работу, используя полученные знания и опыт, чтобы продвигаться вперёд и открывать новые горизонты в науке.
Глава 2
– Вам нельзя здесь копать! – Охранник, насупившись, окликнул Константина.
Раздался выстрел, воспроизведший футуристичный плазменный звук. Охранник начал интенсивно дрожать, а из его тела обильно выделялся пот. Через пару секунд он упал на землю без сознания. Константин подошёл к месту, которое заприметил для раскопки. К нему подбежал Майкл.
– Зачем ты сделал это?! Ты убил его! – Негодовал он.
– Да не парься, он просто в отключке. Через 12 часов эффект пройдёт, и он вновь встанет на ноги. А пока пусть немного поваляется. – С беспечной улыбкой произнёс Константин, начиная размечать территорию.
– А если его съедят дикие звери? – Не успокаивался Майкл.
– Да что ты заладил всё, никак не уймёшься! Вот и стереги его, если так хочется, а мне не мешай. – Бросил учёный, начиная рыть размеченный кубометр земли мощным лазерным буром глубоко вниз.
С помощью лазерного бура, Константин пробивался сквозь слои земли, преодолевая все преграды на своем пути. Но когда он достиг предполагаемой глубины ядра планеты, он обнаружил нечто неожиданное – он находился в другом измерении. Вместо ожидаемого ядра планеты, он оказался в странном и неопознанном мире.
Константин был ошеломлен и немного разочарован, но его научное любопытство превышало разочарование. Он решил использовать эту неожиданность в свою пользу и исследовать новое измерение, в котором оказался. Учёный был уверен, что здесь он может найти нечто ценное и уникальное.
Константин начал свои исследования в новом измерении, надеясь найти редкий материал, известный как нихоний. Он исследовал незнакомые ландшафты, изучал новые формы жизни и собирал образцы неизвестных минералов. Он открыл множество ценных и полезных материалов, которые были уникальны для этого измерения, хотя он не нашёл нихоний в ядре планеты, как ожидалось. Он нашёл ксерантий-металл, который при взаимодействии с телом отправляет импульсы в мозг отвечающие за агрессию. Вдруг он неожиданно увидел исследовательскую группу, которая устроила настоящие бои на выживание. В этом бое многие люди получили ранения несовместимые с жизнью.
Учёный Константин понял, что его экспедиция не прошла напрасно. Он получил новые знания и открыл новые возможности для науки. Его открытия помогли расширить границы нашего понимания о мире и показали, что даже в неожиданных ситуациях можно найти ценные сокровища.
Константин вдруг с ужасом понял, что забыл об их с Майклом путешествии внутрь элементарных частиц вымысла и вспомнил об этом только сейчас. Он думал, что находится в своей реальности. “Неужели я схожу с ума”, подумал учёный. “Надо спросить у Майкла, что с этим делать”.
– Ты живёшь уже более тысячи лет, из-за законов твоей вселенной при такой долгой жизни у человека начинаются проблемы с памятью, так как его мозг не предназначен для столь долгой работы. Ничего страшного, я могу внести кое-какие изменения в твой мозг. – Доктор Браун прописал Константину операцию на мозг.
Операция прошла успешно и Константин снова здоров. Он вспомнил всё: и своё прошлое, и свой незаурядный интеллект, что позволило ему вновь быть умным; и его цели.
Глава 3
Учёные вновь вернулись к исследованиям после небольшого отдыха. Они закончили с бесконечно малой частицей и сосредоточили свое внимание на исследовании бозона Хиггса – ключевой частицы, которая играет важную роль в объяснении происхождения массы элементарных частиц. В ходе своих экспериментов они обнаружили нечто удивительное – Бозон Хиггса не ограничен пространством и временем, а также содержит гиперкомпактный кардинал.
Вначале они провели серию экспериментов с использованием сложных математических моделей и теорий, чтобы изучить свойства бозона Хиггса. Они использовали методы математического анализа и статистики для обработки полученных данных и выявления закономерностей.
После тщательного анализа результатов экспериментов Майкл и Константин заметили некоторые необычные математические закономерности, которые не могли быть объяснены с помощью стандартных теорий. Они решили глубже исследовать эти закономерности и их связь с бозоном Хиггса.
Для этого они обратились к теории множеств и теории чисел, применяя математические методы и концепции, чтобы выяснить действие гиперкомпактного кардинала. Они провели дополнительные математические вычисления и моделирование, чтобы понять его влияние на бозон Хиггса.
– Гиперкомпактный кардинал – это особенно сильный большой кардинал. – Начал своё объяснение Доктор Браун. – Он принадлежит к иерархии особо крупных кардиналов, каждый из которых обладает своими собственными определяющими свойствами. Кардинальное число κ считается Гиперкомпактным, если оно обладает определенными свойствами, связанными с элементарными вложениями.
– Вот некоторые ключевые концепции, связанные с Гиперкомпактными кардиналами: – Продолжил Константин. – Элементарное вложение: Учитывая две структуры, подобные множествам (такие как структуры заданного размера, представляющие универсум множеств), элементарное вложение является своего рода гомоморфизмом, который сохраняет истинность логических утверждений первого порядка. Критическая точка: Для гиперкомпактной кардинальной величины κ существует определенный порядковый номер, называемый критической точкой, обозначаемый crit(j), где j – элементарное вложение, связанное с κ. Критическая точка – это наименьший порядковый номер, отображенный нетривиально с помощью вложения. Прочность: Гиперкомпактные кардиналы подразумевают определенный уровень "прочности" в своем существовании. Неофициально это означает, что присутствуют определенные свойства крупных кардиналов, делающие кардинал более могущественным в иерархии крупных кардиналов.
– Итак, мы исследовали лишь математическую составляющую. Надо проверить, имеет ли место быть здесь философия.
После тщательных проверок они убедились и в существовании философии тоже.
– Интересно, здесь нет большинства известных нам философских принципов, а вместо них какие-то хаотические каракули, которые сложно разобрать, но я нашёл обычные и платонические концепции! – Сказал Константин. – Обычные концепции и платонические концепции являются двумя разными подходами к пониманию и объяснению реальности и ее фундаментальных принципов. Обычные концепции, также известные как эмпирические концепции, основаны на наблюдении и опыте. Они строятся на основе конкретных объектов, явлений и событий, которые мы встречаем в нашей повседневной жизни. Обычные концепции основываются на том, что мы можем наблюдать и измерять, и они обычно связаны с конкретными материальными объектами или явлениями. Например, концепция "стол" связана с наблюдаемым объектом, который мы используем для размещения предметов.
– С другой стороны, – продолжил Майкл Браун, – платонические концепции, также известные как идеальные концепции, основаны на вере в существование абстрактных идеальных форм или понятий, которые превосходят нашу конкретную реальность. Платонические концепции предполагают, что существуют всеобщие идеи, которые являются идеальными и неизменными, и они являются основой для конкретных объектов или явлений, которые мы наблюдаем. Например, платоническая концепция "красоты" предполагает существование идеальной формы красоты, которая является идеальной и неизменной, и которая служит основой для всех конкретных объектов или явлений, которые мы считаем красивыми. Но самая лучшая и важная платоническая концепция, по мнению самого Платона, это платоническая концепция “Добра”. Оно также может быть истолковано как Совершенство или просто Хорошее.
Таким образом, основное различие между обычными и платоническими концепциями заключается в их источнике и природе. Обычные концепции основываются на наблюдении и опыте, связаны с конкретными объектами и явлениями, которые мы встречаем в нашей повседневной жизни. В то время как платонические концепции основываются на идеях и абстрактных формах, которые предполагаются существовать вне нашей конкретной реальности и служат основой для конкретных объектов и явлений. Соответственно, эти платонические концепции на самом деле существуют за пределами бозона Хиггса.
Учёные пошли спать.
Глава 4
Майкл и Константин были давними друзьями, которые любили проводить время вместе, обсуждая философию, науку и устраивая ночные философские посиделки. Они обсуждали и экспериментировали с патафизикой, Римановым многообразием, а также исследовали саму суть Расширенной Терминологии.
– Для обозначения расширения используются приставки супер-, мега-, гипер-, омни-, и т.д. – начал Константин. – В самом базовом смысле, приставка "супер-" будет обозначать отличие объекта от исходного настолько, что изначальный объект будет неизмеримо слабее, чем супер, а супер объект будет превосходить абсолютно все аспекты обычного объекта неизмеримо соответственно. Например, супер-защита настолько сильнее, чем защита, что какое бы мы свойство защиты не применили для описания супер-защиты, оно будет бесполезно, ибо супер-защита намного за пределами чего-либо, что мы знаем о защите. Приставка мега-, в свою очередь, превосходит супер- так же, как супер- превосходит обычную концепцию, и дальше уже понятно. Приставок может быть абсолютно бесконечно.

