
Полная версия:
Объектно-ориентированное программирование на Java. Платформа Java SE
Вы также можете не обрабатывать исключения блоком try-catch в методе, а передать это право вызывающему этот метод.

В этом случае вы используете ключевое слово throws, которое прописывается в сигнатуре метода, и обозначающее что этот метод потенциально может выбросить исключение с указанным типом.
И уже в вызывающем коде обработать вызов этого метода блоком try-catch.
Также вы можете сами, специально, не виртуальная машина, а вы – выбросить исключение с помощью ключевого слова throw, указав тип исключения.

Например, чтобы предотвратить выполнение кода, когда параметр метода не является возможным входным значением.
Таким образом, ключевое слово throw – служит для генерации исключений.
Блок try может иметь несколько блоков catch, каждый из которых имеет дело с конкретным исключением.

Если блок try генерирует исключение, то соответствующий блок catch обработает исключение, и программа будет продолжена.
Встроенные исключения Java имеют определенную иерархию.
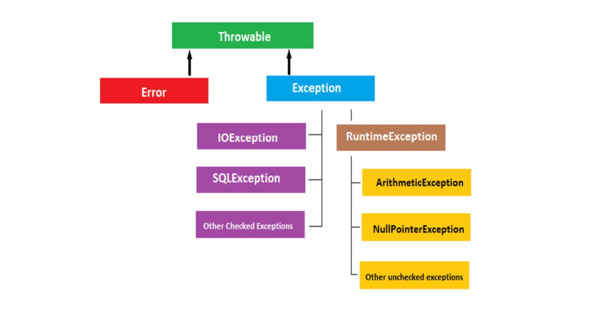
Все классы, представляющие ошибки являются наследниками класса java.lang.Throwable.
Только объекты этого класса или его наследников могут быть «выброшены» JVM при возникновении какой-нибудь исключительной ситуации, а также только эти исключения могут быть «выброшены» во время выполнения программы с помощью ключевого слова throw.
Поэтому, если вы хотите создать свой класс исключения, он должен происходить от класса Throwable, или более точнее от класса Exception.
Также нужно учитывать, что все исключения делятся на «проверяемые» (checked) и «непроверяемые» (unchecked).
checked exception – проверяемое исключение, которое проверяется компилятором.
Throwable и Exception и все их наследники, за исключением наследников Error-а и RuntimeException – проверяемые.
Error и RuntimeException и все их наследники – не проверяемые компилятором исключения.
Компилятор при компиляции проверяет код на возможность выброса при выполнении кода проверяемого исключения.
И так как проверяемое исключение проверяется во время компиляции, возникнет ошибка компиляции, если проверяемое исключение не обработано блоком try-catch, или оно не объявлено в заголовке или сигнатуре метода с помощью ключевого слова throws.

Так почему не все исключения являются проверяемыми?
Дело в том, что если проверять каждое место, где теоретически может быть ошибка, то ваш код сильно разрастется, и станет плохо читаемым.
И язык Java будет полностью непригодным для использования в качестве языка программирования.
Например, в любом месте, где происходит деление чисел, нужно было бы проверять на исключение ArithmeticException, потому что возможно деление на ноль.
Эту проверку создатели языка оставили программисту на его усмотрение.
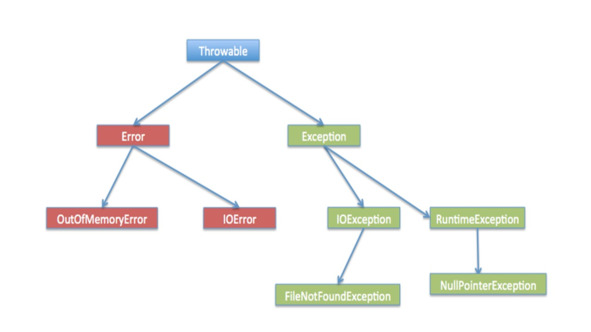
Таким образом, исключение RuntimeException является не проверяемым и выбрасывается во время выполнения Java кода, и его дочерние исключения также являются не проверяемыми.
Это исключение IndexOutOfBoundsException – выбрасывается, когда индекс некоторого элемента в структуре данных не попадает в диапазон имеющихся индексов.
Исключение NullPointerException – выбрасывается, когда ссылка на объект, к которому вы обращаетесь, хранит null.
Исключение ClassCastException – это ошибка приведения типов.
И исключение ArithmeticException – выбрасывается, когда выполняются недопустимые арифметические операции, например, деление на ноль.
Исключение Error также является не проверяемым, которое показывает серьезные проблемы возникающие во время выполнения приложения. Исключение Error сигнализирует о ненормальном ходе выполнения программы, т.е. о каких-то критических проблемах.
И его дочерние исключения, также не проверяемые, ThreadDeath – вызывается при неожиданной остановке потока.
Исключение StackOverflowError – ошибка переполнение стека. Часто возникает в рекурсивных функциях из-за неправильного условия выхода.
И исключение OutOfMemoryError – ошибка переполнения памяти.
Из описания этих не проверяемых исключений видно, что обработать все эти возможные ситуации в коде невозможно, иначе весь код – это будет сплошной try-catch.
Теперь, при использовании множественных операторов catch обработчики подклассов исключений должные находиться выше, чем обработчики их суперклассов.
Иначе, суперкласс будет перехватывать все исключения, имея большую область перехвата.
Иными словами, Exception не должен находиться выше ArithmeticException и ArrayIndexOutOfBoundsException.
И еще, операторы try могут быть вложенными.
Если вложенный оператор try не имеет своего обработчика catch для определения исключения, то идёт поиск обработчика catch у внешнего блока try и т. д.
Если подходящий catch не будет найден, то исключение обработает сама система завершением программы.
Таким образом, проверка на проверяемые исключения происходит в момент компиляции, а перехват исключений блоком catch происходит в момент выполнения кода.
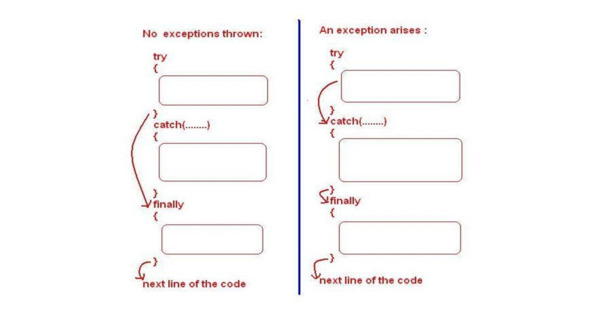
Теперь, есть еще одна конструкция в обработке исключений, это блок finally.
Когда исключение передано, выполнение метода направляется по нелинейному пути.
Это может стать источником проблем.
Например, при входе метод открывает файл и закрывает при выходе.
Чтобы закрытие файла не было пропущено из-за обработки исключения, используется блок finally.
Ключевое слово finally создаёт блок кода, который будет выполнен после завершения блока try/catch, но перед кодом, следующим за ним.
Блок будет выполнен, независимо от того, передано исключение или нет.
Оператор finally не обязателен, однако каждый оператор try требует наличия либо catch, либо finally.
Таким образом, блок finally всегда выполняется, когда блок try завершается.
Это гарантирует, что блок finally будет выполнен, даже если произойдет непредвиденное исключение.
Также блок finally позволяет программисту избежать случайного обхода нужного кода.
Включение необходимого для выполнения кода в блок finally всегда является хорошей практикой, даже если не ожидается никаких исключений.
Однако блок finally не всегда может выполняться.
Если виртуальная машина JVM завершает работу во время выполнения кода try или catch, блок finally может не выполняться.
Аналогично, если поток, выполняющий код try или catch, прерывается или убивается, блок finally может не выполняться, даже если программа в целом продолжается.
Блок finally – это ключевой инструмент для предотвращения утечек ресурсов.
Закрывая файл или восстанавливая ресурсы, поместите код в блок finally, чтобы гарантировать, выполнение необходимых операций.
Рассмотрим этот пример.

Каким здесь может быть вывод в консоль?
Здесь вполне возможна ситуация, когда в консоль сначала будет выведено сообщение об ошибке, а только потом вывод System.out.println.
Так как вывод System. out является буферизированным, то есть сообщения сначала помещаются в буфер, прежде они будут выведены в консоль.
А сообщение необработанного исключение выводится через не буферизированный вывод System.err.
Как уже было сказано, каждый оператор try требует наличия либо catch, либо finally.

Поэтому возможна конструкция try – finally.
И блок finally получит управление, даже если try-блок завершится исключением.
И блок finally получит управление, даже если try-блок завершится директивой выхода из метода.
Однако блок finally НЕ будет вызываться, если мы убъем виртуальную машину JVM.
При всем при этом, надо отметить, что блок finally не перехватывает исключение, и программа завершиться ошибкой при возникновении в блоке try исключения.
Исключение перехватывает только блок catch.
Таким образом мы разобрали почти все случаи работы операторов try, catch, throws, throw, и finally.
Рекурсия

В некоторых случаях нам нужно выполнять повторные вычисления.
И мы видели циклы for и while, которые выполняют повторные вычисления.
Теперь мы увидим гораздо более мощный механизм повторных вычислений, который называется рекурсией.
Ранее мы определили метод square, который, принимая целое число, возвращает квадрат числа.
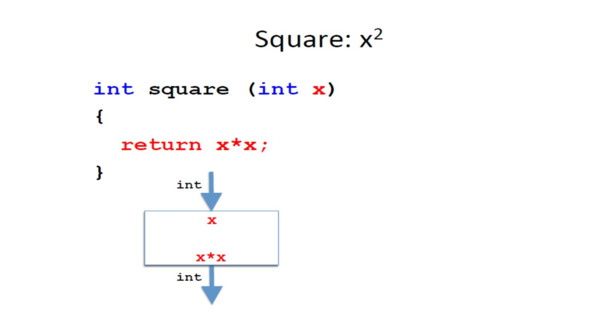
Теперь мы хотели бы определить метод, который возводит в степень.
Мы хотим определить метод, который, учитывая базу x и показатель y, вычисляет x в степени y.
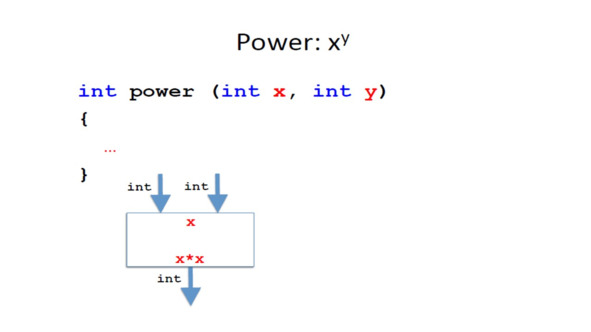
Поэтому, если y равно 2, мы вычисляем квадрат числа, как и раньше.
Вы видите, что в этом методе мы имеем два аргумента, целые числа x и y.
Давайте сначала попытаемся определить этот метод.
Давайте проанализируем несколько случаев.
Если y равно 0, то результат x равен степени 0, т. е. 1.
Если y равно 1, результат будет сразу x.
Если y равно 2, результатом является квадрат x.
Мы можем вызвать метод square, который мы определили ранее.
Если y равно 3, мы имеем x в кубе, предполагая, что у нас есть метод, называемый cube, определенный заранее.
И далее нам понадобятся другие методы для всех различных значений y, которые могут быть приняты.

Теперь мы можем заменить вызовы методов square, cube, и т. д. следующим кодом.
Таким образом, мы будем иметь x умножить на x, x умножить на x умножить на x и т. д.

Сейчас это немного лучше, но все же очень плохо, потому что порождает бесконечный код.
Но мы все же кое-чему научились.
Чтобы вычислить x в степени y, мы должны умножить x y раз.
Но мы должны учитывать, является ли эта процедура применима для всех целых чисел y?
Нет.
Только для y больше или равно 0.
Для отрицательного y нам понадобится другой способ умножения.
Если у нас есть повторное умножение, мы можем использовать цикл.

Вот пример того, как мы можем это сделать.
Мы инициализируем целочисленную переменную z в 1, а затем вводим цикл.
Счетчик i инициализируется 1 и увеличивается на 1 при каждом прогоне цикла.
Этот счетчик отслеживает, сколько х мы умножаем и накапливаем с помощью z.
И мы должны выполнять тело цикла ровно y раз, пока i не станет равен y.
Затем мы выходим и возвращаем накопленное значение в z.
Давайте проанализируем это снова.

x в степени y равно 1, если y равно 0.
А если y строго больше 0, то x в степени y равно x умножить на x в степени y минус 1.
Это то, что в математике называется рекуррентным уравнением.
И мы можем написать это на Java в виде вызова функции power.
Если y равно 0, возвращаем 1.

Иначе, возвращаем x умножить на вызов этой же функции с x и y минус 1.
Таким образом, тот же метод, который мы определили с помощью цикла, может быть определен с помощью рекурсии.
Оба эти способа эквивалентны.
Но рекурсия позволяет записать сложное поведение простым способом, который потребует довольно сложного программирования при использовании циклов.
Рекурсию можно сравнить с матрешкой.

Чтобы понять это вернемся к рекурсивному методу, который мы определили.
И давайте упростим последовательно вызов этого метода для небольшой степени, чтобы увидеть, что происходит.
Начнем с x в 3 степени.
Мы можем заменить вызов метода, используя определение метода.

Таким образом, мы пишем весь код метода, подставляя вместо y 3.
И в этой последовательности выражений мы переходим от вызова метода с параметрами (x, 3) к вызову метода с параметрами (x, 2).
Пишем весь код метода, подставляя вместо y 2.

И в этой последовательности выражений, мы перешли от вызова метода с параметрами (x, 2) к вызову метода с параметрами (x, 1).
И переходим к вызову метода с параметрами (x, 0).

x в степени 0 равно 1.

Теперь нам нужно собрать все вместе.
power (x, 3) равно x умножить на power (x, 2).

А power (x, 2) равно x умножить на power (x, 1).
А power (x, 1) равна x умножить на power (x, 0), что равно 1.
Таким образом, мы получаем x умножить на x умножить на x умножить на 1.
Так работает рекурсия – сначала мы спускаемся как по лестнице вниз, а затем поднимаемся опять наверх.
Это изображение коробки с медсестрой, держащей меньшую коробку с тем же изображением.

Так что в теории, могут быть бесконечные медсестры и бесконечные коробки.
Но на практике нет бесконечных коробок, потому что изображение имеет некоторое разрешение, и мы не можем опуститься ниже 1 пикселя.
Таким образом, существует конечное число коробок.
Когда мы что-то вычисляем, мы должны заботиться о том, чтобы не создавать нежелательные бесконечные вычисления, которые нарушают нормальный поток вычислений.
Давайте посмотрим, что произойдет, когда мы что-то неправильно программируем.
Давайте рассмотрим, опять наш рекурсивный метод вычисления степени числа.
И давайте вызовем power (x, -2) для некоторого заданного x.

Для этого мы можем заменить вызов метода кодом.

В результате мы перейдем к вызову метода power (x, -3).
В методе power (x, -3) мы перейдем к вызову метода power (x, -4).

И так далее. Без конца.

Мы получим бесконечные вычисления в теории.
На практике мы получим переполнение в какой-то момент и ошибку.
Что же мы сделали не так?
В этом случае мы не соблюдали комментарий, что y должно быть больше или равно 0.
Поэтому мы должны учитывать две важные вещи.
Во-первых, рекурсия хороша, но мы можем перейти к бесконечным вычислениям.
И во-вторых, чтобы избежать этого, мы должны понять условия, при которых рекурсивный метод фактически завершается.
Может быть определенное количество рекурсивных вызовов, но в какой-то момент, нам нужно достичь не рекурсивного случая.
Поэтому при определении рекурсивного метода, всегда должны быть некоторые значения, для которых метод не вызывается рекурсивно.

Существует два способа чтения и понимания рекурсивных методов.
Один из них – это тот способ, который мы видели.
Другой, математический или нотационный способ, которые мы рассмотрим.
Предположим, нам дана задача написать рекурсивный метод.
Начнем с относительно простой задачи – написать метод на Java для вычисления факториала натурального числа.
В общем случае факториал натурального числа n вычисляется умножением всех натуральных чисел, начиная с 1 до n.
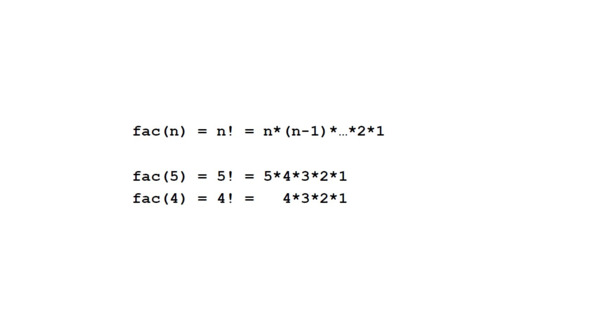
Чтобы решить эту задачу, мы будем использовать следующую стратегию.
Первая часть состоит в том, что мы предполагаем, что задача решена для более простой задачи того же рода.
Предположим, что нам нужно вычислить факториал натурального числа n, но мы уже знаем, как вычислить факториал n минус 1.
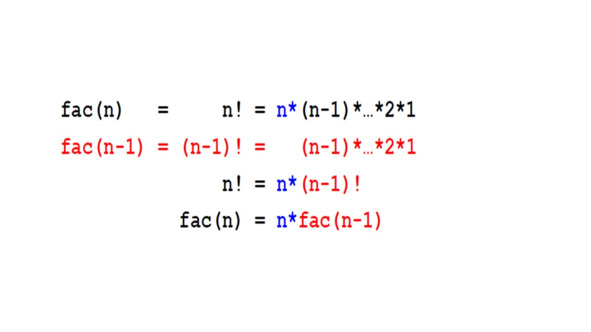
Если бы у нас был факториал n минус 1, мы просто бы умножили это число на n, чтобы получить факториал n.
Вторая часть стратегии – выявить случай, когда предыдущее рассуждение не выполняется.
Факториал 0 нельзя свести к более простому случаю, как мы это делали ранее.
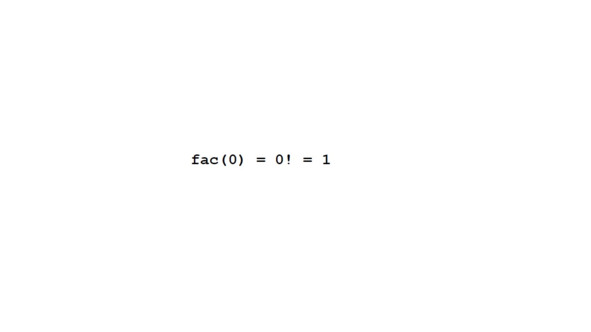
Так что это базовый случай.
Мы просто говорим, что факториал 0 равен 1.
Таким образом, факториал n равен 1, если n равно 0, и факториал n равен n умножить на факториал n минус 1, если n больше 0.
Теперь у нас есть основа для записи рекурсивного метода.
Из математического уравнения легко написать рекурсивный метод.

Там мы видим базовый случай, в котором нет рекурсивного вызова.
Базовый случай получается из пограничного случая.
И мы также видим рекурсивный случай, вытекающий из приведения общего случая к более простому.
Инкапсуляция. Объекты и классы

Давайте посмотрим на вычислительные возможности калькулятора.
Как правило, калькулятор может делать две вещи: запомнить значения и вычислить новые значения.

Запомнить значения можно с помощью переменных.
И затем мы можем вычислять новые значения с помощью методов.
Например, мы можем сложить два значения, вычесть или умножить.
Таким образом, у нас есть методы, соответствующие арифметике, а также методы, чтобы получить или установить переменную x.
Когда мы пишем программу для моделирования этого калькулятора, и мы определяем для него переменные и методы, мы поместим, с одной стороны, все переменные вместе, а с другой стороны – все методы вместе.
Значения всех переменных в конкретный момент времени будут составлять состояние калькулятора.
И набор методов будет определять поведение калькулятора.
Наша модель будет меняться от одного состояния в другое со временем.
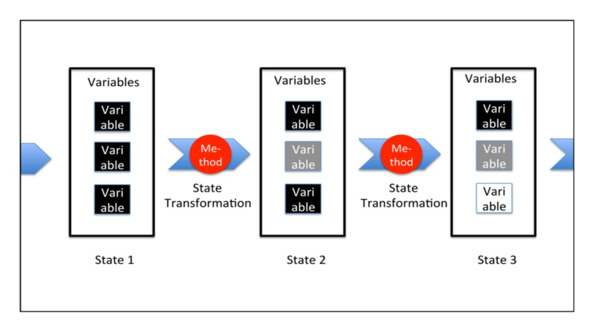
При этом состояние будет определяться значениями переменных.
А методы будут отвечать за изменение состояния.
На самом деле, определение переменных и методов – это общий способ моделирования объектов.
Эти объекты могут соответствовать физическим объектам, например, калькулятору.
Или эти объекты могут быть концептуальными, когда ваш код должен моделировать что-то новое.
Таким образом, это разделение состояния и поведения очень важно.
Представьте себе автомобиль, который моделируется в программе, которую вы пишете для игры.
Состоянием этого объекта может быть местоположение, цвет, включены ли фары или нет.
И методы могут быть изменением положения, включить свет фар и т. д.
Помните, что методы часто связаны с глаголами, потому что они подразумевают действие.
Теперь мы собираемся инкапсулировать переменные и методы в новую для нас конструкцию программирования, называемую объектом.
Эта концепция инкапсуляции является одной из ключевых концепций в так называемой объектно-ориентированной парадигме программирования.
Поэтому помните, что объекты имеют состояние, представленное отдельными переменными, которые также называются полями или атрибутами.
И поведение, то, что может делать наш объект, представлено методами.
Эти два компонента: состояние и поведение, не разбросаны по программе, а собраны и инкапсулированы в объекты.
Разные объекты могут иметь одинаковую структуру, и отличаться друг от друга только значениями переменных.
Поэтому мы можем сказать, что такие объекты принадлежат одному и тому же классу.
И наоборот, чтобы создать объект, сначала нам нужно сначала определить класс, который является шаблоном для создания объектов.
Рассмотрим пример с различными автомобилями, которые представлены различными объектами.
Все эти объекты принадлежат классу автомобилей Car, который имеет ряд атрибутов или переменных, или полей и ряд методов.
Давайте посмотрим на возможное определение, как мы можем записать этот класс на Java.

Здесь вы можете увидеть определение класса Car.
Вы можете увидеть зарезервированное ключевое слово class.
Затем имя, которое мы хотим дать классу.
Обратите внимание, что мы пишем его с заглавной буквы.
Затем мы указываем переменные с соответствующим типом.
Наконец, мы определяем методы, которые мы хотим дать всем объектам этого класса.
Но как только мы определили класс, как сконструировать объект для этого класса?
Для этого у нас есть конструкторы.
Конструкторы – это специальные методы, которые также включены в тело определения класса.

И они имеют имя класса.
Обратите внимание, что здесь не указан тип возвращаемого результата.
Используя конструкторы, мы можем создавать разные объекты класса.

Заметьте, что может быть не один, а несколько конструкторов.
Эти конструкторы отличаются списком параметров.
Здесь вы можете увидеть несколько возможных конструкторов для класса Car.
Также мы можем вообще не определять конструктор, и в этом случае при вызове конструктора объект создается со значениями по умолчанию.
Здесь мы видим несколько вызовов конструкторов, определенных ранее.
Посмотрите на объявление.
Сначала мы определяем объект с именем и обратите внимание, что классы работают как типы.
Сначала мы указываем Car, чтобы указать, что объект имеет тип или класс Car.
Затем знак равенства, зарезервированное ключевое слово new и вызов конструктора.
Таким образом, в итоге, чтобы определить объект, мы должны сначала определить класс, предоставляя набор полей и набор методов.

