65 ½ (не)детских вопросов о том, как устроено всё

Из второго закона Ньютона также следует, что чем тело тяжелее (чем больше его масса), тем сложнее будет его разогнать, или затормозить, или просто изменить траекторию его движения. Например, если вы приложите одну и ту же силу к лежащему на полу теннисному мячику и к тяжелому шару для боулинга, то они разгонятся по-разному, приобретут разные скорости. Равно как и в случае, если они летят вам навстречу, остановить теннисный мячик вам будет гораздо легче, на это потребуется гораздо меньшая сила.

Но как быть в случае, когда на тело действует не одна сила, а сразу несколько? Какую из них нужно подставлять в формулу второго закона Ньютона? Рассмотрим, к примеру, лежащую на столе книгу. На нее действует две силы: гравитация и сила реакции опоры (она же сила упругой деформации стола). Какая из этих сил определит ускорение книги? Оказывается, что обе. А точнее – их равнодействующая, т. е. векторная сумма всех действующих на книгу сил. А поскольку обе эти силы равны по величине и противоположны по направлению, то их равнодействующая равна нулю. Следовательно, никакого ускорения наша книга испытывать не будет, а будет продолжать лежать на столе, и мы сможем спокойно ее читать. Однако с чего мы взяли, что сила тяжести и сила реакции опоры равны? А это следует из третьего закона.

Третий закон Ньютона: два тела могут действовать друг на друга только силами, направленными вдоль одной прямой, причем эти силы равны по модулю и противоположны по направлению. Или в более простой и знакомой формулировке: сила действия равно силе противодействия. Это означает, что силы в природе всегда возникают парами: если тело А воздействует на тело Б некоторой силой, то в тот же самый момент тело Б подействует на тело А точно такой же силой, но направленной в противоположную сторону. Поэтому наша книга, которая давит на стол своим весом, заставляет этот стол сопротивляться этому давлению – так возникает сила реакции опоры. Вы можете и сами поэкспериментировать: надавите ладонью на стол, только не очень сильно. Что вы почувствуете? Стол будет сопротивляться и давить в ответ, но тоже не очень сильно. А если теперь увеличить силу давления? В ответ стол также увеличит силу своего сопротивления. Так что чем сильнее вы давите на стол, тем больше будет сила его реакции.

Но почему же тогда при падении, например, нашей книги на поверхность Земли ускоряется именно книга, а Земля не ускоряется? Ведь сила действия (сила притяжения книги Землей) должна быть равна силе противодействия (силе притяжения Земли книгой)? На самом деле ускоряется, просто мы этого не замечаем. И дело тут в массе этих двух тел. Поскольку масса Земли в миллиарды триллионов раз больше массы книги, то и ускорение, которое приобретает Земля, будет в миллиарды триллионов раз меньше ускорения книги, так что мы его вообще не сможем никак зафиксировать. А значит, можно говорить о том, что Земля в этом процессе остается неподвижной.

Вопрос 6. Что такое относительность?

На самом деле относительность придумал не Эйнштейн. Более того, долгое время он настаивал, чтобы его теорию называли не теорией относительности, а теорией инвариантности, поскольку в ее основе лежит принцип инвариантности (т. е. неизменности) всех физических законов при переходе из одной инерциальной системы отсчета в другую, а также в теорию вводится некоторая величина, инвариантная (т. е. не изменяющаяся) при таких переходах. Тем не менее идея относительности играет очень важную роль не только в теории Эйнштейна, о которой мы будем говорить в Части 5 (стр. 199), но и в классической механике. Поэтому давайте остановимся на этом понятии немного подробнее.

Представим, что вы сидите в кресле самолета. Перед вами на откидном столике лежит книга. Самолет летит со скоростью 800 км/ч. Вопрос: какая скорость будет у книги? Тут возможны, как минимум, два ответа. Во-первых, поскольку книга лежит прямо перед вами и никуда не движется, то ее скорость должна быть равна нулю. Во-вторых, поскольку эта книга находится вместе с вами в самолете, летящем со скоростью 800 км/ч, то и всё, что находится внутри самолета, также должно двигаться со скоростью 800 км/ч. Так какая же на самом деле у книги скорость: ноль или 800 км/ч? Ответ зависит от того, из какой системы отсчета мы за этой книгой наблюдаем. Если изнутри салона самолета, то скорость ее будет равна нулю; а если наблюдать за ней с земли – то 800 км/ч. Так что никакой скорости-самой-по-себе у книги нет, это величина относительная и в разных системах отсчета может принимать разные значения[3].

Давайте теперь спустимся с небес на землю и представим, что вы сидите в кресле современного поезда (достаточно современного, чтобы при его движении вы не ощущали никаких покачиваний). Если шторы на окнах будет плотно закрыты и не будет слышно стука колес, то будучи внутри вагона и не получая никаких сигналов извне (например, от GPS-навигатора) никакими экспериментами вы не сможете определить, движется ваш поезд или стоит на месте. Даже если скорость поезда будет 200 км/ч, абсолютно всё внутри вагона будет происходить так, как если бы он стоял на месте. В реальности мы понимаем, что поезд движется, только по стуку колес и небольшим колебаниям вагона (из-за неровностей рельс и неравномерного движения самого поезда). Если бы этих неровностей не было, то мы бы вообще не понимали, что происходит с нашим поездом.

Или другой пример. Наверняка вы хоть раз в жизни сталкивались с такой ситуацией: сидите вы в вагоне поезда, рядом с вами за окном стоит второй поезд так, что остальной пейзаж вам не виден. И вот вы замечаете, что поезд за окном начал двигаться. После чего несколько секунд вы не можете понять – то ли это ваш поезд поехал (и вы вместе с ним), то ли вы стоите на месте, а движется поезд за окном. И только посмотрев на другие объекты, находящиеся снаружи: на рельсы, землю, деревья – вы можете понять, кто на самом деле движется. Почему так происходит? Это точно не обман зрения и не оптическая иллюзия, а фундаментальный физический факт: состояние покоя и состояние равномерного прямолинейного движения неразличимы.

Действительно, все законы физики одинаковы и в вашем движущемся вагоне, и на поверхности Земли[4]. В этом суть принципа относительности. Его впервые сформулировал еще Галилей в своих «Беседах». Он заметил, что никакими опытами невозможно различить состояния покоя и равномерного прямолинейного движения (только в своих рассуждениях он использовал не вагон поезда, поскольку никаких поездов тогда еще не было, а трюм корабля):

«Уединитесь с кем-либо из друзей в просторное помещение под палубой какого-нибудь корабля, запаситесь мухами, бабочками и другими подобными мелкими летающими насекомыми; пусть будет у вас там также большой сосуд с водой и плавающими в нем маленькими рыбками; подвесьте, далее, наверху ведерко, из которого вода будет падать капля за каплей в другой сосуд с узким горлышком, подставленный внизу. Пока корабль стоит неподвижно, наблюдайте прилежно, как мелкие летающие животные с одной и той же скоростью движутся во все стороны помещения; рыбы, как вы увидите, будут плавать безразлично во всех направлениях; все падающие капли попадут в подставленный сосуд… Заставьте теперь корабль двигаться с любой скоростью – и тогда (если только движение будет равномерным и без качки в ту и другую сторону) во всех названных явлениях вы не обнаружите ни малейшего изменения и ни по одному из них не сможете установить, движется ли корабль или стоит неподвижно. Прыгая, вы переместитесь по полу на то же расстояние, что и раньше, и не будете делать больших прыжков в сторону кормы, чем в сторону носа, на том основании, что корабль быстро движется, хотя за то время, как вы будете в воздухе, пол под вами будет двигаться в сторону, противоположную вашему прыжку; … капли, как и ранее, будут падать в нижний сосуд, и ни одна не упадет ближе к корме, хотя, пока капля находится в воздухе, корабль пройдет много пядей»[5].

Конечно, скорость тела и траектория его движения сильно зависят от того, по отношению к какой системе отсчета рассматривается это движение. К примеру, капли внутри движущегося корабля будут падать вертикально вниз, а при наблюдении с земли мы увидим, что капли, помимо вертикального падения, также смещаются вперед вместе со всем кораблем. Тем не менее законы механики (те самые три закона Ньютона), описывающие это движение, остаются неизменными (инвариантными) во всех инерциальных системах отсчета. Нужно только преобразовать координаты из одной системы отсчета в другую. Этот принцип лежит в основе всей классической механики и называется принципом относительности Галилея. К нему также прилагаются правила преобразования, которые нужно выполнить при переходе из одной инерциальной системы отсчета в другую. Они также получили название преобразований Галилея.

Проиллюстрируем на примере, как работают преобразования Галилея. Если вы побежите со скоростью 10 км/ч навстречу поезду, который движется со скоростью 90 км/ч (в реальной жизни, конечно, лучше никогда так не делать), то вы будете сближаться со скоростью 90 + 10 = 100 (км/ч), т. е. ваши скорости будут просто складываться. А если вы осознаете всю опасность такого поведения, развернетесь на 180° и начнете убегать от поезда со скоростью 20 км/ч (хотя на самом деле лучше будет просто сойти с рельсов и пропустить этот поезд), то вы уже будете сближаться со скоростью 90–20 = 70 (км/ч), также в соответствии с преобразованиями Галилея.

Однако к концу XIX века обнаружилось, что такое правило сложения скоростей не работает в электродинамике. Из уравнений Максвелла следовало, что скорость всех электромагнитных волн (в том числе света) должна быть всегда одной и той же, независимо от того, в какой системе отсчета вы находитесь. Оказалось, что не важно, движетесь ли вы навстречу световой волне или, наоборот, удаляетесь от нее, вы всегда должны сближаться с одной и той же скоростью – со скоростью света. Это противоречие классической механики и электродинамики послужило толчком к созданию абсолютно новой физики, полностью перевернувшей наши представления о пространстве и времени, материи и энергии – теории относительности. Но об этом мы поговорим уже в Части 5, посвященной теории относительности (стр. 199).

Вопрос 7. Какие предметы быстрее падают: легкие или тяжелые?

Вопрос этот не так прост, как может показаться на первый взгляд. С одной стороны, наш повседневный опыт подсказывает, что тяжелые предметы падают быстрее. Действительно, все мы видели, как легкая пушинка или осенний листок долго и медленно падают на землю, в то время как наш собственный мобильный телефон, если его случайно выронить из рук, окажется на полу очень быстро. Почему так происходит? Первый ответ, который приходит в голову, – потому что Земля притягивает тяжелые предметы сильнее, а значит, они быстрее разгоняются. Однако и тут Галилей нашел что ответить. В своих «Диалогах» он предлагает немного об этом порассуждать.

Пусть мы выяснили, что мобильный телефон разгоняется быстрее, чем пушинка, поскольку он тяжелее. А что будет происходить, если мы привяжем их друг к другу и в таком виде отпустим в свободное падение? Возможны как минимум два способа рассуждения, приводящие к противоположным выводам:

1) Поскольку после того, как мы привязали пушинку к телефону, он стал тяжелее, то и разгоняться он должен теперь быстрее, чем раньше.

2) Поскольку пушинка разгоняется не так быстро, как телефон, то при падении в связке она будет его тормозить, так что разгоняться он теперь будет медленнее, чем раньше.

То есть из предположения, что тяжелые тела при падении разгоняются быстрее, чем легкие, мы получили логическое противоречие. Значит, исходное предположение неверно и все тела независимо от их массы должны разгоняться одинаково. Но почему же тогда телефон падает быстрее пушинки? Это же экспериментальный факт. Так происходит не из-за того, что масса телефона больше, чем у пушинки. А из-за силы сопротивления воздуха. Вес телефона значительно больше силы сопротивления, поэтому он разгоняется достаточно быстро. А вот вес легкой пушинки уже сравним с силой сопротивления, поэтому ее ускорение при падении не такое большое. Но если мы поместим пушинку и телефон в безвоздушное пространство и одновременно бросим, то они упадут также одновременно. И такие эксперименты проводились, причем не только на Земле.

2 августа 1971 года американский астронавт Дэвид Скотт во время миссии Аполлон‐15 (Apollo 15) провел этот эксперимент на поверхности Луны. В последний день экспедиции, когда команда уже собирала свою аппаратуру и упаковывала образцы лунного грунта, чтобы увезти все это на Землю, а миллионы зрителей по всему миру внимательно наблюдали за ними у экранов своих телеэкранов, командир корабля Дэвид Скотт вошел в кадр, держа в одной руке перо, а в другой – молоток, специально привезенные для этого с Земли. «Сейчас для вас мы проведем здесь эксперимент, – сказал он. – Я брошу эти два предмета, и, надеюсь, они упадут на поверхность одновременно». И что бы вы думали? Они действительно упали одновременно! Видеозапись этого эксперимента можно найти в Интернете, например, по запросу “молот и перо на луне”».

Чтобы убедиться в том, что воздух оказывает существенное влияние на скорость падения различных предметов, вы можете провести небольшой эксперимент даже у себя дома. Возьмите два одинаковых листа бумаги. Весят они одинаково, так что если бросить их одновременно, то и падать они будут примерно одинаково. А теперь скомкайте один из этих листов, чтобы из него получился маленький бумажный шарик, и повторите эксперимент. Вы увидите, что скомканный лист, несмотря на то, что его вес не изменился, будет падать значительно быстрее ровного листа бумаги. Так происходит потому, что сила сопротивления воздуха зависит от площади поверхности тела – чем она меньше, тем меньше будет сопротивление и тем быстрее тело будет разгоняться при падении.

Вопрос 8. Почему Луна не падает на Землю?

Мы с детства привыкли, что если подбросить какой-то предмет, то он обязательно упадет на землю. Даже если его изо всей силы швырнуть в небо, он всё равно через какое-то время упадет. И мы знаем, что это всё благодаря гравитации[6]– силе, которая притягивает к Земле все тела, находящиеся на ее поверхности. Это, кстати, еще одно открытие Ньютона – закон всемирного тяготения, который говорит о том, что все (вообще все) тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними:

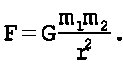
Здесь m1 и m2 – массы тел, r – расстояние между ними, а коэффициент G – фундаментальная постоянная гравитационного взаимодействия, одинаковая для всех тел во Вселенной.

Более простыми словами: чем более массивны тела, тем сильнее они притягиваются; и чем дальше они друг от друга – тем это притяжение будет слабее. Возможно, отсюда пошла поговорка «подобное притягивает подобное». Именно поэтому камень падает на Землю, а Луна не может улететь в космос и вынуждена вечно вращаться вокруг Земли.

Но почему же тогда Луна не падает на Землю, как падает камень? Как Луне удается преодолевать гравитацию? А дело тут в центростремительном ускорении. Давайте разберемся, что это такое, на совершенно другом примере, а также выясним, как можно преодолеть гравитацию. Возможно, вы когда-нибудь видели, как велосипедисты или мотоциклисты едут по потолку, т. е. делают мертвую петлю.

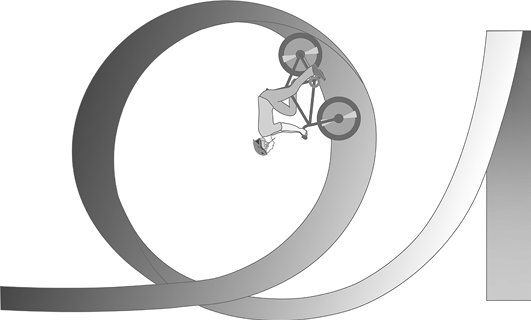
Почему, двигаясь вниз головой, велосипедист не падает? Как ему удается ехать по потолку? Дело в том, что его траектория не является прямой, он обязательно должен двигаться по окружности. Потому что при криволинейном движении тело каждую секунду изменяет направление своего движения (т. к. скорость всегда направлена по касательной к траектории), а значит – его скорость постоянно меняется. Не по величине, а по направлению. Но ведь это тоже изменение. А следовательно, тело испытывает ускорение. Оно и называется центростремительным, т. к. направлено вдоль радиуса в сторону центра окружности, по которой движется наше тело. Значит, по второму закону Ньютона, должна существовать соответствующая сила, отклоняющая его от прямолинейного движения. Это комбинация двух сил: гравитации и силы реакции опоры. Именно она постоянно меняет направление движения велосипедиста, удерживая его на круговой траектории. Величина этой силы зависит от скорости тела – чем больше скорость вращения, тем больше будет эта сила; а также от радиуса кривизны его траектории – чем меньше радиус, тем больше сила. Поэтому если велосипедист разогнался недостаточно, то его инерции не хватит, чтобы удержать его на потолке: гравитация окажется сильнее, и он рухнет на землю (так что не пытайтесь повторить этот опыт без присмотра квалифицированных физиков или родителей).

С подобным эффектом вы также можете встретиться в более безопасном эксперименте. Если привязать на веревку какой-то небольшой тяжелый предмет, например камень, и начать его вращать, то вы почувствуете что камень будет пытаться «улететь» от вас, все время растягивая веревку. Причем чем быстрее вы будете его вращать, тем большая сила потребуется, чтобы удержать его, тем больше будет сила натяжения веревки.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «Литрес».

Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Примечания

1

О том, почему эти силы равны между собой, мы поговорим в главе «В чем смысл трех законов Ньютона» (стр. 28).

2

Заметим, что в конструкции современных электронных весов используется другой принцип измерения силы. Основным элементом таких весов являются пьезоэлектрики. Это особые вещества, на поверхности которых под действием деформации индуцируется электрический заряд. По величине индуцированного заряда можно судить о величине приложенной силы, вызывающей эту деформацию.

3

Тут следует отметить, что в природе также существуют величины, не зависящие от системы отсчета. Например, величина электрического заряда будет одинаковой, независимо от того, из какой системы отсчета его измерять. Такие величины называются инвариантными.

4

Конечно, при условии, что поезд будет двигаться прямолинейно и с постоянной скоростью (т. е. без ускорения). Такие системы отсчета называются инерциальными.

5

5 Галилео Галилей. Диалог о двух главнейших системах мира. Москва-Ленинград: ОГИЗ – СССР, 1948. 380 с.

6

Хотя в ХХ веке выяснилось, что с гравитацией не всё так просто, и что это вообще никакая не сила. Но об этом мы поговорим в Части 5, посвященной общей теории относительности (стр. 199).