Теория безмассовой материи

Необходимо сформировать расчетные кластеры изначальной воды по аналогии с рисунком 7. Для этого кластер (2) надо умножить на 1,618 и получить кластер (3). Кластер (3) умножить на 1,618 и получить кластер (4) и т. д. На рисунке 9 изображена масштабная модель расчетных кластеров изначальной воды.

Теперь в исходной начальной точке физического кластера (2), да и всех остальных расчетных кластеров, приложим вращательное усилие, моделируя воздействие массового объекта на изначальную воду. В результате получим водоворот кластеров воды с условными границами, определяемыми расчетными кластерами. Данный водоворот изображен на рисунке 10. Кластеры вращаются своего рода как эксцентрик вокруг своего центра масс вращения, с одной стороны кластера линейная скорость быстрее с другой медленнее. Потому что центр масс расчетного кластера (центр вращения) смещен. Одна сторона кластера больше другой на 1,618. Поэтому при вращении самого кластера создается засасывающее усилие по направлению к стороне с большей линейной скоростью, т.е. к меньшей стороне кластера. В это же время на противоположной стороне кластера создается усилие, которое пытается компенсировать засасывающее усилие. При этом, чем ближе кластеры к общему центру масс, тем меньше сам расчетный кластер. К примеру, отталкивающее усилие в кластере 7 меньше, чем засасывающее усилие в кластере 6, а в кластере 6 меньше, чем в 5 и т. д. Потому что, чем ближе кластер к общему центру масс вращения, тем быстрее он вращается вокруг своего эксцентрика и вокруг общего центра масс. Таким образом, в результате формируется усилие по притяжению кластеров к общему центру масс по графику функции, построенном по числам золотого сечения (рис. 10 справа).

Теперь можно представить, что кластеры, входящие в круг с радиусом равным кластеру (2) вращаются всех быстрее, вокруг центра масс приложенного усилия. Затем чуть медленнее вращаются расчетные кластеры (3), которые располагаются в круге радиусом от центра масс до размера кластера (3) (который в свою очередь отличается от предыдущего кластера на 1,618) и т. д. Всех медленнее вращается кластер (7), в котором содержаться все физические кластеры вращающегося объема изначальной воды, отнесенные к плоскости вращения. При этом сами физические кластеры ближе к общему центру масс не приближаются и не удаляются, но при этом создают засасывающее усилие по направлению к общему центру масс. Своего рода кластеры как по эстафете от дальнего к ближнему передают усилие по притяжению к центру масс водоворота.

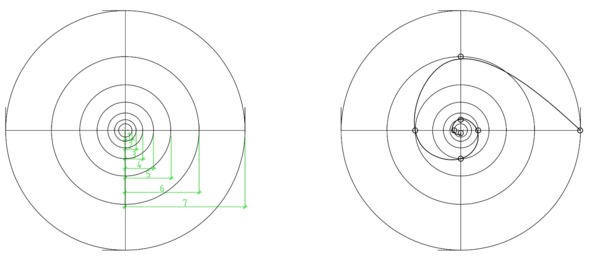
Рисунок 10

На рисунке 10 правый график показывает каким образом будет меняться усилие по притяжению физического кластера (2) изначальной воды в зависимости от расстояния до центра масс вращения. Правый график на рисунке 10 построен по числам золотого сечения. Конечно, в связи с тем, что физические кластеры изначальной воды с одинаковой силой притягиваются и отталкиваются друг от друга и все время находятся на одинаковом минимальном расстоянии друг от друга, кластеры изначальной воды физически не будут перемещаться по указанной траектории. В зависимости от расстояния до центра масс водоворота физические кластеры будут вращаться с определенной скоростью, не отдаляясь и не приближаясь к центру масс. Но чем ближе к центру масс, тем быстрее вращаются физические кластеры вокруг центра масс, достигая своего апогея в окружности в центре масс с радиусом в один физический кластер. Поэтому график отображает изменение усилия для физического кластера по притяжению к центру масс в зависимости от расстояния до центра масс.

Давайте рассчитаем какое усилие будут испытывать физические кластеры изначальной воды в зависимости от расстояния до центра масс водоворота, вызванного массовым объектом.

Силу, приложенную к кластерам изначальной воды в виде направленного завихрения можно определить по формуле:

F=m*a (1)

где,

m – масса совокупности физических кластеров изначальной воды, подвергающиеся воздействию усилия;

а – центростремительное ускорение физических кластеров изначальной воды, подвергающиеся воздействию усилия.

То есть сила, с которой кластеры изначальной воды взаимодействуют с массовым объектом, равна силе, с которой массовый объект воздействует на изначальную воду. Вода, своего рода, возвращает объекту его возмущающее действие.

Рассмотрим, как изначальная вода формирует усилие в направлении центра масс своего вращения. В центре масс содержится массовый объект, который создает воздействие на изначальную воду.

На рисунке 11 показан массовый объект в виде черной точки, вокруг которого сформировано два расчетных кластера изначальной воды. При этом первый расчетный кластер будет являться также и физическим. Расчетные кластеры показывают, как измениться центростремительное ускорение изначальной воды при условии, что расчетный кластер, находящийся ближе к центру масс обладает энергией меньше на 1,618, чем последующий соединенный с ним кластер.

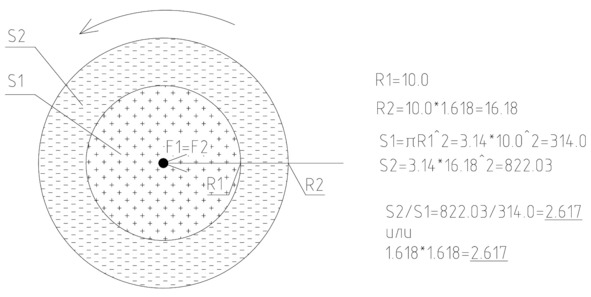
Рисунок 11

Вокруг массового объекта формируется «водоворот» изначальной воды. При этом, чем дальше от центра водоворота, тем меньше центростремительное ускорение для кластеров изначальной воды. Для наглядности представим, что размер ближайшего кластера к центру масс равен 10 (R1=10). Второй кластер будет больше первого на 1,618. Соответственно, размер второго кластера будет 10*1,618 = 16,18 (R2 = 16,18).

То есть в радиусе R1 будет располагаться определенное количество кластеров изначальной воды, массу которых можно охарактеризовать через площадь круга с радиусом R1. При этом массу кластеров, находящихся в радиусе R2 можно охарактеризовать через площадь круга с радиусом R2.

Получаем:

S1=π*R1^2=3,14* (10) ^2=314,0

S1=π*R2^2=3,14* (16,18) ^2=822,03

Соотношение между большим и меньшим кругами составит:

S2/S1 =822,03/314,0=2,617

При этом квадрат числа золотого сечения 1,618 составит 1,618*1,618= 2,617.

То есть для изначальной воды, состоящей из представленных расчетных кластеров, каждый следующий последовательно отстоящий от центра масс расчетный кластер в данной плоскости вращения будет обладать массой, большей в 2,617 раза предыдущего кластера.

Это условие можно представить на физическом уровне следующим образом. Представим водоворот обычной воды, вызванный быстрым вращением массового объекта в центре некоего объема воды. Молекулы воды непосредственно у массового объекта будут вращаться с максимальной линейной скоростью и обладать максимальным центростремительным ускорением. Чем дальше от центра водоворота, тем молекулы воды перемещаются медленнее. У них уменьшается линейная скорость и центростремительное ускорение. Но они в любом случае будут вращаться вокруг массового объекта, потому что молекулы воды сцеплены между собой. Но чем дальше от центра, тем медленнее они будут вращаться, потому что хоть усилие ко всем молекулам некоего объема воды передается одинаковое, но масса общего количества молекул воды возрастает.

Чем к большей массе молекул воды приложено усилие, тем медленнее они вращаются.

Вернемся к конструкции на рисунке 11. Запишем, усилия с которыми кластеры изначальной воды действуют на центр масс:

F1=m1*a1

F2=m2*a2

При этом F1=F2. Но усилие F1 формируют кластеры в радиусе R1, а усилие F2 кластеры, находящиеся в радиусе R2.

Таким образом,

m1*a1=m2*a2 (2)

При этом, зная, что массы двух соседних кластеров находятся в соотношении 1,618^2 = 2.617, можно записать,

m2= (1,618) ^2*m1 (3)

Теперь, преобразовывая уравнение (2) получим,

m1*a1= (1,618) ^2*m1*a2

a2= (m1*a1) / ((1,618) ^2*m1)

или

a2=a1/ (1,618) ^2

Получившееся соотношение центростремительных ускорений двух соседних расчетных кластеров изначальной воды является частным случаем, когда рассматриваются два последовательно расположенных кластера.

Давайте выведем общее уравнение связывающее изменение центростремительного ускорения и расстояние кластеров до центра масс.

Для этого рассмотрим пример на рисунке 12.

Представим, что на изначальную воду воздействует массовый объект. Он создает водоворот в изначальной воде. При этом известно, что для кластеров изначальной воды находящихся на расстоянии в 6400 км от центра масс водоворота центростремительное ускорение составляет 9,8 м/с2. Необходимо определить значение центростремительного ускорения для кластеров изначальной воды находящихся на расстоянии 42500 км от центра масс водоворота, вызванного массовым объектом.

Для начала необходимо задаться размером «исходного» расчетного кластера изначальной воды. Примем, что исходный расчетный кластер будет равен 6400 км.

Сколько «исходных» расчетных кластеров изначальной воды будет содержаться в искомом размере «конечного» расчетного кластера, размер которого равен 42500 км?

Зная, что каждый последующий расчетный кластер содержит в себе предыдущий и больше его в 1,618 раза, количество «исходных» расчетных кластеров, содержащихся в «конечном» расчетном кластере можно рассчитать по формуле:

R1*1,618*n=R2

где, n – коэффициент масштабирования.

Тогда

n=R2/ (1,618*R1)

Ранее в уравнении (3) было показано, что массы соседних расчетных кластеров соотносятся как квадрат числа золотого сечения 1,618. При этом больший кластер в соседних кластерах содержит в себе только один кластер. Поэтому для частного случая соседних кластеров n = 1. В общем виде уравнение (2) можно привести к виду:

a2=a1/ (1,618*n) ^2 (4)

В соответствии с уравнением (4) можно рассчитать центростремительное ускорение для физических кластеров изначальной воды, находящихся на любых расстояниях от центра масс водоворота. Для этого необходимо знать центростремительное ускорения для физических кластеров на одном определенном расстоянии от центра масс.

Теперь используя полученные уравнения рассчитаем центростремительное ускорения для примера на рисунке 12.

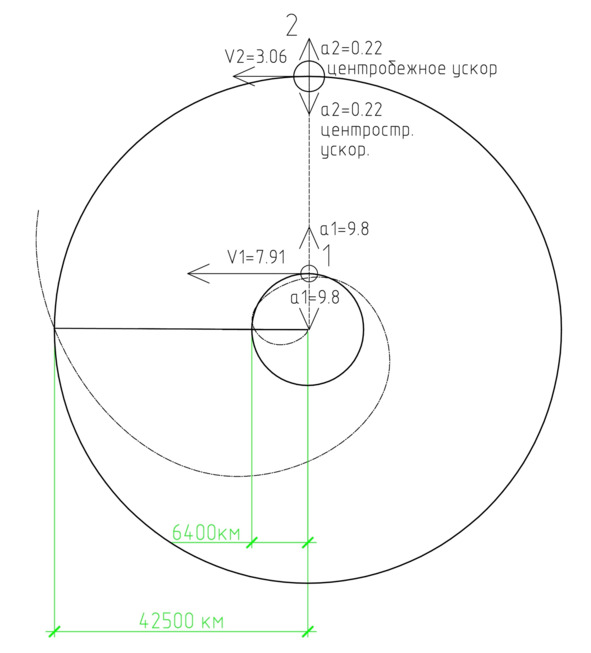
Рисунок 12

R1 = 6400 км, R2 = 42500 км,

a1 = 9,8 м/с2,

тогда,

n=R2/ (1,618*R1) =42500/ (1,618*6400) =4,1

a2=a1/ (1,618*n) ^2 =9,8/ (1,618*4,1) ^2 =0,22 м⁄с^2 =0,22* (10) ^ (-3) км⁄с^2

Зная центростремительное ускорение физических кластеров изначальной воды, вращающейся вокруг центра масс массового объекта на расстоянии 42500 км определим линейную скорость данных кластеров.

Центростремительное ускорение в классической физике определяется как

a=V^2/R

тогда

V=√ (a*R).

Тогда для нашего примера,

V2=√ (a2*R2)

V2=√ (0.22*42500* (10) ^ (-3)) =3,06 км⁄с

Данные для примера на рисунке 12 взяты не случайно. Массовый объект создающий возмущение в изначальной воде (водоворот) это Земля. Ускорение свободного падения у поверхности Земли 9,8 м/с2. При этом расстояние от центра масс Земли около 6400 км. На расстоянии от центра масс Земли в 42500 км находится геостационарная орбита. Скорость спутников на этой орбите составляет 3,06 км/с.

Напрашивается следующий вывод: Возможно, что данные спутники просто дрейфуют в круговом течении в кластерах изначальной воды, которые вращаются вокруг центра масс массового объекта с определенной скоростью, зависящей от расстояния и от массы объекта, создающего гравитационное возмущение.

Действительно, сила, с которой кластеры притягиваются к центру масс водоворота одинакова с силой, с которой массовый объект воздействует на изначальную воду. То есть на рис. 12 центростремительное ускорение, воздействующее на спутники, дрейфующие в потоке изначальной воды на соответствующих орбитах, равно центробежному ускорению для того же спутника. Поэтому спутник движется по круговой орбите в потоке изначальной воды со скоростью перемещения кластеров изначальной воды на данном расстоянии от центра масс. Если скорость спутника станет меньше, то соответственно вырастит значение центростремительного ускорения, а значение центробежного ускорения станет меньше. Поэтому сила притяжения к центру масс станет больше, чем сила отталкивания, и спутник начнет приближаться к центру масс, при этом увеличивая свою скорость. Если скорость спутника будет больше чем скорость потока изначальной воды, то значение центробежного ускорения станет больше, чем центростремительного и спутник начнет отдаляться от центра масс.

Отталкиваясь от такого вывода становится понятна природа космических скоростей.

Первая космическая скорость позволяет начать вращаться вокруг Земли.

V_1=√ (a_1*R_1) =√ (9.8*6400* (10) ^ (-3)) =7.91 км⁄с

Спутники на околоземной орбите просто дрейфуют в круговом течении физических кластеров изначальной воды. Если спутник затормозить, то он начнет перемещаться ближе к центру масс массового объекта, создающего водоворот. При этом кластеры изначальной воды начнут разгонять спутник, потому что, чем ближе спутник к центру масс, тем быстрее вращается изначальная вода. Если спутник начать разгонять искусственно, то чем дальше он будет отдаляться от центра масс, тем меньше будет становится скорость вращения изначальной воды, что будет приводит к торможению спутника. Но выйдя из водоворота Земли спутник попадет в водоворот Солнца. Хотя и Земля, и спутник всё время находятся в водовороте Солнца, но на определенном масштабе водоворот Земли является для спутника определяющим его перемещение в изначальной воде.

К примеру, массовые объекты на поверхности земли также находятся в потоке кластеров изначальной воды, но данные объекты имеют незначительную линейную скорость по отношению к скорости проходящих через них кластерам изначальной воды, поэтому притягиваются к центру масс Земли практически напрямую. Данные объекты не могут дрейфовать со скоростью потока кластеров, потому что находятся на земле. Человек своего рода испытывает нагрузку в виде прохождения через него кластеров изначальной воды. При этом кластеры, за счет ускорения, которое они передают по направлению к центру масс Земли, затягивают любые массовые объекты на поверхности земли в центр масс водоворота. За счет этого воздействия у человека формируется скелетно-мышечный аппарат.

Используя данную методику расчета изменения центростремительного ускорения были произведены расчеты для планет солнечной системы. Результаты расчетов представлены в таблице 1.

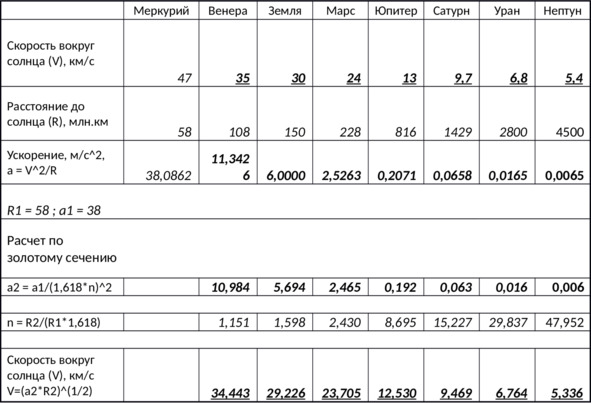
Таблица 1

В верхней части таблицы представлены общеизвестные данные по средней скорости вращения планет по орбите вокруг Солнца и по расстоянию до Солнца. Затем производится расчет центростремительного ускорения каждой планеты по отношению к центру масс водоворота, создаваемого Солнцем. После этого в качестве «исходного» расчетного кластера принимается кластер размером с радиус усредненной орбиты Меркурия (R1=58 млн. км), при этом центростремительное ускорение для Меркурия составляет a1=38 м/с2.

Затем производится расчет центростремительных ускорений и линейных скоростей для всех представленных планет.

К примеру, для Земли, при условии, что R2 = 150 млн. км.

n=R2/ ((R1*1,618)) =150/ ((58*1,618)) =1,6

a2=a1/ (1,618*n) ^2 =38/ (1,618*1,6) ^2 =5,7

V2=√ (a2*R2) =√ (5,7*150) =29,24 км⁄с

Для Юпитера,

n=816/ ((58*1,618)) =8,69

a2=38/ (1,618*8,69) ^2 =0,192

V2=√ (0,192*816) =12,5 км⁄с

Таким образом для всех планет были получены данные по центростремительному ускорению и линейной скорости через золотое сечение кластеров изначальной воды. Как можно видеть из таблицы 1 реальные значения этих параметров фактически соответствуют расчетным через метод золотого сечения.

Очевидно, что можно произвести расчет центростремительного ускорения и линейной скорости вращения физических кластеров изначальной воды вокруг центра масс массивного объекта задаваясь любым размером «исходного» расчетного кластера.

К примеру, в качестве размера «исходного» расчетного кластера можно взять расстояние от Земли до Солнца. Тогда R1=150 млн. км, a1=6,0 м/с2.

Для Меркурия получаем,

n=58/ ((150*1,618)) =0,2389

a2=6/ (1,618*0,2389) ^2 =40,15

V2=√ (40,15*58) =48,2 км⁄с

Для Сатурна

n=1429/ ((150*1.618)) =5,887

a2=6/ (1,618*5,887) ^2 =0,066

V2=√ (0,066*1429) =9,72 км⁄с

Расчеты через «исходный» кластер для Земли представлены в таблице 2

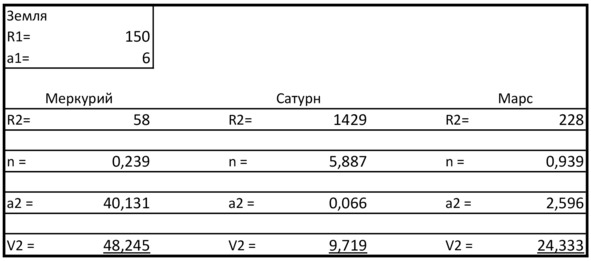
Таблица 2

Как можно видеть из таблицы 2 немного различаются только значения для Меркурия (линейная скорость по расчету золотого сечения больше на 48,24—47=1,24 км/с). Остальные значения можно отнести к расчетной погрешности.

Далее произведем расчет центростремительного ускорения кластеров изначальной воды, находящихся на расстоянии Луны от центра масс Земли. Результаты расчета представлены в таблице 3.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «Литрес».

Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.