
Полная версия:
Искусство выбора: комбинаторика успеха и творчества

Ирина Поддубская
Искусство выбора: комбинаторика успеха и творчества
Введение
Выбор из множества вариантов является неотъемлемой частью человеческой жизни. Мы сталкиваемся с ним ежедневно от самых простых решений, таких как выбор одежды или того, что приготовить на ужин, до сложнейших, влияющих на судьбу: выбор места учебы или работы, будущего для наших детей. Иллюстрации к русским сказкам и былинам на тему выбора правильного пути на развилке перед Вещим камнем с надписью «Направо пойдешь – коня потеряешь…», как нельзя лучше отражают мысль о том, что каждое решение несет в себе вероятность как успеха, так и потерь. Каждый наш выбор – это, по сути, комбинаторная задача: чтобы сделать правильный выбор, важно не упустить ни один из возможных вариантов. Перечислением и подсчетом занимается специальный раздел математики – комбинаторика.
В современном мире востребованы цифровые профессии, связанные с компьютерными системами, в области анализа данных, кибербезопасности и т.д. За ними будущее. Преимущество будут иметь те выпускники, которые получили хорошее математическое образование, то есть умеющие переводить разного рода задачи на математический язык. И комбинаторика как раз подходит для развития этих навыков.
Однако знание комбинаторных принципов необходимо не только в науке и технике.
Благодаря своей широкой практической направленности, комбинаторика представляет особый интерес для изучения. Автор книги, учитель математики средней школы, преподаватель курса «Математика. Вероятность и статистика», однажды поставил себе задачу привлечения внимания обучающихся к эффективности использования возможностей математики в повседневной жизни.
При этом, автор понимал, что сухая подача фактов в виде истории развития комбинаторики от мистического соединения символов в древности до современного анализа ДНК может не заинтересовать большую часть учащихся поколения Z («зумеры» – люди, родившиеся в промежутке с 1997 по 2012 годы), для которых Интернет с рождения был частью сознательной жизни. Зумеры и сами умеют находить любую информацию, чувствуют себя комфортно в мире технологий, воспринимая прогресс, как должное, они сами создают новые идеи по решению глобальных проблем. Они живут в мире мгновенной связи, где все визуально, мыслят мемами и рилсами и самовыражаются через социальные медиа. Tik-Tok используют не только в развлекательных, но и образовательных целях.
В то же время зумеры отличаются повышенной внимательностью к своему психологическому здоровью, отстаивают свое право на баланс между работой и личной жизнью. Зумеры лучше воспримут информацию в виде ярких трендов, которые, к тому же, позволяют упростить жизнь. Потому что еще одной тенденцией у зумеров становится стремление к минимализму, облегчению жизни и работы и избавлению от всего, что их усложняет.
Автор предложил при изучении комбинаторного правила умножения обучающимися использовать примеры из их личной жизни, популярные тренды, такие как правильное питание, капсульный гардероб, создание мемов, а также интерактивные приемы решения практических задач, имеющих связь с развитием полезных для жизни навыков или с будущей самореализацией учащихся. Такими примерами могут быть сервисы-конструкторы: Foodplan, Getwardrobe, Storyboard That и т.д.
Шаг за шагом, находя для обучающихся всё новые примеры практического применения комбинаторики в жизни, автор пришел к идее создания книги. Цель книги – не только популярно объяснить всем желающим комбинаторные принципы в простых вещах. Автор видит своей миссией привлечь внимание к красоте и гармонии математической науки в целом. Математикой пропитана вся наша жизнь. Одним из главных элементов которой является искусство выбора. И каждому нашему поступку, определяющему будущую судьбу, предшествует внутренняя работа, схожая с комбинаторным анализом.
Автор обращает внимание читателей на важную составляющую книги. Это продолжение национальной идеи. У нас были, есть и будут свои яркие представители, герои, просто добрые люди, способные оказать влияние на развитие культуры и общества в целом, на знания и опыт которых мы можем полагаться. Таким представителем может стать каждый из будущих выпускников.
I. Комбинаторика как наука
Комбинаторика – раздел математики, занимающийся перечислением и подсчетом комбинаций элементов разных множеств. Основными методами перечисления и упорядочивания множеств элементов в комбинаторике, которые изучают в школе, являются правило умножения, перестановки и сочетания.
1. Основные понятия комбинаторики
Правило умножения.
Если первый элемент в комбинации можно выбрать m способами, а второй – k способами, то общее количество комбинаций из двух элементов равно m*k. В продолжение: если третий и так далее элемент можно выбрать n3, n4 и т.д. способами, то общее количество способов организовать упорядоченные множества этих элементов будет рассчитываться, как произведение количества элементов в этих множествах. Школьная задача в этом случае может состоять в том, сколькими способами можно составить пару ведущих из мальчиков и девочек, учащихся в одном классе.
Перестановки – комбинации, которые образуются из различных предметов при расположении их в ряд на различных местах, меняя всеми возможными способами:
Если есть n предметов, то число способов их пронумеровать (число перестановок) равно n! – факториалу числа, равного количеству этих предметов. Например, сколькими способами можно составить расписание уроков или очередь к врачу.
Сочетания – наборы элементов, взятых из множества. Сочетания показывают, сколькими способами можно выбрать k элементов из n элементов. Например, сколькими способами можно выбрать 3 цветка в букет, если имеется 8 видов цветков.
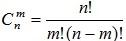
В математике комбинаторные правила применяются в теории вероятности, статистике и их приложениях, когда необходимо перечислить все возможные исходы с помощью специальных методов. В то же время комбинаторика не является абстрактной наукой, она служит универсальным инструментом для других наук и демонстрирует свою эффективность в различных областях человеческой деятельности: экономика, домохозяйство, спорт и хобби.
Историю комбинаторики можно рассматривать в двух ключах.
Как раздел науки, комбинаторика появилась довольно поздно, благодаря вниманию исследователей к азартным играм, которые, в свою очередь, имеют гораздо более древнюю историю.
В то же время комбинаторные принципы пронизывают всю нашу жизнь и находят применение не только в абстрактных математических задачах. Поэтому человек всегда стремился замечать и использовать их на протяжении всей истории развития общества. Попытки людей понять и систематизировать мироздание с помощью математических инструментов являются одним из способов добавить предсказуемости в жизни человека.
2. Комбинаторика: случайность или осознанный выбор
С доисторических времен люди стояли перед необходимостью расположения охотников во время охоты, воинов во время битвы с противником. Затем во время физических подготовок появились состязания и игры на выносливость в беге, прыжках, поднятии тяжестей, стрельбе из орудий и бросании предметов. На сегодняшний день в спорте нашла применение статистическая система оценки вклада каждого конкретного игрока и его влияние на результат всей команды. На помощь приходит компьютерное моделирование. Комбинаторные принципы в спорте играют важную роль в выборе эффективных стратегий и тактик в зависимости от количества игроков, их позиций на поле и набора игровых действий.
В определенный момент времени зародились игры с соперником, в которых надо было просчитать его планы и избежать проигрыша. Нарды, шашки, шахматы и их национальные вариации в основе своей предусматривают различные сочетания передвижения фигур и вычисление наиболее выигрышной комбинации ходов. В свою очередь, компьютерные шахматы появились, благодаря созданию математической модели шахматной игры.
Несмотря на то, что игра в кости (кубики с нанесенными на них очками) также считается древней, математические исследования с их помощью долго не заслуживали внимание ученых. Первыми заметили закономерности заядлые игроки, которые и пытались разобраться, составляя таблицы для подсчета сочетаний очков, чтобы получить определенную сумму. Но, в конечном счете, именно на кубиках и монетах были доказаны первые теоремы комбинаторики и теории вероятности. Многие важные факты были получены в экспериментах с игральными кубиками и монетами.
Более того, теория вероятности и комбинаторика, как раздел математики, долгое время развивались, как вычисление шанса на победу и выигрышных игровых комбинаций. А еще монета часто помогает людям в ситуации выбора, когда они решают доверить свою судьбу воле случая. Например, судья подбрасывает монетку, чтобы определить какая команда вступает в игру первой.
В истории музыки есть неоднозначный пример сочетания случайности и выбора: изобретение игры с целью времяпровождения и развлечения на светских мероприятиях, в которой для составления новой музыкальной композиции использовался обычный игральный кубик и нумерованная таблица тактов. Об этом подробнее в главе «Комбинаторика и музыка».
Кубик Рубика также является изобретением и наглядным пособием по комбинаторике.
Разработчики компьютерных игр и интерактивных программ используют алгоритмы, базирующиеся на принципах комбинаторики, для создания большого количества уникальных игровых уровней, подбора комбинаций предметов и навыков, генерации случайных событий и выбора стратегии, для создания персонажей и их расстановки в игровом мире. С одной стороны, в этом суть оптимизации программы и алгоритмов игры, с другой стороны, комбинаторика позволяет обеспечить разнообразие и баланс в игре, гарантируя пользователю интересные правила игры и сюжет, то есть служит пространством для творчества.
Здесь и далее будут рассматриваются обе составляющие практического применения комбинаторики в различных сферах жизнедеятельности человека: комбинаторика, как, собственно, алгоритм оптимизации множества элементов, и, как творческий процесс, искусство выбора из возможных вариантов.
Искусство выбора служит не только источником творчества, но и отражением желания действовать, исходящее изнутри. Бросок кости или монеты в ситуации выбора – как метафора, объединяющая силу случайности и выбора. Выбор взрослого человека – это не просто случайный бросок игрального кубика, а осознанный процесс, включающий анализ и учет всех «за» и «против» при принятии решения.
Комбинаторика, очевидно, имеет широкую практическую направленность, тому демонстрацией и подтверждением являются примеры, бережно собранные автором в этой книге.
III. Комбинаторика в деятельности человека
Будущие выпускники школ стоят перед одним из самых важных выборов в своей жизни – выбором профессии. Этот выбор часто оказывается сложным и многогранным, требующим анализа множества факторов, от личных предпочтений до перспектив рынка труда. Многие даже не задумываются о том, что математическая дисциплина, такая как комбинаторика, играет значительную роль в эффективном решении многих проблем, с которыми сталкиваются специалисты самых разных профессий. Комбинаторика, наука о подсчете и перечислении комбинаций, оказывается незаменимым инструментом в решении задач оптимизации, планирования и анализа больших объемов данных. В каких же профессиях знание комбинаторики необходимо, а порой и критически важно?
1. Комбинаторика в разных профессиях
Производство. Комбинаторные принципы используются в любом производственном процессе для оптимизации конфигурации изделий, планирования объемов выпуска и управления запасами. Например, производство машин: автомобиль состоит из тысяч деталей, каждая из которых может иметь несколько вариантов исполнения (цвет, материал, производитель и т.д.).
Управление запасами. Это тоже своего рода комбинаторная задача, учитывая ограниченные условия хранения.
Транспорт и логистика. При планировании маршрутов доставки товаров комбинаторное правило умножения используется для оценки общего количества возможных путей, позволяя оптимизировать маршруты и минимизировать затраты времени и топлива. Это особенно важно для больших логистических сетей.
Задача оптимизации расписания полетов, учитывая множество ограничений, таких как количество самолетов, экипажей, аэропортов и времени, также решается с помощью комбинаторных алгоритмов.
Маркетинг. При разработке нового продукта компании часто проводят маркетинговые исследования, тестируя различные комбинации дизайна, цены и рекламной кампании, чтобы выбрать наиболее эффективный вариант.
Финансовый рынок. В инвестиционном анализе комбинаторные правила применяются при оценке вероятности разных сценариев развития рынка, чтобы определить оптимальную инвестиционную стратегию. Возможность комбинировать различные активы и инструменты увеличивает число комбинаций, а правило умножения помогает системно их оценить. В сфере страхования оцениваются риски и выплаты, моделируются вероятностные процессы.
Защита информации, криптография. Безопасность данных – в современном мире первостепенная задача. Поиск уязвимостей в системах безопасности часто сводится к перебору различных комбинаций действий и поиска наиболее эффективных способов взлома. Надежный пароль должен быть сложным и уникальным. Предположим, что пароль должен состоять из 8 символов, которые могут быть любыми буквами английского алфавита (26 букв) или цифрами от 0 до 9 (10 цифр). Тогда общее количество возможных паролей будет равно (26 + 10) в 8ой степени ≈ 2,8 * 10 в 12ой степени – это астрономическое число, которое делает подбор пароля методом перебора практически невозможным. Добавление еще одной цифры увеличивает количество кодов еще в 36 раз. Этот принцип лежит в основе многих систем кодирования, используемых в компьютерах и других устройствах.
Управление персоналом и проектами, планирование учебного процесса. При формировании команд, не только в спорте, но и в бизнесе, комбинаторные правила помогают оценить число возможных сочетаний сотрудников с различными навыками и опытом, и распределить ресурсы между участниками проекта, что важно для достижения максимальной эффективности работы.
Социология и анализ данных. Комбинаторные методы позволяют предсказывать демографические тренды, моделировать распространение заболеваний. Анализ связей между пользователями в социальных сетях, выявление влиятельных пользователей, рекомендательные системы, прогнозирование распространения информации, позволяют бизнесу эффективно таргетировать рекламные компании, а исследователям – понимать динамику социальных взаимодействий. Анализ трафика на веб-сайте или предсказание поведения покупателей также требует поиска закономерностей и выявление скрытых связей.
Математика, как наука и как дисциплина в школе, само собой разумеется, использует для решения различных задач подсчет комбинаций, перестановок и размещений. С помощью этих методов оценивается вероятность, проверяются гипотезы и строятся статистические модели.
Химия, биология. Комбинаторное правило используется для подсчета числа возможных конформаций молекул, что важно для понимания их свойств и функций,
В химии – для подбора оптимальных параметров реакции и выбор наилучших катализаторов.
В биоинформатике – для подсчета числа возможных последовательностей нуклеотидов или аминокислот, для анализа биологических данных, построения геномов, моделирования биологических процессов и поиска лекарств
В биологии комбинаторное правило умножения играет ключевую роль в понимании генетической изменчивости. Гены, как строительные блоки организма, комбинируются, создавая огромное разнообразие генотипов и фенотипов. Число возможных генетических комбинаций определяется числом аллелей (вариантов гена) для каждого гена и числом генов. Анализ геномных данных, поиск генов и предсказание белковой структуры – это задачи, где комбинаторика играет важную роль.
Фармацевт подбирает оптимальные составы препаратов, а врач – оптимальную схему лечения.
Создание электронных устройств. При проектировании микросхем комбинаторное правило умножения позволяет оценить сложность задачи и количество возможных комбинаций элементов схемы и их расположения для обеспечения максимальной производительности и минимального энергопотребления.
Дизайн интерьеров с выбором цветовых комбинаций, декоративных элементов, способов расстановки мебели для создания гармоничного пространства.
Выбор подарка и организация event-мероприятий, планирование путешествий.
Планирование меню для создания разнообразных и полезных блюд.
Составление гардероба для оптимизации шоппинга и рационального использования вещей.
Профориентация для выбора карьеры на основе комбинации различных факторов, индивидуальных способностей и личных интересов.
В действительности, многие профессии требуют умения анализировать варианты, оценивать вероятности и находить оптимальные решения. И всё это напрямую связано с комбинаторными методами. Таким образом, комбинаторика – не просто абстрактная математическая дисциплина. Она способствует пониманию окружающего мира и находит широкое применение в самых различных областях человеческой деятельности. Практически в любой сфере, где присутствует множественность выбора, правило умножения является незаменимым инструментом эффективного, обоснованного выбора и безопасного, взвешенного решения задач, связанных с подсчетом вариантов, планированием и оптимизацией процессов. Поэтому понимание алгоритмов комбинаторики представляет собой важный навык, полезный, как в профессиональной деятельности, так и в повседневной жизни.
В следующих главах вы найдете практикоориентированные примеры использования комбинаторики в обычной жизни – выборе одежды и того, что приготовить.
2. Комбинаторика и «наука» о стиле
«Хороший вкус – это как математика на уровне второго класса школы. Научиться одеваться стильно, со вкусом, статусно, уместно – легко, если рядом с вами профессиональный и любящий преподаватель». Татьяна Тимофеева, стилист, основательница Школы шоппинга.
«Forbes» (рус. «Форбс»), известный финансово-экономический журнал, чьи рейтинги и оценки успешных проектов в экономике и бизнесе имеют авторитет во всем мире, назвал Татьяну русской Керри Бредшоу. А журнал Marie Claire назвал ее лучшей женщиной-предпринимателем после владелицы Wildberries. Она ведет блог о стиле, обучает стилистов, ее клиентами являются успешные и знаменитые люди из списка Forbes.
Татьяна Тимофеева – яркий пример того, как человек, ценящий красоту и гармонию, любящий свою профессию, смог систематизировать науку о стиле и в настоящий момент помогает другим подбирать и сочетать подходящие им вещи в идеальный гардероб.
Классический женский гардероб «Нечего надеть и некуда вешать». По мнению, Татьяны, создание гардероба – это игра, которая может приносить удовольствие и пользу. Одним из принципов современного гардероба является создание базовой капсулы. Базовая капсула – это набор простых и универсальных вещей, которые хорошо сочетаются друг с другом, легко комбинируются между собой, всегда остаются в моде и закрывают потребности нескольких сфер жизни. Цель создания капсульного гардероба – упростить жизнь и сэкономить время и деньги, кроме того, снижается уровень стресса по поводу того, как выглядеть.
Если из элементов капсулы складываются разные образы, в зависимости от их сочетания, то принципы комбинаторики здесь имеют прямое практическое применение. В качестве примера, возьмем тренд по созданию капсульного гардероба, ставшего популярным, благодаря блогерам TikTok. Метод «3/3/3» утверждает, что на сезон для полноценного гардероба достаточно иметь 3 верха, 3 низа и 3 пары обуви. Давайте попробуем подсчитать:
Каждый верхний элемент одежды можно взять один из 3, нижний – также один из трех, обуви – 1 из 3. Получается множество вариантов для верхней части одежды состоит из 3 элементов, для нижней – также 3 элемента, и для обуви можно взять один из 3 вариантов. По правилу умножения, множество упорядоченных пар состоит из n*k элементов. Количество возможных вариантов пар одежды из 3 элементов верха и 3 элементов низа составит: 3х3=9. Если каждую пару дополнять одним из трех вариантов обуви, то получится уже 9х3=27 комплектов. Если же добавить несколько аксессуаров, в этом случае возможности создания новых образов увеличиваются по тому же правилу.
На первый взгляд, этот комбинаторный прием в создании гардероба ориентирован исключительно на женскую аудиторию. Однако, вы удивитесь, узнав, что, пожалуй, самое раннее практическое подтверждение связи раздела математики, комбинаторики, и работы стилиста приводит ученик средней школы, подготовивший еще в 2015 году проект, направленный на профориентацию и показывающий взаимосвязь математических знаний и творческой профессии.
Комбинаторика позволяет вычислить все возможные комбинации в одежде. При этом важно понимать и другие принципы гармоничного стильного образа, такие как: цветовые сочетания, особенности фигуры, формы и так далее.
Особое значение приобретает перебор вариантов и комбинаций в творческом смысле. Не зря для этого будет достаточно примеров в этой книге из абсолютно разных сфер жизни человека. Это огромный источник для вдохновения, в том числе и в моде. Примером тому служит работа дизайнеров одежды, которые выбирали в своей профессии направление для поиска творческих идей в комбинации форм, материалов и рисунков. В специализированной литературе есть описание комбинаторных экспериментов известного модельера Джанни Версаче в послевоенные годы, когда люди стали предпочитать индивидуальному пошиву покупку одежды массового производства в магазинах широкого потребления. Модельер непрерывно изучал историю одежды разных времен и народов, книги по искусству, архитектурные сооружения, природные пейзажи, а затем соединял их в своих эскизах.
Задачу выбрать и расположить рисунки, узоры, украшения в одежде люди решали еще с древности. По мере развития общества и качества отношений, когда все большее значение приобретают взаимодействия между людьми для построения деловых контактов, личной жизни, развивалось и искусство выглядеть эстетично и гармонично. Не на последнем месте в современном обществе стоит и уверенность в себе, устойчивая самооценка. В этом помогает наука о стиле, одним из полезных инструментов которой смело можно назвать комбинаторный принцип. Этот прием позволяет экономить основные ресурсы современного человека: время, деньги и нервные клетки, и, кроме того, служит источником для творчества.
Примерами интерактивного решения задачи создания гардероба для женщин и мужчин, которые помогают скомбинировать вещи и создать образы в одежде, являются такие популярные приложения, как Getwardrobe, Stylebook, Smart Closet, Outfit Maker и т.д. Вместо специальных приложений можно использовать графические сервисы и самостоятельно организовать комбинации вещей: PowerPoint, Paint, Canva, фотоколлаж. Некоторые торговые площадки предлагают собственные онлайн-сервисы (онлайн-капсулы), которые после небольшого опроса подберут вам образы из одежды подходящего фасона, цвета, стиля.
3. Комбинаторика и наука «Меню-менеджмента»
Составление меню – одна из сфер, демонстрирующих практическое применения комбинаторных приемов в повседневной жизни.
Приготовление блюд – это не высшая математика, но дается не всем. Сложности здесь аналогичны проблеме идеального гардероба («Нечего надеть – некуда повесить»): вроде бы купишь кучу всего, а поесть нечего.
Наука «Меню-менеджмента» обучает ценным знаниям, как собрать продукты в полноценные, разнообразные и полезные блюда, сэкономив при этом время, силы, деньги. Ощущение спокойствия без суеты, организованности без усталости обещает автор системы, популярный фуд-блогер Дарья Черненко, автор тренингов и книг, которая уже много лет помогает женщинам решать главную задачу: чтобы в доме всегда была еда вкусная и полезная и это отнимало минимум ресурсов.
Изначально автор предлагала помощь по составлению меню, в том числе с помощью конструкторов блюд. Представьте, что все ингредиенты любого салата можно представить в виде определенной комбинации продуктов относящихся к определенному типу: белковое, зеленое и овощное, хрустящее, соленое или сладкое, приправа и заправка. Значит можно создать удобный конструктор, с помощью которого можно создавать многообразие комбинаций. Для этого необходимо из каждой группы продуктов взять по одному любому ингредиенту и заправить заправкой по вкусу. Например, если в вашем холодильнике есть любые 3 белковых продукта (мясо, птица, яйца), капуста и горошек (2), морковь и огурцы (2), любой фрукт (1), чеснок и петрушка (2), майонез, сметана, соевый соус, растительное масло (4), то вы сможете скомбинировать и приготовить салат

