
Полная версия:
Как ломаются спагетти и другие задачи по физике

Игорь Иванов
Как ломаются спагетти и другие задачи по физике
Редактор Антон Никольский
Издатель П. Подкосов
Руководитель проекта И. Серёгина
Ассистент редакции М. Короченская
Корректоры О. Петрова, С. Чупахина
Компьютерная верстка А. Грених
Макет и дизайн обложки Ю. Буга
Иллюстратор К. Панфёрова
Задачи, вошедшие в сборник, были опубликованы на сайте «Элементы» (elementy.ru). Издательство благодарит редакцию сайта за активное участие в подготовке сборника к изданию и Фонд развития теоретической физики и математики «Базис» – за предоставление прав на публикацию задач.
Фонд «Базис» основан в 2016 году. Миссия Фонда – системная поддержка и развитие фундаментальной науки, прежде всего физики и математики, в России, поддержка и повышение уровня образования в этих областях, содействие международному научному сотрудничеству российских ученых, повышение интереса молодежи к науке.
© Фонд развития теоретической физики и математики «БАЗИС», 2022
© Иванов И., 2022
© ООО «Альпина нон-фикшн», 2022
Все права защищены. Данная электронная книга предназначена исключительно для частного использования в личных (некоммерческих) целях. Электронная книга, ее части, фрагменты и элементы, включая текст, изображения и иное, не подлежат копированию и любому другому использованию без разрешения правообладателя. В частности, запрещено такое использование, в результате которого электронная книга, ее часть, фрагмент или элемент станут доступными ограниченному или неопределенному кругу лиц, в том числе посредством сети интернет, независимо от того, будет предоставляться доступ за плату или безвозмездно.
Копирование, воспроизведение и иное использование электронной книги, ее частей, фрагментов и элементов, выходящее за пределы частного использования в личных (некоммерческих) целях, без согласия правообладателя является незаконным и влечет уголовную, административную и гражданскую ответственность.
* * *СЕРИЯ «НАУЧНО-ПОПУЛЯРНЫЕ ЗАДАЧИ»

Вот уже больше десяти лет каждую неделю на сайте «Элементы» выходит новая задача – по физике, математике, лингвистике, биологии, химии или даже по астрономии, экономике, археологии. В понедельник публикуется условие, в среду – одна или несколько подсказок, в пятницу – решение и научно-популярное послесловие. Эту структуру мы оставили и в книге, прибегнув к небольшим хитростям, чтобы подсказка и решение не попались вам на глаза раньше времени.
Ради послесловия – рассказа о том, как затронутые в задаче вопросы решаются в науке и в жизни, – и был придуман этот жанр. Послесловие превращает задачу в научно-популярную статью – и уже не так важно, удалось ли вам ее решить, вы получите удовольствие в любом случае.
Серию открывают сборники задач по физике и лингвистике. Готовятся к выходу математика и биология. А на elementy.ru/problems вас всегда ждет свежая задача.
Увлекательного вам чтения!
Редакция «Элементов»Благодарности
Для меня было огромным удовольствием работать над этой книгой вместе с командой великолепных специалистов: редактором Джейн Эванс и выпускающим редактором Ханной Снетсингер из издательства Jessica Kingsley Publishers, иллюстраторами Дженнифер Уитни (картинки к упражнениям для самопомощи) и Амандой Уэй (оформление цитат в конце каждой главы), благодаря которым эта работа стала такой яркой и замечательной. Я благодарю мужа, детей, маму, брата и золовку, которые дарили мне любовь и поддержку, и кошку, которая постоянно топталась на моем ноутбуке. Большое спасибо подруге и наставнику Эрзе Уэрб за то, что направляла меня на протяжении всей работы над книгой. Спасибо Эрике Кертис, Мэгги Линч, Майку Сонксену, Стивону Льюису, Эндрю Лоустону и Иден Бирн за их безграничный оптимизм. Спасибо прекрасным клиентам и студентам, с которыми мне посчастливилось встретиться. Все разработанные мной приемы самопомощи они испытывали на себе, делились наблюдениями и помогали определить, что из этого реально работает. Спасибо подписчикам в Instagram (@risawilliamstherapy), которые читали мои советы, а также Кэтрин Килти из Breathe Magazine и Шиван Чхве, которые публиковали мои статьи по психологии. Отдельное спасибо Тит Нат Ханю, Джозефу Кэмпбеллу, Марисе Пир, Джен Синсеро, Эстер Хикс, Брене Браун, Экхарту Толле, Мари Кондо, Мартину Селигману, Дэвиду Бернсу, Уэйну Дайеру и Виктору Франклу за их вдохновляющие книги. Я благодарю судьбу за то, что они оказали такое влияние на мою жизнь, и надеюсь, моя работа тоже привнесет в мир немного добра и света.
Предисловие
В средних классах школы во мне странным образом уживались два разных отношения к физике. Школьную физику я учил более-менее хорошо, на твердую четверочку, но никакого воодушевления она у меня не вызывала. Грузики на наклонной плоскости, пружинки жесткости k, сообщающиеся сосуды, провода с током… Даже если иногда приходилось решать задачи «со звездочкой», задачи повышенной трудности, это были все те же грузики и пружинки, только более запутанные. Зато дома я зачитывался литературой по элементарным частицам, черным дырам, космосу и термоядерному синтезу. Вот это реальная физика, настоящая, восхитительная – ожившая научная фантастика! А школьная физика – так, пыль.
Затем была новосибирская физматшкола с ее уникальными, совершенно нескучными курсами физики. Шикарные лекции по физике нам читал Михаил Алексеевич Могилевский, а параллельно шли факультативные курсы по физике полупроводников, квантовой механике, элементарным частицам. И я, тогдашний школьник, с удивлением осознал, что некоторые вопросы из современной физики я способен постигать количественно, через решение задач, специально адаптированных для продвинутых школьников. Конечно, до настоящей исследовательской науки было еще очень далеко. Но тот разрыв между школьной и современной физикой, который раньше ощущался как безбрежная и бездонная пропасть, вдруг стал обозримым.
Методы и закономерности современной физики перестают казаться таинственными чудесами, если сам способен сосчитать что-то оттуда, пусть даже совсем элементарное и с подсказками. Я уверен, что любой человек, интересующийся современной физикой, пусть и без специального физического образования, имеет право и возможность совершить этот прыжок. Искренне надеюсь, что собранные в этой книжке задачи помогут вам испытать интеллектуальное удовольствие.
Перед вами – задачи не повышенной трудности, а повышенной интересности. Они не натренируют вас на сдачу ЕГЭ или на решение олимпиадных задач. Они подарят удовольствие от более тесного знакомства с окружающей физической реальностью, позволят вам «пощупать руками» современную физику. Некоторые из них очень простые, другие посложнее, отдельные задачи – трудные; уровень задач отмечен звездочками. Но все их объединяет одно: они опираются на школьный багаж знаний, дополненный иногда научно-популярными материалами, и при этом так или иначе касаются реальных научных исследований.
Типы заданий тут самые разные. Есть задачи вычислительные: они, хоть и выглядят технически как школьные задачки, по сути представляют собой упрощенный анализ какой-то реальной ситуации из современной физики. Есть также целый класс задач-оценок. В них не требуется получить точный ответ; более того, какого-то единственного, абсолютно правильного ответа может и не оказаться. В них надо лишь найти главные зависимости между величинами – и именно это будет считаться решением задачи, что, между прочим, в современной физике встречается сплошь и рядом. Наконец, есть задачи на «подумать», в которых вообще не требуется что-то вычислять. Вся суть таких задач – разобраться с явлением и получить удовлетворяющий вас самих ответ.
Каждая задача – миниатюра, выстроенная вокруг одного физического вопроса. Задача начинается со вступления, которое обрисовывает тему, дает нужные сведения и, постепенно подводя вас к проблеме, завершается формулировкой вопроса. Затем следуют подсказки разной степени детализации. Потом – авторское решение, которое не всегда является единственно верным путем к ответу. И завершает сюжет послесловие: в нем тема развивается чуть дальше и приводятся ссылки на реальные исследования и публикации.
Тематическая группировка задач довольно условна. Скажем, в задачах из блока «Механика» встречаются и элементарные частицы, и гравитационные волны. Но и что из того? Это не учебник и не задачник для контроля усвоенного материала. Тут не скажешь: «Мы этого не проходили!» Это, скорее, ваш «туристический путеводитель» по избранным тропам современной физики – и то, как вы пройдете по каждой тропе, зависит от вашего любопытства и готовности преодолевать сложности. Конечно, задачи можно просто читать одну за другой, не затрудняя себя их решением, – и я надеюсь, что даже в таком режиме книжка окажется очень полезной. Но вы получите куда более полное впечатление, если все же остановитесь на несколько минут и попробуете самостоятельно справиться с задачей – а потом задержитесь еще раз, прочитав подсказки. В конце концов, и настоящее путешествие запоминается куда ярче, если вы весь маршрут проделаете пешком, а не промчитесь в автомобиле.
Так что – в путь, и удачи и удовольствий вам!
Игорь ИвановМеханика
1. Оптимизируйте коллайдер

Большой адронный коллайдер (БАК) – самый сложный научный прибор, построенный человеком. В нем протоны, разгоняясь до очень больших энергий, врезаются друг в друга, в результате чего рождаются новые необычные частицы, разлетающиеся в разные стороны из точек столкновений. Многометровые детекторы, словно гигантские микроскопы, разглядывают этот процесс: регистрируют частицы, измеряют их свойства и по ним восстанавливают картину соударений. Через такие столкновения мы и выясняем, из чего состоит и как функционирует Вселенная на самом мельчайшем масштабе. Мы задаем природе четко поставленные вопросы, и она, не в силах отвертеться, выдает свои фундаментальные секреты один за другим.
И хотя это, безусловно, самая передовая физика, мы начинаем книгу с задачи про коллайдер! И она будет вам по силам – потому что даже в сложнейших процессах встречаются очень простые явления. Признаемся по секрету: для решения этой задачи не требуется даже знание законов физики, поможет самая обыкновенная смекалка.
ЗадачаНо давайте сначала познакомимся с устройством коллайдера. На рис. 1 очень схематично изображено основное кольцо БАК. Реальное его устройство, конечно, сложнее, но для этой задачи мы намеренно упрощаем ситуацию. По кольцу навстречу друг другу циркулируют протонные пучки. На самом деле они летают в двух близких вакуумных трубах, но для простоты будем считать, что все происходит в одной трубе. Каждый пучок состоит из отдельных компактных облачков (сгустков) протонов.
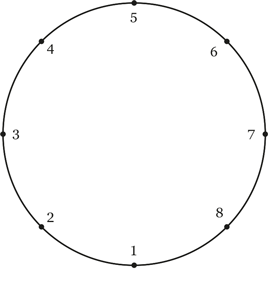
Рис. 1. Схема коллайдерного кольца с восемью точками пересечения встречных пучков
Будем считать, что в восьми точках вдоль кольца, расположенных на одинаковом расстоянии друг от друга, траектории встречных пучков пересекаются, и там протоны могут сталкиваться друг с другом – если, конечно, сгустки пролетят сквозь эту область одновременно! Впрочем, даже если сгустки пересеклись, то это вовсе не значит, что все протоны из одного облачка столкнулись с протонами из другого. Они очень разреженные, так что подавляющее большинство протонов ни с кем не сталкивается, соударения испытывают только несколько протонов из многих миллиардов. Поэтому сгустки в целом просто проходят друг сквозь друга, продолжая лететь по своей траектории, и готовы встречаться на каждом обороте снова и снова.
А теперь представьте себе, что вы сидите в пультовой коллайдера и управляете запуском пучков в ускорительное кольцо. Вы можете послать в него несколько сгустков, причем не обязательно поровну в обоих направлениях. Считается, что все сгустки летят с одинаковой скоростью, но то, как именно они будут размещены на кольце, зависит только от вас! Ваша задача – сделать так, чтобы столкновения происходили во всех восьми точках.
Выясните, какое минимальное число сгустков надо запустить в кольцо коллайдера и как именно их расположить относительно друг друга, чтобы этого добиться.
Подсказка
Пожалуй, единственное, что можно здесь сказать, – эту задачу вполне решают обыкновенные школьники средних классов.
РешениеПервым делом подмечаем, что любая встречная пара сгустков, движущихся с одинаковой скоростью, будет встречаться на кольце ровно два раза в диаметрально противоположных точках. Если мы хотим задействовать таким образом восемь точек, то минимальное количество встречных пар – четыре.
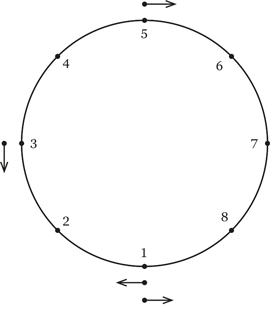
Рис. 2. Оптимальная последовательность сгустков в кольце
Четыре встречные пары можно организовать двумя способами. Первый вариант: один сгусток в одну сторону, а четыре – в другую; всего пять сгустков. Второй вариант: в обе стороны летят по два сгустка – всего четыре. Значит, второй вариант более оптимальный.
Осталось подобрать взаимное расположение сгустков так, чтобы все четыре попарных комбинации встречались в указанных местах. Пример такого расположения показан на рис. 2. Это и есть решение задачи.
ПослесловиеУ решения есть одна неожиданная особенность: оно менее симметрично, чем постановка задачи. Никакого глубокого вывода отсюда не следует, но, как показывает опыт, бывает так, что эта несимметричность становится препятствием при поиске ответа: мозг подсознательно ожидает, что решение будет столь же симметричным, как и условие.
Любопытно, что и в реальности, на самых первых этапах запуска и отладки БАК применялась примерно такая схема. В настоящем кольце этого коллайдера столкновения происходят не в восьми, а в четырех точках (с номерами 1, 2, 5, 8), вокруг которых построены крупные детекторы ATLAS, ALICE, CMS и LHCb. Но расположены они все равно в вершинах правильного восьмиугольника. Благодаря этому при запуске коллайдера можно было проверить работоспособность всех детекторов с минимальным количеством сгустков в пучках. А уже затем, когда техники убедились в стабильности пучков и надежности аппаратуры, они начали планомерно повышать интенсивность. В пике интенсивности в каждом пучке циркулируют более 2000 сгустков. Они следуют друг за другом с интервалом 25 наносекунд, то есть на расстоянии примерно восемь метров друг от друга, и заполняют практически все кольцо. Но подчеркнем, что даже при такой плотной загрузке столкновения происходят только в тех четырех местах, где две вакуумные трубы пересекаются.
Дополнительная информация
Подробную информацию на русском языке об устройстве и научных задачах Большого адронного коллайдера, а также связанную с ним ленту новостей можно найти в специальном проекте на сайте «Элементы»: elementy.ru/LHC.
БАК – крупнейший, но далеко не единственный научный проект ЦЕРНа, Европейской организации ядерных исследований. О других научных исследованиях, технических разработках и образовательных мероприятиях ЦЕРНа можно узнать на его сайте: home.cern.
2. Хоккейная задача

В прошлой задаче мы сразу нырнули в самую современную физику. А теперь давайте вынырнем и обратимся к повседневной жизни, поговорим о спорте. Спорт – это движение, а значит, в нем тоже можно углядеть интересные и подчас неожиданные физические явления. Возьмем, например, хоккей. При кистевом броске хоккеисты часто закручивают шайбу, так что она одновременно скользит по льду и вращается. Если движение шайбы не ограничивать размерами хоккейной коробки, то рано или поздно и вращение, и скольжение остановятся из-за трения о лед. Но что прекратится раньше?
Этот вопрос может удивить: неужели тут есть какие-то общие закономерности?! Да, есть, и мы сейчас их разберем.
ЗадачаРассмотрим слегка упрощенную задачу. Пусть вместо шайбы у нас будет однородное узкое и плоское кольцо. Его запускают скользить по горизонтальной поверхности, придав некоторую начальную скорость и некоторое вращение (рис. 1). Между кольцом и поверхностью действует обычное сухое трение: сила трения пропорциональна прижимающей силе, не зависит от модуля скорости проскальзывания и направлена в противоположную от скорости сторону.
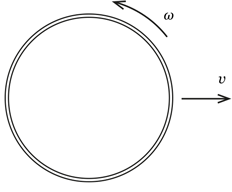
Рис. 1. Вращающееся тонкое кольцо скользит по горизонтальной поверхности (вид сверху)
Выясните, что остановится раньше – скольжение или вращение кольца.
Подсказка
Задача может показаться неприступной из-за того, что в условии практически ничего не задано. Нет ни размеров колечка, ни начальных скоростей скольжения и вращения, ни коэффициента трения. На самом деле, когда задача формулируется таким образом, это обычно служит намеком на то, что ответ не будет зависеть от конкретных параметров. Поэтому при решении вы сами можете взять какие-то значения для этих величин, но должны проследить, что они действительно исчезнут из ответа.
Кольцо участвует сразу в двух движениях: скользит и вращается. Из-за векторного сложения поступательного и вращательного движения разные части кольца движутся относительно поверхности в разные стороны (нарисуйте колечко, представьте, как оно движется, и убедитесь, что разные участки действительно в данный момент скользят по поверхности в разных направлениях). Поэтому выберите вначале какой-то маленький участок на кольце и сосчитайте силу трения, действующую именно на это место. Подумайте, как влияет эта сила на вращательное и поступательное движение, и попытайтесь усреднить эти два влияния по всему кольцу.
После этого проанализируйте формулы для трех случаев: когда скорости вращения и движения совпадают, а также когда скорость вращения очень мала или, наоборот, очень велика по сравнению с поступательным движением. Это наведет вас на мысль, как ответить на вопрос задачи.
РешениеРассмотрим участок кольца, который находится под углом α к направлению движения (рис. 2). Пусть в данный момент времени скорость центра масс кольца равна v, а скорость вращения обода u = ωR, где ω – угловая скорость вращения в данный момент, а R – радиус кольца. Этот кусочек кольца участвует в поступательном и вращательном движении. Его скорость относительно поверхности показана на рисунке серой стрелкой. Она составляет угол β с направлением поступательного движения, причем
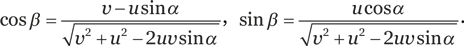
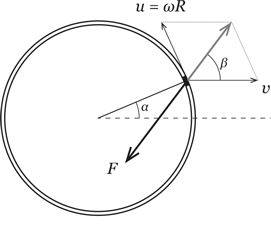
Рис. 2. Скорости и силы на маленьком участке кольца
Эти выражения выглядят громоздкими, но они получаются из обычных формул сложения двух векторов скоростей.
Сила трения, действующая на этот участок, по модулю равна F = μmg (здесь m – масса участка кольца) и направлена в противоположную от скорости сторону. У этой силы есть проекция на направление поступательного движения, – F cos β, и проекция на касательную к кольцу, которая притормаживает вращение, – F sin (β – α). Не стесняясь, подставим сюда выражения для синуса и косинуса угла β, а также учтем, что sin (β – α) = sin β cos α – cos β sin α:
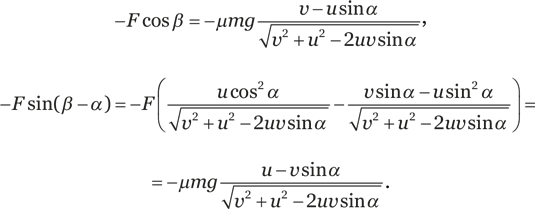
У этой силы есть также проекция вбок, то есть перпендикулярно поступательному движению, но при усреднении по всему кольцу эта проекция обнулится. В этом можно убедиться математически, если рассмотреть второй участок, находящийся под углом π – α. Для него построение аналогичное, две притормаживающие проекции будут такими же, а сила вбок – ровно противоположная.
Для того чтобы посчитать эффект для всего кольца в целом, надо сложить эти силы по всему кольцу, то есть учесть элементы кольца, расположенные под всеми углами α. Это даст нам два ускорения, притормаживающих поступательное движение и вращение:
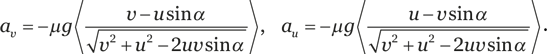
Угловые скобки обозначают усреднение по всем углам α; это последствие того, что мы общую силу поделили на общую массу. При желании его можно выразить через интегралы, но это не обязательно.
Заметьте интересную особенность полученных формул: при замене u на v выражения для au и av превращаются друг в друга. Такая «дуальность» задачи автоматически означает, что если бы начальные скорости u и v были равны, то ускорения au и av тоже были бы одинаковые и, значит, соотношение u = v выполнялось бы всегда, до самой остановки. А это, в свою очередь, означает, что вращение и скольжение в данном случае прекратятся одновременно. Смотрите, произошло математическое «чудо»: мы, просто глядя на формулы, вдруг получили ответ для нашей задачи, по крайней мере для одного начального состояния!
А что изменится, если начальные скорости u и v различаются? Тогда ускорения тоже будут отличаться, и, казалось бы, заранее не понятно, что будет замедляться быстрее. Чтобы выяснить, может ли при этом вращение остановиться раньше скольжения, рассмотрим ситуацию, когда скорость вращения u много меньше скорости поступательного движения v. Тогда для поступательного ускорения мы получим примерно av = −μg, словно вращения и не было. Для вращательного ускорения au получим маленькую величину порядка −μg·u/v, поскольку «большой» вклад, пропорциональный синусу, обнулился после усреднения по всем углам (более точное выражение см. в послесловии). Иными словами, если вращение очень медленное, то оно и замедляется намного медленнее, чем скольжение. Можно сказать и так: относительное замедление вращения (au/u) пропорционально относительному замедлению скольжения (av/v). Отсюда и следует, что скольжение и вращение не могут прекратиться в разные моменты времени.
Выше мы отметили, что задача математически симметрична относительно замены поступательного движения на вращательное. Поэтому мы совершенно аналогичным способом получаем и второй вывод: если поступательное движение намного медленнее вращения, то и замедляться оно будет намного медленнее вращения. Соответственно, и в этом случае нет никакой возможности остановить скольжение раньше вращения.
Итак, ответ: вращательное и поступательное движение прекратятся одновременно вне зависимости от того, каковы были их начальные скорости.
ПослесловиеАнализ формул можно немного продолжить. Когда u много меньше v, усреднение надо произвести более аккуратно, разложив знаменатель дроби в ряд по малому параметру u/v. Ответ для ускорения вращения окажется вдвое меньше той оценки, которую мы привели в ходе решения. Эти два ускорения можно поделить друг на друга и получить простое выражение:
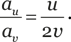
Коэффициент 1/2 имеет вполне осязаемые последствия. Он меньше единицы, и отсюда получается, что отношение u/v, пусть поначалу очень маленькое, будет увеличиваться с течением времени. А поскольку задача математически симметрична относительно замены поступательного движения на вращательное, отсюда можно заключить, что если отношение u/v очень велико, то с течением времени оно будет уменьшаться. Мы приходим к простому выводу: какими бы ни были начальные скорости u и v, в процессе движения они будут не только синхронно уменьшаться (это мы уже установили в ходе решения), но и все больше приближаться друг к другу.
Для тех, кто знаком с дифференциальными уравнениями, отметим, что нечувствительность ответа к конкретному соотношению между начальными скоростями вращения и скольжения имеет простое математическое объяснение: уравнение для отношения u/v имеет «устойчивую неподвижную точку» при u/v = 1. Это значит, что, каким бы ни было начальное значение u/v, за счет взаимного влияния вращения и скольжения система сама стремится к этому значению в ходе эволюции во времени.

