Репетитор по математике. Алгебра

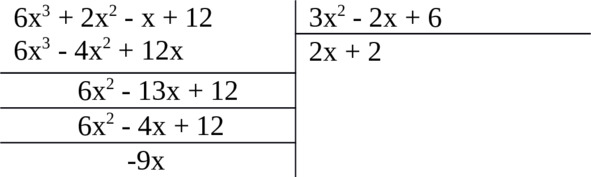
Целая часть: 2x +2

Остаток: – 9x

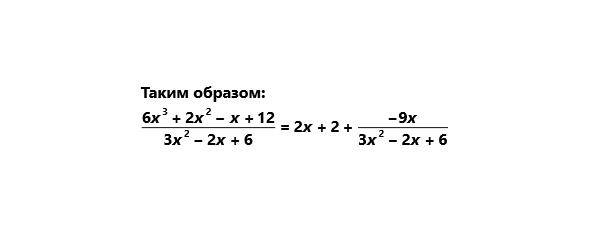
Приведём более сложный пример без дополнительных пояснений.

Целая часть: 3t2 – 7t +5

Остаток: 34t – 37

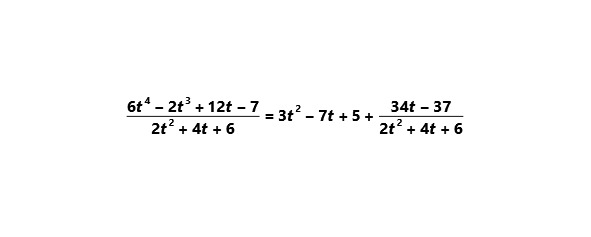
Среди частных случаев деления многочлена на многочлен выделим делимость двучлена xm±am на x±a.

1. Разность одинаковых степеней двух чисел делится без остатка на разность этих чисел, т.е. xm-am делится на x-a

Примеры.

(x2-a2): (x-a) =x+a

(x3-a3): (x-a) =x2+ax+a2

(x4-a4): (x-a) =x3-ax2+a2x+a3

(x5-a5): (x-a) =x4-ax3+a2x2+a3x+a4

2. Разность одинаковых чётных степеней двух чисел делится не только на разность этих чисел, но и на их сумму т.е. xm-am при чётном m делится на x+a

Примеры.

(x2-a2): (x+a) =x-a

(x4-a4): (x+a) =x3-ax2+a2x-a3

(x6-a6): (x+a) =x5-ax4+a2x3-a3x2+a4x-a5

2a. Разность одинаковых нечётных степеней двух чисел не делится на сумму этих чисел.

Например, ни x3-a3, ни x5-a5 не делятся на x+a.

2б. Так как разность чётных степеней делится на x-a и на x+a, то она делится и на x2-a2.

Примеры.

(x4-a4): (x2-a2) =x2+a2

(x6-a6): (x2-a2) =x4+a2x2+a4

(x8-a8): (x2-a2) =x6+a2x4+a4x2+a6

3. Сумма одинаковых степеней двух чисел никогда не делится на разность этих чисел.

Например, ни x2+a2, ни x3+a3 не делятся на x-a.

4. Сумма одинаковых нечётных степеней двух чисел делится на сумму этих чисел.

Примеры.

(x3+a3): (x+a) =x2-ax+a2

(x5+a5): (x+a) =x4-ax3+a2x2-a3x+a4

4а. Сумма одинаковых чётных степеней двух чисел не делятся ни на разность, ни на сумму этих чисел.

Например, x6+a6 не делится ни на x-a, ни на x+a.

Запомнить эти формулы необязательно, но уметь их применять необходимо.

Для удобства и упорядочивания вышеизложенных сведений можно составить такую таблицу.

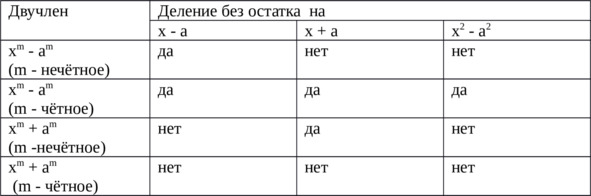
Возведение в степень n двучлена a+b.

(a+b) n=an+k1×an-1×b+k2×an-2×b2+…+bn (эта формула называется биномом Ньютона).

Где коэффициенты k (биноминальные коэффициенты) определяются из треугольника Паскаля.

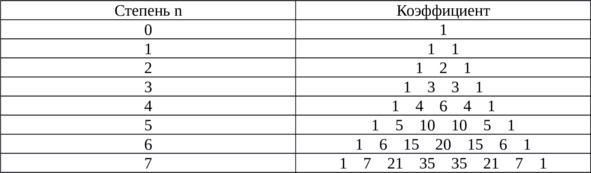
Треугольник Паскаля – таблица бесконечная. Вершина таблицы и боковые стороны каждой строки имеют единицы. Остальные числа (в середине) равны сумме 2-ух чисел, которые находятся в предыдущей строке (над ними).Вы можете легко это проверить, а также потренироваться в составлении коэффициентов для степени 8. Теперь, зная секрет этой таблицы, вы можете без труда вычислить необходимые коэффициенты. Запомните только, что таблица начинается с нулевой степени.

Примеры.

(a+b) 4=a4+4a3b+6a2b2+4ab3+b4

(a+b) 6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6

Разложение многочлена на множители.

1 способ. Вынесение общего множителя за скобки.

Если все члены многочлена содержат в качестве множителя одно и то же выражение, его можно «вынести за скобки».

С этим способом мы косвенно ознакомились раньше. Приведём только пару примеров.

Примеры.

4x2y3+8xy2z=4xy2 (xy+2z)

9a2b2—3ab2c+12abc2=3ab (3ab-bc+4c2)

2 способ. Способ группировки.

Многочлен разбивается на несколько групп, в каждой из групп выносится за скобки общий множитель, после чего в скобках оказывается одинаковое выражение, которое в свою очередь выносится за скобки.

Примеры.

5x3+10x2+3x+6=5x2 (x+2) +3 (x+2) = (x+2) (5x2+3)

20x3—12y3+8xy2—30x2y=20x3—30x2y+8xy2—12y3=10x2 (2x-3y) +

4y2 (2x-3y) = (2x-3y) (10x2+4y2)

При этом способе важно иметь в виду, что выражение a-b можно всегда представить в виде – (b-a). Поэтому, если множители отличаются только знаками, их всегда можно сделать одинаковыми.

Например:

6ab-2cb+9cd-27ad=2b (3a-c) +9d (c-3a) =2b (3a-c) -9d (3a-c) =

(3a-c) (2b-9d)

3 способ. С помощью формул сокращённого умножения.

Примеры.

9x2—1= (3x-1) (3x+1)

4x2+4x+1= (2x+1) 2

4 способ. Разложение квадратного трёхчлена ax2+bx+c=

=a (x-x1) (x-x2)

где x1 и x2-корни квадратного уравнения ax2+bx+c=0

О решении квадратных уравнений мы поговорим позже.

А сейчас просто проиллюстрируем данный способ

одним примером.

Пример.

2x2+13x-24=2 (x-3/2) (x+8) = (2x-3) (x+8)

Сначала решается квадратное уравнение

2x2 +13x -24 = 0 и находятся его корни x1=3/2, x2=-8

Потом по формуле делается разложение.

Как правило, при разложении многочлена приходится комбинировать вышеперечисленными способами, но начинать преобразования, если это возможно, с вынесения общего множителя за скобки.

Пример 1. Разложить на множители многочлен 36x3+24x+4x

Решение: Вынесем общий множитель 4x за скобки.

36x3+24x2+4x=4x (9x2+6x+1)

Трёхчлен 9x2+6x+1 можно представить в виде квадрата двучлена:

9x2+6x+1= (3x+1) 2

Таким образом, 36x3+24x2+4x=4x (3x+1) 2

Пример 2. Разложить на множители многочлен xy3—3y3+xy2z-3y2z

Решение: Вынесем за скобки общий множитель y2:

xy3—3y3+xy2z-3y2z=y2 (xy-3y+xz-3z)

Сгруппировав первый член со вторым и третий с четвёртым, разложим на множители многочлен: xy-3y+xz-3z

xy-3y+xz-3z=y (x-3) +z (x-3) = (x-3) (y+z)

Окончательно получим:

xy3—3y3+xy2z-3y2z=y2 (x-3) (y+z)

Пример 3. Разложить на множители многочлен: a2—4ab-9+4b2

Решение: Сгруппируем первый, второй и четвёртый члены многочлена. Полученный трёхчлен можно представить в виде квадрата разности.

(a2—4ab+4b2) -9= (a-2b) 2—9

Полученное выражение не что иное, как разность квадратов:

(a-2b) 2—9= (a-2b) 2—32= (a-2b-3) (a-2b+3)

Таким образом, a2—4ab-9+4b2= (a-2b-3) (a-2b+3).

Тестовые задания к теме 2

тест 1

тест 2

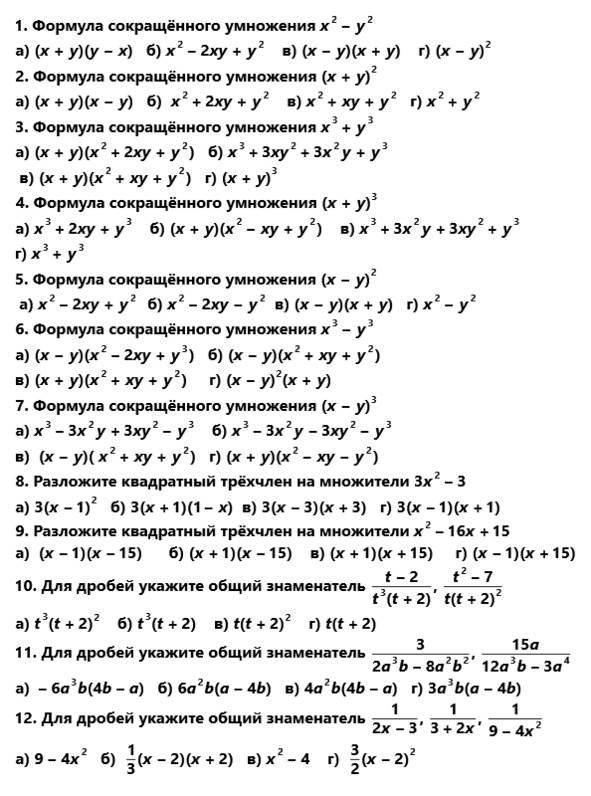
тест 3

тест 4

тест 5

тест 6

ЗАДАЧИ

Тема 3

Уравнение, общие сведения. Равносильные уравнения. Основные приёмы решения уравнений. Классификации уравнений. Решение простейших линейных и квадратных уравнений, а также уравнений приводящихся к квадратным

Понятие уравнения является одним из основных понятий алгебры. От того как вы освоите решение уравнений зависит ваше дальнейшее продвижение по усвоению более сложного материала. Поэтому отнеситесь к этой теме с должной серьёзностью.

Итак, равенство, содержащее переменную, называется уравнением. Корни уравнения – значение переменных, обращающие уравнение в верное равенство.

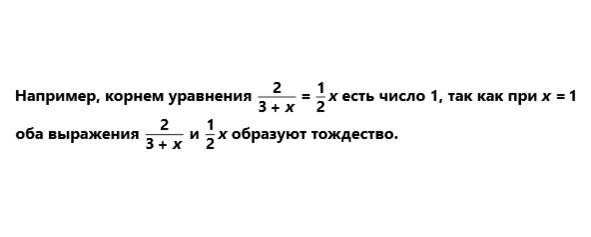
Уравнение может иметь один, два, три и т.д корня, бесчисленное множество корней или не иметь их вовсе.

Упомянутое выше уравнение имеет один корень.

Уравнение (6-x) (12-x) (3+x) = 0 имеет три корня: 6, 12, -3. Действительно, каждое из этих чисел обращает в нуль один из множителей произведения (6-x) (12-x) (3+x) и само произведение соответственно.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.