
Полная версия:
Репетитор по математике. Алгебра

Репетитор по математике. Алгебра
М. Л. Фартушняк
Дизайнер обложки М. Л. Фартушняк
© М. Л. Фартушняк, 2022
© М. Л. Фартушняк, дизайн обложки, 2022
ISBN 978-5-0056-3547-1
Создано в интеллектуальной издательской системе Ridero
Введение или как работать с этой книгой
«Репетитор по математике. Алгебра» -это вторая книга серии. Первую книгу «Репетитор по математике. Арифметика» вы можете скачать в электронном виде практически из любого книжного магазина в Интернете.
1. Почему репетитор? Название возникло сразу. Не потому, что подобных названий почти нет. Судите сами, это ведь не учебник, где весь учебный материал подаётся от более простого к сложному. В учебнике существует тенденция перескакивания с одной темы на другую, а потом возвращение к уже более сложным заданиям. В репетиторе такого нет. Если вы начали изучать какую-то тему, то изучаете её от начала и до конца. Кроме этого, в репетиторе теоретический материал подан в самом необходимом, минимальном объёме без каких-либо доказательств и выведения формул. Это также и не справочник, где существует множество формул, определений, таблиц, где много теоретического материала, но почти нет практического применения теоретических знаний. Цель же репетитора – обучение практическим навыкам решения разнообразных математических задач. Наиболее похож репетитор на практикум, там тоже большое внимание уделяется практическим занятиям, но в отличие от практикума, где почти нет теоретического материала, в репетиторе он присутствует. Кроме этого, в данном учебном пособии есть тестовые задания, которые, как правило, отсутствуют в учебниках, справочниках, практикумах.
2. Кому прежде всего будет полезна эта книга? Репетитор ориентирован на основные задания, которые могут встретиться на выпускных экзаменах за курс средней школы и на вступительных экзаменах в высшие учебные заведения. Поэтому данное пособие прежде всего станет незаменимым помощником именно для данных категорий учащихся. Он также может быть применим и учителями выпускных классов средней школы, а также тем, кто хочет повысить свою математическую грамотность и научиться решать типовые математические задачи. Автор отдаёт себе отчёт в том, что никакое учебное пособие не заменит реального живого репетитора, который сможет подкорректировать и направить свои усилия на те разделы математики, в которых ученик разбирается не совсем хорошо. Увы, книга лишена такой возможности. Она может служить только дополнением к занятиям с реальным репетитором. Однако репетитор стоит немалых денег и не у всех есть возможность его нанять. Поэтому данное учебное пособие является хоть и неполной, но альтернативой. Ещё будучи учителем в школе, автор обратил внимание, что овладеть основными математическими навыками может практически любой человек. Есть только небольшой процент людей, которые не могут этого сделать по разным объективным причинам. Остальные не знают математику и не умеют решать математические задачи, потому что, или не хотят, или не хватает времени, или просто в жизни это может не пригодится, или лень заниматься каждый день. Таким людям я не рекомендую открывать репетитор. Вы не добьётесь желаемого результата и будете винить во всём автора. А для тех, кто решил серьёзно заняться изучением математики – добро пожаловать на страницы этого пособия. Если хотя бы половине этих людей репетитор поможет, автор будет считать, что его труд не был напрасным.
3. Чем же репетитор отличается от других учебных пособий? Прежде всего простотой подачи материала. Автор общается с обучаемым и указывает на характерные ошибки, которые могут встретиться при решении задач. В репетиторе показано решение типовых задач, а также задач повышенной трудности. Каждая задача или пример решается досконально с пояснениями, что позволяет усвоить базовые навыки даже людям, которые считали, что математика не для них.
4. О структуре данной книги. Вся книга поделена на 23 темы. В каждой теме есть необходимый минимум теоретического материала, примеры решения задач. В конце каждой темы даются один или несколько тестовых заданий (кроме тем 12 и 21) и задачи для самостоятельного решения.
Поговорим отдельно о каждой из этих составляющих.
Теоретический материал. Как было уже сказано ранее, это тот необходимый минимум, без которого невозможно обойтись при решении заданий. Если формула выведена крупным шрифтом – её необходимо запомнить. Тоже самое касается формулировок и прочих элементов теории. Таких обязательных элементов для запоминания в книге немного. Обучение построено по американской системе, где от учащегося не требуется зазубривание теоретического материала, а предпочтение отдаётся только навыкам его применения на практике. Поэтому, при самостоятельном решении задач автор разрешает пользоваться формулами. Запоминание формул произойдёт автоматически при практическом их применении. В конце книги собран и изложен в кратком виде весь теоретический материал. Им вы можете пользоваться при решении задач. Это не значит, что теоретический материал можно совсем не изучать или изучить бегло. Как я уже сказал, в конце каждой темы есть тестовые задания и без базовых знаний теоретического материала, вы вряд ли сможете их пройти.
Примеры решения задач. В репетиторе рассмотрены решения как базовых типовых задач, так и задач повышенной сложности. Многие задания взяты из конкурсных задач по математике, которые были предложены абитуриентам при поступлении в высшие учебные заведения в 70 – 80х годах прошлого столетия. Поверьте, если вы научитесь решать эти задачи, то любой экзамен вам будет по плечу. Часть заданий взята из экзаменационных задач за курс средней школы, часть из других источников. Автор уважает авторские права других, поэтому в конце книги дан список использованной литературы. Как было сказано выше, все примеры решения задач приведены с подробными пояснениями.
Тестовые задания. К каждой теме предложено один или несколько тестовых заданий, в зависимости от объёма теоретического материала. Каждое тестовое задание включает 12 вопросов с четырьмя вариантами ответов, один из которых является правильным. Оценивание тестовых заданий производится по 12-ти бальной системе. Чтобы не путаться, привожу перевод 12-ти бальной системы в 5-ти бальную.
12 баллов – оценка 5+
11 баллов – 5
10 баллов – 5-
9 баллов – 4+
8 баллов – 4
7 баллов – 4-
6 баллов – 3+
5 баллов – 3
4 балла – 3-
3 балла – 2+
2 балла – 2
1 балл – 2 —
Я надеюсь, что последние шесть строчек вам не понадобятся при оценивании тестовых заданий. Только все должно быть по-честному. Помните, если вы будете не объективны, то в первую очередь обманите сами себе.
Теперь, как оценивать тестовые задания. За каждое правильное тестовое задание начисляется 1 балл. По количеству набранных баллов и выставляется итоговая оценка по 12-ти бальной системе. Например, вы ответили правильно на 7 вопросов-это оценка 4-. При 11-ти верных ответах имеете оценку 5, а при 12-ти имеете максимум 5+.
Продолжительность тестирования – 25—30 минут. Выделите для тестирования отдельный день. Берите чистый лист бумаги и вперёд. Тесты – это не только интересно, но и познавательно. Желательно пройти все предложенные тесты (но не более двух за один день), в конце книги имеются ответы на тестовые задания для проверки. Не стоит в них заглядывать раньше времени.
Задачи для самостоятельного решения. Автор сознательно не выделял какими-то знаками задания повышенной сложности и считает, что такое приём способствует более спокойному решению задач без излишнего волнения и стресса. В процессе решения вы сами сможете понять, сложна для вас данная задача или нет. Притом сложность задачи – это субъективная оценка. Некоторые с лёгкостью могут решать подобные задачи, а вот более простые в нашем понимании могут вызвать затруднение. Если вы поняли, что можете приступать к решению задач, то не медлите. Каких-то ограничений по количеству решаемых задач в день нет. Когда поняли, что устали, то занятие можно прекратить, но хотя бы 30 – 40 минут в день вы должны уделять решению задач. Это не обязательно делать изо дня в день. Через какое-то время можно сделать себе 1- 2-х дневный перерыв. Но с отдыхом не затягивайте. Почувствовав, что немного отдохнули и есть свободное время, приступайте снова к решению задач. Автор рекомендует решить все задачи, которые есть в разделе для самостоятельного решения. Решив какую-то задачу, загляните в раздел «ответы» и, убедившись, что вы все решили правильно, продолжайте дальше. Если ваш ответ не совпадает с ответом в конце книги, рекомендуется ещё раз пройтись по своему решению и выявить ошибки. Если вы их не обнаружили, то загляните в раздел «Указания к решению задач». Он находится после раздела ответов. Прочитав указания к решению задач (они есть практически ко всем задачам), снова приступайте к решению сложной для вас задачи. К задачам для самостоятельного решения есть полные и подробные решения, которые находятся в соответствующем разделе. Но это последний раздел, в который вам следует заглянуть. Это в том случае, когда задача не решается без посторонней помощи. Не злоупотребляйте этим разделом, иначе вы так никогда и не научитесь решать математические задачи. Постарайтесь ограничиться только разделом «Указания к решению задач». Этого бывает достаточно, чтобы понять свою проблему и попытаться её искоренить.
В конце книги, как я уже сказал, находится справочный раздел, ответы к тестовым заданиям, ответы к задачам для самостоятельного решения, указания к решению задач, решение задач. Кроме этого, там же находится список использованной литературы. Структура книги максимально удобна для использования. А в начале книги предложены условные математические обозначения, которые будут встречаться в дальнейшем.
Автор будет благодарен за любые замечания и обнаруженные неточности и ошибки при написании этого пособия. А также будет рад любому мнению и практическим советам от учителей и преподавателей математики по улучшению данной книги.
некоторые математические обозначения

Алгебра
Это один из основных разделов математики. В нем мы научимся преобразовывать алгебраические выражения, решать разнообразные уравнения, неравенства, а также их системы (в том числе показательные и логарифмические). Большое внимание уделим текстовым задачам, а также ознакомимся с понятием «функция» и научимся строить графики различных функций. Просьба, по возможности, решить все предложенные задачи в этом разделе и пройти все тестовые задания.
Тема 1
Возведение в степень, свойства степени, корни, действия с корнями
Возвести число в целую степень n, значит повторить его сомножителем n раз т.е.

Вторая степень называется квадратом, третья – кубом.

Запомните!
1) Первой степенью числа называют само это число.
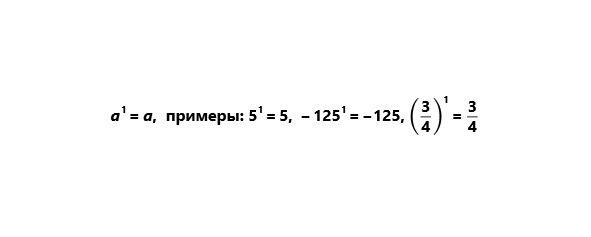
2) Любое число (кроме нуля) в нулевой степени есть единица.
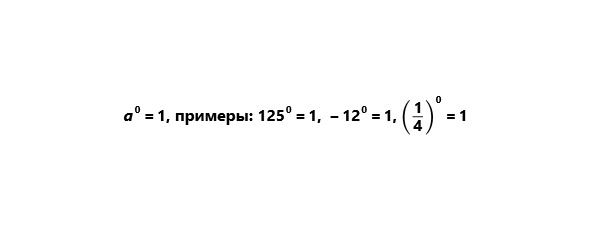
3) Нуль в любой неотрицательной степени есть нуль.

4) Единица в любой степени есть единица.
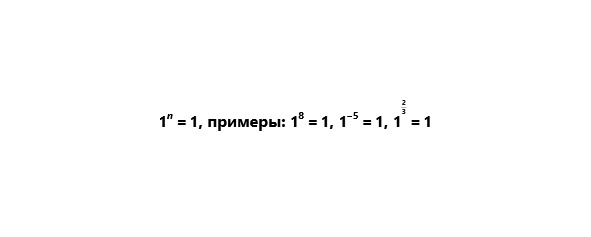
Отрицательный показатель степени.

Дробный показатель степени.
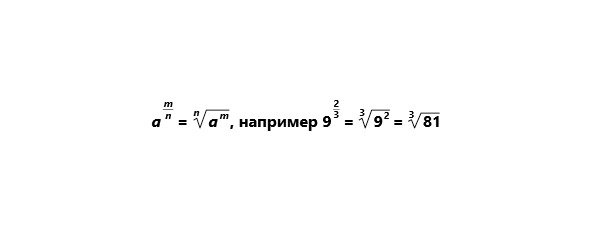
Дробный отрицательный показатель степени
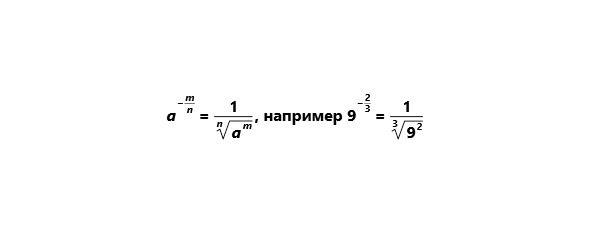
Теперь рассмотрим свойства степени. Для удобства мы составили таблицу, в котором привели примеры не только с натуральными показателями степени, но и с рациональными и действительными.

Необходимые пояснения к свойствам степени.
Первые два свойства указывают на действия со степенями с одинаковыми основаниями. При умножении таких степеней их показатели складываются (свойство 1), при делении – вычитаются (свойство 2). Третье свойство – это свойство возведения степени в степень – показатели степени перемножаются (свойство 3).
Следующие два свойства – это возведение в степень произведения (свойство 4) и частного (свойство 5). Притом, свойство 4 справедливо для любого числа сомножителей. Применение данных правил позволяет существенно облегчить вычисления.


Извлечение корня есть нахождение основания степени по степени и её показателю. Записывается это так

Основные свойства корня.
1) Если за корнем следует степень, равная показателю корня,
то корень можно опустить, например

2) Если подкоренное число имеет степень равную
показателю корня, то оно равно модулю подкоренного числа.
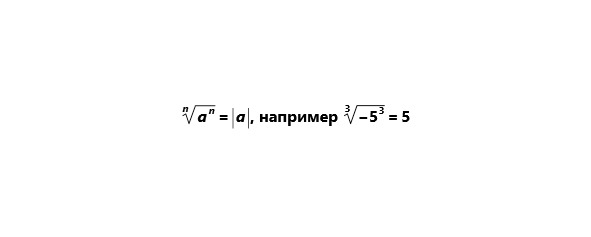
Основные действия с корнями (все эти правила справедливы при
a≥0 и b≥0)
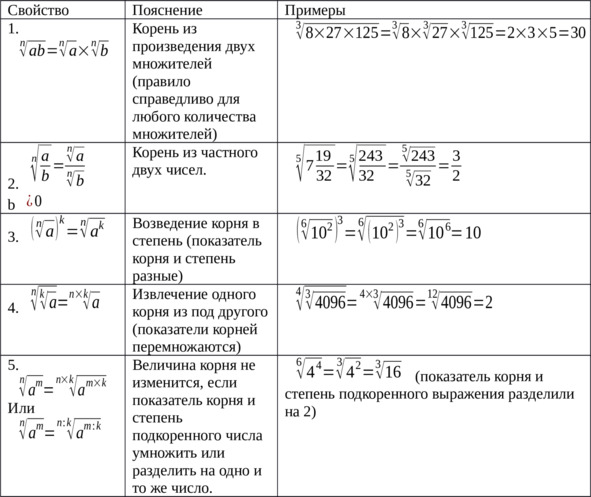
Все вышеизложенные правила позволяют существенно облегчить вычисления.
Рассмотрим две операции: внесение множителя под знак корня и вынесение множителя из-под знака корня при решении задач.


Очень часто при преобразованиях пользуются приёмом уничтожения иррациональности в знаменателе или числителе дроби. Такой метод позволяет упростить приближенные вычисления. Рассмотрим его на примере.

.
Уничтожив иррациональность в знаменателе, мы пришли к такому результату, что нам необходимо разделить приближенное число на целое, что намного точнее и проще, чем делить приближенное число на приближенное и проводить вычисления с большим количеством значащих цифр, чтобы получить два верных знака после запятой.
Тестовые задания к теме 1
Тест 1

Тест 2

Тест 3

Тест 4

Тест 5

Задачи

Тема 2
Одночлен. Многочлен. Преобразование алгебраических выражений. Формулы сокращённого умножения. Разложение многочлена на множители
Мы подошли к одной из самых важных тем алгебры. Ведь без задания на преобразование алгебраических выражений не обходится практически ни один экзамен по математике. Сразу предупреждаю, такие преобразования сложны и требуют не только знаний, но и внимания, смекалки, терпения.
Для начала мы ознакомимся с понятиями «одночлен» и «многочлен».
Одночленом называется произведение двух или нескольких сомножителей каждый из которых есть либо число, либо буква, либо степень буквы.
Например, 6a2x, 2c, 3b3c2, -10y7, -7abc.
Одночлены состоят из коэффициента (числового множителя) и буквенной части.
6a2x = 6 (коэффициент) × a2x (буквенная часть).
Отдельно взятое число, буква или степень буквы тоже рассматриваются как одночлен. Например, -5 (одночлен без буквенной части), с и c5 (одночлены, в которых коэффициент равен 1).
Одночлены называются подобными, если они одинаковы или отличаются только коэффициентами.
Например, 7x2y3, -5x2y3, -x2y3 – подобны.
Сложение двух или нескольких одночленов возможно только тогда, когда среди слагаемых имеются подобные.
Например, 6x2y2 +9x2y2 – 7x2y2 = 8x2y2.
Здесь мы суммировали коэффициенты, оставив буквенную часть без изменений. Такое действие называется приведением подобных членов.
Можно этот пример решить иначе, вынеся общий множитель за скобки:
6x2y2 +9x2y2 – 7x2y2 = (6+9—7) x2y2 = 8x2y2.
Как мы видим, вынесение общего множителя за скобки – операция, идентичная приведению подобных членов.
Произведение двух или нескольких одночленов можно упростить лишь тогда, когда в них входят некоторые степени одних и тех же букв или числовые коэффициенты. При этом показатели степеней у соответствующих букв складываются, числовые коэффициенты перемножаются.
Пример: -10x2y×3x3y2 × (-xy3) = -10×3× (-1) (x2x3x) (yy2y3) = 30x6y6.
Для лучшего понимания, мы расписали это действие более подробно, хотя оно довольно прозрачное и может делаться устно.
Частное двух одночленов можно упростить, если делимое и делитель содержат некоторые степени одних и тех же букв или числовые коэффициенты. При этом показатель степени делителя вычитается из показателя степени делимого, а числовой коэффициент делимого делится на числовой коэффициент делителя.
Пример: 6x3y8z7: 2xy5z3 = 3x2y3z4.
Здесь числовой коэффициент делимого разделили на числовой коэффициент делителя, вычли показатели степени буквы x (3—1=2), буквы y (8—5=3) и буквы z (7—3=4).
При делении двух одночленов могут возникнуть две ситуации, которые требуют дополнительного пояснения.
1.Если показатели степени у некоторой буквы в делимом и делителе одни и те же, то в частное эта буква не войдёт (ведь нулевая степень любого числа равна единице).
Пример: 12x3y4: 4x3y2 =3y2.
2.Если показатель степени какой-нибудь буквы в делимом меньше, чем показатель степени той же буквы в делителе, то вычитание даёт отрицательную степень этой буквы.
Пример: 8x3y5: 2x5y3 = 4x-2y2 = (4y2) / (x2)
При возведении одночлена в степень используется правило возведения степени в степень.
Пример: Возведём одночлен 2a4b2 в четвертую степень.
(2a4b2) 4 = 24 (a4) 4 (b2) 4 = 16a16b8.
Не забывайте, что показатели степеней при данном правиле перемножаются.
Сумма одночленов называется многочленом.
Например, 4x2y +3a -7b2 – многочлен, состоящий из суммы одночленов 4x2, 3a, -7b2.
При сложении и вычитании многочленов снова получается многочлен.
Пример. Сложим многочлены x3 +2x2y2 – 7x2 + y и 3x3 – x2y2 +5x2 – 3y.
Составим сумму многочленов, затем раскроем скобки и приведём в полученном многочлене подобные члены.
(x3+2x2y2—7x2+y) + (3x2– x2y2 +5x2 – 3y) = x3 +3x3 +2x2y2 – x2y2 – 7x2 +5x2+ y – 3y = 4x3 + x2y2 – 2x2 – 2y.
Здесь одновременно с раскрытием скобок мы сгруппировали подобные члены (для удобства вычислений).
Аналогично, производится и вычитание многочленов. Не забывайте, если перед скобкой стоит знак «минус», то все члены, заключаемые в скобки, меняют свой знак на противоположный.
Пример. (4x2y – 7x3 +5y – 3) – (-2x2y +5x3– 3y +2) =4x2y – 7x3 +5y -3 +2x2y -5x3 +3y – 2 = 6x2y – 12x3 +8y – 5.
Произведение многочленов.
Произведение одночлена и многочлена всегда можно представить в виде многочлена.
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
Схема: a× (b+c) =a×b+a×c (открытие скобок)
Например:
– 4x3 (2y3– x +6) = -4x32y3 + (-4x3 (-x)) + (-4x3 ×6) = -8x3y3 +4x4 – 24x3.
Мы выписали здесь промежуточные вычисления, хотя, в принципе, без этой записи можно обойтись.
Умножение многочлена на многочлен.
Произведение многочлена на многочлен равно сумме всех возможных произведений каждого одночлена одного из многочленов на каждый одночлен другого.
Схема: (a+b) × (c+d) =a×c+a×d+b×c+b×d
Пример. (3x2 – 6x +2) × (4x3 – 3x) = 12x5 – 9x3 – 24x4 +18x2 +8x3 – 6x =
= 12x5 – 24x4 – x3 +18x2 – 6x.
Существуют частные случаи умножения многочленов, которые называются формулами сокращённого умножения многочленов. Их желательно запомнить.
1. (a+b) 2 =a2+2ab+b2 (квадрат суммы)
2. (a-b) 2=a2—2ab+b2 (квадрат разности)
3. (a-b) (a+b) =a2-b2 (разность квадратов)
4. (a+b) 3=a3+3a2b+3ab2+b3 (куб суммы)
5. (a-b) 3=a3—3a2b+3ab2-b3 (куб разности)
6. (a+b) (a2-ab+b2) =a3+b3 (сумма кубов)
7. (a-b) (a2+ab+b2) =a3-b3 (разность кубов)
Примеры: (2ma2 +0.1nb2) 2 = 4m2a4 +0.4mna2b2 +0.01n2b4
(5x3 – 2y3) 2 = 25x6 – 20x3y3 +4y6
(0.2a2b + c3) (0.2a2b – c3) = 0.04a4b2 – c6
(5ab2 +2a3) 3 = 125a3b6 +150a5b4 +60a7b2 +8a9
Предлагаю вам самим узнать, какие формулы были использованы в этих примерах.
Деление многочленов.
1. Деление многочлена на одночлен.
Частное от деления многочлена на одночлен равно сумме частных, полученных от деления каждого слагаемого многочлена на одночлен.
Схема:
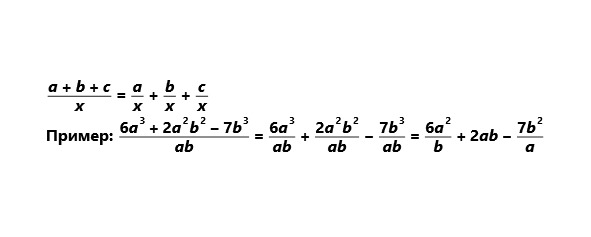
2. Деление многочлена на многочлен в общем случае можно выполнить с остатком, подобно тому, как это делается при делении целых чисел.
Разделить многочлен P на многочлен Q значит найти многочлен M (частное) и N (остаток) удовлетворяющий двум требованиям: 1) должно соблюдаться равенство MQ+N=P и 2) степень многочлена N должна быть ниже степени многочлена Q.
Процесс нахождения частного M и остатка N аналогичен процессу деления с остатком многозначного числа на многозначное. Перед делением члены делимого и делителя располагается в порядке убывания степеней главной буквы.
Например, разделим 6x3 +2x2 – x +12 на 3x2 – 2x +6
Запись деления:
1.Делим первый член делимого 6x3на первый член делителя 3x2. Результат 2x – первый член частного.
2.Умножаем полученный член на делитель 3x2 – 2x +6, результат 6x3 – 4x2 +12x записываем под делимым.
3.Вычитаем члены результата из соответствующих членов делимого, сносим следующий по порядку член делимого, получаем 6x2 – 13x +12
4. Первый член остатка 6x2 делим на первый член делимого, результат 2 есть второй член частного.
5. Множим полученный второй член частного на делитель, результат 6x2 – 4x +12 подписываем под первым остатком.
6. Вычитаем члены этого результата из соответствующих членов первого остатка, получаем второй остаток: -9x. Его степень меньше степени делителя. Деление закончено.
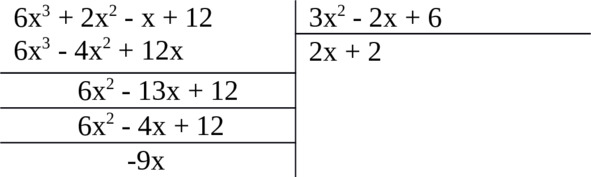
.



