
Полная версия:
Введение в машинное обучение

Едилхан Амиргалиев, Равиль Мухамедиев
Введение в машинное обучение
Министерство образования и науки Республики Казахстан
Рекомендован к изданию УМО РУМС
Рецензенты:
Барахнин В. Б., д.т.н., профессор, НГУ, Россия, Новосибирск
Никульчев Е. В., д.т.н., профессор, МИРЭА, Россия, Москва
Маткаримов Б. Т., , д.т.н., профессор, Назарбаев университет, Казахстан, Нурсултан
Эту книгу мы посвящаем памяти наших родителей Валерии, Ильгиза, Несипхана и Задан, которые дали нам жизнь, любовь и возможность стать теми, кто мы есть.
Равиль Ильгизович Мухамедиев,Едилхан Несипханович АмиргалиевПредисловие
Авторы по роду своей педагогической деятельности и в рамках своих научных исследований довольно часто соприкасались с проблемами искусственного интеллекта, распознавания образов, в том числе машинного обучения. Естественно, нам приходилось поглубже изучать эти проблемы, чтобы успешно оперировать методами машинного обучения, которые становятся «модными» инструментами, применяемыми многими специалистами для решения оптимизационных задач в «плохо формализованных» областях исследования.
Машинное обучение наиболее быстро развивающая часть науки о данных. Новые, успешные модели появляются ежегодно, а их модификации и примеры приложений практически ежедневно. Поэтому написание какого-нибудь подробного пособия сопряжено с трудностями выбора такого содержания, которое с одной стороны не будет слишком поверхностным изложением самых последних достижений, а с другой стороны не погрузиться в разбор моделей, которые на практике используются уже не столь часто. Авторы постарались следовать от простого к сложному, уделив особое внимание аппарату искусственных нейронных сетей, поскольку последние достижения в области искусственного интеллекта связаны с моделями глубоких нейронных сетей. Вместе с тем разбор особенностей различных моделей хоть и полезен, но не достаточен для практических применений. Поэтому авторы включили специальные разделы, описывающие оценку качества моделей, предобработку данных и оценку параметров, которые в той или иной мере присутствуют в каждом приложении машинного обучения. На наш взгляд имеющийся набор сведений достаточен для успешного старта на пути применения машинного обучения на практике. Учебник обогащен материалами на основе опыта преподавания авторами предметов по искусственному интеллекту, распознаванию образов и классификации, компьютерному зрению, обработке естественного языка и машинному обучению в ведущих вузах Республики Казахстан: КазНУ имени аль-Фараби, КазНИТУ имени К. Сатпаева, Международном университете информационных технологий, Университете имени Сулеймана Демиреля, Казахстанско-Британском Техническом университете, а также материалами и результатами, полученными в рамках научных исследований по выполненным научным проектам грантового и программно-целевого финансирования в течение последних 10 лет.
Любая книга – это большой и часто длительный труд, который не мог бы состояться без помощи многих людей. Авторы выражают искреннюю признательность рецензентам В. Б. Барахнину, Е. В. Никульчеву и Б. Т. Маткаримову, потратившим драгоценное время для улучшения качества текста и давшим ценные советы по содержанию учебника. Большую работу по коррекции текста и тестированию примеров книги проделали Адилхан Сымагулов, Марина Елис, Ян Кучин. Ян Кучин оказал большую помощь в рамках проекта по созданию классификатора литологических типов урановых скважин РК. Рустам Мусабаев представил результаты эксперимента, посвященные высокопроизводительным вычислениям.
Не претендуя на полноту изложения всех возможностей методов машинного обучения, авторы в данной книге необходимый материал подали в двух частях, как введение в теорию и введение в практику машинного обучения. Практическая часть насыщена лабораторными занятиями и разборами кодов примеров, что поможет читателям поглубже освоить методы применения машинного обучения. Архив с примерами программ читатели могут скопировать по адресу: https://www.dropbox.com/s/xtxicveo5lwmu8z/ML_book_ExamplesLabs_v.1.0.zip?dl=0.
Авторы надеются, что учебник окажет помощь преподавателям вузов, магистрантам, докторантам и многим разработчикам, занимающимся прикладными задачами.
За все ошибки и неточности, которые заинтересованный читатель увидит в тексте, несут ответственность только авторы. Мы будем признательны за конструктивные замечания и уточнения, которые читатели могут направить на адреса электронной почты: mukhamediev.ravil@gmail.com, amir_ed@mail.ru. Дополнительный материал авторы планируют размещать на сайте geoml.info.
Введение
Машинное обучение (Machine Learning – ML) – направление науки, относящееся к большой области, называемой искусственным интеллектом. Это направление исследований развивается уже несколько десятков лет. Оно обеспечивает потребности практики в тех ситуациях, когда строгая математическая модель задачи отсутствует или является неприемлемо сложной. В рамках этого направления рассматривают алгоритмы, которые способны обучаться, то есть, по существу, находить закономерности в данных. ML как научное направление изучает методы кластеризации, классификации и регрессии. В результате для специалистов по разработке программного обеспечения предлагаются методы обработки данных, которые реализуют часть интеллектуальных способностей, присущих человеку. К их числу относится способность обучаться, переобучаться, классифицировать объекты реального мира, предсказывать на основе накопленного опыта. В настоящее время именно с ML связано наибольшее количество ожиданий по реализации «умных» программ и сервисов (Smart Services). Например, по оценкам Gartner в 2017 году (рисунок 1.1), ML порождает наибольшие ожидания в развитии технологий. Более того, значительная часть новых технологий связана с ML.
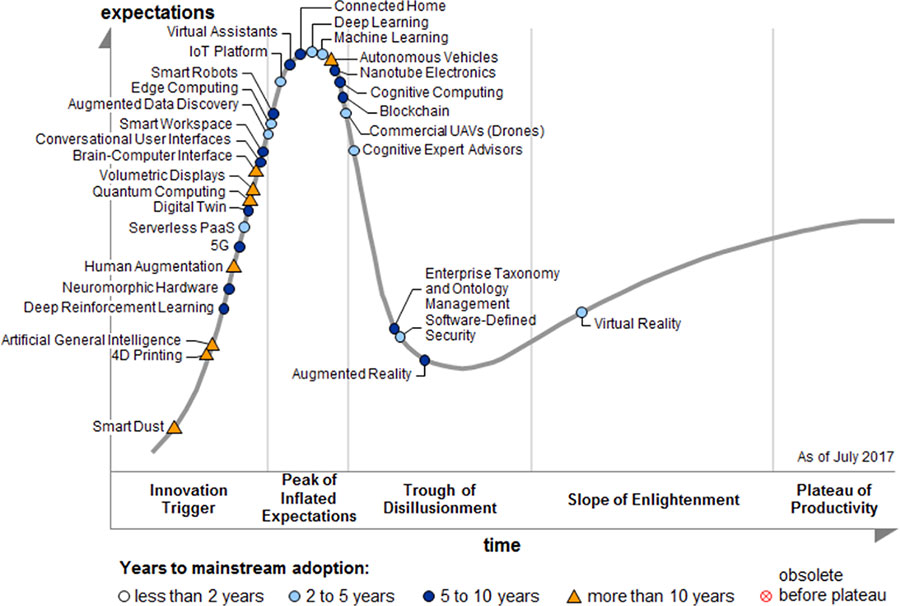
Рисунок 1.1. Инновационные триггеры, ожидания, разочарования и продуктивность технологий [[1]]
Организациям и исследователям, занимающимся разработкой наукоемких технологий, рекомендуется рассматривать следующие научные области: Smart Dust, Machine Learning, Virtual Personal Assistants, Cognitive Expert Advisors, Smart Data Discovery, Smart Workspace, Conversational User Interfaces, Smart Robots, Commercial UAVs (Drones), Autonomous Vehicles, Natural-Language Question Answering, Personal Analytics, Enterprise Taxonomy and Ontology Management, Data Broker PaaS (dbrPaaS) и Context Brokering.
Таким образом, ML из сферы научных исследований перешло в сферу инженерных дисциплин. Знание ML необходимо системным аналитикам, инженерам программного обеспечения, разработчикам встроенных систем, программистам. Общие понятия о ML должны быть также у специалистов по управлению.
В настоящее время существует несколько программных систем и библиотек программ, реализующих алгоритмы машинного обучения с той или иной степенью гибкости. Например, система RapidMiner [[2]], один из лучших интегрированных пакетов, обеспечивает подготовку данных, создание моделей и тем самым интеграцию их в бизнес-процессы организации. Matlab, широко известный пакет прикладных программ и язык программирования компании MathWorks, предоставляет несколько сотен функций для анализа данных – от дифференциальных уравнений и линейной алгебры до математической статистики и рядов Фурье. GNU Octave использует совместимый с Matlab язык высокого уровня и в целом имеет высокую совместимость с Matlab. Это позволяет использовать и его для прототипирования систем машинного обучения. Функции Octave доступны онлайн [[3]], загрузить систему можно по ссылке [[4]]. Отметим, что Octave содержит несколько предустановленных библиотек, список которых можно просмотреть по ссылке https://octave.sourceforge.io/packages.php.
Однако наиболее часто упоминается язык программирования Python и ряд библиотек, использующих его для реализации алгоритмов машинного обучения. Например, развитые библиотеки программ по машинному обучению могут быть вызваны из среды Anaconda (https://www.anaconda.com/), основой которой является язык Python. Библиотеки numpy, matplotlib, pandas, sklearn, предустановленные в Anaconda, используются в данном пособии в качестве практической основы для решения задач классификации и регрессионного анализа.
Настоящая книга состоит из двух основных частей.
В первой части, которую можно назвать «теоретической», мы рассматриваем модели машинного обучения, основные метрики оценки качества работы алгоритмов ML, задачи и методы подготовки данных и т.п. В ней приводятся примеры и необходимые пояснения обсуждаемых моделей. Материал этой части может составить основу лекционного курса по машинному обучению. Эта часть состоит из семи глав.
В первой главе машинное обучение рассматривается в контексте дисциплин искусственного интеллекта (ИИ). Несложная классификация дисциплин ИИ дает понимание места и роли ML в задачах обработки данных.
Во второй главе обсуждаются математические модели классических алгоритмов машинного обучения. В эту группу мы, разумеется, включили не все возможные алгоритмы, однако представленные алгоритмы дают представление о разнообразии классических моделей ML.
В третьей главе мы достаточно подробно обсуждаем методы оценки качества классификации и регрессии.
Четвертая глава посвящена методам и средствам предобработки табличных данных.
Пятая глава кратко описывает специфические задачи обработки больших объемов данных.
Шестая глава содержит введение в модели глубокого обучения.
Седьмая глава посвящена еще до конца не решенному вопросу объяснения результатов работы моделей ML.
Вторая часть включает методические рекомендации по порядку выполнения лабораторных работ, достаточно объемный практикум машинного обучения и описание проектной работы. Каждая лабораторная работа содержит необходимые пояснения и одну или несколько задач. Выполнение этих задач позволит учащимся получить хорошие навыки в использовании библиотек машинного обучения и решении практических задач. Дополнительная глава описывает практическую задачу по интерпретации данных электрического каротажа скважин по добыче урана и ставит несколько задач по обработке этих данных. Материалы этой главы можно использовать для выполнения проекта по применению машинного обучения в задачах добычи полезных ископаемых.
Любая книга не свободна от недостатков. Как говаривал незабвенный Козьма Прутков, «нельзя объять необъятное». Множество интересных вопросов машинного обучения остались за рамками книги. Однако авторы надеются, что представленный материал покроет некоторый дефицит в систематическом, практико ориентированном изложении сведений о классических методах машинного обучения, а лабораторные работы позволят студентам овладеть практическими навыками, необходимыми для решения задач машинного обучения на базовом уровне.
Часть I. Математические модели и прикладные методы машинного обучения
1. Искусственный интеллект и машинное обучение. Составные части искусственного интеллекта
Искусственный интеллект (ИИ) – это любые программно-аппаратные методы, которые имитируют поведение и мышление человека. ИИ включает машинное обучение, обработку естественного языка (Natural Language Processing – NLP), синтез текста и речи, компьютерное зрение, робототехнику, планирование и экспертные системы [[5]]. Схематично компоненты ИИ показаны на рисунке 1.1.
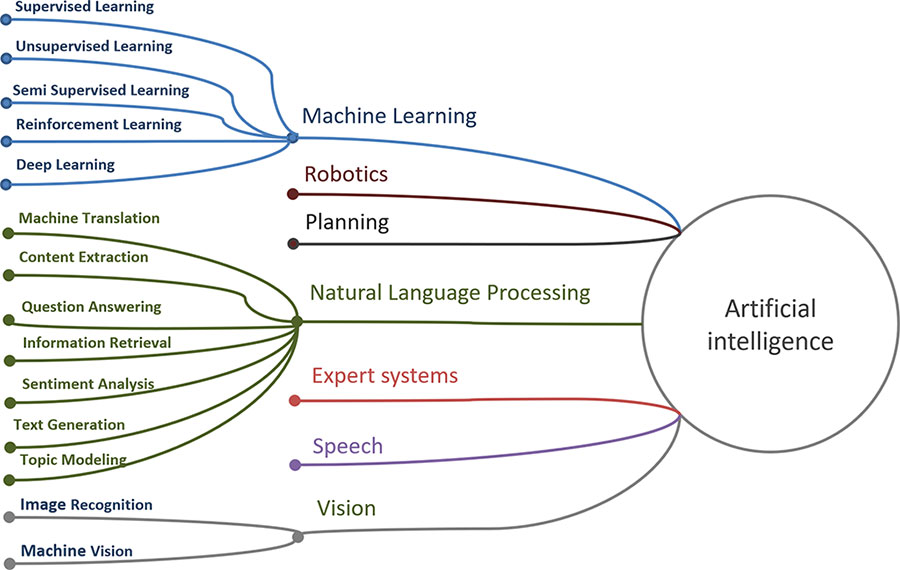
Рисунок 1.1. Подразделы искусственного интеллекта
Машинное обучение как дисциплина, являющаяся частью обширного направления, именуемого «искусственный интеллект», реализует потенциал, заложенный в идее ИИ. Основное ожидание, связанное с ML, заключается в реализации гибких, адаптивных, «обучаемых» алгоритмов или методов вычислений.
Примечание. «Метод вычислений» – термин, введенный Д. Кнутом для отделения строго обоснованных алгоритмов от эмпирических методов, обоснованность которых часто подтверждается практикой.
В результате обеспечиваются новые функции систем и программ. Согласно определениям, приведенным в [[6]]:
– Машинное обучение (ML) – это подмножество методов искусственного интеллекта, которое позволяет компьютерным системам учиться на предыдущем опыте (то есть на наблюдениях за данными) и улучшать свое поведение для выполнения определенной задачи. Методы ML включают методы опорных векторов (SVM), деревья решений, байесовское обучение, кластеризацию k-средних, изучение правил ассоциации, регрессию, нейронные сети и многое другое.
– Нейронные сети (NN) или искусственные NN являются подмножеством методов ML, имеющим некоторую косвенную связь с биологическими нейронными сетями. Они обычно описываются как совокупность связанных единиц, называемых искусственными нейронами, организованными слоями.
– Глубокое обучение (Deep Learning -DL) – это подмножество NN, которое обеспечивает расчеты для многослойной NN. Типичными архитектурами DL являются глубокие нейронные сети, сверточные нейронные сети (CNN), рекуррентные нейронные сети (RNN), порождающие состязательные сети (GAN), и многое другое.
Перечисленные компоненты ИИ показаны на рисунке 1.2.
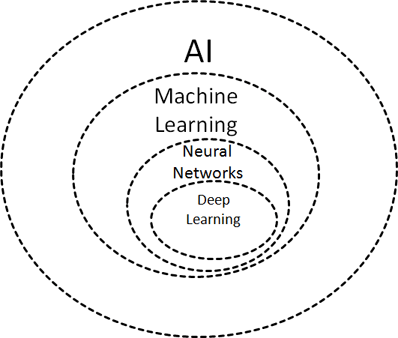
Рисунок 1.2. Искусственный интеллект и машинное обучение
Сегодня машинное обучение успешно применяется для решения задач в медицине [[7], [8]], биологии [[9]], робототехнике, городском хозяйстве [[10]] и промышленности [[11], [12]], сельском хозяйстве [[13]], моделировании экологических [[14]] и геоэкологических процессов [[15]], при создании системы связи нового типа [[16]], в астрономии [[17]], петрографических исследованиях [[18], [19]], геологоразведке [[20]], обработке естественного языка [[21], [22]] и т.д.
1.1. Машинное обучение в задачах обработки данных
Массивы накопленных или вновь поступающих данных обрабатываются для решения задач регрессии, классификации или кластеризации.
В первом случае задача исследователя или разработанной программы ˗ используя накопленные данные, предсказать показатели изучаемой системы в будущем или восполнить пробелы в данных.
Во втором случае, используя размеченные наборы данных, необходимо разработать программу, которая сможет самостоятельно размечать новые, ранее не размеченные наборы данных.
В третьем случае исследователь имеет множество объектов, принадлежность которых к классам, как и сами классы, не определена. Необходимо разработать систему, позволяющую определить число и признаки классов на основании признаков объектов.
Таким образом, задача обработки данных называется регрессией, когда по некоторому объему исходных данных, описывающих, например, предысторию развития процесса, необходимо определить его будущее состояние в пространстве или времени или предсказать его состояние при ранее не встречавшемся сочетании параметров; классификацией, когда определенный объект нужно отнести к одному из ранее определенных классов, и кластеризацией, когда объекты разделяются на заранее не определенные группы (кластеры).
В случаях, когда нет строгих формальных методов для решения задач регрессии, классификации и кластеризации, используются методы ML [[23]].
В настоящее время методы МL делят на пять классов [[24], [25], [26], [27], [28]]: обучение без учителя (Unsupervised Learning – UL) [[29]] или кластерный анализ, обучение с учителем (Supervised Learning – SL) [[30]], полууправляемое обучение, включая самообучение (Semi-supervised Learning – SSL), обучение с подкреплением (Reinforcement Learning – RL) и глубокое обучение (Deep Learning). Методы машинного обучения решают задачи регрессии, классификации, кластеризации и снижения размерности данных (рисунок 1.3).
Задачи кластеризации и снижения размерности решают с использованием методов UL, когда множество заранее не обозначенных объектов разбивается на группы путем автоматической процедуры, исходя из свойств этих объектов [[31], [32]]. Указанные методы позволяют выявлять скрытые закономерности в данных, аномалии и дисбалансы. Однако в конечном счете настройка этих алгоритмов все же требует экспертного оценивания.
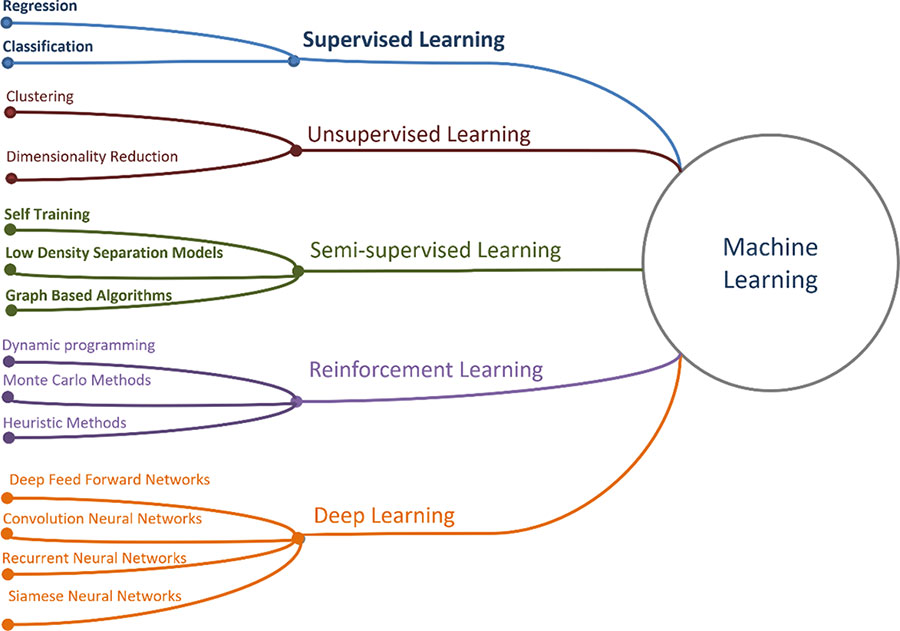
Рисунок 1.3. Основные классы методов машинного обучения [[33]]
Методы SL решают задачу классификации или регрессии. Задача классификации возникает тогда, когда в потенциально бесконечном множестве объектов выделяются конечные группы некоторым образом обозначенных объектов. Обычно формирование групп выполняется экспертом. Алгоритм классификации, используя эту первоначальную классификацию как образец, должен отнести следующие не обозначенные объекты к той или иной группе, исходя из свойств этих объектов.
Методы SL часто разделяются на линейные и нелинейные в зависимости от формы (гиперплоскости или гиперповерхности), разделяющей классы объектов. В двумерном случае линейные классификаторы разделяют классы единственной прямой, тогда как нелинейные классификаторы – линией (рисунок 1.4).
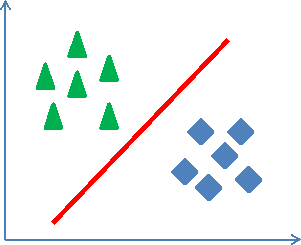
a)
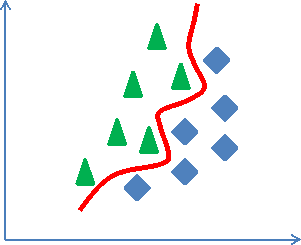
b)
Рисунок 1.4. Линейный (а) и нелинейный (b) классификаторы
В таблице 1.1 перечислены пять классов методов машинного обучения и выделены алгоритмы, которые рассматриваются в нижеследующих разделах.
Таблица 1.1. Методы машинного обучения для анализа данных
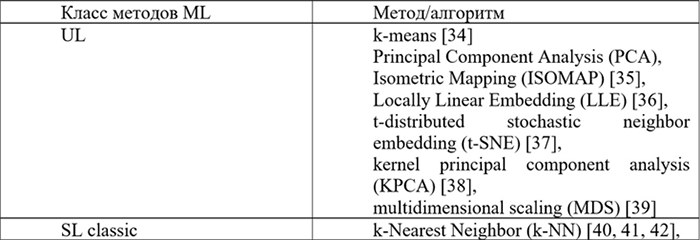
Более детальная иерархическая классификация классических методов машинного обучения приведена в приложении 2.
1.2. Программное обеспечение для решения задач машинного обучения
Библиотеки машинного обучения можно разделить на две большие группы: базовые библиотеки, реализующие широкую гамму классических алгоритмов машинного обучения, импорт и экспорт данных и их визуализацию, и библиотеки, предназначенные для создания и работы с моделями глубокого обучения. В приведенном ниже перечне выделены пакеты, которые далее используются при выполнении задач настоящего учебника.
Базовые библиотеки:
Обработка массивов и матриц – numpy
Обработка данных, включая импорт и экспорт данных – pandas, pytables
Анализ данных – scipy, scikit-learn, opencv
Визуализация данных- matplotlib, bokeh, seaborn
Многоцелевые – sympy, cython
Пакеты для работы с моделями глубокого обучения (Deep Learning frameworks):
Caffe/Caffe2, CNTK, DL4J, Keras, Lasagne, mxnet, PaddlePaddle, TensorFlow, Theano, Torch, Trax
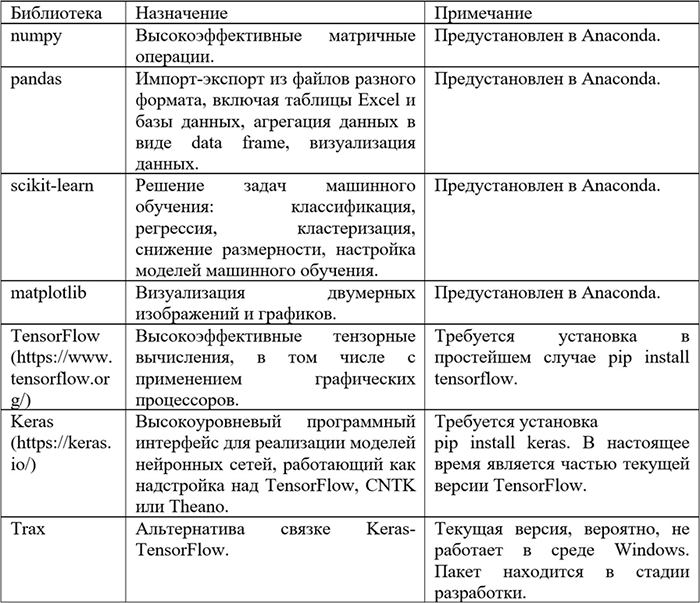
Таблица 1.2 кратко описывает наиболее часто применяемые пакеты программ.
Таблица 1.2. Пакеты программ, применяемые для решения задач машинного обучения
1.3. Схема настройки системы машинного обучения
Применение методов машинного обучения в задачах, для которых строгая математическая модель отсутствует, а имеются только экспертные оценки, часто бывает оптимальным способом решения. Обучаемая система, в частности, искусственная нейронная сеть, способна воспроизвести закономерность, которую сложно или невозможно формализовать. В задачах «обучения с учителем» часто затруднительно определить качество экспертных оценок. К таким задачам относятся, в частности, и задачи выявления рисков заболеваний, оценки качества продуктов, распознавания речи, предсказания уровня котировок акций на финансовых рынках, распознавания литологических типов на урановых месторождениях по данным электрического каротажа. Несмотря на то, что эксперты задают перечень актуальных признаков объектов, диапазоны измеряемых физических величин могут перекрываться, а экспертные оценки могут быть противоречивыми или содержать ошибки. В качестве такого примера на рисунке 1.5 показаны точки, соответствующие породам (по экспертным оценкам), или, иначе говоря, литологическим типам (песок, гравий, глина и т.п.), в пространстве трех видов электрического каротажа (кратко обозначены ИК, ПС, КС) для одного из урановых месторождений Казахстана.
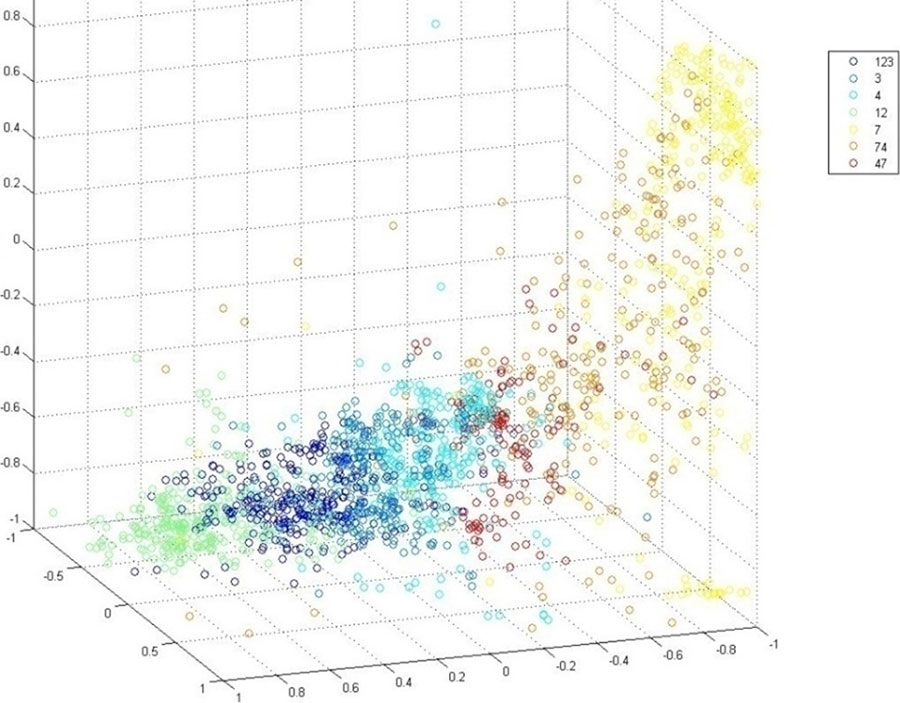
Рисунок 1.5. Ответы экспертов в трехмерном (ИК, КС и ПС) пространстве признаков
Примечание. Подробнее о задаче классификации литологических типов на урановых месторождениях с применением методов машинного обучения рассказывается в монографии [[34]].
Номера пород, приведенных на рисунке и обозначенных разными цветами, описываются в главе «Проект по созданию классификатора литологических типов на основании каротажных данных урановых скважин РК».
Видно, что точки, соответствующие разным литологическим типам, существенно перемешаны в пространстве признаков и, соответственно, не могут быть разделены простыми (например, линейными) способами.
Кроме этого, данные, представленные для классификации, могут содержать аномальные значения и ошибки, связанные с физическими особенностями процессов их получения. Соответственно, и обученная система может интерпретировать данные с ошибками.
В процессе разработки комплекса программ обработки данных инженер по данным выполняет анализ применимости методов машинного обучения, определяет способы подготовки данных для использования указанных методов, выполняет сравнение алгоритмов с целью выявления лучшего алгоритма, решающего задачу.
Общая схема настройки методов машинного обучения на решаемую задачу приведена на рисунке 1.6.
В соответствии с этой схемой нам необходимо определить саму задачу, которая должна быть решена с помощью машинного обучения. Затем собрать данные, предобработать их, выбрать алгоритмы или методы, обучить или настроить методы, оценить результаты. В задачах обучения с учителем данные должны быть разделены на тренировочную (train), тестовую (test) и для некоторых задач проверочную (validation) части. Перечисленные этапы на самом деле части итеративного процесса, который инженер по данным повторяет с целью добиться наилучшего результата работы. Этот процесс не обязательно приводит к наилучшему результату, но его цель – добиться лучшего из возможных при тех данных, которые имеются в распоряжении исследователя.
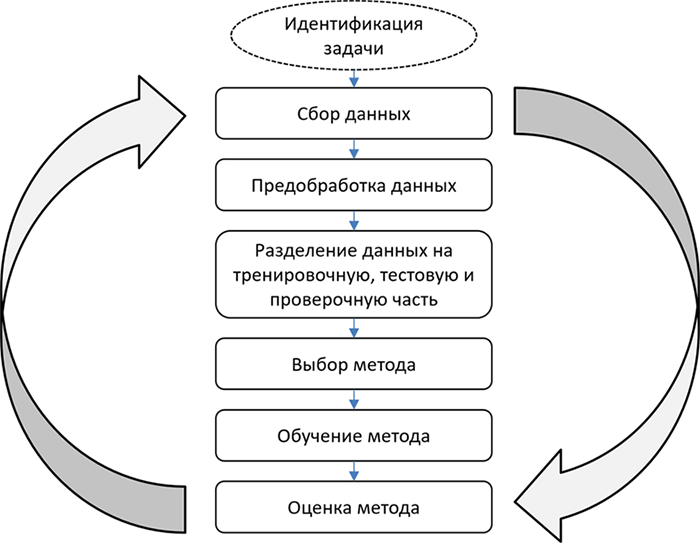
Рисунок 1.6. Циклический процесс настройки модели машинного обучения для решения задачи
1.4. Контрольные вопросы
1. Искусственный интеллект – это часть обширного направления, называемого «искусственные нейронные сети»?
2. Глубокое обучение как направление исследований и разработок – часть машинного обучения?
3. Чем отличаются алгоритмы «обучения с учителем» от кластеризации?
4. Что такое линейный классификатор и чем он отличается от нелинейного?
5. Процесс настройки модели машинного обучения – это _____?
6. Укажите типы машинного обучения, относящиеся к классу «обучение с учителем» (Supervised Learning).
7. Какие библиотеки машинного обучения используются в данном пособии?
8. Укажите типы машинного обучения, относящиеся к классу «обучение без учителя» (Unsupervised Learning).
9. Вы получили заданный набор обучающих данных. Что делать, если результаты работы алгоритма машинного обучения не удовлетворяют потребностям практики?
2. Классические алгоритмы машинного обучения
2.1. Формальное описание задач машинного обучения
Формальная постановка задачи машинного обучения (задача обучения по примерам или задача обучения с учителем) заключается в следующем [[35]].
Пусть имеются два пространства: Ob (пространство допустимых объектов), Y (пространство ответов или меток) и (целевая) функция.
Определено отображение y: Ob → Y, которое задано лишь на конечном множестве объектов (обучающей выборке (прецедентах) (sample set)) размером m:
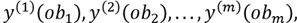
то есть известны метки объектов ob1, ob2,…, obm. Требуется построить алгоритм A («обучить»), который по объекту ob определяет значение y(ob) или «достаточно близкое» значение, если допускается неточное решение.
Другими словами, зная значения целевой функции на обучающей выборке, требуется найти удовлетворительное приближение к ней в виде А.



