Очерки теории музыкального моделирования. Книга вторая

Если мы будем двигаться, пропуская каждый раз два элемента (с первого на четвертый), то вернемся к исходному элементу через 4 шага. В результате получится уменьшенный септаккорд.

Если двигаться, пропуская три элемента (с первого на пятый), то вернемся к исходному через 3 шага, получив в итоге увеличенное трезвучие.

Если пропускать пять элементов (с первого на седьмой), то через два шага вернемся к исходному пункту, получив тритон.

Совсем иная картина получится, если двигаться в любом из направлений, пропуская четыре элемента (по квартам), или шесть элементов (по квинтам), что в итоге одно и то же. Ровно через 12 шагов, перебрав по пути все элементы круга, мы возвращаемся к исходному пункту.

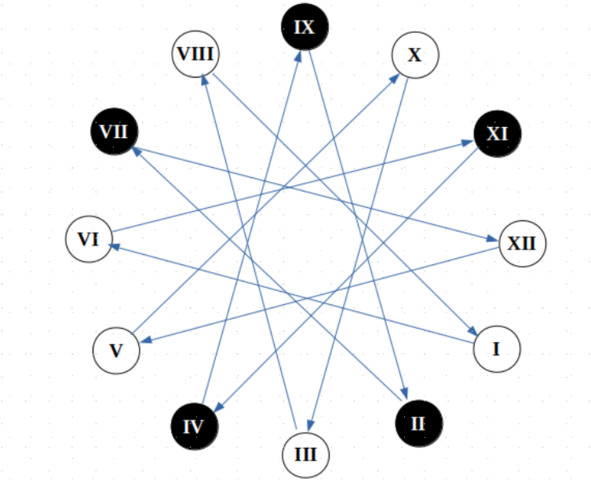
Переход от полутонового круга к квинтовому

В итоге этого путешествия получается квартовый (или квинтовый) круг:

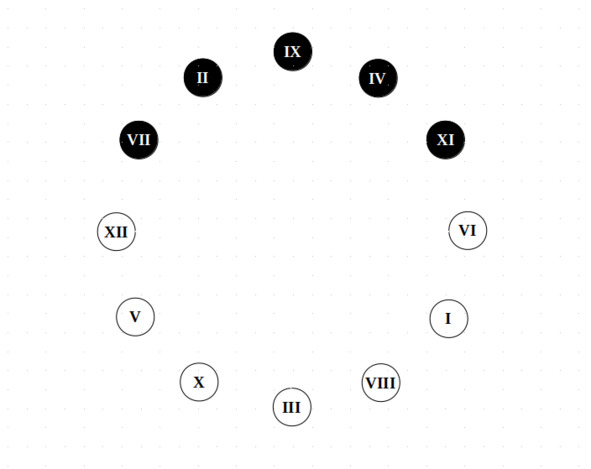
Квинтовый круг

Обратим внимание, что те же самые диаметры играют роль симметрии и антисимметрии, что и в первом случае. Ре-Ля бемоль (Соль диез) – ось симметрии, Фа-Си – ось антисимметрии.

Кроме того (и в этом нетрудно убедиться самостоятельно), если повторить все наши манипуляции, проделанные с полутоновым кругом, по отношению к квинтовому кругу и попробовать двигаться по нему, пропуская сначала один элемент, потом два, потом три, мы опять получим сначала целотонный звукоряд, затем уменьшенный септаккорд, затем увеличенное трезвучие. То есть, обнаруживается высокая степень структурного подобия между полутоновым и квинтовым кругами.

Далее, выполненную для полутонового круга двенадцати-шаговую процедуру можно повторить теперь для квинтового круга. В результате мы вновь получим полутоновый круг. Таким способом они превращаются друг в друга.

Впрочем, это превращение можно осуществить и более простым путем. Надо из шести диаметров нашего круга выбрать либо все четные, либо все нечетные. А затем элементы, располагающиеся на них поменять местами:

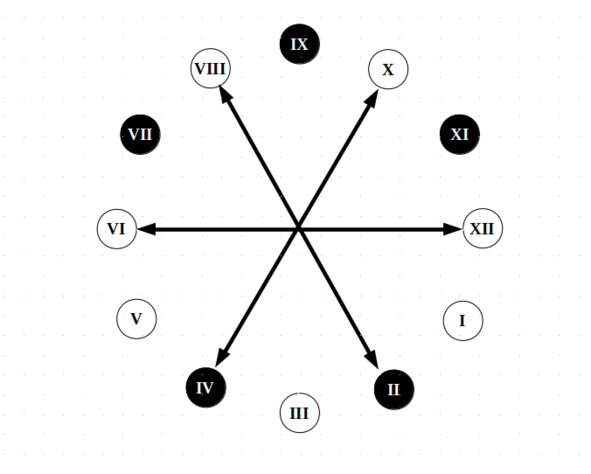
Второй способ перехода

Далее мы можем очень просто «развернуть» этот квинтовый круг в квинтовую прямую, приняв в качестве в качестве идентификационного признака для каждого ее элемента способ порождения данного элемента. Для обозначения этих элементов мы используем привычные названия – до, до диез, ре бемоль и т. д.

После всех проделанных преобразований (манипуляций) система приобрела вид композиции из двух шкал – квинтовой и полутоновой, каждая их который имеет два представления – линейное и круговое. Линейные представления вполне удобно использовать для того, чтобы сделать наглядным характер взаимодействия этих шкал, что мы уже использовали в первом выпуске «Очерков теории музыкального моделирования». Повторим эту схему и в данном тексте:

Квинто-полутоновая схема

На данном шаге нашего исследования мы можем констатировать некоторые важные особенности строения музыкальной моделирующей системы:

– Данная система включает в себя две взаимосвязанные шкалы, упорядочивающие отношения ее элементов – полутоновую и квинтовую.

– Каждая из них имеет два представления:

– линейное – полутоновая прямая и квинтовая прямая

– круговое – полутоновый круг и квинтовый круг.

– Существует преобразование, позволяющее превратить квинтовый круг в полутоновый, а полутоновый в квинтовый. Это преобразование можно выполнить двумя способами. Во-первых, путем движения по кругу. Но не подряд, а шагом по 5 или 7 элементов. Во-вторых, путем взаимного перемещения элементов, находящихся на противоположных концах трех четных либо трех нечетных диаметров.

– Отношение полутоновой и квинтовой шкал характеризуется высоким уровнем симметрии.

– Эта симметрия не означает их смысловой идентичности и взаимозаменяемости. Элементы (кванты) этих шкал – квинта и полутон – существенным образом отличаются по своему звучанию и, как мы знаем из соответствующих разделов первой книги, по своей модельной функции. Полутоновая шкала – пространство. Квинтовая шкала – энергия.

– Полутоновая шкала и все, происходящее на ней, воспринимается непосредственно и достаточно легко. Квинтовая шкала носит значительно более скрытый, латентный, внутренний характер. Изменения, происходящие на ее уровне, воспринимаются, так сказать, на стадии результата. Например, превращение мажорного трезвучия в минорное мы слышим непосредственно, но разность в 7 шагов по квинтовой шкале между мажорной и минорной терцией от нас скрыта.

Теперь несколько слов о взаимодействии трех шкал, которых мы коснулись в данном очерке – полутоновой, квинтовой и натурального обертонового ряда. Безусловно доминирующий в музыкальной практике (музыкальной культуре) строй, делящий октаву на 12 равных частей, является исключительным по важности (и не исключено, что единственно возможным) компромиссом между собственно темперированным строем, пифагоровым строем и натуральным строем, каждый из которых опирается на одну из перечисленных выше трех шкал. Этот компромисс действует благодаря некоторой гибкости нашего музыкального восприятия, допускающего не абсолютно точное соответствие реального физического звучания, и соотнесения этого звучания со шкалами музыкальной моделирующей системы, выступающими в качестве логической, структурной ее основы. Физически (математически) эти три шкалы совпадают лишь приблизительно. И если их продолжать достаточно долго, то погрешности будут все более нарастать. Чем точнее мы соблюдаем точность относительно какой-то одной их шкал, тем более отклоняемся от требований других двух.

Заметим, что, если бы октава была разделена не на двенадцать, а скажем на тринадцать или четырнадцать частей, то вышеописанный компромисс (приблизительное совпадение) был бы невозможен. Не в этом ли состоит столь удивительное и столь ценное неповторимое качество, рождаемое делением октавы именно на двенадцать частей?

* * * * *

Наш анализ строения музыкальной системы далек от завершения. Но даже на данном его этапе мы можем видеть сколь сложной и высоко организованной является эта система. В определенном смысле она сама является художественным произведением. Произведением, не созданным каким-то одним человеком – пусть даже гением. Это произведение является продуктом постепенного развития музыкальной культуры. Его изучение – не менее интересно и не менее поучительно, чем анализ самой прекрасной сонаты или симфонии.

Практически на всех уровнях своей организации, во всех своих составляющих эта система обнаруживает присутствие человека, общества, культуры. Физическое здесь неразрывно связано с психическим, материальное с духовным, а действие природных законов переплетено с деятельностью людей.

Возвращаясь к проблемам диатоники

Быть может, кто-то удивится и скажет, – какие еще проблемы могут быть связаны с диатоникой? Тем более в наше-то время! Для нас додекафония и серийная техника – прошлый век. Еще Пушкин вложил в уста Сальери слова: «для меня это так ясно, как простая гамма». А диатоника – это, собственно, и есть «простая гамма».

С другой стороны, мы знаем – по крайней мере, подозреваем, – что абсолютно простых вещей и явлений в мире не существует. Любая простота может обнаружить внутреннюю сложность. Почему же «простой гамме» запрещено таить внутреннее богатство и сложность? Зададим себе вопрос: а если бы в ней не было внутренней (скрытой) сложности, если бы не было неисследованных глубин, откуда берется тот внутренний, смысловой потенциал, который не вычерпан за многие века? Нет, что-то тут не так. Поэтому, ничего не утверждая заранее, хочу всего лишь поставить под вопрос тезис о простоте «простой гаммы».

В книге «Очерки теории музыкального моделирования» я уже касался вопроса о семиступенных «ладах народной музыки». И, прежде всего, вопроса о том, почему они семиступенные. Что за особое качество связано именно с таким, а не иным числом ступеней? Другой вопрос, который был поднят, связан с эмоциональным качеством, с тем, что древние греки называли «этосом» ладов. Эти вопросы были затронуты, как мне теперь представляется, слишком кратко. Кроме того, есть и другие, о которых не было сказано вовсе. Наконец, не все из того, как это было изложено тогда, удовлетворяет меня теперь. Кое-что можно было сказать проще и ясней. Потому и возвращаюсь к этой теме.

Напомню, что в рамках теории музыкального моделирования музыка рассматривается не столько с точки зрения устройства музыкальных произведений, сколько с точки зрения устройства музыкальной системы, на базе которой эти произведения формируются. Сказав слово «система» (если, конечно, мы употребляем такие слова достаточно ответственно), мы принимаем, в той или иной степени, логику системного подхода. А в этой логике система не сводится к сумме ее элементов, но представляет такое их объединение, которое дает в результате качество (системное качество), не присущее ни одному их этих элементов в отдельности. Известный термин «эмерджентность», собственно, и означает появление у системы качеств, которых не было о составляющих ее элементов до объединения их в систему.

Заметим, что системное качество (как, впрочем, и любое качество) проявляется у системы (как и у любого объекта) тогда, когда система или объект вступает во взаимодействие с другими объектами или системами. Если это взаимодействие связано с использованием данной системы в человеческой деятельности, есть все основания рассматривать системное качество в связи с функциями системы. Иными словами, системное качество в подобных случаях проявляет себя не само по себе, а в контексте человеческой деятельности. Все сказанное относится и к музыкальной системе. Нет деятельности, в которую она включена и в которой она реализует некоторые функции, – нет системного качества (качеств), а если нет системного качества – нет и системы.

В центре внимания теории музыкального моделирования находится общая для искусства отражательно-познавательная функция в ее отношении к музыкальному искусству. Это и определяет содержание вопросов, которые мы задаем в этой связи. Нас начинает интересовать, что и как способна отражать, воспроизводить, реперезентировать музыка своими специфическими средствами? Каковы ее возможности в качестве инструмента познания, мышления и коммуникации (общения)? Какие сферы реальности доступны для нее: а) только лишь акустические явления (шумы природы, голоса животных и птиц, человеческая речевая интонация), б) разнообразные формы движения (прежде всего, механического движения), в) процессы развития, а следовательно, и логика развития, или г) общие принципы мироздания? О чем бы из перечисленного ни шла речь, уместным становится вопрос о способности музыки подражать, воспроизводить предмет своего освоения в тех или иных его аспектах. Этим, собственно, и объясняется использование нами термина «моделирование». Этот термин мы используем как экспликацию (уточняющее замещение) понятия «подражание» («мимесис»).

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Примечания

1

И. В. Способин. Элементарная теория музыки. М., 1963 с. 23

2

Сохор А. Н. Музыка // Музыкальная энциклопедия. Т.3. М., 1976, стлб.730.

3

Б. Асафьев. Музыкальная форма как процесс. Книга вторая. Интонация. Музгиз, 1974, с.3

4

Б. Асафьев. Музыкальная форма как процесс. Книга первая. Издательство «Музыка», 1971, с.29)

5

И. М. Сеченов. Рефлексы головного мозга. Издательство АСТ, 2014 г., стр. 70

6

https://gufo.me/dict/dal/%D1%81%D0%BE%D0%B1%D1%8B%D1%82%D0%B8%D0%B5

7

В. И. Ленин. Собр. соч., т. XIV, с.39, изд. 4-е, 1952

8

И. В. Способин. Элементарная теория музыки. М., 1963, с.5