
Полная версия:
Альтернативный волновой анализ. Новые горизонты
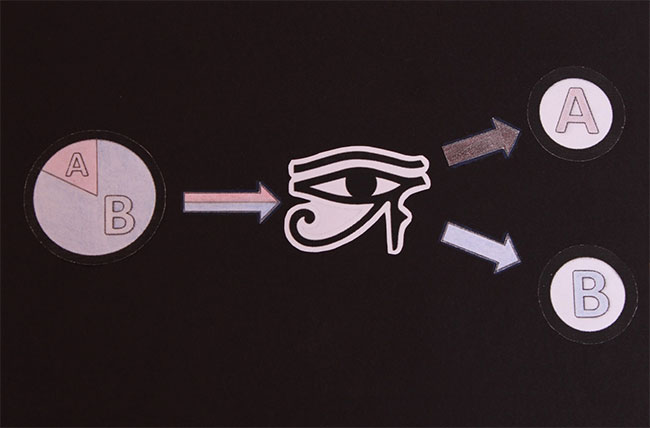
Соответственно, если доминирующей в суперпозиции является точка А, то и вероятность того, что частица займет точку А, больше. И наоборот, соответственно:

Мы рассмотрели с вами возможность частицы занять две позиции:

Однако на самом деле таких позиций может быть гораздо больше:

В общем, сколько угодно.
При этом существует лишь большая вероятность того, что частица займет одни позиции:

И меньшая вероятность того, что она займет другие позиции:
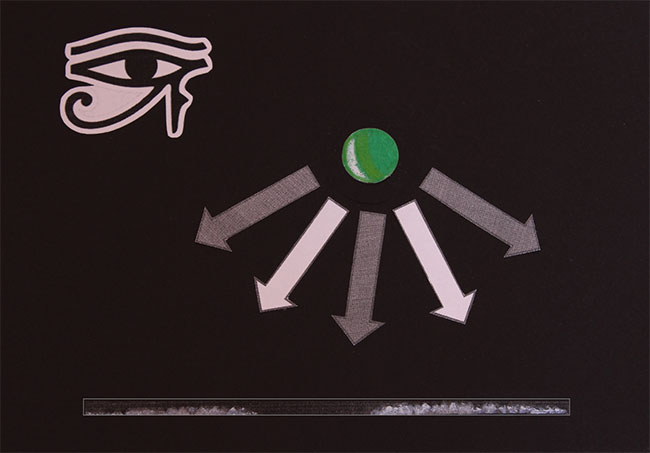
Поэтому, основываясь на этих наблюдениях, можно построить волновой график вероятностей распределения. Вероятностей того, какие позиции частица займет, а какие не займет (с большей или меньшей вероятностью):
Факт того, что таким образом можно предсказывать положение частиц, лежит в основе многих квантовых феноменов, которые называются корпускулярно-волновым дуализмом.
Аналогичным образом, с точки зрения AWA, развивается и ценовой график. Другими словами, невозможно заранее точно сказать, как поведет себя цена в будущем, так как всегда существует несколько сценариев ее развития с различными по величине (амплитуде) вероятностями.
Однако, проводя замеры, каждый раз мы можем путем вычислений определить, в какую область вероятностной кривой попадет текущая фаза. Но вернемся к волновому графику.
Как мы уже знаем, его амплитуда колебаний описывает вероятность того, какое положение частица может занять, а какое нет.
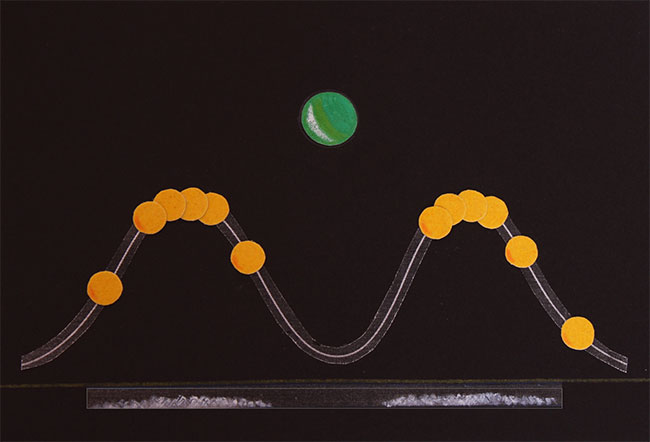
Если мы внимательно посмотрим на эту кривую, то увидим:

Волновая кривая вероятностей очень сильно напоминает концентрические стоячие волны, возникающие вокруг падающей капли.

Согласитесь, очень похоже.
Я не зря рассмотрел принцип суперпозиции в самом начале. Ведь именно принцип суперпозиции лежит в основе формирования стоячих волн, о которых речь пойдет далее. Именно поэтому я использую его при расчете волновых циклов.
Стоячие волны
Теперь давайте поговорим о том, что такое стоячие волны. Для начала рассмотрим простой пример. Прикрепим один конец веревки к стенке, а второй конец при этом начнем раскачивать.

По веревке начинает бежать волна, которая затем отразится. Мы продолжаем качать свободный конец веревки. Волны, бегущие в прямом и обратном направлениях, складываются. Но мы видим полный беспорядок.
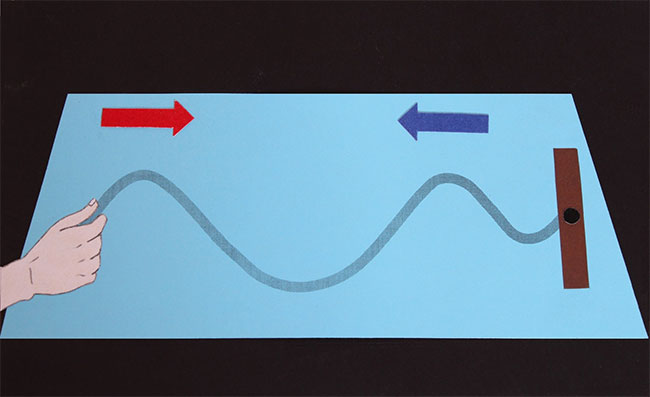
Меняем частоту колебаний до тех пор, пока не возникнет устойчивая картина стоячей волны.
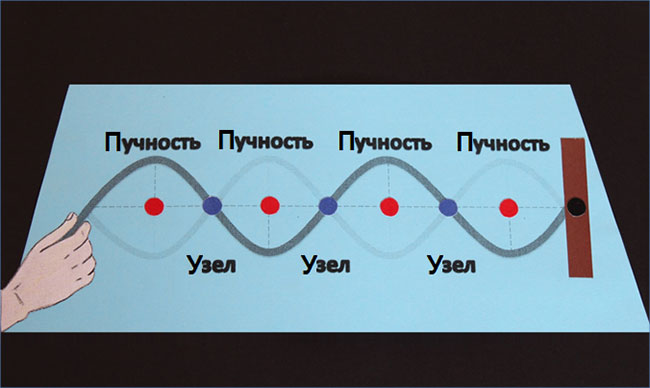
Мы видим точки волны, которые остаются на месте. Это интерференционные минимумы, или узлы стоячей волны. Также мы видим точки, колеблющиеся с максимальной амплитудой. Это интерференционные максимумы, или пучности стоячей волны. Можно увеличить частоту колебаний свободного конца веревки и также увидеть стоячую волну, но с меньшей длиной волны. Главное условие, чтобы на расстоянии между источником и стенкой укладывалось целое количество половин длины волны.
Итак, мы познакомились с простейшей иллюстрацией стоячих волн. Теперь давайте разберем стоячие волны с точки зрения физики.
Стоячая волна – это волна, которая образуется при наложении двух волн с одинаковой амплитудой и частотой, когда волны движутся навстречу друг другу (испущенная и отраженная волны).
Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн по отдельности. Это утверждение называется принципом суперпозиции (наложения) волн.
В случае, когда колебания, обусловленные отдельными волнами в каждой из точек среды, обладают постоянной разностью фаз, волны называются когерентными. При сложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других точках ослабляют друг друга. Возникающий в результате колебательный процесс называется стоячей волной.
На практике стоячие волны образуются при отражении волн от различных преград. Падающая (испущенная) на преграду волна и бегущая ей навстречу (отраженная) волна, накладываясь друг на друга, формируют стоячую волну.
Таким образом, стоячую волну можно представить как суперпозицию (сумму) двух плоских волн, распространяющихся вдоль оси X в противоположных направлениях. Уравнения двух плоских волн, распространяющихся вдоль оси X в противоположных направлениях:
ψ1 = A cos(ωt – kx + φ),
ψ2 = A cos(ωt + kx + φ).
Сложение этих функций, согласно формуле суммы косинусов дает следующее выражение:
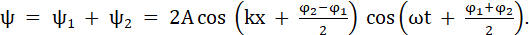
Чтобы привести это уравнение к более простому виду, выберем точку начала отсчета x, так чтобы разность φ2–φ1 стала равной 0. Аналогичным образом поступим и с точкой начала отсчета t. Ее выберем так, чтобы сумма φ1+φ2 тоже стала равной 0.
После таких преобразований формула стоячей волны будет иметь вид
ψ = 2A cos kx cos ωt
Заменив волновое число k его значением
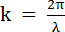
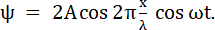
Из этого уравнения видно, что амплитуда колебаний зависит от x: в точках, координаты которых удовлетворяют условию
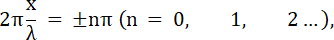
амплитуда колебаний достигает максимального значения. Эти точки называются пучностями стоячей волны.
Значения координат пучностей равны
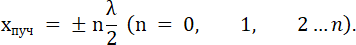
В точках, координаты которых удовлетворяют условию
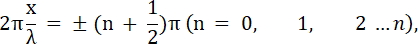
амплитуда колебаний обращается в 0. Эти точки называются узлами стоячей волны.
Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов имеют значения
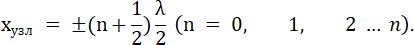
Из этих формул следует, что расстояние между соседними пучностями, так же как и расстояние между соседними узлами, равно λ/2. Пучности и узлы сдвинуты друг относительно друга на четверть длины волны λ/4.
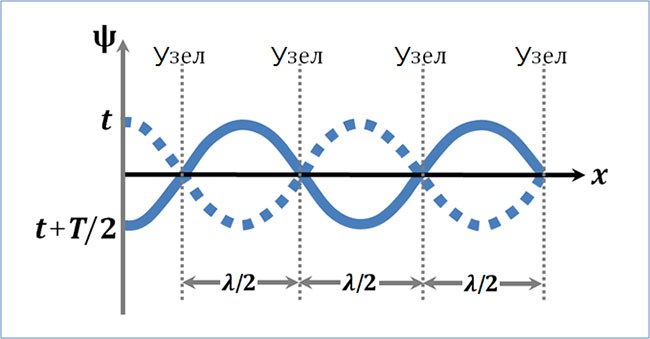
Стоячая волна не переносит энергию. Дважды за период происходит пульсация – превращение энергии стоячей волны то полностью в потенциальную энергию, сосредоточенную в основном вблизи узлов волны, то полностью в кинетическую энергию, сосредоточенную в основном вблизи пучностей волны. В результате происходит переход энергии от каждого узла к соседним пучностям и обратно.
Здесь необходимо отметить, что стоячие волны являются достаточно частым явлением в физическом мире. Они могут возникать в струнах, стержнях, жидкостях, воздушных столбах и т. д., поэтому я сделал предположение о том, что стоячие волны могут проявляться и на ценовых графиках финансовых активов.
Оставалось только найти подходящего кандидата. И такой кандидат действительно нашелся – это волновые циклы, которыми оперирует AWA.
Да-да, вы не ослышались. Именно волновые циклы выступают аналогом стоячих волн на финансовых рынках.
Но прежде чем мы продолжим, необходимо разобраться с таким понятием, как интерференция волн. Дело в том, что стоячие волны являются следствием такого фундаментального явления в физике, как интерференция волн.
Интерференция волн
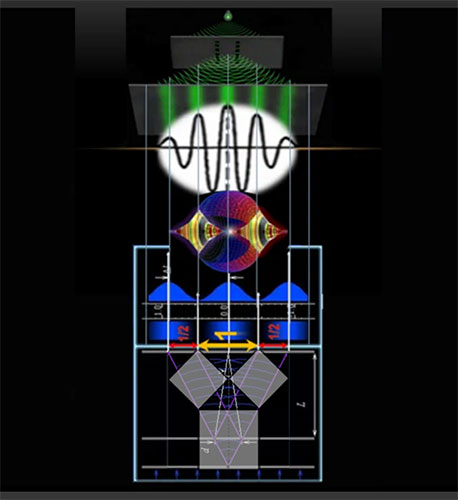
В материале, посвященном стоячим волнам, я уже говорил о том, что стоячие волны возникают в процессе наложения бегущей и отраженной гармонических волн.
Стоит отметить, что природа волновых процессов здесь роли абсолютно не играет. Это могут быть механические волны в упругой среде, электромагнитные волны (в частности, свет) в прозрачной среде или, например, в вакууме. И даже, как в нашем случае, ценовые волны, возникающие на графиках финансовых активов.
Но несмотря на такие, казалось бы, кардинальные различия в природе волн, ключевым понятием здесь по-прежнему выступает принцип суперпозиции, о котором я рассказывал ранее.
Суть принципа суперпозиции заключается в том, что если две гармонические волны накладываются друг на друга в определенной точке или области пространства, то они порождают новый волновой процесс.
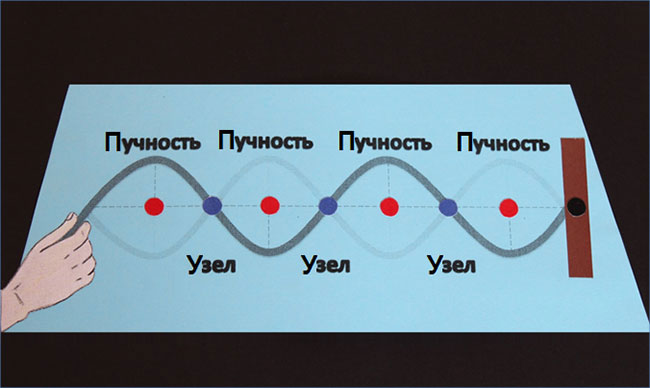
При этом значение колеблющейся совокупной волны всегда будет равно сумме соответствующих величин испущенной и отраженной волн по отдельности. Таким образом, стоячую волну можно рассматривать как суперпозицию бегущей и отраженной гармонических волн.
Однако если мы будем говорить не о стоячих волнах, образующихся в результате сложения бегущей и отраженной гармонических волн, а о суперпозиции двух отдельных точечных источников волн, то для описания понятия интерференции нам понадобится определение когерентности.
Просто когда речь идет о суперпозиции испущенной и отраженной волн (допустим, в струнах), они по умолчанию получаются когерентными из-за условия гармоничности.
КОГЕРЕНТНЫЕ ИСТОЧНИКИДопустим, у нас имеются два точечных источника, создающие волны в окружающем пространстве.

Если при этом частота колебаний этих источников (частота волн) одинакова и разность фаз колебаний с течением времени не меняется, то такие источники волн называются когерентными. Складываясь друг с другом, когерентные волны способны интерферировать.
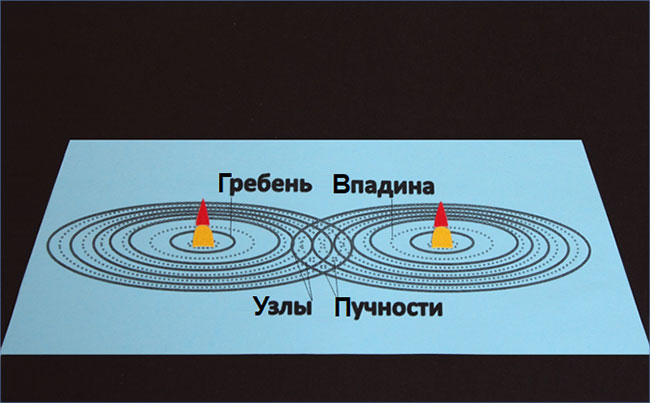
Интерференция волн – сложение когерентных волн с образованием устойчивой картины максимумов и минимумов амплитуды колебаний. На примере ниже мы видим, что в тех точках среды, где гребни волн складываются со впадинами, образуются узлы (стоячих волн), называемые минимумами интерференции:
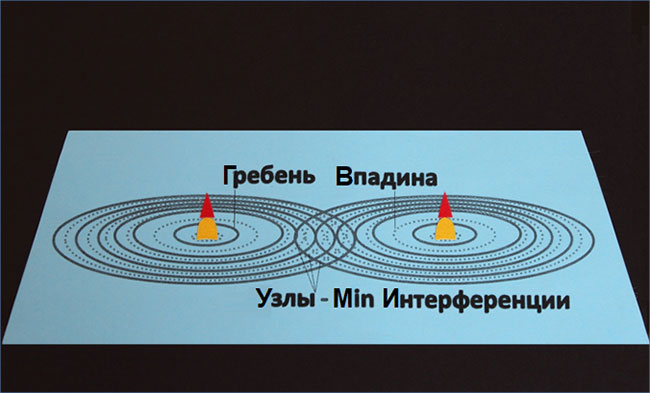
В тех же точках среды, где происходит сложение «гребень плюс гребень» либо «впадина плюс впадина», образуются пучности (стоячих волн), или максимумы интерференции:
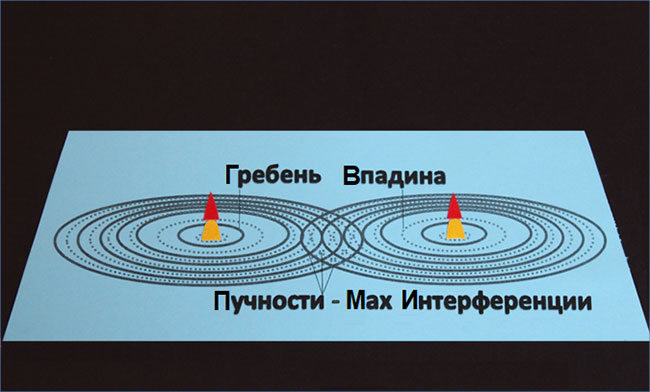
Итак, рассмотрим два источника когерентных волн S1 и S2.
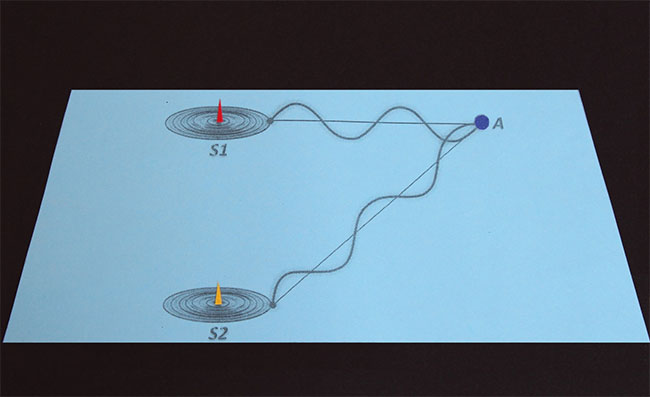
Для простоты считаем, что источники излучают волны одинаковой амплитуды, а разность фаз между источниками равна 0. Другими словами, предположим, что эти точечные источники являются точными копиями друг друга.
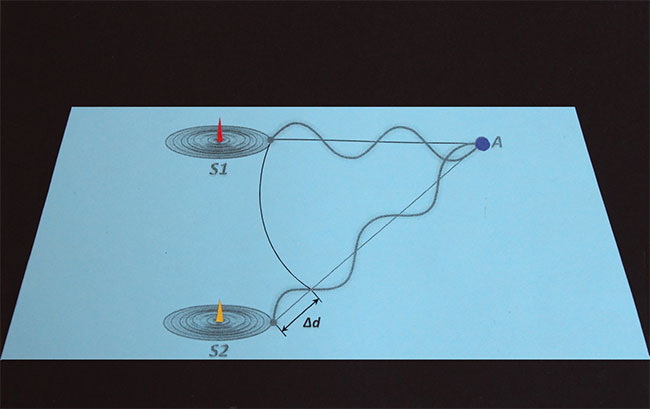
Теперь выберем некоторую произвольную точку А, в которой будем фиксировать наложение волн, испущенных источниками S1 и S2.
Очевидно, что результат интерференции (наложения волн) в этой точке будет зависеть от разности хода волн, которую обозначим как дельта d (Δd). Предположим, что разность хода (Δd) равна половине длины волны (λ/2):
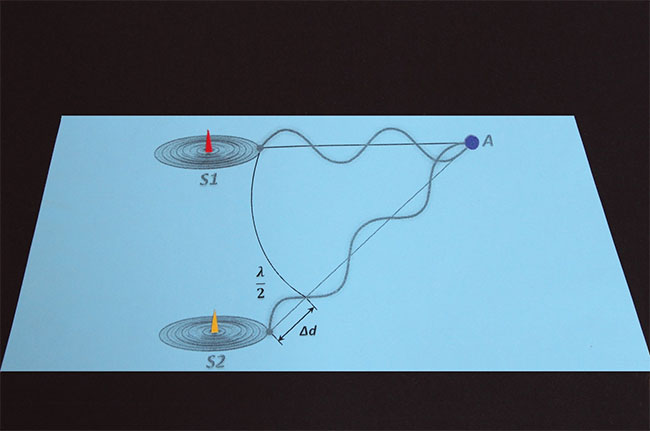
Тогда в точку А волны придут в противофазе, то есть гребень источника S2 придется на впадину источника S1. В результате такого наложения волн произойдет их ослабление друг другом и в точке А образуется интерференционный минимум (узел стоячей волны).
Очевидно, что этот результат будет только при условии, когда Δd = 1/2, 3/2, 5/2, …n и т. д. длины волны (лямбда):
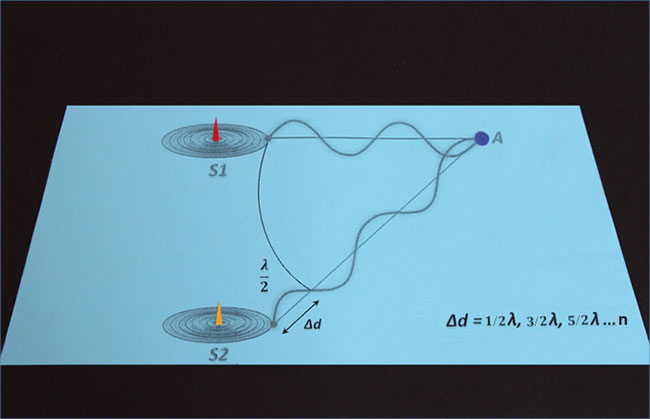
Тогда условие минимума интерференции (где k – возрастающий коэффициент) будет следующим:
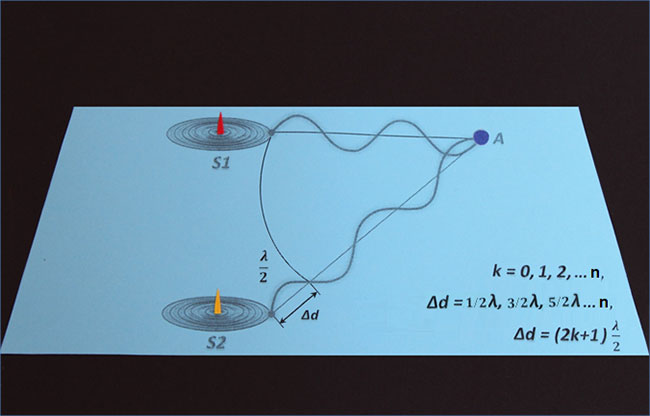
Другими словами, амплитуда колебаний в данной точке минимальна, если разность хода двух волн равна нечетному числу полуволн.
Если разность хода (Δd) равна одной длине волны (лямбда), тогда в точку А волны придут в одинаковой фазе, то есть впадина источника S2 придется на впадину источника S1, или, наоборот, гребень источника S2 придется на гребень источника S1. В этом случае образуется интерференционный максимум (пучность стоячей волны), характеризующийся усилением результирующей волны:
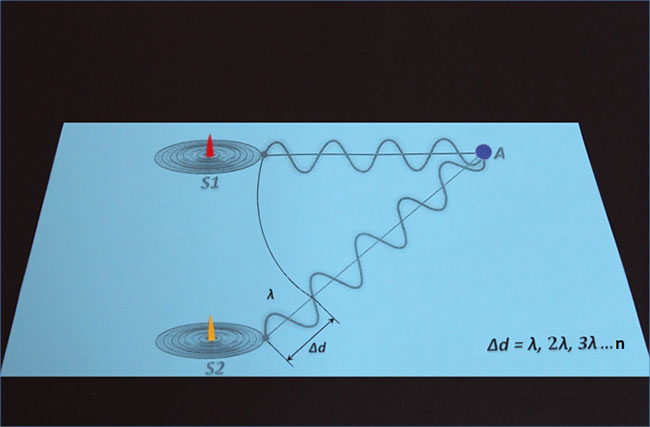
При этом очевидно, что результат будет одинаковым, если Δd = 1, 2, 3, … n и т. д. длины волны (лямбда):
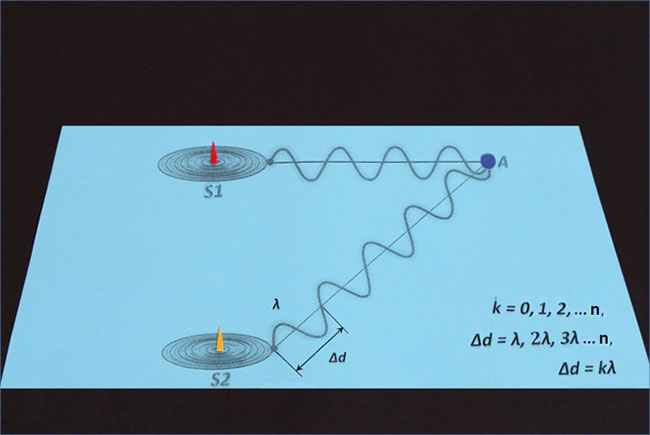
Тогда условие максимума интерференции, то есть амплитуда колебаний в данной точке максимальна, если разность хода равна целому числу волн, или можно сказать по-другому: когда разность хода равна четному числу полуволн.
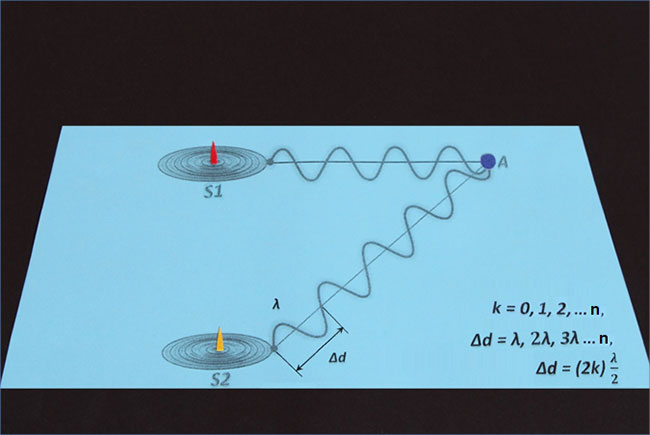
Теперь давайте подытожим.
1. Интерференционные минимумы возникают, когда разность хода равна нечетному количеству полуволн.
2. Интерференционные максимумы образуются, если разность хода равна четному количеству полуволн.
Вот почему в альтернативном волновом анализе играет большую роль понятие четности и нечетности. Они имеют непосредственное отношение к интерференционной картине среды, в нашем случае рынка.
Поэтому выделение волновых циклов можно сравнить с анализом интерференционной картины рынка, которая постоянно изменяется по мере возникновения новых волновых моделей, выступающих в роли своеобразных источников когерентных волн.
При этом пучности стоячих волн (циклы и полуциклы) будут соответствовать максимумам интерференции, а узлы стоячих волн (дробные циклы) будут соответствовать минимумам интерференции.
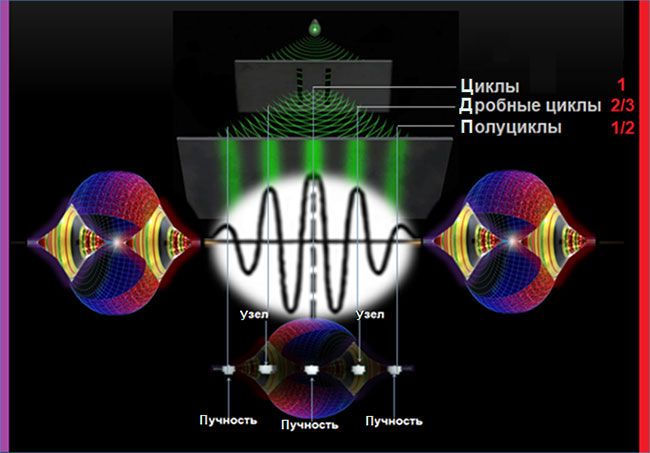
Кроме этого, в AWA используется аналогия между ценовым графиком и водным потоком.

Изображение сгенерировано нейросетью «Шедеврум»
Все дело в интерференции стоячих волн, которые проявляются, как известно, в любых средах.
Смотрите сами: на реках стоячие волны – это валы. На ценовых графиках стоячие волны – это циклы. На реках области турбулентности называются бочками, в альтернативном волновом анализе им соответствуют дробные циклы. Ну а форма рельефа русла (пороги, перекаты и т. д.) есть не что иное, как полуциклы. В общем, суть у них одна и та же.
Все они представляют собой своеобразные преграды на пути движения потока. Поэтому их необходимо преодолеть, чтобы у него была возможность двигаться далее.
В общем, такая аналогия позволяет не только запомнить непростые названия основных комбинаций пар, которые фиксируются в волновом балансе, а затем переносятся в таблицу учета циклов, но и получить общее представление о том, в каком месте ценового русла мы находимся в текущий момент.
Обо всем этом мы и будем говорить далее.
Закон Бернулли и режимы течения жидкости
Но для начала давайте вспомним такой важный закон гидродинамики, как закон Бернулли.
Закон Бернулли устанавливает зависимость между скоростью потока жидкости и ее давлением. Согласно этому закону, если вдоль линии тока давление жидкости повышается, то скорость течения убывает, и наоборот.

Для стационарного течения несжимаемой жидкости уравнение Бернулли может быть получено как следствие закона сохранения энергии. Закон Бернулли утверждает, что
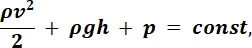
где ρ – плотность жидкости;
v – скорость потока;
h – высота;
p – давление;
g – ускорение свободного падения;
Константа в правой части иногда называется полным давлением, или весовым давлением. Она может менять значение для различных линий тока.
Если посмотреть на формулу внимательно, можно заметить, что размерность всех слагаемых – это единица энергии в единице объема.
Первое и второе слагаемые уравнения Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объема жидкости.
Третье слагаемое по своему смыслу является работой сил давления, но в гидравлике это слагаемое может называться энергией давления и представляет собой часть потенциальной энергии.
Таким образом, если вернуться к самому закону, который гласит, что если давление жидкости повышается, то скорость течения убывает, и наоборот, можно сделать вывод, что в случае роста давления происходит переход энергии из кинетической в потенциальную. А в случае увеличения скорости течения осуществляется, наоборот, переход энергии из потенциальной в кинетическую.
Такие переходы одного вида энергии в другой и наоборот очень сильно напоминают поведение стоячей волны, которая, как известно, не переносит энергию, а сохраняет ее низменной.
Дважды за период у стоячих волн происходит превращение энергии то полностью в потенциальную, сосредоточенную в основном вблизи узлов волны, то полностью в кинетическую, сосредоточенную в основном вблизи пучностей волны.
Однако вернемся к гидродинамике.
Как я уже говорил, в AWA используется аналогия между ценовым графиком и движением жидкости, например течением воды в руслах рек.
Именно поэтому применяется очень много терминологии из рафтинга (рафтинг – это сплав по рекам или искусственным каналам на большой надувной лодке, название которой и дало имя этому занятию), а также частично использованы названия из гидродинамики.
Кстати, рассматривая как-то на досуге такой раздел гидродинамики, как режимы течения жидкости, число Рейнольдса, я вдруг нашел для себя интересным выделить те участки движения водного потока, где происходит возникновение турбулентности (завихрений).
Опыты по этому вопросу были проведены английским ученым Осборном Рейнольдсом в 1883 г. Но давайте по порядку.
Итак, согласно законам гидродинамики, существует два основных режима течения жидкости:
• Ламинарное течение – процесс, при котором жидкость или газ перемещаются слоями без перемешивания и пульсаций (нет беспорядочных быстрых изменений скорости и давления). Характеризуется слоистым характером течения жидкости, отсутствием перемешивания, неизменностью давления и скорости во времени.
• Турбулентное течение – процесс, когда при увеличении скорости течения жидкости или газа образуются нелинейные фрактальные волны. При этом происходит вихреобразование с вращательным движением жидкости, возникают непрерывные пульсации давления и скорости в потоке воды.
Кстати, обратите внимание на фразу «возникают непрерывные пульсации давления и скорости в потоке воды». То есть переход потенциальной энергии в кинетическую энергию и наоборот. Все в точности как у стоячих волн.
А так как в AWA движение цены рассматривается как своеобразный вихревой поток, нас будут интересовать только режимы турбулентного течения жидкости.
РЕЖИМ ТУРБУЛЕНТНОГО ТЕЧЕНИЯ ЖИДКОСТИ ПРИ РАСШИРЕНИИ ПОТОКАСогласно исследованиям Рейнольдса, при внезапном расширении русла происходит потеря напора – энергии, которая расходуется на вихреобразование, связанное с отрывом потока от стенок, то есть на поддержание вращательного движения жидкости.

Области вихреобразования здесь и далее на рисунках обозначены завитками.
Аналогичная ситуация происходит с течением турбулентной жидкости при плавном расширении русла. Такое расширение называется диффузор.

В диффузоре, как и при внезапном расширении русла, происходит отрыв основного потока от стенки русла и наблюдается вихреобразование.
Таким образом, течение жидкости при расширении потока сопровождается уменьшением скорости движения и увеличением давления, то есть преобразованием кинетической энергии движения жидкости в потенциальную энергию давления.
РЕЖИМ ТУРБУЛЕНТНОГО ТЕЧЕНИЯ ЖИДКОСТИ ПРИ СУЖЕНИИ ПОТОКАПри внезапном сужении русла происходит потеря напора – энергии, которая расходуется на трение потока при входе в более узкую трубу и потери на вихреобразование, связанное с отрывом потока от стенок и образующееся вокруг суженой части потока.

Аналогичная ситуация происходит с течением турбулентной жидкости при плавном сужении русла. Такое сужение называется конфузор.
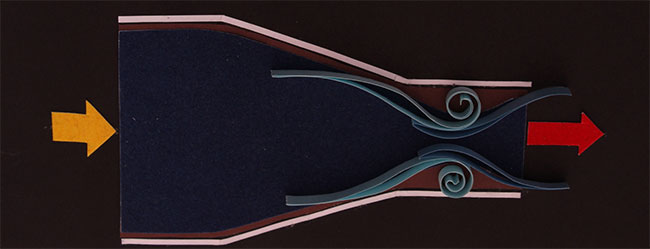
В результате этого образуются зоны вихреобразования, которые возникают в кольцевом пространстве вокруг суженной части потока.
Таким образом, при сужении русла происходит увеличение скорости движения потока и снижение давления, то есть преобразование потенциальной энергии давления в кинетическую энергию движения жидкости.
Теперь, если мы применим эту теорию к рафтингу, то увидим, что те же самые законы действуют и на реках. Такие области вихреобразования (циркуляции) в рафтинге называются улово.
Улово – участок реки, где основной поток отрывается от берегов русла, в результате чего возникает противоток основному течению либо возникает водоворот. Чаще всего это возникает у прижимов, вблизи перекатов, выступов берега, в местах резкого расширения или после сужения русла реки, впадения притоков и т. д.
Если мы внимательно посмотрим на пример течения жидкости в условия сужения русла, можно выделить ряд интересных особенностей поведения турбулентного потока.
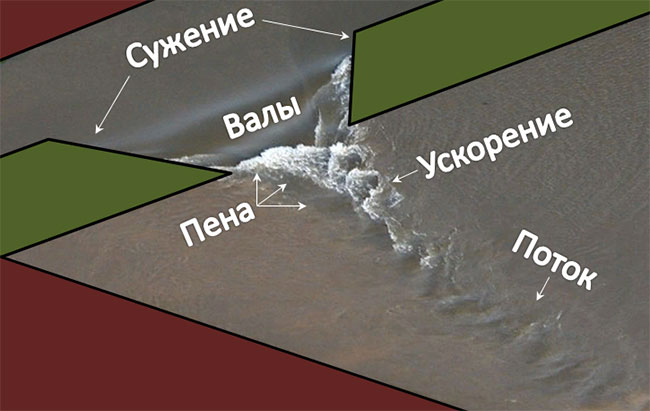
Очень часто зоны вихреобразования (циркуляции) возникают сразу после суженной части потока, проявляясь в виде пены по краям основного течения.
Обратите внимание на светлые области пенообразования, а именно на то, где расположены эти участки. Правильно: зона вихреобразования (циркуляции) образуется сразу после суженной части потока, в момент его максимального ускорения.
Затем по мере снижения скорости потока пена исчезает, и остается только струя. Таким образом, именно резкое ускорение (или замедление) потока и порождает области циркуляции. Это области образования поверхностных бочек (R/2, R/3, R/4).
Динамика водного потока. Виды препятствий
Я уже говорил о том, что использую аналогию между ценовым графиком и рекой.
На реках стоячие волны – это валы. На ценовых графиках стоячие волны – это циклы.
На реках области турбулентности – это бочки, в альтернативном волновом анализе им соответствуют дробные циклы. Ну а форма рельефа русла реки (пороги, перекаты и т. д.) – это полуциклы.
Поэтому я решил использовать терминологию из лекций по рафтингу, чтобы можно было подробно классифицировать все существующие волновые препятствия.
А начнем мы с камней. Да-да, с тех самых камней, которые встречаются в руслах рек.
КАМЕНЬ
Изображение сгенерировано нейросетью «Шедеврум»
В AWA камнями называются волновые препятствия, которые имеют параметр интерференции 1.
Камни представляют собой одну из разновидностей препятствий, которые могут встречаться на пути водного потока.

