Curious Myths of the Middle Ages

Then Tanhäuser, full of despair, and with his soul darkened, went away, and returned to the only asylum open to him, the Venusberg. But lo! three days after he had gone, Urban discovered that his pastoral staff had put forth buds, and had burst into flower. Then he sent messengers after Tanhäuser, and they reached the Hörsel vale to hear that a wayworn man, with haggard brow and bowed head, had just entered the Hörselloch. Since then Tanhäuser has not been seen.

Such is the sad yet beautiful story of Tanhäuser. It is a very ancient myth Christianized, a wide-spread tradition localized. Originally heathen, it has been transformed, and has acquired new beauty by an infusion of Christianity. Scattered over Europe, it exists in various forms, but in none so graceful as that attached to the Hörselberg. There are, however, other Venusbergs in Germany; as, for instance, in Swabia, near Waldsee; another near Ufhausen, at no great distance from Freiburg (the same story is told of this Venusberg as of the Hörselberg); in Saxony there is a Venusberg not far from Wolkenstein. Paracelsus speaks of a Venusberg in Italy, referring to that in which Æneas Sylvius (Ep. 16) says Venus or a Sibyl resides, occupying a cavern, and assuming once a week the form of a serpent. Geiler v. Keysersperg, a quaint old preacher of the fifteenth century, speaks of the witches assembling on the Venusberg.

The story, either in prose or verse, has often been printed. Some of the earliest editions are the following: —

“Das Lied von dem Danhewser.” Nürnberg, without date; the same, Nürnberg, 1515. – “Das Lyedt v. d. Thanheuser.” Leyptzk, 1520. – “Das Lied v. d. Danheüser,” reprinted by Bechstein, 1835. – “Das Lied vom edlen Tanheuser, Mons Veneris.” Frankfort, 1614; Leipzig, 1668. – “Twe lede volgen Dat erste vain Danhüsser.” Without date. – “Van heer Danielken.” Tantwerpen, 1544. – A Danish version in “Nyerup, Danske Viser,” No. VIII.

Let us now see some of the forms which this remarkable myth assumed in other countries. Every popular tale has its root, a root which may be traced among different countries, and though the accidents of the story may vary, yet the substance remains unaltered. It has been said that the common people never invent new story-radicals any more than we invent new word-roots; and this is perfectly true. The same story-root remains, but it is varied according to the temperament of the narrator or the exigencies of localization. The story-root of the Venusberg is this: —

The underground folk seek union with human beings.

α. A man is enticed into their abode, where he unites with a woman of the underground race.

β. He desires to revisit the earth, and escapes.

γ. He returns again to the region below.

Now, there is scarcely a collection of folk-lore which does not contain a story founded on this root. It appears in every branch of the Aryan family, and examples might be quoted from Modern Greek, Albanian, Neapolitan, French, German, Danish, Norwegian and Swedish, Icelandic, Scotch, Welsh, and other collections of popular tales. I have only space to mention some.

There is a Norse Tháttr of a certain Helgi Thorir’s son, which is, in its present form, a production of the fourteenth century. Helgi and his brother Thorstein went on a cruise to Finnmark, or Lapland. They reached a ness, and found the land covered with forest. Helgi explored this forest, and lighted suddenly on a party of red-dressed women riding upon red horses. These ladies were beautiful and of troll race. One surpassed the others in beauty, and she was their mistress. They erected a tent and prepared a feast. Helgi observed that all their vessels were of silver and gold. The lady, who named herself Ingibjorg, advanced towards the Norseman, and invited him to live with her. He feasted and lived with the trolls for three days, and then returned to his ship, bringing with him two chests of silver and gold, which Ingibjorg had given him. He had been forbidden to mention where he had been and with whom; so he told no one whence he had obtained the chests. The ships sailed, and he returned home.

One winter’s night Helgi was fetched away from home, in the midst of a furious storm, by two mysterious horsemen, and no one was able to ascertain for many years what had become of him, till the prayers of the king, Olaf, obtained his release, and then he was restored to his father and brother, but he was thenceforth blind. All the time of his absence he had been with the red-vested lady in her mysterious abode of Glœsisvellir.

The Scotch story of Thomas of Ercildoune is the same story. Thomas met with a strange lady, of elfin race, beneath Eildon Tree, who led him into the underground land, where he remained with her for seven years. He then returned to earth, still, however, remaining bound to come to his royal mistress whenever she should summon him. Accordingly, while Thomas was making merry with his friends in the Tower of Ercildoune, a person came running in, and told, with marks of fear and astonishment, that a hart and a hind had left the neighboring forest, and were parading the street of the village. Thomas instantly arose, left his house, and followed the animals into the forest, from which he never returned. According to popular belief, he still “drees his weird” in Fairy Land, and is one day expected to revisit earth. (Scott, “Minstrelsy of the Scottish Border.”) Compare with this the ancient ballad of Tamlane.

Debes relates that “it happened a good while since, when the burghers of Bergen had the commerce of the Faroe Isles, that there was a man in Serraade, called Jonas Soideman, who was kept by the spirits in a mountain during the space of seven years, and at length came out, but lived afterwards in great distress and fear, lest they should again take him away; wherefore people were obliged to watch him in the night.” The same author mentions another young man who had been carried away, and after his return was removed a second time, upon the eve of his marriage.

Gervase of Tilbury says that “in Catalonia there is a lofty mountain, named Cavagum, at the foot of which runs a river with golden sands, in the vicinity of which there are likewise silver mines. This mountain is steep, and almost inaccessible. On its top, which is always covered with ice and snow, is a black and bottomless lake, into which if a stone be cast, a tempest suddenly arises; and near this lake is the portal of the palace of demons.” He then tells how a young damsel was spirited in there, and spent seven years with the mountain spirits. On her return to earth she was thin and withered, with wandering eyes, and almost bereft of understanding.

A Swedish story is to this effect. A young man was on his way to his bride, when he was allured into a mountain by a beautiful elfin woman. With her he lived forty years, which passed as an hour; on his return to earth all his old friends and relations were dead, or had forgotten him, and finding no rest there, he returned to his mountain elf-land.

In Pomerania, a laborer’s son, Jacob Dietrich of Rambin, was enticed away in the same manner.

There is a curious story told by Fordun in his “Scotichronicon,” which has some interest in connection with the legend of the Tanhäuser. He relates that in the year 1050, a youth of noble birth had been married in Rome, and during the nuptial feast, being engaged in a game of ball, he took off his wedding-ring, and placed it on the finger of a statue of Venus. When he wished to resume it, he found that the stony hand had become clinched, so that it was impossible to remove the ring. Thenceforth he was haunted by the Goddess Venus, who constantly whispered in his ear, “Embrace me; I am Venus, whom you have wedded; I will never restore your ring.” However, by the assistance of a priest, she was at length forced to give it up to its rightful owner.

The classic legend of Ulysses, held captive for eight years by the nymph Calypso in the Island of Ogygia, and again for one year by the enchantress Circe, contains the root of the same story of the Tanhäuser.

What may have been the significance of the primeval story-radical it is impossible for us now to ascertain; but the legend, as it shaped itself in the middle ages, is certainly indicative of the struggle between the new and the old faith.

We see thinly veiled in Tanhäuser the story of a man, Christian in name, but heathen at heart, allured by the attractions of paganism, which seems to satisfy his poetic instincts, and which gives full rein to his passions. But these excesses pall on him after a while, and the religion of sensuality leaves a great void in his breast.

He turns to Christianity, and at first it seems to promise all that he requires. But alas! he is repelled by its ministers. On all sides he is met by practice widely at variance with profession. Pride, worldliness, want of sympathy exist among those who should be the foremost to guide, sustain, and receive him. All the warm springs which gushed up in his broken heart are choked, his softened spirit is hardened again, and he returns in despair to bury his sorrows and drown his anxieties in the debauchery of his former creed.

A sad picture, but doubtless one very true.

Fatality of Numbers

THE laws governing numbers are so perplexing to the uncultivated mind, and the results arrived at by calculation are so astonishing, that it cannot be matter of surprise if superstition has attached itself to numbers.

But even to those who are instructed in numeration, there is much that is mysterious and unaccountable, much that only an advanced mathematician can explain to his own satisfaction. The neophyte sees the numbers obedient to certain laws; but why they obey these laws he cannot understand; and the fact of his not being able so to do, tends to give to numbers an atmosphere of mystery which impresses him with awe.

For instance, the property of the number 9, discovered, I believe, by W. Green, who died in 1794, is inexplicable to any one but a mathematician. The property to which I allude is this, that when 9 is multiplied by 2, by 3, by 4, by 5, by 6, &c., it will be found that the digits composing the product, when added together, give 9. Thus: —

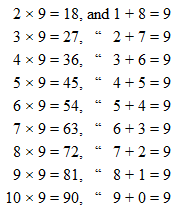
It will be noticed that 9 × 11 makes 99, the sum of the digits of which is 18 and not 9, but the sum of the digits 1 × 8 equals 9.

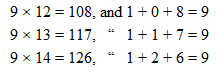
And so on to any extent.

M. de Maivan discovered another singular property of the same number. If the order of the digits expressing a number be changed, and this number be subtracted from the former, the remainder will be 9 or a multiple of 9, and, being a multiple, the sum of its digits will be 9.

For instance, take the number 21, reverse the digits, and you have 12; subtract 12 from 21, and the remainder is 9. Take 63, reverse the digits, and subtract 36 from 63; you have 27, a multiple of 9, and 2 + 7 = 9. Once more, the number 13 is the reverse of 31; the difference between these numbers is 18, or twice 9.

Again, the same property found in two numbers thus changed, is discovered in the same numbers raised to any power.

Take 21 and 12 again. The square of 21 is 441, and the square of 12 is 144; subtract 144 from 441, and the remainder is 297, a multiple of 9; besides, the digits expressing these powers added together give 9. The cube of 21 is 9261, and that of 12 is 1728; their difference is 7533, also a multiple of 9.

The number 37 has also somewhat remarkable properties; when multiplied by 3 or a multiple of 3 up to 27, it gives in the product three digits exactly similar. From the knowledge of this the multiplication of 37 is greatly facilitated, the method to be adopted being to multiply merely the first cipher of the multiplicand by the first multiplier; it is then unnecessary to proceed with the multiplication, it being sufficient to write twice to the right hand the cipher obtained, so that the same digit will stand in the unit, tens, and hundreds places.

For instance, take the results of the following table: —

The singular property of numbers the most different, when added, to produce the same sum, originated the use of magical squares for talismans. Although the reason may be accounted for mathematically, yet numerous authors have written concerning them, as though there were something “uncanny” about them. But the most remarkable and exhaustive treatise on the subject is that by a mathematician of Dijon, which is entitled “Traité complet des Carrés magiques, pairs et impairs, simple et composés, à Bordures, Compartiments, Croix, Chassis, Équerres, Bandes détachées, &c.; suivi d’un Traité des Cubes magiques et d’un Essai sur les Cercles magiques; par M. Violle, Géomètre, Chevalier de St. Louis, avec Atlas de 54 grandes Feuilles, comprenant 400 figures.” Paris, 1837. 2 vols. 8vo., the first of 593 pages, the second of 616. Price 36 fr.

I give three examples of magical squares: —

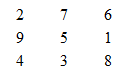
These nine ciphers are disposed in three horizontal lines; add the three ciphers of each line, and the sum is 15; add the three ciphers in each column, the sum is 15; add the three ciphers forming diagonals, and the sum is 15.

But the connection of certain numbers with the dogmas of religion was sufficient, besides their marvellous properties, to make superstition attach itself to them. Because there were thirteen at the table when the Last Supper was celebrated, and one of the number betrayed his Master, and then hung himself, it is looked upon through Christendom as unlucky to sit down thirteen at table, the consequence being that one of the number will die before the year is out. “When I see,” said Vouvenargues, “men of genius not daring to sit down thirteen at table, there is no error, ancient or modern, which astonishes me.”

Nine, having been consecrated by Buddhism, is regarded with great veneration by the Moguls and Chinese: the latter bow nine times on entering the presence of their Emperor.

Three is sacred among Brahminical and Christian people, because of the Trinity of the Godhead.

Pythagoras taught that each number had its own peculiar character, virtue, and properties.

“The unit, or the monad,” he says, “is the principle and the end of all; it is this sublime knot which binds together the chain of causes; it is the symbol of identity, of equality, of existence, of conservation, and of general harmony. Having no parts, the monad represents Divinity; it announces also order, peace, and tranquillity, which are founded on unity of sentiments; consequently One is a good principle.

“The number Two, or the dyad, the origin of contrasts, is the symbol of diversity, or inequality, of division and of separation. Two is accordingly an evil principle, a number of bad augury, characterizing disorder, confusion, and change.

“Three, or the triad, is the first of unequals; it is the number containing the most sublime mysteries, for everything is composed of three substances; it represents God, the soul of the world, the spirit of man.” This number, which plays so great a part in the traditions of Asia, and in the Platonic philosophy, is the image of the attributes of God.

“Four, or the tetrad, as the first mathematical power, is also one of the chief elements; it represents the generating virtue, whence come all combinations; it is the most perfect of numbers; it is the root of all things. It is holy by nature, since it constitutes the Divine essence, by recalling His unity, His power, His goodness, and His wisdom, the four perfections which especially characterize God. Consequently, Pythagoricians swear by the quaternary number, which gives the human soul its eternal nature.

“The number Five, or the pentad, has a peculiar force in sacred expiations; it is everything; it stops the power of poisons, and is redoubted by evil spirits.

“The number Six, or the hexad, is a fortunate number, and it derives its merit from the first sculptors having divided the face into six portions; but, according to the Chaldeans, the reason is, because God created the world in six days.

“Seven, or the heptad, is a number very powerful for good or for evil. It belongs especially to sacred things.

“The number Eight, or the octad, is the first cube, that is to say, squared in all senses, as a die, proceeding from its base two, an even number; so is man four-square, or perfect.

“The number Nine, or the ennead, being the multiple of three, should be regarded as sacred.

“Finally, Ten, or the decad, is the measure of all, since it contains all the numeric relations and harmonies. As the reunion of the four first numbers, it plays an eminent part, since all the branches of science, all nomenclatures, emanate from, and retire into it.”

It is hardly necessary for me here to do more than mention the peculiar character given to different numbers by Christianity. One is the numeral indicating the Unity of the Godhead; Two points to the hypostatic union; Three to the Blessed Trinity; Four to the Evangelists; Five to the Sacred Wounds; Six is the number of sin; Seven that of the gifts of the Spirit; Eight, that of the Beatitudes; Ten is the number of the commandments; Eleven speaks of the Apostles after the loss of Judas; Twelve, of the complete apostolic college.

I shall now point out certain numbers which have been regarded with superstition, and certain events connected with numbers which are of curious interest.

The number 14 has often been observed as having singularly influenced the life of Henry IV. and other French princes. Let us take the history of Henry.

On the 14th May, 1029, the first king of France named Henry was consecrated, and on the 14th May, 1610, the last Henry was assassinated.

Fourteen letters enter into the composition of the name of Henri de Bourbon, who was the 14th king bearing the titles of France and Navarre.

The 14th December, 1553, that is, 14 centuries, 14 decades, and 14 years after the birth of Christ, Henry IV. was born; the ciphers of the date 1553, when added together, giving the number 14.

The 14th May, 1554, Henry II. ordered the enlargement of the Rue de la Ferronnerie. The circumstance of this order not having been carried out, occasioned the murder of Henry IV. in that street, four times 14 years after.

The 14th May, 1552, was the date of the birth of Marguérite de Valois, first wife of Henry IV.

On the 14th May, 1588, the Parisians revolted against Henry III., at the instigation of the Duke of Guise.

On the 14th March, 1590, Henry IV. gained the battle of Ivry.

On the 14th May, 1590, Henry was repulsed from the Fauxbourgs of Paris.

On the 14th November, 1590, the Sixteen took oath to die rather than serve Henry.

On the 14th November, 1592, the Parliament registered the Papal Bull giving power to the legate to nominate a king to the exclusion of Henry.

On the 14th December, 1599, the Duke of Savoy was reconciled to Henry IV.

On the 14th September, 1606, the Dauphin, afterwards Louis XIII., was baptized.

On the 14th May, 1610, the king was stopped in the Rue de la Ferronnerie, by his carriage becoming locked with a cart, on account of the narrowness of the street. Ravaillac took advantage of the occasion for stabbing him.

Henry IV. lived four times 14 years, 14 weeks, and four times 14 days; that is to say, 56 years and 5 months.

On the 14th May, 1643, died Louis XIII., son of Henry IV.; not only on the same day of the same month as his father, but the date, 1643, when its ciphers are added together, gives the number 14, just as the ciphers of the date of the birth of his father gave 14.

Louis XIV. mounted the throne in 1643: 1 + 6 + 4 + 3 = 14.

He died in the year 1715: 1 + 7 + 1 + 5 = 14.

He lived 77 years, and 7 + 7 = 14.

Louis XV. mounted the throne in the same year; he died in 1774, which also bears the stamp of 14, the extremes being 14, and the sum of the means 7 + 7 making 14.

Louis XVI. had reigned 14 years when he convoked the States General, which was to bring about the Revolution.

The number of years between the assassination of Henry IV. and the dethronement of Louis XVI. is divisible by 14.

Louis XVII. died in 1794; the extreme digits of the date are 14, and the first two give his number.

The restoration of the Bourbons took place in 1814, also marked by the extremes being 14; also by the sum of the ciphers making 14.

The following are other curious calculations made respecting certain French kings.

Add the ciphers composing the year of the birth or of the death of some of the kings of the third race, and the result of each sum is the titular number of each prince. Thus: —

Louis IX. was born in 1215; add the four ciphers of this date, and you have IX.

Charles VII. was born in 1402; the sum of 1 + 4 + 2 gives VII.

Louis XII. was born in 1461; and 1 + 4 + 6 + 1 = XII.

Henry IV. died in 1610; and 1 + 6 + 1 = twice IV.

Louis XIV. was crowned in 1643; and these four ciphers give XIV. The same king died in 1715; and this date gives also XIV. He was aged 77 years, and again 7 + 7 = 14.

Louis XVIII. was born in 1755; add the digits, and you have XVIII.

What is remarkable is, that this number 18 is double the number of the king to whom the law first applies, and is triple the number of the kings to whom it has applied.

Here is another curious calculation: —

Robespierre fell in 1794;

Napoleon in 1815, and Charles X. in 1830.

Now, the remarkable fact in connection with these dates is, that the sum of the digits composing them, added to the dates, gives the date of the fall of the successor. Robespierre fell in 1794; 1 + 7 + 9 + 4 = 21, 1794 + 21 = 1815, the date of the fall of Napoleon; 1 + 8 + 1 + 5 = 15, and 1815 + 15 = 1830, the date of the fall of Charles X.

There is a singular rule which has been supposed to determine the length of the reigning Pope’s life, in the earlier half of a century. Add his number to that of his predecessor, to that add ten, and the result gives the year of his death.

Pius VII. succeeded Pius VI.; 6 + 7 = 13; add 10, and the sum is 23. Pius VII. died in 1823.

Leo XII. succeeded Pius VII.; 12 + 7 + 10 = 29; and Leo XII. died in 1829.

Pius VIII. succeeded Leo XII.; 8 + 12 + 10 = 30; and Pius VIII. died in 1830.

However, this calculation does not always apply.

Gregory XVI. ought to have died in 1834, but he did not actually vacate his see till 1846.

It is also well known that an ancient tradition forbids the hope of any of St. Peter’s successors, pervenire ad annos Petri; i. e., to reign 25 years.

Those who sat longest are

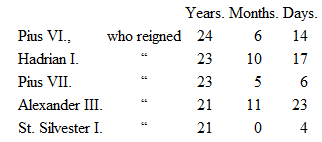
There is one numerical curiosity of a very remarkable character, which I must not omit.

The ancient Chamber of Deputies, such as it existed in 1830, was composed of 402 members, and was divided into two parties. The one, numbering 221 members, declared itself strongly for the revolution of July; the other party, numbering 181, did not favor a change. The result was the constitutional monarchy, which re-established order after the three memorable days of July. The parties were known by the following nicknames. The larger was commonly called La queue de Robespierre, and the smaller, Les honnêtes gens. Now, the remarkable fact is, that if we give to the letters of the alphabet their numerical values as they stand in their order, as 1 for A, 2 for B, 3 for C, and so on to Z, which is valued at 25, and then write vertically on the left hand the words, La queue de Robespierre, with the number equivalent to each letter opposite to it, and on the right hand, in like manner, Les honnêtes gens, if each column of numbers be summed up, the result is the number of members who formed each party.