Time and Tide: A Romance of the Moon

Thus we see that the moon is endowed with two sources of energy, one of which is due to its separation from the earth, and the other to the speed of its motion. Though these are distinct, they are connected together by a link which it is important for us to comprehend. The speed with which the moon revolves around the earth is connected with the moon's distance from the earth. The moon might, for instance, revolve in a larger circle than that which it actually pursues; but if it did so, the speed of its motion would have to be appropriately lessened. The orbit of the moon might have a much smaller radius than it has at present, provided that the speed was sufficiently increased to compensate for the increased attraction which the earth would exercise at the lessened distance. Indeed, I am here only stating what every one is familiar with under the form of Kepler's Law, that the square of the periodic time is in proportion to the cube of the mean distance. To each distance of the moon therefore belongs an appropriate speed. The energy due to the moon's position and the energy due to its motion are therefore connected together. One of these quantities cannot be altered without the other undergoing change. If the moon's orbit were increased there would be a gain of energy due to the enlarged distance, and a loss of energy due to the diminished speed. These would not, however, exactly compensate. On the whole, we may represent the total energy of the moon as a single quantity, which increases when the distance of the moon from the earth increases, and lessens when the distance from the earth to the moon lessens. For simplicity we may speak of this as moon-energy.

But the most important constituent of the store of energy in the earth-moon system is that contributed by the earth itself. I do not now speak of the energy due to the velocity of the earth in its orbit round the sun. The moon indeed participates in this equally with the earth, but it does not affect those mutual actions between the earth and moon with which we are at present concerned. We are, in fact, discussing the action of that piece of machinery the earth-moon system; and its action is not affected by the circumstance that the entire machine is being bodily transported around the sun in a great annual voyage. This has little more to do with the action of our present argument than has the fact that a man is walking about to do with the motions of the works of the watch in his pocket. We shall, however, have to allude to this subject further on.

The energy of the earth which is significant in the earth-moon theory is due to the earth's rotation upon its axis. We may here again use as an illustration the action of machinery; and the special contrivance that I now refer to is the punching-engine that is used in our ship-building works. In preparing a plate of iron to be riveted to the side of a ship, a number of holes have to be made all round the margin of the plate. These holes must be half an inch or more in diameter, and the plate is sometimes as much as, or more than, half an inch in thickness. The holes are produced in the metal by forcing a steel punch through it; and this is accomplished without even heating the plate so as to soften the iron. It is needless to say that an intense force must be applied to the punch. On the other hand, the distance through which the punch has to be moved is comparatively small. The punch is attached to the end of a powerful lever, the other end of the lever is raised by a cam, so as to depress the punch to do its work. An essential part of the machine is a small but heavy fly-wheel connected by gearing with the cam.

This fly-wheel when rapidly revolving contains within it, in virtue of its motion, a large store of energy which has gradually accumulated during the time that the punch is not actually in action. The energy is no doubt originally supplied from a steam-engine. What we are especially concerned with is the action of the rapidly rotating wheel as a reservoir in which a large store of energy can be conveniently maintained until such time as it is wanted. In the action of punching, when the steel die comes down upon the surface of the plate, a large quantity of energy is suddenly demanded to force the punch against the intense resistance it experiences; the energy for this purpose is drawn from the store in the fly-wheel, which experiences no doubt a check in its velocity, to be regained again from the energy of the engine during the interval which elapses before the punch is called on to make the next hole.

Another illustration of the fly-wheel on a splendid scale is seen in our mighty steel works, where ponderous rails are being manufactured. A white-hot ingot of steel is presented to a pair of powerful rollers, which grip the steel, and send it through at the other side both compressed and elongated. Tremendous power is required to meet the sudden demand on the machine at the critical moment. To obtain this power an engine of stupendous proportions is sometimes attached directly to the rollers, but more frequently an engine of rather less horse-power will be used, the might of this engine being applied to giving rapid rotation to an immense fly-wheel, which may thus be regarded as a reservoir full of energy. The rolling mills then obtain from this store in the fly-wheel whatever energy is necessary for their gigantic task.

These illustrations will suffice to show how a rapidly rotating body may contain energy in virtue of its rotation, just as a cannon-ball contains energy in virtue of its speed of translation, or as a clock-weight has energy in virtue of the fact that it has some distance to fall before it reaches the earth. The rotating body need not necessarily have the shape of a wheel—it may be globular in form; nor need the axes of rotation be fixed in bearings, like those of the fly-wheel; nor of course is there any limit to the dimensions which the rotating body may assume. Our earth is, in fact, a vast rotating body 8000 miles in diameter, and turning round upon its axis once every twenty-three hours and fifty-six minutes. Viewed in this way, the earth is to be regarded as a gigantic fly-wheel containing a quantity of energy great in correspondence with the earth's mass. The amount of energy which can be stored by rotation also depends upon the square of the velocity with which the body turns round; thus if our earth turned round in half the time which it does at present, that is, if the day was twelve hours instead of twenty-four hours, the energy contained in virtue of that rotation would be four times its present amount.

Reverting now to the earth-moon system, the energy which that system contains consists essentially of two parts—the moon-energy, whose composite character I have already explained, and the earth-energy, which has its origin solely in the rotation of the earth on its axis. It is necessary to observe that these are essentially distinct—there is no necessary relation between the speed of the earth's rotation and the distance of the moon, such as there is between the distance of the moon and the speed with which it revolves in its orbit.

For completeness, it ought to be added that there is also some energy due to the moon's rotation on its axis, but this is very small for two reasons: first, because the moon is small compared with the earth, and second, because the angular velocity of the moon is also very small compared with that of the earth. We may therefore dismiss as insignificant the contributions from this source of energy to the sum total.

I have frequently used illustrations derived from machinery, but I want now to emphasize the profound distinction that exists between the rotation of the earth and the rotation of a fly-wheel in a machine shop. They are both, no doubt, energy-holders, but it must be borne in mind, that as the fly-wheel doles out its energy to supply the wants of the machines with which it is connected, a restitution of its store is continually going on by the action of the engine, so that on the whole the speed of the fly-wheel does not slacken. The earth, however, must be likened to a fly-wheel which has been disconnected with the engine. If, therefore, the earth have to supply certain demands on its accumulation of energy, it can only do so by a diminution of its hoard, and this involves a sacrifice of some of its speed.

In the earth-moon system there is no engine at hand to restore the losses of energy which are inevitable when work has to be done. But we have seen that work is done; we have shown, in fact, that the tides are at present doing work, and have been doing work for as long a period in the past as our imagination can extend to. The energy which this work has necessitated can only have been drawn from the existing store in the system; that energy consists of two parts—the moon-energy and the earth's rotation energy. The problem therefore for us to consider is, which of these two banks the tides have drawn on to meet their constant expenditure. This is not a question that can be decided offhand; in fact, if we attempt to decide it in an offhand manner we shall certainly go wrong. It seems so very plausible to say that as the moon causes the tides, therefore the energy which these tides expend should be contributed by the moon. But this is not the case. It actually happens that though the moon does cause the tides, yet when those tides consume energy they draw it not from the distant moon, but from the vast supply which they find ready to their hand, stored up in the rotation of the earth.

The demonstration of this is not a very simple matter; in fact, it is so far from being simple that many philosophers, including some eminent ones too, while admitting that of course the tides must have drawn their energy from one or other or both of these two sources, yet found themselves unable to assign how the demand was distributed between the two conceivable sources of supply.

We are indebted to Professor Purser of Belfast for having indicated the true dynamical principle on which the problem depends. It involves reasoning based simply on the laws of motion and on elementary mathematics, but not in the least involving questions of astronomical observation. It would be impossible for me in a lecture like this to give any explanation of the mathematical principles referred to. I shall, however, endeavour by some illustrations to set before you what this profound principle really is. Were I to give it the old name I should call it the law of the conservation of areas; the more modern writers, however, speak of it as the conservation of moment of momentum, an expression which exhibits the nature of the principle in a more definite manner.

I do not see how to give any very accurate illustration of what this law means, but I must make the attempt, and if you think the illustration beneath the dignity of the subject, I can only plead the difficulty of mathematics as an excuse. Let us suppose that a ball-room is fairly filled with dancers, or those willing to dance, and that a merry waltz is being played; the couples have formed, and the floor is occupied with pairs who are whirling round and round in that delightful amusement. Some couples drop out for a while and others strike in; the fewer couples there are the wider is the range around which they can waltz, the more numerous the couples the less individual range will they possess. I want you to realize that in the progress of the dance there is a certain total quantity of spin at any moment in progress; this spin is partly made up of the rotation by which each dancer revolves round his partner, and partly of the circular orbit about the room which each couple endeavours to describe. If there are too many couples on the floor for the general enjoyment of the dance, then both the orbit and the angular velocity of each couple will be restricted by the interference with their neighbours. We may, however, assert that so long as the dance is in full swing the total quantity of spin, partly rotational and partly orbital, will remain constant. When there are but few couples the unimpeded rotation and the large orbits will produce as much spin as when there is a much larger number of couples, for in the latter case the diminished freedom will lessen the quantity of spin produced by each individual pair. It will sometimes happen too that collision will take place, but the slight diversions thus arising only increase the general merriment, so that the total quantity of spin may be sustained, even though one or two couples are placed temporarily hors de combat. I have invoked a ball-room for the purpose of bringing out what we may call the law of the conservation of spin. No matter how much the individual performers may change, or no matter what vicissitudes arise from their collision and other mutual actions, yet the total quantity of spin remains unchanged.

Let us look at the earth-moon system. The law of the conservation of moment of momentum may, with sufficient accuracy for our present purpose, be interpreted to mean that the total quantity of spin in the system remains unaltered. In our system the spin is threefold; there is first the rotation of the earth on its axis, there is the rotation of the moon on its axis, and then there is the orbital revolution of the moon around the earth. The law to which we refer asserts that the total quantity of these three spins, each estimated in the proper way, will remain constant. It matters not that tides may ebb and flow, or that the distribution of the spin shall vary, but its total amount remains inflexibly constant. One constituent of the total amount—that is, the rotation of the moon on its axis—is so insignificant, that for our present purposes it may be entirely disregarded. We may therefore assert that the amount of spin in the earth, due to its rotation round its axis, added to the amount of spin in the moon due to its revolution round the earth, remains unalterable. If one of these quantities change by increase or by decrease, the other must correspondingly change by decrease or by increase. If, therefore, from any cause, the earth began to spin a little more quickly round its axis, the moon must do a little less spin; and consequently, it must shorten its distance from the earth. Or suppose that the earth's velocity of rotation is abated, then its contribution to the total amount of spin is lessened; the deficiency must therefore be made up by the moon, but this can only be done by an enlargement of the moon's orbit. I should add, as a caution, that these results are true only on the supposition that the earth-moon system is isolated from all external interference. With this proviso, however, it matters not what may happen to the earth or moon, or what influence one of them may exert upon the other, no matter what tides may be raised, no matter even if the earth fly into fragments, the whole quantity of spin of all those fragments would, if added to the spin of the moon, yield the same unalterable total. We are here in possession of a most valuable dynamical principle. We are not concerned with any special theory as to the action of the tides; it is sufficient for us that in some way or other the tides have been caused by the moon, and that being so, the principle of the conservation of spin will apply.

Were the earth and the moon both rigid bodies, then there could be of course no tides on the earth, it being rigid and devoid of ocean. The rotation of the earth on its axis would therefore be absolutely without change, and therefore the necessary condition of the conservation of spin would be very simply attained by the fact that neither of the constituent parts changed. The earth, however, not being entirely rigid, and being subject to tides, this simple state of things cannot continue; there must be some change in progress.

I have already shown that the fact of the ebbing and the flowing of the tide necessitates an expenditure of energy, and we saw that this energy must come either from that stored up in the earth by its rotation, or from that possessed by the moon in virtue of its distance and revolution. The law of the conservation of spin will enable us to decide at once as to whence the tides get their energy. Suppose they took it from the moon, the moon would then lose in energy, and consequently come nearer the earth. The quantity of spin contributed by the moon would therefore be lessened, and accordingly the spin to be made up by the earth would be increased. That means, of course, that the velocity of the earth rotating on its axis must be increased, and this again would necessitate an increase in the earth's rotational energy. It can be shown, too, that to keep the total spin right, the energy of the earth would have to gain more than the moon would have lost by revolving in a smaller orbit. Thus we find that the total quantity of energy in the system would be increased. This would lead to the absurd result that the action of the tides manufactured energy in our system. Of course, such a doctrine cannot be true; it would amount to a perpetual motion! We might as well try to get a steam-engine which would produce enough heat by friction not only to supply its own boilers, but to satisfy all the thermal wants of the whole parish. We must therefore adopt the other alternative. The tides do not draw their energy from the moon; they draw it from the store possessed by the earth in virtue of its rotation.

We can now state the end of this rather long discussion in a very simple and brief manner. Energy can only be yielded by the earth at the expense of some of the speed of its rotation. The tides must therefore cause the earth to revolve more slowly; in other words, the tides are increasing the length of the day.

The earth therefore loses some of its velocity of rotation; consequently it does less than its due share of the total quantity of spin, and an increased quantity of spin must therefore be accomplished by the moon; but this can only be done by an enlargement of its orbit. Thus there are two great consequences of the tides in the earth-moon system—the days are getting longer, the moon is receding further.

These points are so important that I shall try and illustrate them in another way, which will show, at all events, that one and both of these tidal phenomena commend themselves to our common sense. Have we not shown how the tides in their ebb and flow are incessantly producing friction, and have we not also likened the earth to a great wheel? When the driver wants to stop a railway train the brakes are put on, and the brake is merely a contrivance for applying friction to the circumference of a wheel for the purpose of checking its motion. Or when a great weight is being lowered by a crane, the motion is checked by a band which applies friction on the circumference of a wheel, arranged for the special purpose. Need we then be surprised that the friction of the tides acts like a brake on the earth, and gradually tends to check its mighty rotation? The progress of lengthening the day by the tides is thus readily intelligible. It is not quite so easy to see why the ebbing and the flowing of the tide on the earth should actually have the effect of making the moon to retreat; this phenomenon is in deference to a profound law of nature, which tells us that action and reaction are equal and opposite to each other. If I might venture on a very homely illustration, I may say that the moon, like a troublesome fellow, is constantly annoying the earth by dragging its waters backward and forward by means of tides; and the earth, to free itself from this irritating interference, tries to push off the aggressor and to make him move further away.

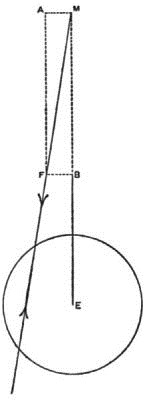
Fig. 2.

Another way in which we can illustrate the retreat of the moon as the inevitable consequence of tidal friction is shown in the adjoining figure, in which the large body E represents the earth, and the small body M the moon. We may for simplicity regard the moon as a point, and as this attracts each particle of the earth, the total effect of the moon on the earth may be represented by a single force. By the law of equality of action and reaction, the force of the earth on the moon is to be represented by an equal and opposite force. If there were no tides then the moon's force would of course pass through the earth's centre; but as the effect of the moon is to slacken the earth's rotation, it follows that the total force does not exactly pass through the line of the earth's centre, but a little to one side, in order to pull the opposite way to that in which the earth is turning, and thus bring down its speed. We may therefore decompose the earth's total force on the moon into two parts, one of which tends directly towards the earth's centre, while the other acts tangentially to the moon's orbit. The central force is of course the main guiding power which keeps the moon in its path; but the incessant tangential force constantly tends to send the moon out further and further, and thus the growth of its orbit can be accounted for.

We therefore conclude finally, that the tides are making the day longer and sending the moon away further. It is the development of the consequences of these laws that specially demands our attention in these lectures. We must have the courage to look at the facts unflinchingly, and deduce from them all the wondrous consequences they involve. Their potency arises from a characteristic feature—they are unintermitting. Most of the great astronomical changes with which we are ordinarily familiar are really periodic: they gradually increase in one direction for years, for centuries, or for untold ages; but then a change comes, and the increase is changed into a decrease, so that after the lapse of becoming periods the original state of things is restored. Such periodic phenomena abound in astronomy. There is the annual fluctuation of the seasons; there is the eighteen or nineteen year period of the moon; there is the great period of the precession of the equinoxes, amounting to twenty-six thousand years; and then there is the stupendous Annus Magnus of hundreds of thousands of years, during which the earth's orbit itself breathes in and out in response to the attraction of the planets. But these periodic phenomena, however important they may be to us mere creatures of a day, are insignificant in their effects on the grand evolution through which the celestial bodies are passing. The really potent agents in fashioning the universe are those which, however slow or feeble they may seem to be, are still incessant in their action. The effect which a cause shall be competent to produce depends not alone upon the intensity of that cause, but also upon the time during which it has been in operation. From the phenomena of geology, as well as from those of astronomy, we know that this earth and the system to which it belongs has endured for ages, not to be counted by scores of thousands of years, or, as Prof. Tyndall has so well remarked, “Not for six thousand years, nor for sixty thousand years, nor six hundred thousand years, but for æons of untold millions.” Those slender agents which have devoted themselves unceasingly to the accomplishment of a single task may in this long lapse of time have accomplished results of stupendous magnitude. In famed stalactite caverns we are shown a colossal figure of crystal extending from floor to roof, and the formation of that column is accounted for when we see a tiny drop falling from the roof above to the floor beneath. A lifetime may not suffice for that falling drop to add an appreciable increase to the stalactite down which it trickles, or to the growing stalagmite on which it falls; but when the operation has been in progress for immense ages, it is capable of the formation of the stately column. Here we have an illustration of an influence which, though apparently trivial, acquires colossal significance when adequate time is afforded. It is phenomena of this kind which the student of nature should most narrowly watch, for they are the real architects of the universe.

The tidal consequences which we have already demonstrated are emphatically of this non-periodic class—the day is always lengthening, the moon is always retreating. To-day is longer than yesterday; to-morrow will be longer than to-day. It cannot be said that the change is a great one; it is indeed too small to be appreciable even by our most delicate observations. In one thousand years the alteration in the length of a day is only a small fraction of a second; but what may be a very small matter in one thousand years can become a very large one in many millions of years. Thus it is that when we stretch our view through immense vistas of time past, or when we look forward through immeasurable ages of time to come, the alteration in the length of the day will assume the most startling proportions, and involve the most momentous consequences.